Tout d’abord, dès le séminaire de fin d’année de l’IREM en juin 2020, une présentation des jeux Sowing (inventé par Conway) et Nim (étudié par Conway) a été donnée :
Le séminaire de rentrée de l’IREM s’étant déroulé en distanciel, ce fut l’occasion de montrer une partie commentée du jeu phutball afin d’introduire les principes de ce jeu, créé par Conway et apparemment son jeu préféré. Une rubrique phutball devrait être créée dans CultureMath, mais cela n’a pu se faire durant l’année scolaire 2020-2021. Voici les premières contributions qui lui étaient destinées :
| règle du jeu | exemple de Conway | énigme pour débutants |
|
|
|
Le séminaire du 7 octobre a été l’occasion de présenter le problème de l’ange avec une introduction à la programmation objet.
| La présentation en HTML | Les divers scripts |
|
|
Attention, Le KingBlocker est encore buggué.
Le séminaire du 4 novembre a été l’occasion, via une présentation de la théorie des codes correcteurs d’erreur, d’évoquer les groupes sporadiques et la contribution de Conway à ce sujet :
La fête de la science a permis de présenter
- le cercle de Conway et sa généralisation (David Pouvreau)
| l’article Quadrature | cercle de Conway | Cercle de Pouvreau |
|
|
|
|
- la suite de Collatz et des illustrations musicales (Ivan Riou)
L’article d’Ivan sera disponible ultérieurement sur cette page.
Le séminaire du 2 décembre a été l’occasion de présenter les soldats de Conway. Il s’agit d’une variante du jeu de solitaire où il est surprenamment difficile de propager loin du départ, un des pions.
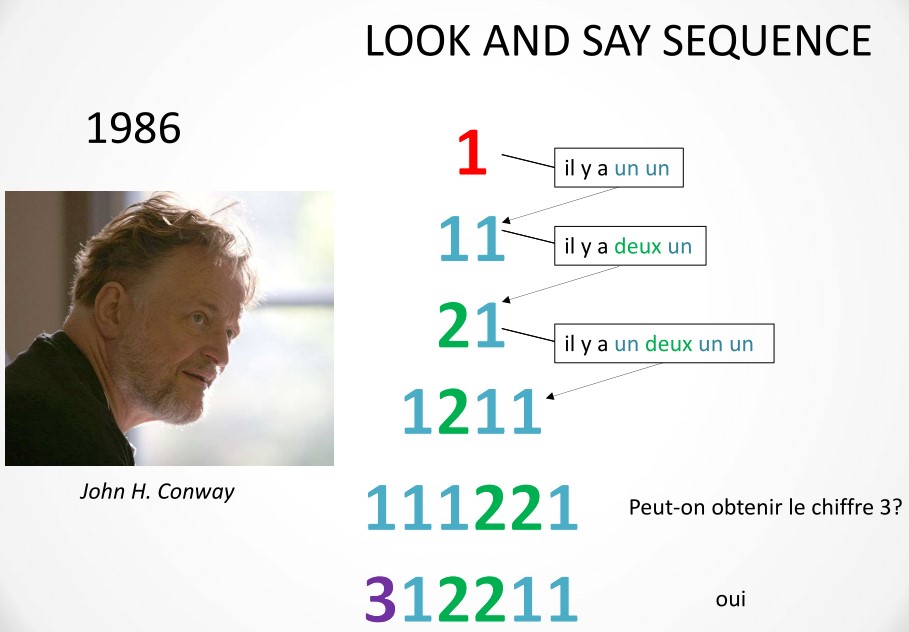
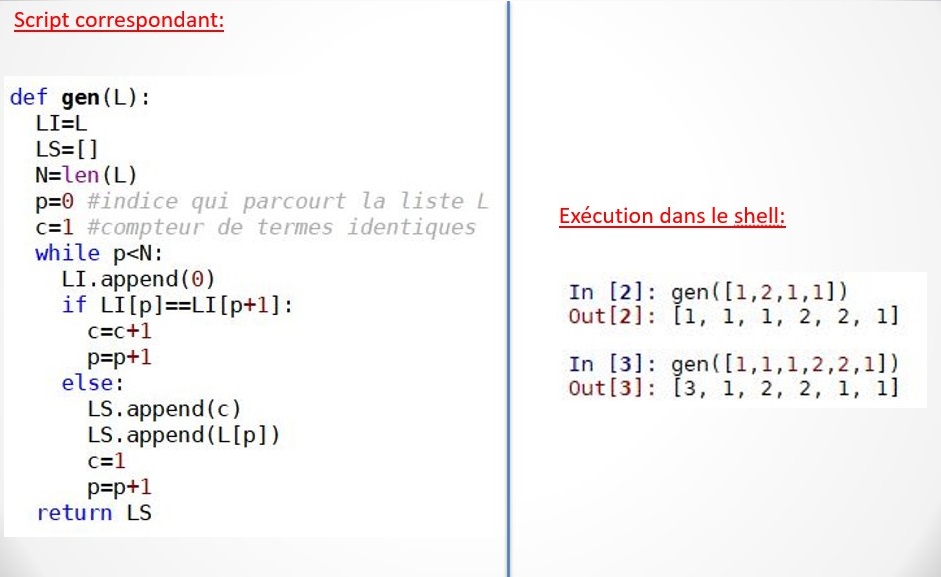
Le séminaire du 3 février a été consacré, entre autres, à la suite de Conway présentée en première professionnelle avec des listes Python. En voici un succinct résumé de la façon dont cette suite a été présentée aux élèves :
Situation déclenchante
En 1992, dans son livre « Le jour des fourmis », Bernard Werber propose comme énigme de compléter la suite ci-dessous :
Quelques années auparavant, Conway avait proposé sa suite « audio-active » (« look and say sequence » en VO) :
Les scripts produits lors de ces activités sont fournis ci-dessous :
D’autres exemples peuvent être vus ici
Mais le même jour, a été présentée l’approche « objet » du langage de programmation Sofus, avec une introduction (pour expliquer le nom de Sofus) à la théorie des groupes de Lie. Or le groupe des rotations en dimension 8, dont le système de racines est D4, a été étudié par Conway :
Le séminaire du 3 mars a été l’occasion de présenter les travaux de Conway sur la suite de Collatz et notamment la création par Conway du langage de programmation Fractran :
Conway n’a pas été évoqué lors de la semaine des mathématiques, celle-ci étant très largement consacrée aux 20 ans de l’IREM.
Mais lors du séminaire de fin d’année, à propos des programmes de NSI et de MPII, a été évoqué l’algorithme de Conway :
Voici des machines dont le look a été inspiré par Conway (boutons et LEDs) pour tester les automates qu’elles représentent :
| l’automate de la présentation | automate de divisibilité par 3 | automate de divisibilité par 5 |
|
|
|
|
Commentaires