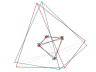
Le tétraèdre est son propre dual :
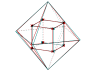
Le dual du cube est un octaèdre :
... et le dual d’un octaèdre régulier est un cube :
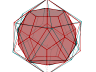
Le dual d’un dodécaèdre est un icosaèdre :
... et le dual d’un icosaèdre est un dodécaèdre :

5 polyèdres réguliers, donc 5 anaglyphes...
En cliquant sur un des petits anaglyphes ci-dessous, on télécharge une figure zir à ouvrir dans CaRMetal
Le tétraèdre est son propre dual :
Le dual du cube est un octaèdre :
... et le dual d’un octaèdre régulier est un cube :
Le dual d’un dodécaèdre est un icosaèdre :
... et le dual d’un icosaèdre est un dodécaèdre :
Forum Ma(th)nipulez !
Mercredi 10 mai 2023, 13 h-17h30, Collège Henri Matisse, Saint-Pierre
L’IREM de Limoges a réussi à inscrire au P.A.F. une journée de présentation de DGPad ; la tortue y a eu un franc succès. Voici le compte-rendu. Il y a des ressources à réinvestir en classe, n’hésitez pas à y puiser !
La révolution tactile, toute naissante, en est probablement à ses premiers balbutiements. Et pourtant, ses premières réalisations contiennent déjà de petits bijoux. C’est le cas, pour ce qui est de la géométrie dynamique, de DGPad. En deux articles sur MathémaTICE, Yves Martin propose un vaste tour d’horizon de cette nouvelle application.
Myriam Bouloc Rossato et Jean-Jacques Dahan ont conçu un scénario interactif pour enseigner les notions de périmètre, d’aire et de volume au collège à l’aide de la géométrie dynamique (Cabri 2Plus et Cabri 3D). Le document s’appuie sur des figures animables en ligne et sur des vidéos postées sur YouTube.
Notre collègue Jean-Louis Ayme est à l’honneur : il vient de publier un nouveau théorème, le « théorème d’Ayme » ou « théorème des quatre points ».
Deux nouveaux points remarquables du triangle, les points X3610 et X3611, lui ont été attribués - ainsi qu’à Peter Moses - par Clark Kimberling dans son Encyclopedia of Triangle Centers.
Geometry Géométrie Geometria est un site extrêmement riche réalisé par Jean-Louis Ayme : entièrement consacré à la géométrie du triangle, il mérite d’être visité longuement.
On pourra lire notamment le très attrayant volume 20 sur les cercles inscrits égaux, qui fait écho à des articles déjà publiés sur le site de l’IREM.


Commentaires