Qu’est-ce que l’idéal ?

Pour une fois ne nous précipitons pas sur le dictionnaire. Consultons une autre source, la poésie. Il paraît en effet que les poètes, surtout les poètes maudits, les pauvres poètes, les poètes mendiants, ceux qui se pendent aux réverbères ou ne trouvent jamais leur place dans la société en savent long sur le sujet. Voici une œuvre qui évoque précisément l’idéal.

Ce sonnet évoque en même temps que l’errance du poète, sa misère et sa grandeur. Sa grandeur dans sa misère. Mais, pour nous aujourd’hui, fêtant la semaine des mathématiques sur le thème « Les mathématiques nous transportent », il peut évoquer aussi bien la pensée mathématique que la poésie ! Il désigne aussi bien le poète que le mathématicien ! Le poème ne décrit pas la fugue d’un adolescent ou le parcours d’un trimardeur, bohémien ou SDF. Il ne décrit même rien, mais suggère un état d’errance, de flottement.

En relisant attentivement son premier quatrain, quelles caractéristiques apparaissent ? « Je m’en allais (...) » ; le premier vers parle d’un cheminement vers on ne sait où dans un état de dénuement. Une démarche libre.

Le second vers évoque une chose, un manteau, « paletot », être matériel qui devient « idéal », qui tend à disparaître matériellement, s’effiloche, mais demeure au moins comme forme ou comme souvenir. Cet être est un être idéal, une idéalité, être qui ne peut pas disparaître pour la pensée, puisqu’il se conserve comme éternellement identique à lui-même !

Le troisième vers reconnaît une qualité rare et précieuse, avec le nom « Muse », mot d’origine grecque qui renvoie à une sorte d’être divin, de personnage mystérieux ou invisible — elle aussi absente du monde et néanmoins présente à lui — une puissance divine : une puissance d’inspiration. Le « féal » de la Muse, lié à elle, possède grâce à elle une capacité à saisir la vérité. Il atteint une sorte de vérité qui échappe naturellement à l’appréhension, une vérité qui, de fait, ne correspond pas aux opinions dont se gave le commun des mortels.

Avec son « Oh ! là là », le quatrième s’amuse de l’abondance des rêves, ces productions de l’imaginaire, toutes ces idées intuitives, qui viennent on ne sait pourquoi à l’esprit, qui découlent de ce cheminement, participent de l’idéal, sous un ciel capable d’inspirer les âmes nobles.

Reprenons les points soulevés. Nous n’avons peut-être pas eu tort de penser aux mathématiques si le poème évoque non une vulgaire promenade, mais un cheminement personnel, au sens d’engagement dans une aventure. Comme un cheminement de la pensée, la pensée mathématique serait à rapprocher :

• d’une sorte de démarche libre, on sait d’où on part, on ne sait pas où l’on va aboutir ;
• d’un trajet solitaire, mais pas forcément dans la solitude absolue ;
• d’un voyage initiatique, faisant droit à l’imaginaire ;
• d’une façon de passer d’un monde à un autre monde, de se détacher de certaines impressions immédiates et de se fier à quelques intuitions fécondes !

Certes, il ne sert à rien de forcer les rapprochements. L’analogie, pour le philosophe plus encore que pour les autres hommes, est une tentation et parfois un piège terrible. Pour cette leçon, nous partirons non de certitudes, mais d’une simple hypothèse : les mathématiques pourraient être un cheminement sous les étoiles. Un dépouillement. Une quête de l’idéal, dans un état d’éveil qui n’est peut-être pas très éloigné de la condition bohème du poète rimbaldien.

Laissons maintenant le poème vivre sa vie en nous. Apprenons-le par cœur ! Et voyons plus précisément le rapport à l’idéal qu’entretient le mathématicien dans sa pratique, dans sa recherche.

Quelques illustrations de l’idéal mathématique

Fragment des Éléments d’Eukleidês (Εὐκλείδης) découvert à Oxyrhynque (vers 100 av. J.-C.)

Les Éléments d’Euclide, premier livre dans une version imprimée, preuve du théorème de Pythagore

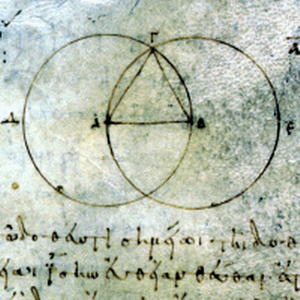
Problème : Sur une droite donnée et finie, construire un triangle équilatéral. Soit AB la droite donnée et finie : il faut construire sur la droite AB un triangle équilatéral. Du centre A et avec un intervalle AB, décrivez la circonférence BCD (demande 3) ; ensuite du centre B et avec l’intervalle BA décrivez la circonférence ACE, et du point C, où les circonférences se coupent mutuellement, conduisez aux points A, B, les droites CA, CB (demande 1). Car puisque le point A est le centre du cercle CDB, la droite AC sera égale à la droite AB (définition 15) ; de plus, puisque le point B est le centre du cercle CAE, la droite BC sera égale à la droite BA ; mais il a été démontré que la droite CA était égale à la droite AB : donc chacune des droites CA, CB est égale à la droite AB ; or les quantités qui sont égales à une même quantité sont égales entre elles (axiome 1) ; donc la droite CA est égale à la droite CB : donc les trois droites CA, AB, BC sont égales entre elles. Donc le triangle ABC (définition 24) est équilatéral, et de plus il est construit sur la ligne donnée et finie AB ; ce qu’il fallait faire. Sources : Sites Remacle et Apmep.

De quelle manière les mathématiques procèdent-elles de l’idéal ? De quelle manière s’y élèvent-elles et peuvent-elles redescendre des sommets atteints ? Pour le comprendre une seule chose est nécessaire : il convient de réfléchir non à ce quoi pense le mathématicien en faisant abstraction de ce qu’il fait, mais à ce qu’il fait pour aboutir à ce qu’il pense. À quelles activités (concrètes ou non) se livrent les mathématiciens pour aboutir à de telles œuvres ?

N. B. Une affirmation si lourde de sens que « une seule chose est nécessaire » ne renvoie à aucune évidence, mais dénote l’adoption d’une perspective épistémologique. D’autres conférenciers pourraient ne pas y souscrire, parce qu’ils ont adoptés une autre perspective. J’assume totalement la mienne, que je crois être la meilleure ! Ce n’est pas seulement la mienne, mais une perspective que j’ai découverte chez des auteurs, de grands penseurs, qui concerne l’idée qu’on doit se faire de la science en général. Elle s’éclairera dans la suite, par son application au cas des mathématiques. Son principe est de ne pas survaloriser les discours au détriment des pratiques, du faire, de l’engagement dans des projets concrets. Les discours prennent sens dans un contexte pratique déterminé. Pragmatisme.

Les mathématiques, un ensemble d’opérations symboliques

Que faisons-nous ordinairement quand nous agissons (quand nous nous amusons, quand nous travaillons, quand nous utilisons une machine qui travaille à notre place...) ? Toute activité est l’obtention de résultats déterminés à partir de moyens mobilisés. Quand je fais une tarte Tatin, je me livre à une série d’opérations concrètes : peler des pommes, les couper, caraméliser du sucre au fond d’un moule, mélanger de la farine et du beurre, étendre la pâte au rouleau, poser les pommes sur le caramel, déposer la pâte sur les pommes... Tout cela a un ordre et il y a des incompatibilités. Ordre : je ne pose pas les pommes sur le caramel avant d’avoir obtenu le caramel (même si je peux par fainéantise déposer les pommes sans les avoir épluchées). Respect du faisable : je ne peux éplucher les pommes et mélanger les ingrédients en même temps, si je n’ai que deux mains... Nul ne niera donc qu’il y a une logique dans l’activité pâtissière.

Et c’est la même logique à une nuance près qu’on retrouve dans la logique des mathématiciens qui construisent des figures, comparent des nombres, résolvent des équations, etc. Cette nuance est assurément la suivante : la logique des mathématiques est une logique idéale, purement symbolique, puisque les opérations effectuées sont non pas matérielles, mais symboliques, c’est-à-dire représentées par des signes et portées par eux seuls. Un cuisinier produit une tarte, pas une recette ou une idée de tarte ; un mathématicien produit une idée d’angle droit, pas une équerre en bois ou en plastique. L’angle droit du mathématicien, qui n’est pas même ce qu’il peut dessiner au tableau mais ce qu’il vise en le faisant, ne s’incarne jamais autrement que dans une écriture 90° ; π/2 ; ∟ ; ou par la grâce d’un symbole arbitraire, qui n’est pas forcément une copie du réel !

Les symboles ne viennent pas de nulle part. Ils sont les signes (arbitraires) de diverses opérations géométriques dérivant d’opérations concrètes. Par exemple plier une feuille puis replier le pli en deux. Et si l’on peut dire un angle par un nombre, c’est qu’on a adopté une mesure, un moyen de mesurer (une métrique), qu’on juge appropriée ou simplement pratique. Pourquoi dire 90° ? Parce qu’on possède un rapporteur gradué avec cette unité de mesure des degrés d’angles. Les opérations auxquelles se livrent les mathématiciens sont des « opérations possibles, indiquées par des symboles et accomplies uniquement par le moyen de symboles » (p. 174).

Tous les scientifiques utilisent également des symboles, une écriture symbolique, dans la partie théorique de leurs recherches, comme le chimiste qui étudiant le glucose, se réfère à C₆H₁₂O₆. Ce faisant il dépasse la prise en compte des qualités sensibles pour établir des réactions chimiques ayant leur logique propre, leur bilan énergétique, sous couvert de conservation de la matière, c’est-à-dire des différents éléments chimiques représentés par les lettres C, H ou O.

Est-ce donc la même chose ? Pas vraiment. Contrairement aux chimistes, les mathématiciens associent des symboles d’opérations possibles sans tenir compte de réalisation effective. Ils poussent, comme on dit, l’abstraction plus loin. Les 6 et 12 de C₆H₁₂O₆ désignent des opérations applicables à toute molécule de glucose : par analyse, la production de six atomes de carbone, de douze atomes d’hydrogène et de six atomes d’oxygène, à partir d’une seule molécule. Les nombres du mathématicien n’indiquent en revanche aucune opération applicable à quoi que ce soit de déterminé... ou, si l’on préfère le dire positivement, ils « désignent une opération applicable à toute chose quelle qu’elle soit » (p. 175), chose restant indéterminée. Cet objet est paradoxalement conçu dans l’abstraction de l’effectivité de la réalisation de toute opération particulière.

Le 6 du mathématicien n’a aucune qualité particulière, Ni le 12. Aucune ! Vraiment ? Ce sont des nombres pairs... donc ils conserveraient une qualité particulière, au moins. Faisons attention à ne pas jouer sur les mots. Le mathématicien ne prend véritablement en compte rien comme une distinction qualitative... contrairement à l’élève qui obtenant 6 comme note à son contrôle de philosophie soupire et regrette le 20 dont il rêvait, pensant que s’il avait eu 12 l’honneur aurait été sauf. Il n’en tient pas compte, car il n’en a pas besoin. Les entiers entretiennent avec tous les autres nombres des relations définies. D’où leur parité, ou non ! S’ils entretiennent ces relations de manière nécessaire c’est précisément dans le cadre de la construction des idées et le maniement des symboles, rapporté à des opérations possibles, qui font abstraction de l’effectivité de leur réalisation. Le 6 du mathématicien n’est pas « peu », contrairement au 6 note de l’élève, ni beaucoup. Ce 6 comme nombre diffère même du 6 comme « nombre de », par exemple nombre de bonbons à distribuer à des enfants pour que chacun soit content... situation concrète pour laquelle la parité importe qualitativement, comme expression de la justice distributive.

Ce 6 sans qualité n’est donc ni une essence (le 6 qualitatif, nombre suprême du dé, ou l’Idée du six, la sizaine idéale), ni une propriété de choses existantes (les six bonbons pour les enfants), mais une simple « désignation d’opérations potentielles » (p. 176) ! Et ce qui est valable du 6 ou de tout entier est valable de tout autre objet, même plus compliqué en apparence. Les autres nombres, les calculs, les solides, les fonctions, les classes, les fractales, les curvicas, les nœuds... Par exemple, l’espace mathématique :

« L’espace mathématique n’est pas un genre d’espace distinct du prétendu espace physique et empirique, mais c’est un nom donné à un ensemble d’opérations idéalement ou formellement possibles concernant des choses ayant des qualités spatiales : ce n’est pas un mode d’Être mais une manière de penser les choses qui rend possibles, entre ces dernières, des rapports d’implication et libère les connexions entre elles de la fixité qui est la leur dans l’expérience. » (p. 176)

L’espace mathématique est une idée. Une idée n’est pas quelque chose qui existe d’une existence indépendante de moi, mais quelque chose qui participe de mon jugement et des opérations qu’abstraitement j’imagine. Et « Toute idée en tant que telle désigne non pas quelque chose qui possède une existence effective, mais une opération qui pourrait être accomplie. » L’idée de la douceur du caramel de la tarte Tatin... Pas la qualité sensible en tant qu’elle est éprouvée, hic et nunc. D’ailleurs, ici et maintenant, il n’y a pas de parts de tarte à goûter... mais l’idée de la douceur s’impose à moi, en tant qu’indication de ce qui se passerait si je pouvais goûter un morceau de tarte. L’idée d’espace mathématique est de même pensé, imaginé, supputé, visé dans l’abstraction de toute chose.

Essayons de penser à d’autres tartes absentes de toute table (allusion à la fleur de Mallarmé « absente de tout bouquet »), tarte à ceci ou à cela... il y aura bien quelqu’un pour penser à une horreur, la tarte non plus sucrée mais salée, ou la tarte sans beurre (avec du saindoux)... la tarte sans ceci ou avec cela... D’ailleurs la tarte Tatin était déjà, si on pense, une monstruosité puisque renversée ! De même qu’il n’y a pas qu’une tarte il n’y a pas qu’un espace. En plus de l’espace euclidien, des espaces monstrueux existent, non euclidiens. Comme il existe des tartes non sucrées mais salées. Et aucun n’est plus normal qu’un autre. Dire qu’une tarte Tatin est renversée, c’est relatif. Une tarte ordinaire est d’un point de vue logique une tarte non non renversée... Les espaces mathématiques ne sont pas qualitativement monstrueux, car ils n’ont aucune caractéristique qualitative. Pas même la qualité de bien représenter l’espace physique ou ce qu’on croit désigner par là !

Il y a possibilité et (com)possibilité

Nous avons franchi une étape décisive dans la compréhension de l’objectivité mathématique en pensant l’objet dans sa dimension symbolique et en traduisant celle-ci comme pensée libre d’opérations possibles, non effectives, non appliquées à quoi que ce soit de particulier. Que veut dire « possible » (ou potentiel, les deux mots ayant globalement le même sens) ? La menace de voir la compréhension s’éloigner au moment même où nous nous rapprochons du but doit nous conduire à un premier approfondissement...

« Possible » dans le langage ordinaire renvoie souvent à une action passée en tant qu’elle pourrait se reproduire, bientôt, comme ne pas se reproduire de sitôt, dans le cas où le possible est fort peu probable. Par exemple, il est possible que je perde 1 point sur mon permis de conduire en rentrant à Saint-Denis, même si je conduis prudemment en général. C’est possible, car j’ai déjà perdu 1 point lors d’un contrôle radar de vitesse... C’est possible aussi puisque que d’autres que moi ont déjà été flashés. Pourquoi pas moi à mon tour ? Cette possibilité demeure existentielle, aussi peu probable soit-elle.

Mais ce n’est pas le type de la possibilité à laquelle nous nous référons en disant que le nombre 2 ou l’espace sont des désignations pour des opérations strictement possibles et pas effectives. C’est bien un sens secondaire du mot, quand on n’envisage plus ni le passé ni l’avenir, mais seulement la possibilité d’opérations logiques les unes par rapport aux autres ! Opérations logiques et pas chronologiques. En ce sens second, un peu étrange, il est possible que je perde 1 point sur mon permis de conduire à points seulement parce qu’il m’en reste, parce qu’il m’en reste à perdre. Si je les avais déjà tous perdus, cela ne serait plus possible !

La possibilité à laquelle nous devons penser pour saisir l’objectivité spéciale des objets mathématiques compris comme objets sur lesquels peuvent porter des opérations symboliques est donc, doit-on dire pour être plus rigoureux, une compossibilité d’opérations visées. Un seul test existe pour établir une compossibilité d’opérations, c’est leur non incompatibilité. Ordinairement on parle de cohérence... mais il s’agit ici du fait que les énoncés sont non contradictoires et donc respectent la consistance du système formel.

Dans notre vie quotidienne la règle de la compossibilité vaut également. Par exemple, si l’on songe à quelqu’un qui gère un budget, il peut employer tout son capital pour acheter une voiture neuve ou pour investir dans la bourse. Mais il ne peut employer le capital pour l’achat de la voiture et l’achat d’actions en bourse. Ou encore, en droit français, il est possible de se marier avec quelqu’un si l’on a l’âge requis pour se marier, mais aussi si l’on n’est pas déjà marié et si la personne avec qui on veut se marier n’est pas déjà mariée.

Dans l’ensemble du domaine des mathématiques, la non incompatibilité est la seule règle qui vaille. Pas en économie ou en droit, où d’autres règles vont être suivies par les acteurs économiques et par les acteurs juridiques, les règles qui indiquent ce qu’il importe de faire pour satisfaire un intérêt particulier (pathologique). Règles de la prudence, de la nécessité conditionnelle. La non incompatibilité n’est pas la règle décisive, elle apparaît même si évidente qu’elle peut n’être pas reconnue comme telle ! On ne se marie pas avec n’importe qui ; on ne dépense pas son argent n’importe comment quand on en a... Mais quelques artifices légaux ou formes d’échange peuvent nous amener à restaurer la non incompatibilité comme règle décisive, et peut-être même arriver à penser ce qu’est un monde dans lequel régnerait, seule, la règle de la non incompatibilité. Comme règle absolue.

Premier exemple déroutant. Sur les marchés financiers, il est possible d’acheter certains titres pour des sommes bien supérieures, dix fois supérieures par exemple, à son capital de départ. J’ai 100 euros et j’achète pour 1000 euros de titres sans emprunter ! C’est ce que permet la technique du bras de levier sur des marchés échangeant par exemple des produits dérivés... mes 100 euros n’étant pas considérés comme mon avoir, mais comme ce que je mise et suis prêt à perdre lors de la transaction.

Deuxième exemple déroutant. En droit du mariage il peut être possible de se marier avec une personne morte. C’est le cas de femmes qui étant fiancées à un soldat tué au combat peuvent obtenir un mariage posthume et faire reconnaître un enfant « obtenu » lors d’une permission. Ce que ce dernier cas nous apprend, c’est l’existence d’une autre compossibilité que la compossibilité ordinaire, suivant laquelle il n’est ordinairement possible de se marier qu’avec une personne en vie.

Article 171 du Code civil :
« Le Président de la République peut, pour des motifs graves, autoriser la célébration du mariage en cas de décès de l’un des futurs époux, dès lors qu’une réunion suffisante de faits établit sans équivoque son consentement.
Dans ce cas, les effets du mariage remontent à la date du jour précédant celui du décès de l’époux.
Toutefois, ce mariage n’entraîne aucun droit de succession ab intestat au profit de l’époux survivant et aucun régime matrimonial n’est réputé avoir existé entre les époux. »

Après avoir pensé la possibilité d’utiliser l’argent sur les marchés, bien des subtilités de la pratique du crédit pourraient être évoquées ; après avoir pensé la possibilité d’un mariage avec une personne décédée, bien des contrats civils, pacs, mariages entre personnes du même sexe, mariages temporaires, etc. pourraient être évoqués.
Il s’agit de possibilités monstrueuses qui peuvent nier la valeur de l’argent, à mes yeux, ou m’apparaître comme contraire à l’essence du mariage... parce que je fais fonctionner, sans m’en rendre compte, des déterminations qualitatives et subjectives. Pourquoi pas, demain, de l’argent à date de péremption ou des mariages de groupes ? Qu’est-ce que le monstrueux dans l’ordre de réalité dont on parle, les réalités socialement construites ? N’est-ce pas, comme en mathématiques, un jugement dont on peut se passer ?

Le possible déborde en quelque sorte ce que je crois possible à un instant t. Dans l’apprentissage des mathématiques, l’écolier apprend d’abord qu’il est possible de faire l’opération suivante 12 – 7 mais qu’on ne peut pas faire l’opération 7 – 12. Puis au collège, il apprend que c’est possible. Que c’est possible et que cela veut dire quelque chose alors que cela semble incohérent ! Remontons le cours du temps et des apprentissages. L’écolier a d’abord appris à faire des opérations notées +, des opérations additives. Et il est passé à des opérations notées –, opérations soustractives. Pour obtenir le bon résultat, il a d’abord été habitué à résoudre des problèmes comme « combien faut-il ajouter à 7 pour avoir 12 ? ». C’est donc à une première reconnaissance d’opérations différentes mais équivalentes qu’il a été confrontée (sans avoir toutefois conscience de cela) et maintenant avec 7 – 12 c’est à une nouvelle possibilité équivalente qu’il est confronté. Possibilité d’une opération notée –, résistant au test de la non incompatibilité dans l’ensemble des nombres relatifs, et voulant dire + (–12).

Nous avons au passage oublié quelques étapes qu’il est possible de juger décisives. En apprenant à faire des opérations notées + et opérations notées –, à manier des nombres positifs ou négatifs, l’enfant a pu être désarçonné. Est-ce que – et – dans –12 c’est pareil ? En revanche il n’a sans doute pas été désarçonné par autre chose, bien qu’il ait été confronté à de très étranges opérations possibles. Comme celles-ci : 7 + 0 ou bien encore 7 – 7. Opérations pour lui rendues possibles par le langage mathématique qu’on lui a fait apprendre très jeune, mais qui seraient restées impossibles à un écolier romain ou grec ! 7 + 0... on peut toujours dire qu’on ajoute rien et donc qu’il n’ y a pas d’addition... ou dire, avec 7 – 7, qu’on a plus rien quand on a tout enlevé. Mais cela n’a pas de sens que de produire l’énoncé 7 + rien ou 7 – 7 = rien. Ce qui se joue dans l’adoption du symbole 0 comme nombre est une compréhension élargie de ce qu’est un nombre. Compréhension de ce que peut être un nombre, à partir du moment où on reconnaît qu’un nombre n’est pas une quantité mais une idée, qu’un nombre est sans qualité car c’est l’indication d’une pure potentialité opérative.

Entre art et industrie, les mathématiques en voie de développement

« La non incompatibilité indique que tous les développements sont les bienvenus pour autant qu’ils n’entrent pas en conflit les uns avec les autres ou aussi longtemps que la reformulation d’une opération prévient tout conflit effectif. C’est un canon de libération plus que de restriction. On peut le comparer à la sélection naturelle, qui correspond à un principe d’élimination, mais non à un principe exerçant un contrôle sur le développement positif. » (p. 176)

Cela marche si l’on reprend nos exemples triviaux. « Tous les développements sont les bienvenus » : 7 – 12 ? pourquoi pas ! « aussi longtemps que la reformulation d’une opération prévient tout conflit effectif » : 7 – 7 ? cela veut dire « combien faut-il ajouter à 7 pour avoir 7 ? », 0 car 7 + 0 = 0 !

Et l’on peut même assez facilement accepter l’idée qu’il s’agisse d’un canon – i. e. une règle – de libération plus que de restriction. Des restrictions pourront être découvertes... par exemple, malgré la possibilité de l’opération 7 x 0, l’impossibilité de l’opération 7 / 0. Mais ces restrictions n’indiquant que des incompatibilités, le surgissement d’une incohérence, ne sont pas des limitations cognitives, des barrières pour l’esprit. Et le développement des mathématiques repose sur une libération de l’imagination permise par la nature purement symbolique des opérations visées...

Maintenant pour bien comprendre la comparaison des mathématiques en développement avec le développement du vivant... et donc comprendre à cette occasion que les mathématiques sont vivantes !... il faudrait connaître ce qu’est la sélection naturelle, avec Darwin bien sûr, et ce qu’elle n’est pas. Si tout le monde a entendu parler de cette théorie, force est de reconnaître que tout le monde ne maîtrise pas ce qu’elle signifie. L’idée essentielle de la théorie biologique est sans doute contre-intuitive : le vivant connaît un développement qui n’est pas orienté. La théorie de la sélection naturelle fait abstraction de toute finalité, de tout but à atteindre. C’est pourquoi on peut dire que Darwin explique la diversité du vivant et l’adaptation au milieu des organismes par un principe d’élimination aveugle et pas un principe de création en vue d’une fin donnée. La nature n’a pas créé les yeux pour que les animaux puissent voir, aussi incroyable que cela puisse paraître ! De même, elle n’aurait pas inventé les nombres naturels pour que les hommes puissent compter et devenir des capitalistes... elle n’aurait pas créé les figures et l’espace euclidien pour que les peuples puissent procéder à des opérations d’arpentage et bientôt établir un cadastre...

Généré par douze mots de notre langue usuelle « naissance si trois cellules voisines, survie si deux ou trois cellules voisines », l’automate cellulaire du « jeu de la vie » de John Horton Conway permet aujourd’hui de visualiser ce que veut dire l’affirmation suivant laquelle la non incompatibilité est un « canon de libération » dans un monde idéal. Monde déterministe exemplaire, « démocritéen », en l’espèce, pour reprendre l’expression d’un philosophe contemporain, Quine. Ce qui se crée au jeu de la vie (une grenouille, une tête de clown, un canon à planeurs, une chute de bombes non périodique, un jardin d’Eden...) ne correspond à aucun plan préétabli. Les formes « vivantes » qui se développent sont le pur produit des règles de base du jeu. Or, participant de la même logique combinatoire, produisant des êtres calculables mais déjouant la calculabilité a priori, le développement des mathématiques peut être considéré comme similaire au développement des formes de vie du jeu de la vie !

De manière générale il est donc permis de douter de la création des mathématiques en dehors du monde ou avant lui, par Dieu – sive natura – la Nature, une quelconque puissance transcendante. Hypothèses dont on n’a pas besoin. Et donc il est raisonnable de ne pas tenir les objets mathématiques pour des êtres divins qui entreraient, de près ou de loin, dans la réalisation d’un Plan divin. Est-ce qu’il n’entre toutefois aucune finalité dans la fabrique des idéalités mathématiques ?

Après la comparaison avec le développement du vivant qui s’opère sans principe vital transcendant, deux autres rapprochements sont nécessaires pour éclairer l’idée de fécondité. Les voici :

« Les mathématiques et la logique formelle correspondent ainsi à des branches hautement spécialisées de l’industrie intellectuelle. Les principes qui y sont à l’œuvre sont très similaires à ceux qui opèrent dans le domaine des beaux-arts. Le trait qui de manière frappante les caractérise est une combinaison de liberté et de rigueur – liberté pour ce qui est du développement de nouvelles opérations et idées, rigueur s’agissant des compossibilités formelles. La combinaison de ces qualités qui définit aussi les grandes œuvres d’art exerce sur certains esprits une grande fascination. Mais la croyance selon laquelle ces qualifications soustrairaient les objets mathématiques à toute connexion avec l’existence est l’expression d’une disposition religieuse plus qu’une découverte scientifique. » (p. 177)

Comparaison avec l’industrie. Le développement des mathématiques est en un sens mécanique. Et il est possible de parler d’industrie pour désigner la machine qui produit aujourd’hui en masse les résultats mathématiques, de nouveaux théorèmes. La machine, sans être péjoratif, ou le corps des mathématiciens spécialisés, souvent universitaires, qui appliquent rigoureusement, dans leur tête et sur le papier, les règles établies de formation des énoncés et les règles de transformation de ces énoncés.

Comparaison avec l’activité artistique. Ce développement des mathématiques est aussi artistique, et en cela aussi imprévisible que les courants esthétiques qui émergent à partir d’œuvres de quelques précurseurs. Et là, tout est « possible » en accentuant l’admiration ou l’effroi... il s’agit de penser la possibilité de l’invention au sens courant du terme, la découverte ou redécouverte de voies de résolution de problèmes. Il n’est pas si rare qu’un mathématicien invente dans son coin ce qui avait été établi ailleurs et dans une autre époque.

Les théorèmes mathématiques sont-ils découverts ou inventés ? La question est classique. La réponse n’est pas si aisée.

Dépasser le platonisme ?

Dire que les objets mathématiques sont de pures inventions, des créations de l’esprit humain et qu’ils n’existent pas indépendamment des esprits qui les pensent, qui les ont inventés ou réinventés, ce n’est pas les dénigrer. Ce n’est pas les affaiblir non plus ! Nombres et figures n’ont pas d’existence, au sens courant du verbe « exister ». Mais ils n’en existent pas moins à leur manière. Il n’est permis de dire qu’ils « existent » qu’après avoir étendu la signification du verbe exister à ce genre d’existence soutenu par et contenu dans la seule non-incompatibilité.

Dire que les objets mathématiques n’ont pas de signification, puisqu’ils ne se réfèrent à rien en particulier et sont évoqués par des termes dont la valeur est purement arbitraire. Ce n’est pas non plus dénoncer un quelconque manque. Au sens courant du verbe « signifier » ou de l’expression « avoir du sens », les mathématiques ne signifient rien ou n’ont pas de sens. Elles ne sont pas même « vraies », même si on peut les concevoir comme utiles ou efficaces. La signification des objets mathématique est non pas externe, dans une relation à quelque chose d’extérieur, mais interne au système des relations pouvant être établies entre ces divers objets. Aucun arbitraire n’existe, en droit, au sein de ce système de relations ou de transformations symboliques possibles.

Pour ces deux raisons il faut sans doute renoncer définitivement à une ontologie des objets mathématiques. Toutes les comparaisons qu’on pourrait faire, dire par exemple que les figures du géomètre sont comme les ombres d’objets matériels conduisent en fait à une équivoque dangereuse. Le piège étant de confondre l’objet mathématique dénué de réalité existentielle avec quelque chose qui en a, comme le dessin d’un carré ou d’une quelconque figure. Toutes les affirmations métaphysiques qu’on oserait produire sont sans fondement assuré et très certainement illusoires. Par exemple le propos suivant lequel Dieu aurait donné aux hommes les nombres premiers et que les hommes auraient construits tous les autres nombres.

Le platonisme qui cherche à établir dans l’ontologie un statut éminent aux objets mathématiques, élevés au rang d’êtres éternels voire divins, est une position que bien des mathématiciens, et non des moindres, continuent à trouver séduisante. Son ennemi dans l’arène de la métaphysique, la position empiriste, a lui aussi aujourd’hui encore des adeptes. Mais, par delà ces allégeances à des philosophies constituées en dehors des mathématiques, dans l’ignorance partielle ou totale de celles-ci, il convient d’adopter une position raisonnable, qui soit centrée sur l’essentiel.

« La différence significative est celle qui existe entre deux types de possibilité d’opération, matérielle et symbolique. Cette distinction figée comme un dogme, celui des deux ordres de l’Être, de l’existence et de l’essence, fait naître l’idée qu’il y a deux types de logique et deux critères de la vérité, le formel et le matériel, le premier étant plus élevé et plus fondamental que le second. En vérité, le développement formel est un rejeton de la pensée matérielle. Il est ultimement dérivé d’actes accomplis et constitue une extension de tels actes ; des symboles, par les rapports de congruence qu’ils entretiennent, le rendent possible. Il en résulte que la logique formelle représente une analyse d’opérations exclusivement symboliques ; c’est une logique symbolique, en un sens fécond et non externe. Interpréter ainsi les idées mathématiques et logiques (formelles), ce n’est pas les dénigrer, excepté d’un point de vue mystique. Les symboles, comme nous l’avons déjà relevé, sont la seule chose qui nous permet de ne pas être submergés par l’existence. »

« La libération que procure le symbolisme libre des mathématiques est souvent un moyen pour revenir ultérieurement à des opérations existentielles qui ont une portée et une force de pénétration que l’on ne peut atteindre autrement. »

« L’histoire de la physique est riche de cas où des idées mathématiques auxquelles on ne connaissait pas d’application physique ont pourtant suscité de nouvelles relations existentielles. »

Illustrons ces idées, dans l’ordre.

A) D’abord le dogme du platonisme, des deux ordres de l’Être. On passe des deux domaines discursifs, le formel et l’existentiel, à deux régions de l’être, l’essentielle et l’existentielle. L’une élevée, éminente ; l’autre en revanche basse, lourde, mouvante, fausse. Le monde intelligible par opposition au monde sensible. Là où rôde l’accident... On trouve souvent en philosophie ce glissement de sens, de la logique à l’ontologie, chez les penseurs « rationalistes » d’avant le XX^e siècle, tout particulièrement. Chez Descartes, par exemple :

« On voit clairement pourquoi l’arithmétique et la géométrie sont beaucoup plus certaines que les autres sciences : c’est que seules elles traitent d’un objet assez pur et simple pour n’admettre absolument rien que l’expérience ait rendu incertain, et qu’elles consistent tout entières en une suite de conséquences déduites par raisonnement. Elles sont donc les plus faciles et les plus claires de toutes, et leur objet est tel que nous le désirons, puisque, sauf par inattention, il semble impossible à l’homme d’y commettre des erreurs. » (Règles pour la direction de l’esprit, 1628)

Ou Leibniz :

« Les sens, quoique nécessaires pour toutes nos connaissances actuelles, ne sont point suffisants pour nous les donner toutes, puisque les sens ne donnent jamais que des exemples, c’est-à-dire des vérités particulières ou individuelles. Or tous les exemples qui confirment une vérité générale, de quelque nombre qu’ils soient, ne suffisent pas pour établir la nécessité universelle de cette même vérité, car il ne suit point que ce qui est arrivé arrivera de même. [...] D’où il paraît que les vérités nécessaires, telles qu’on les trouve dans les mathématiques pures et particulièrement dans l’arithmétique et dans la géométrie, doivent avoir des principes dont la preuve ne dépende point des exemples ni par conséquence du témoignage des sens, quoique sans les sens on ne se serait jamais avisé d’y penser. » (Nouveaux Essais sur l’entendement humain, 1704)

B) Ensuite, l’antidote au platonisme, point de vue mystique dont il n’est pas si pénible de se déprendre. On établit la liaison de la pensée formelle et de la pensée matérielle, l’une dérivant de l’autre, l’étendant dans la sphère du possible par le biais de symboles. Ce passage présente une difficulté, avec l’emploi du terme de congruence (hors du domaine mathématique où le mot prend un sens particulier) dans un passage qui souligne la puissance propre du symbolisme.

C) L’idée est celle d’un mouvement d’aller et retour. Du réel au théorème et maintenant du théorème au réel. Il ne s’agit pas seulement de dire que le symbolisme de la logique formelle est une prouesse intellectuelle mais de soutenir que celui-ci, quoique formel, parce que formel, est très efficace dans le réel, pour tout le réel ! Comment comprendre cela ? De manière générale, l’usage d’un symbolisme est libérateur pour la pensée. Libérant l’esprit de devoir garder certaines choses en mémoire, les symboles permettent de réaliser plus vite et mieux certaines déductions, certains calculs, certaines démonstrations. L’idée défendue est que les opérations effectuées à l’aide de symboles, dans l’abstrait, gardent un rapport avec les opérations concrètes qui auraient peut-être pu être effectuées, mais précisément en font abstraction pour obtenir virtuellement un résultat. Et un résultat juste.

Exemple, calculer la circonférence d’un cercle de rayon 3 cm. Réponse ? 2πR. 6π...
De manière spéciale, l’usage d’un symbolisme est même très fécond ! Il permet d’obtenir certains résultats autrement impossibles ou très difficile à obtenir...

Exemple, résoudre l’équation suivante, du troisième degré : $x^3 - 6x^2 + 13x - 10 = 0$. Descartes affirme :

« Au reste tant les vraies racines que les fausses ne sont pas toujours réelles ; mais quelquefois seulement imaginaires c’est-à-dire qu’on peut toujours en imaginer autant que j’ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imagine.
Comme encore qu’on en puisse imaginer trois en celle-ci, $x^3 - 6x^2 + 13x - 10 = 0$, il n’y en a toutefois qu’une réelle, qui est 2, et pour les deux autres, quoiqu’on les augmente, ou diminue, ou multiplie en la façon que je viens d’expliquer, on ne saurait les rendre autres qu’imaginaires. » (Géométrie, Livre III, 1637)

D) Il ne faudrait pas oublier les applications des mathématiques à la physique, des sciences formelles aux sciences naturelles en général. Ces applications sont importantes. C’est à leur sujet qu’on parle de l’effectivité des mathématiques. Une manière de passer à côté de l’idée est de répéter comme un mantra que la nature est écrite en langage mathématique, paraphrasant Galilée. Dans l’histoire de la physique, il y a eu plusieurs cas de figure. Soit le physiciens confronté à des difficultés a soudain une sorte de révélation, comprenant tout à coup que le problème qui le faisait transpirer depuis des mois, trouve dans telle expression mathématique qu’il connaissait mais n’avait pas utilisé une voie de résolution à la fois rigoureuse et simple.

Autre cas. Soit le physicien ressent le besoin d’un langage précis, univoque, pour exprimer le problème qui l’intéresse et d’une méthode opératoire pour obtenir des prévisions de résultats. Il parle alors de forces et pense en vecteurs. Il parle de champs et pense des fréquences. Il parle d’états et pense des probabilités. Le cas échéant, il doit alors construire une branche des mathématiques pour pouvoir comprendre les choses physiquement et dégager des lois universelles. C’est le cas de Newton devant construire le calcul intégral pour calculer des aires et pouvoir déterminer des quantités de mouvements... alors que l’idée de la gravitation universelle variant en $1/R^2$ lui a été soufflée par Hooke, formidable penseur et observateur incapable pour sa part d’exprimer mathématiquement de telles relations. D’où le De motu et les Principia mathematica (sur Hooke et Newton, écouter une conférence de Jean-Pierre Romagnan de l’Université de Toulon). On peut multiplier les exemples. C’était avant lui le cas de Descartes perfectionnant la géométrie dans ses recherches sur l’optique. Ce fut après lui le cas de Gauss, inventeur de la méthode des moindres carrés.

Il y a, pour tout dire, d’autres cas, entre les deux premiers. Par exemple le cas du mathématicien qui n’a jamais cessé de se soucier de problèmes de physique et fait en permanence des va-et-vient entre son domaine et le domaine voisin. Poincaré par exemple. Mathématicien obnubilé par le problème des trois corps... la mécanique céleste comme on disait avant. La science qui s’appelle la mécanique, est-ce des maths ou de la physique ? Si vous répondez physique vous êtes comme Matthew Crawford (Éloge du carburateur) un passionné d’engins à moteurs, de bruit pétaradant et de vitesse. Si vous répondez maths, c’est que vous êtes un élève de prépas pestant contre son 6 au dernier devoir et ses calculs infaisables.

L’implication ou la relation idéale des moyens et des fins

Les véritables "objets" mathématiques, qui sont si utiles pour penser des opérations matérielles, ce sont non pas des objets isolés, monadiques, mais des relations entre des objets considérés à dessein comme semblables à eux-mêmes, identiques, dans les divers symboles qui les représentent. Une même essence donnant quantité d’écritures différentes (4 ; 3+1 ; 8/2 ; 22 ; √16 ; 3,999 999. tous ces exemples étant donnés en base 10). Et cette essence n’est pas existante avant la mise en relation des idées, relation logique permettant de réaliser ou non l’identité de ces idées et donc d’unir des écritures différentes par le signe =, en produisant une équation, vraie ou fausse. Comme 4 = 3,999.

« La relation est un invariant. Elle est éternelle, non pas au sens où elle perdurerait de tout temps, ou durerait à l’image d’une espèce aristotélicienne ou d’une substance newtonienne, mais au sens où une opération, en tant que relation appréhendée dans la pensée, est indépendante des instances dans lesquelles elle est ouvertement exemplifiée, bien que l’on ne puisse trouver sa signification que dans la possibilité de ses actualisations. » (p. 179)

Or, loin, d’être monadique, isolé dans un splendide isolement, l’objet mathématique (pyramide, tore, fonction hyperbolique, probabilité, etc.), certes toujours égal à lui-même dans le monde mathématique, correspond à d’infinies possibilités de mises en relation invariantes, idéales, hors temps.

« La pensée d’un objet en tant qu’idéal détermine par conséquent, une structure interne ou une forme caractéristique. Cette structure formelle, les choses existantes ne font que s’en approcher. On pourrait concevoir une machine à vapeur qui soit efficace à 100%, bien que cet idéal ne puisse être le moins du monde atteint effectivement. Ou l’on peut, à l’instar de Helmholtz, concevoir un dispositif optique qui serait dépourvu des défauts qu’on trouve dans l’œil humain tel qu’il est. La relation idéale des moyens aux fins existe comme une possibilité formelle déterminée par la nature du cas envisagée, bien qu’elle ne soit pas pensée et moins encore réalisée, en fait. Elle subsiste comme une possibilité et, en tant que telle, elle est, dans sa structure formelle, nécessaire. » (p. 180)

Si ceci est — tel résultat —, alors cela — tel ensemble déterminé de conditions — est nécessaire ; p implique q ou p → q. Une inférence est possible, un passage de la pensée de p à la pensée de q, une mise en relation de la pensée de p dans son rapport à q. La saisie de l’être relatif de p comme de q.

« La nécessité d’une structure marquée par des relations formelles qui satisfont les conditions attachées au fait de servir de moyens en vue d’une fin rend raison des relations d’implication qui rend la déduction possible » (p. 180)

Pour le raisonnement, dans la vie de tous les jours comme dans les plus hautes spéculations, l’implication est un "instrument" qu’on retrouve partout. Qui est utilisé dans le modus ponens, règle de déduction qui s’énonce ainsi : de p et p → q, on déduit q. Pour le logicien, l’implication (voulant dire « si... alors » ou « seulement si ») renvoie aux opérateurs essentiels, aux opérations de négation (« non p ») et de connexion : ¬(p ∧ ¬q).

Les Stoïciens disaient, plutôt que d’établir des tables de vérité comme nous aujourd’hui : « Du vrai suit le vrai... Du faux suit le faux... Du faux suit le vrai... Mais du vrai, le faux ne peut s’ensuivre. » (Diogène Laërce, Vies, doctrines et sentences des philosophes illustres, livre VII, 83).

Ni miracle, ni mystère... voici la rationalisation logique menée ou revenue à terme. Effort de la raison, ou plutôt de l’intelligence comme puissance de jugement réfléchi, d’où découlent tous les types de raisonnement rigoureux, tant qu’on reste dans l’univers des opérations potentielles. D’où découle, pour ne prendre qu’un exemple mais un exemple remarquable, le raisonnement par récurrence. Raisonnement constitué d’un enchaînement d’implications, que d’aucuns, comme le génie des mathématiques Henri Poincaré, ont célébré comme l’exemple même du raisonnement logique, a priori et néanmoins synthétique, fécond en connaissances, pur et constructif si l’on veut, démarche logique et progressive qui caractérise les mathématiques.

Logique de l’enquête et quête éternelle de certitudes

Levons le voile.

Les citations qui ont été lues et commentées tout au long de cette conférence sont tirées d’une même œuvre, magistrale, La Quête de certitude de John Dewey (1929). Et du même chapitre, « Le jeu des idées ». Pourquoi ne pas l’avoir dit ? Par coquetterie ? Non pas. Sans avoir trop de chances de me tromper, je crois pouvoir dire que peu d’entre vous ont déjà entendu parler de John Dewey. À quoi bon alors donner son nom avant que d’avoir fait sa connaissance, avant que de l’avoir rencontré ?

Dewey est un grand auteur. Certes, il n’est pas parmi la liste des grands auteurs du programme de terminale de philosophie. Il n’est pas inscrit au Panthéon. Il est même boudé des Français. Quand j’étais lycéen puis étudiant, je n’ai entendu parler de lui par aucun de mes professeurs. Et pourtant ce fut un auteur à succès dans la première partie du XXe siècle, sans doute le philosophe américain le plus renommé à l’époque. Il est aujourd’hui redécouvert, traduit (enfin) et de plus étudié en France. Qu’est-ce que cela prouve ? Que tous les grands auteurs ne peuvent être retenus dans un programme de philosophie ? Peut-être. Qu’il y a des modes en philosophie ? Très certainement. Les philosophes qui aiment tant critiquer les préjugés des autres sont les plus belles victimes des préjugés ! La sagesse suppose d’intérioriser l’idée que nul ne doit se targuer d’avoir moins de préjugés que son voisin.

Une autre des grandes œuvres de Dewey sur la science contient de remarquables passages sur les mathématiques, Logique. La théorie de l’enquête (1938). Pourquoi ne pas l’ouvrir, un jour prochain ?

En guise de conclusion

Avec ses limites et sa bonne volonté, parfois, la démarche philosophique est d’abord étonnement et, dans la foulée, questionnement. Les mathématiques n’ont cessé d’étonner le philosophe. Plus encore que les discours des politiques, les paroles des prêtres ou bien les opinions vulgaires, ses réflexions l’ont incité à poser des questions. À poser quatre grands types de questions, d’après des spécialistes de la philosophie des mathématiques, Marco Panza et Andréa Sereni (Plato’s problem, 2013, préface) :

• un questionnement sur les fondements des mathématiques ;
• une interrogation sur l’essence du savoir mathématique ;
• une réflexion portant sur les méthodes de preuve (Panza s’étant par exemple intéressé au mode de raisonnement qui utilise des diagrammes permettant de visualiser des résultats... comme Alain Busser, à l’île de La Réunion, dans son enquête sur la pensée présidant à la naissance de l’informatique) ;
• une mise en cause de l’applicabilité des mathématiques, ce qu’on appelle également son effectivité, particulièrement dans les sciences de la nature, sciences physiques où les théories mathématiques apparaissent comme un langage ou une structure nécessaire, mais aussi, plus récemment, dans les sciences biologiques, biochimiques...

Les deux premiers questionnements mettent clairement en jeu le caractère idéal des mathématiques, parfaitement assises sur des principes logiques indubitables ou bien capables de délivrer une vérité qu’on qualifiera d’apodictique pour en préciser la nature absolument universelle et nécessaire... vérité portant sur des opérations purement symboliques, non effectives.

Les deux suivants impliquent également l’idéalité mathématique, parce qu’ils prolongent la réflexion portant sur le caractère formel des énoncés compossibles, non incompatibles. Le dernier de ces questionnements participe d’une réflexion sur les mathématiques comprises comme instituant une langue artificielle, ad hoc, « parfaite » comme on a pu dire. Si les mathématiques sont de part en part une science formelle elles divergent du reste des sciences devant être comprises comme des sciences naturelles, qui toutes délivrent une connaissance portant sur la nature des choses, le monde qui nous entoure et nous comprend. D’une part les mathématiques se réduiraient à des idées, un enchaînement d’idées, eidos, formes intelligibles. Elles ne diraient rien de l’être matériel ; elles ne pourraient rien dire du monde réel, des choses qui existent ; elles sont un discours à part, tirant sa cohérence de la non-contradiction et non de l’adéquation des propositions à l’état de choses qui est, la réalité ! Et pourtant elles servent de langage pour les autres sciences. Elles sont pour la physique ce qui structure la théorie, lui donne des ailes, lui permet de faire des prévisions pouvant se révéler justes !

Nous avons parlé des idées comme d’objets mathématiques, en donnant quelques exemples, les angles, les nombres, l’espace ou les espaces, les . Dès lors quelque chose comme une objectivité de ces objets a été reconnue. Mais il faut y prendre garde. Quelle est cette objectivité ? Cette objectivité n’est pas comparable à l’objectivité de cette table ou de ces images projetées sur l’écran.

Il y a plusieurs manières d’appréhender cette différence d’objectivité. Fréquemment on a remarqué que les uns, objets ordinaires — la table ou les images — sont hic et nunc, ici et maintenant, incarnés dans une matière, tangibles, visibles et repérables dans le monde quand les autres — les objets mathématiques — seraient ailleurs, on ne sait où, en même temps dans la pensée de tous ceux qui les pensent, les ont pensées et pourront les penser, autant dire situés dans l’éternité par opposition à la durée ! Les uns sont quand les autres seraient... si l’on insiste sur les temps employés pour exprimer cette pensée, un indicatif ou un conditionnel, alors il faut parler d’une objectivité ostensible et d’une objectivité hypothétique.

Peut-être un peu moins souvent, on a aussi souligné que cette objectivité est singulière, en tant qu’objectivité d’idéalités, et différente de l’objectivité des objets ordinaires à laquelle nous sommes habitués en ce qu’elle est rétrospective ! Et on pas projective (on me parle d’un chat et je m’attends à quelque chose qui est objectivement un chat... et pas un tigre...). Ce n’est pas à l’origine, au début des temps, à l’époque même qui voit la naissance des divers objets mathématiques, que cette objectivité est assurée. Mais c’est bien après, parfois même des siècles après, voire des millénaires, quand la pensée s’est suffisamment développée. Après coup ces objets deviennent enfin ce qu’ils pouvaient être ! Ou ce qu’ils devaient être, ce qu’ils ne pouvaient manquer d’être !

Paradoxe fondamental de l’histoire des sciences, le progrès est progression à la fois vers des connaissances plus complexes (par le développement du savoir dans l’inconnu) et plus simples (par reprise du savoir à l’origine) : c’est récemment et non depuis des siècles que les mathématiques ont reçu des bases sûres. Les mathématiciens ont d’abord fondé provisoirement leurs recherches sur des bases primitives (ou premières) – même s’ils croyaient alors ou pouvaient croire qu’elles étaient définitives – ces bases ont depuis été renversées, parfois assez brutalement, et c’est très récemment que les mathématiciens sont parvenus à fonder leurs recherches sur des fondements raisonnables. Et il n’est pas faux de dire qu’ ils continuent depuis à œuvrer collectivement à leur fondation !

L’objectivité est ainsi non un point de départ mais un point d’arrivée. C’est une conquête de l’esprit humain. On sait mieux de quoi on parle aujourd’hui qu’hier... en attendant demain...

Ouvertures

Les mathématiques ont pour cela une histoire, qui est passionnante. Histoire à laquelle nous pouvons tous nous intéresser, et qui nous réserve des surprises.

Pour poursuivre par vous-mêmes dans cette voie je vous conseille de lire une bande dessinée, Logicomix, qui met en scène le mouvement de l’axiomatisation des mathématiques, de l’arithmétique, avec une de ses figures majeures en personnage principal, Bertrand Russell, auteur avec Whitehead, au tournant du XX^e siècle des Principia mathematica.

Dans les bibliothèques on trouve des bouquins assez accessibles. Et pas totalement à côté de la plaque comme bon nombre de manuels de Terminale :

• Introduction à la philosophie des mathématiques de Bertrand Russell,
• La Science et l’hypothèse d’Henri Poincaré.

L’histoire des mathématiques doit être replacée dans l’histoire des idées de manière plus générale. Evoquant le sens du jeu de la vie de Conway, le livre de Daniel Dennett, Une théorie évolutionniste de la liberté (2003) est très utile.

Sur le Net, on trouve aussi quelques sites particulièrement intéressants. Le meilleur d’entre eux est celui auquel participe, entre autres Étienne Ghys : Images des maths, du CNRS.

On y trouve de tout, une information sur l’ardoise de Ramanujan. Un compte-rendu de manifestation, une réflexion sur l’enseignement des mathématiques... et surtout des articles de vulgarisation remarquables classés comme les pistes de ski. Personnellement je suis forcé de me contenter des « pistes vertes », par exemple un article sur les horloges à eau de Lorenz (auteur de la théorie de l’effet papillon). Mais cela va jusqu’à la piste noire, par exemple un article sur les travaux d’Artur Avila (sur les systèmes dynamiques), jeune franco-brésilien ayant reçu une médaille Fields en 2014.

Le site de l’IREM de la Réunion n’a bien sûr pas la prétention de l’égaler, mais il vaut aussi le détour.