(photo prise par Marek_Szczepanek sous license CC)

L’algorithme de Héron est utilisé dans les calculatrices, et vraisemblablement aussi dans les ordinateurs, pour calculer les racines carrées. On est donc dans du concret ! Ceci dit, c’est bien joli de sortir de son chapeau une suite qui converge vers $\sqrt{5}$, et qui est définie par $w_{n+1}=\frac{w_n+\frac{5}{w_n}}{2}$, pour calculer une valeur approchée de $\sqrt{5}$ en calculant par exemple $w_{20}$... C’est tout de même mieux de donner un indice, à défaut d’une démonstration, du fait que la suite est convergente, et que sa limite est bien $\sqrt{5}$.

Pour le deuxième point, on peut (sans parler de continuité) faire résoudre l’équation $x=\frac{x+\frac{5}{x}}{2}$. Pour la convergence c’est moins facile (à moins d’utiliser le théorème des accroissements finis...). Pour expliquer de quel chapeau le lapin est sorti, avec deux suites $u_n$ et $v_n$ telles que $u_{n+1}=\frac{u_n+v_n}{2}$ et $v_{n+1}=\frac{5}{u_{n+1}}$ (qui, hélas, ne sont pas adjacentes parce que pas monotones), on peut partir de l’idée que

• $x\simeq \sqrt{5} \Rightarrow \frac{5}{x}\simeq \sqrt{5}$
• Si l’une des deux valeurs approchées est par défaut, l’autre l’est par excès et vice-versa.
• À partir de deux valeurs approchées de $\sqrt{5}$ telles que $x\leqslant \sqrt{5} \leqslant y$, on en construit facilement une meilleure en prenant leur moyenne arithmétique (idée conçue spontanément par plusieurs élèves qui trouvent ça naturel).

On peut envisager de pousser un peu plus loin cette idée en utilisant le caractère multi-agents du logiciel Scratch, et en confiant le calcul de $u_n$ à un lutin (ci-dessous appelé moyenneur puisqu’il calcule une moyenne arithmétique) et le calcul de $v_n$ à un autre lutin (ci-dessous appelé inverseur puisque pour diviser 5 par $u_{n+1}$, on le multiplie par son inverse). Les deux lutins doivent être synchronisés par un "maître", lequel sera incarné par la "scène" de Scratch :

Comme on le voit, son rôle se borne à incarner la boucle. Pour le traitement effectué dans la boucle, il est partagé entre les deux lutins. Le moyenneur calcule des moyennes, quand on (la scène) le lui demande :

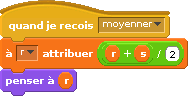
Et l’inverseur calcule juste des quotients :

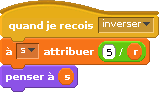
Certes, en simulant du calcul parallèle, on s’éloigne un tantinet de l’algorithmique, mais cette description permet de montrer le fonctionnement de l’algorithme sans avoir à parler de suite. Voici ce que donne l’exécution du script (le moyenneur à gauche, avec deux pinces parce qu’il opère sur deux nombres, et donc l’inverseur à droite, à l’envers comme tout inverseur qui se respecte) :

De même, le traitement simultané des deux suites peut être fait par un logiciel de géométrie dynamique, en représentant simultanément les deux suites par un point (de coordonnées $(u_n ;v_n)$) et en appliquant une dizaine de fois une macro (la convergence est suffisamment rapide pour cela). Voici la version CaRMetal :

En manipulant la figure ci-dessus, on constate que l’algorithme converge vers l’une ou l’autre des deux limites possibles, selon la valeur initiale. On peut parler de bassin d’attraction.

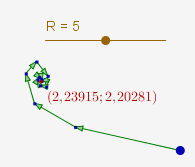
Ceci dit, la suite $w_n$ ci-dessus se prête à une figure dynamique, en remplaçant 5 par un curseur R :

Le CaRScript ayant permis cette construction est sans doute "non exigible" :

u=Point("U0",0,1);
SetFixed(u,true);
for(var n=1;n<21;n++){
    u=Point("U"+n,n,"(y(U"+(n-1)+")+R/y(U"+(n-1)+"))/2");
}

Remarque :

La version "toile d’araignée" n’est pas très pertinente dans le cas présent, la suite converge trop vite pour qu’on ait le temps d’y voir quelque chose...

from threading import *
import time

r, s = 1.0, 0.0

class Moyenneur(Thread):
    def __init__(self):
        Thread.__init__(self)
        print "Maintenant on a un moyenneur"
    def run(self):
      global r
      for n in range(8):
          r += s
          r /= 2
          print "Moyenne : ", r
          time.sleep(2)

class Inverseur(Thread):
    def __init__(self):
        Thread.__init__(self)
        print "Maintenant on a un inverseur"
    def run(self):
        global s
        for n in range(8):
          time.sleep(1)
          s = 5.0/r
          print "Division : ", s
          time.sleep(1)

from threading import *
import time

r, s = 1.0, 0.0

class Moyenneur(Thread):
    def __init__(self):
        Thread.__init__(self)
        print "Maintenant on a un moyenneur"
    def run(self):
      global r
      for n in range(8):
          r += s
          r /= 2
          print "Moyenne : ", r
          time.sleep(2)
    		

class Inverseur(Thread):
    def __init__(self):
        Thread.__init__(self)
        print "Maintenant on a un inverseur"
    def run(self):
        global s
        for n in range(8):
          time.sleep(1)
          s = 5.0/r
          print "Division : ", s
          time.sleep(1)
    		

moyenneur = Moyenneur()
inverseur = Inverseur()
moyenneur.start()
inverseur.start()