Mathésport
Rappel de l’épisode précédent : Le finale de la fête de la science s’est fait sur le bitume de l’Université du Tampon, sur un graphe dessiné à la craie, les pions à déplacer sur le graphe étant les joueurs eux-mêmes (donc on jouait en équipe).
Le succès de l’activité a été tel que la semaine des maths a été l’occasion de répéter cette expérience, non une fois, mais presque tous les jours. Avec des variantes.
Bambous
Le graphe du jeu des deux parkings a été dessiné à la craie, dans la cour du collège de la ligne-des-bambous :
On voit ici l’équipe orange, en train de jouer à ce jeu :
Le nombre de joueurs occupés par cette activité est, à chaque instant, un multiple de 3 : 6 joueurs sont sur le terrain, et à chaque fin de partie, les 3 joueurs gagnant affrontent une nouvelle équipe de 3 joueurs.
Cela a mené au dessin d’un second graphe, similaire au précédent, à côté de celui-ci, pour accueilir encore plus de monde :
Ce qui offrit alors l’inoubliable spectacle de deux jeux des deux parkings en même temps :
On constate une évolution stylistique du graphe depuis la fête de la science :
- Les sommets tendent à être dessinés plus grands (et plus circulaires)
- les arêtes deviennent plus courtes.
Gaston-Crochet
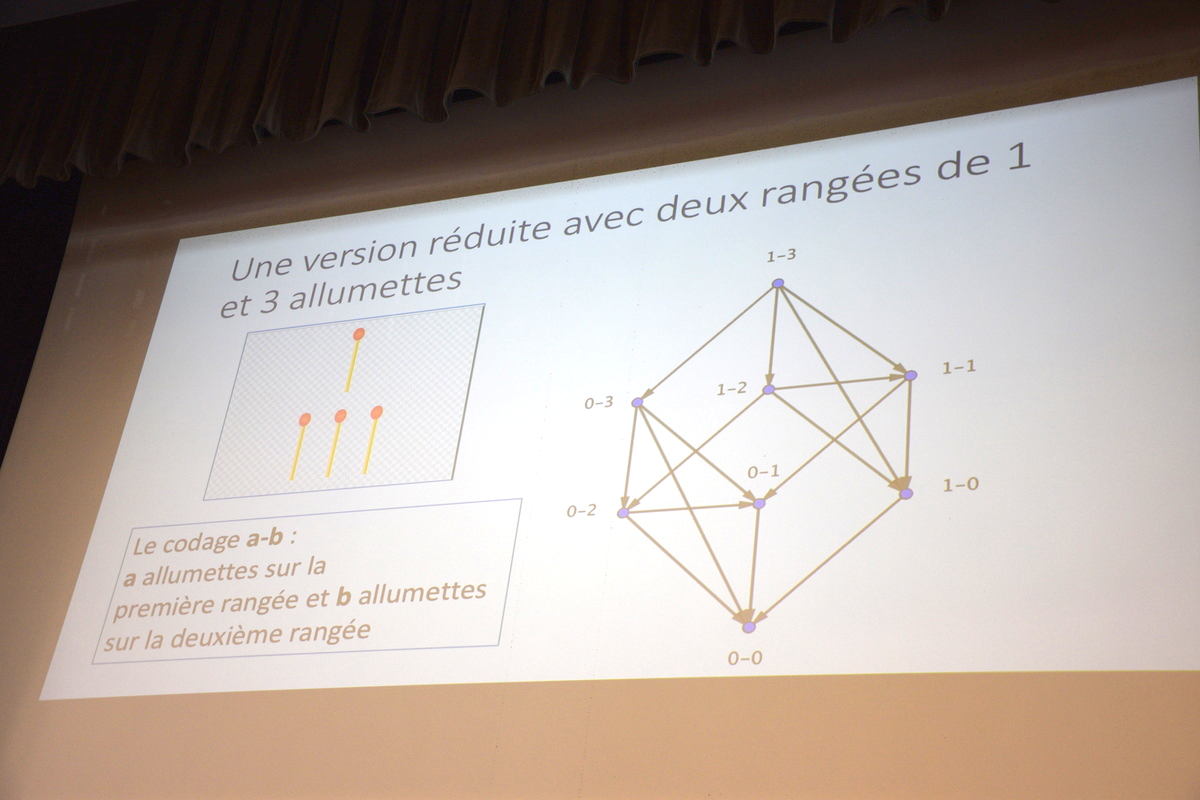
L’expérience du collège de la ligne-des-bambous a suggéré une variante pour le collège Gaston-Crochet (Plaine-des-Palmistes) : Essayer avec le jeu de la madelinette. Ce graphe [1] est plus simple que celui des deux parkings :
- 7 sommets au lieu de 13
- 11 arêtes au lieu de 22
Néanmoins, il occupe autant de joueurs : 2 équipes de 3 joueurs.
Voici le graphe de la madelinette, resplendissant de toute sa splendeur sous le soleil palmiplainois :
Une différence importante avec le jeu des deux parkings est que dans ce dernier les joueurs sont placés à leur position de départ avant de commencer le jeu, alors que pour la madelinette, les équipes doivent se placer dans le graphe pendant la première phase de jeu. Ils le font par placement l’un après l’autre :
Cette phase tend d’ailleurs à durer longtemps et les élèves finissent par se déconcentrer.
Pour savoir quelle équipe va commencer le jeu, on peut utiliser un procédé classique comme chifoumi :
Comme la phase de placement des joueurs tend à désintéresser ceux-ci du jeu, et que des collégiennes ayant déjà joué au jeu des deux parkings lors de la fête de la science, ont exprimé le regret de ne pas voir « le même graphe que la dernière fois », un second graphe a été dessiné à côté de celui de la madelinette, cette fois-ci pour rejouer au jeu des deux parkings :
On remarque une nouvelle évolution stylistique : Les sommets dessinés sous forme carré (et non plus circulaire), les arêtes plus courtes, et les sommets coloriés pour les rendre plus visibles. Cette façon de dessiner se prête plus facilement à une réalisation à la peinture (ou par collage de scotch sur l’asphalte).
Le jeu fonctionne très vite :
Bilan en collège :
- le graphe est plus facile à dessiner et plus visible par les joueurs si on dessine les sommets carrés
- le jeu des deux parkings « marche » mieux que celui de la madelinette
- le jeu est plus facile à jouer si une des équipes porte des dossards de couleur immédiatement identifiable.
- Le jeu est d’un abord presque immédiat dès le collège.
On a donc naturellement tenu compte de ce bilan, pour recommencer l’expérience cette fois-ci en école élémentaire :
400
À l’école Louis-Clerc Fontaine (également appelée « de la ligne des 400 » en raison de l’altitude à laquelle elle est située) au Tampon, des dizaines d’élèves de CM1 et CM2 ont à leur tour joué au jeu des deux parkings. L’ardeur du soleil tamponnais a incité à dessiner le graphe à l’ombre :
Voici une situation typique de début de jeu, avec 9 élèves :
Les trois filles au premier plan, qui font face à l’animateur, sont une future équipe, qui affrontera l’équipe gagnante après la première partie. Les trois filles alignées à droite de la photo forment une équipe en début de jeu, positionnée sur le « parking » de départ. Et leur font face 3 autres enfants qui forment l’autre équipe, là aussi en position alignée.
Comme un seul membre de l’équipe effectue un mouvement à chaque tour, il y a des décisions collégiales à prendre, ce qui incite les élèves (ici l’équipe des rouges) à « mettre un haut-parleur sur leur pensée » :
Ici une joueuse est bloquée, par une de ses coéquipières et une joueuse de l’équipe des rouges occupant le sommet central :
Mais sa coéquipière au fond n’est pas bloqué, elle peut aller vers le sommet qui est à droite sur la photo. Son équipe n’a donc pas encore perdu.
Un joueur de l’équipe des rouges (au fond) prend l’initiative de désobéir à son capitaine :
C’est finalement un autre joueur qui va bouger :
Erreur de sa part, l’équipe des rouges va finalement gagner le jeu :
Pions
Le jeu des deux parkings était également présent à l’intérieur, sous sa forme miniature avec les pions.
Voici deux fins de partie au collège des la ligne-des-bambous :
Les bleus viennent de remporter la course :
Là aussi les bleus gagnent mais en bloquant les rouges :
On en déduit, d’après le théorème de Hoarau, que ce sont les bleus qui ont commencé la partie.
De façon générale, les élèves ayant joué dehors avant de retrouver le graphe en petit, reconnaissent immédiatement le jeu. Dans l’autre sens c’est moins systématique : Les élèves ayant joué avec les pions sur le petit graphe n’identifient pas immédiatement le jeu des deux parkings quand ils le voient en grand.
Le graphe des deux parkings peut être fait à la peinture pour permettre aux élèves d’y jouer plus souvent, voire d’organiser des championnats périodiquement. Une règle a été proposée en ajout des règles initiales : Si, pendant un laps de temps trop élevé (compte à rebours prononcé à voix haute), une équipe refuse de jouer, le jeu est déclaré terminé et l’équipe minimisant la distance totale à l’arrivée a gagné.
Escape games
Le passage de la caravane de l’IREM au collège de la ligne des bambous a été l’occasion de voir ce que faisaient, dans le cadre de la semaine des maths, les enseignants « hors IREM » de ce collège. Et le thème des escape games a été très présent ce jour là. Puis le congrès M.e.J. a été l’occasion pour les ateliers IREM consacrés aux escape games de mettre en œuvre leurs réalisations.
Bambous
Certains élèves ont été « confinés » en plein air, avec la tâche de résoudre des énigmes leur permettant de découvrir un trésor :
Il a été nécessaire pour résoudre certaines de ces énigmes, d’utiliser la calculatrice :
On n’est pas là face à un escape game classique : Les énoncés des énigmes sont un peu longs et il n’y a pas de porte à ouvrir pour s’évader. Par contre, l’ambiance y était avec un compte à rebours et une musique stressante !
Algo débranchée
Toujours au collège de la ligne des bambous, une activité annoncée comme « algorithmique débranchée » s’est révélée très proche d’une énigme de type « escape game » : Il s’agissait de trouver, l’une après l’autre, les lettres d’un mot, en effectuant des parcours sur le sol :
Le parcours était décrit dans un langage algorithmique :
Proposée par un ancien animateur de l’IREM, cette activité a séduit le groupe animations, qui l’a réinvestie à l’école Louis-Clerc Fontaine :
On constate une modification de l’activité : Les directions cardinales ont été rajoutées aux cercles numérotés. En effet la manière dont sont tracées les flèches sur l’algorithme rend leur interprétation un peu ambigüe.
Bombe
Un terroriste a caché une bonbe [2] quelque part dans la salle. Vous avez 45 minutes pour la désamorcer :
Une des énigmes consistait à dessiner un QR-code menant à un indice supplémentaire :
Une autre était un habillage « postal » des célèbres tours d’Hanoï :
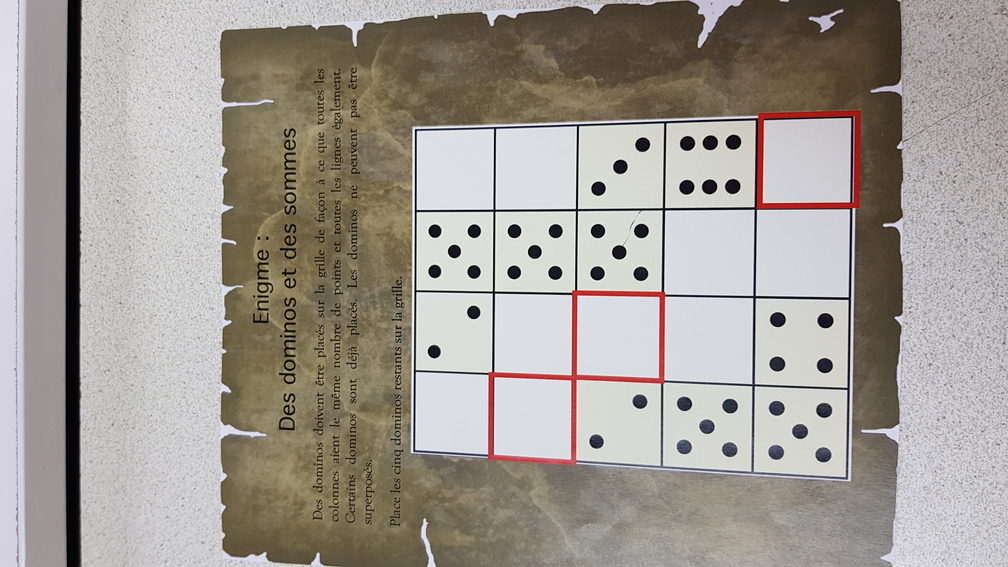
Une autre consistait à remplir un tableau de nombres, à partir de leurs sommes :
On constate le soin apporté au look des énigmes :
La programmation n’était pas en reste avec la carte microbit :
Un moment fort est celui où on ouvre le fameux coffre :
Les gagnants posent fièrement :
Galilée
Un autre escape game avait pour thème un personnage historique à découvrir.
On a même scratché :
Les gagnants posent fièrement :

Abaque
Pas d’abaque de Gerbert cette fois-ci, mais l’abaque à jetons a été présenté à chaque fois que possible. On a donc semé beaucoup de haricots cette année (avec une surprise dans le dernier onglet).
MeJ
Au Moufia, lors du congrès MATh.en.JEANS, l’abaque à jetons a été à nouveau présenté :
L’animation de cet atelier permet de bien situer les difficultés en calcul. Et la manipulation de l’abaque à jetons s’inscrit pleinement dans les 21 mesures, en particulier celles sur la méthode dite de Singapour.
Registres
Une autre forme de calcul avec des graines de haricot est donnée par le modèle des registres de Minsky.
Voici le diaporama du séminaire IREM du 6 mars 2019, consacré à ce modèle de calculabilité :
Et les fiches amenées à la semaine des maths pour lancer l’activité :
Ces fiches se sont révélées peu utiles finalement.
Un élève du collège Gaston-Crochet pose le calcul 2+2, en plaçant 2 graines dans le registre r1 et 2 autres graines dans le registre r2 :
Reste à trouver comment effectuer l’addition, en n’utilisant que les opérations suivantes :
- regarder si un registre est vide
- répéter des actions jusqu’à ce qu’un registre soit vide
- enlever une graine d’un registre, si possible
- ajouter une graine dans un registre.
Lorsqu’une graine est enlevée d’un registre, elle est placée dans la boîte, ou directement sur la table :
Pour calculer 2+2, on répète, jusqu’à vacuité de r1, la séquence suivante :
- enlever une graine de r1
- ajouter une graine à r2

Il devient vite évident que cela peut se résumer à une seule action, à mener jusqu’à ce que r1 soit vide :
- Transférer une graine de r1 à r2 :
Comment peut-on prouver que cet algorithme effectue bel et bien une addition ? Pour cela il faut un invariant de boucle, en l’occurrence il s’agit de montrer que, d’une part, le transfert d’une graine, d’un registre à l’autre, ne modifie pas le nombre total de haricots, d’autre part, qu’à la fin tous les haricots sont dans r2. Pour cette dernière étape, c’est une conséquence directe du fait que l’algorithme s’arrête précisément lorsque r1 est vide ; pour l’invariant, on utilise le calcul littéral en 3e :
Et pour la soustraction, en 4e, on a abordé l’algèbre avec un exemple :
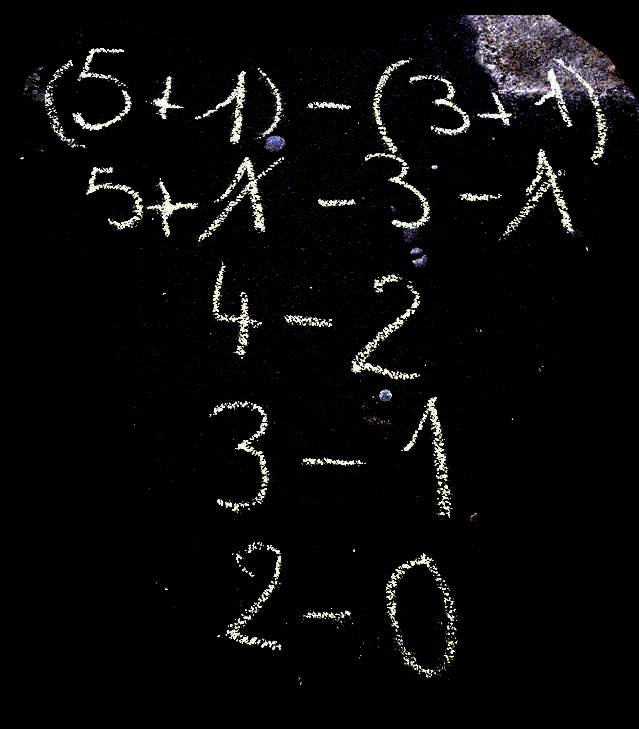
Dans ce cas, il s’agissait de montrer qu’on ne modifie pas la différence en ajoutant une graine aux deux registres, ou en enlevant une graine aux deux registres. Et comme a-0=a, on ne garde que la différence à la fin dans le registre r1.
Sowing
Mais il n’y a pas que sur un abaque qu’on peut poser des graines, il y a aussi le plateau de jeu de Sowing. Les vendredi et samedi soirs ont été l’occasion, au Moufia puis à Bellepierre, de jouer à Sowing.
La joueuse de gauche s’apprête à effectuer un semis. Pour cela elle prend toutes les graines qui sont dans une case, les garde un instant dans sa main, puis les sème, une par une, vers sa droite.
Mais elle ne peut pas semer les 4 graines de la case du milieu, car si elle le faisait,
- elle prendrait les 4 graines dans sa main, vidant la case du milieu ;
- elle poserait une graine dans la case en comportant actuellement 2, faisant passer le nombre de graines dans cette case, à 3 ;
- elle poserait la seconde graine dans la case en comportant actuellement 3, faisant passer le nombre de graines de cette case, à 4 ;
- elle poserait la troisième graine dans l’avant-dernière case (actuellement vide) ce qui ferait qu’il y aurait une graine dans cette case ;
- mais elle poserait la dernière graine dans la dernière case, actuellement vide, et cela est interdit par la règle du jeu :
La dernière graine d’un semis ne doit pas tomber dans une case vide
Pour des raisons similaires, Gauche ne peut pas non plus semer depuis une des trois cases qui sont à sa droite.
Alors Gauche décide de semer l’unique graine tout à gauche :
Elle aurait aussi pu semer les deux graines presque tout à gauche, faisant passer la configuration à 10533.
La partie ci-dessous est terminée puisqu’aucun des deux joueurs ne peut semer vers sa droite, sans que la dernière graine tombât dans une case vide :
Dans ce cas, le joueur ayant effectué le dernier semis valide gagne le jeu.
Voici une situation où Gauche (en bas sur la photo) ne peut plus jouer, alors que Droite (en haut sur la photo) peut encore semer depuis une des deux cases de 3 graines, puisque dans chaque cas la dernière graine tombe dans une case occupée :
Comment se fait-il que Gauche ne puisse semer les trois graines alors que Droite le peut ? C’est parce que chaque joueur sème vers sa droite, or la droite de Droite est la gauche de Gauche (et la droite de Gauche est la gauche de Droite). Ce jeu est dit partisan parce que les mouvements des deux joueurs ne sont pas les mêmes [3]. Dans un tel jeu, il se peut qu’une position soit plus favorable à l’un des joueurs qu’à l’autre, quel que soit celui qui doit jouer. Pour quantifier cet avantage, Conway donne une valeur à chaque jeu, ce qui lui permet de construire successivement
- les nombres entiers [4] ;
- les fractions dyadiques (appelées flottants en Python) ;
- les autres fractions et nombres irrationnels (bref, les réels) par passage à la limite ;
- les nombres infinis et infinitésimaux, amenant à la notion de nombre hyperréel.
Mais au passage on découvre beaucoup de jeux qui ne sont pas des nombres, par exemple celui-ci où chaque joueur ne peut semer que la graine qui est toute seule dans sa case, aboutissant à des cases contenant trop de graines pour être semables par qui que ce soit :
Conway appelle ce jeu étoile et c’est le plus simple des jeux de Nim. Voici un calcul montrant que le jeu de Sowing où 6 cases contiennent 2 graines chacune, est aussi égal à l’étoile :
Le calcul a été fait dans cette salle :
Il y a aussi été fait ce calcul, montrant que le jeu où une case de 2 graines est suivie par 3 cases d’une seule graine, est à l’avantage de Gauche :
Cependant cet avantage est inférieur à 1 et Conway l’évalue à 0,5 : C’est le premier exemple de jeu dyadique apparu dans Sowing.
Le dernier jour du congrès, l’amphi a été envahi par de nouveaux plateaux de jeux de Sowing :
Cela a permis à ceux qui n’avaient pas pu bénéficier de cet atelier dans les jours précédents, de découvrir par la manipulation ce jeu bien plus facile à jouer qu’à expliquer :
Et pour ce qui est de manipuler, on a manipulé ! On a verbalisé aussi :
Cet entracte fut suivi de la conférence de clôture, consacrée ... à Sowing !
Voici le diaporama de la conférence :
Snort
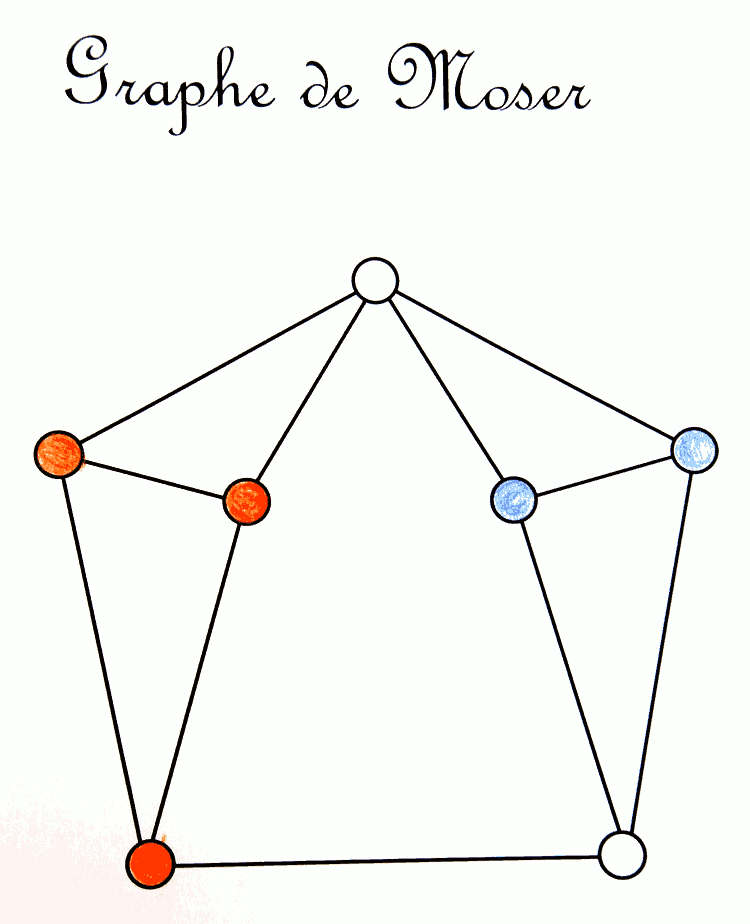
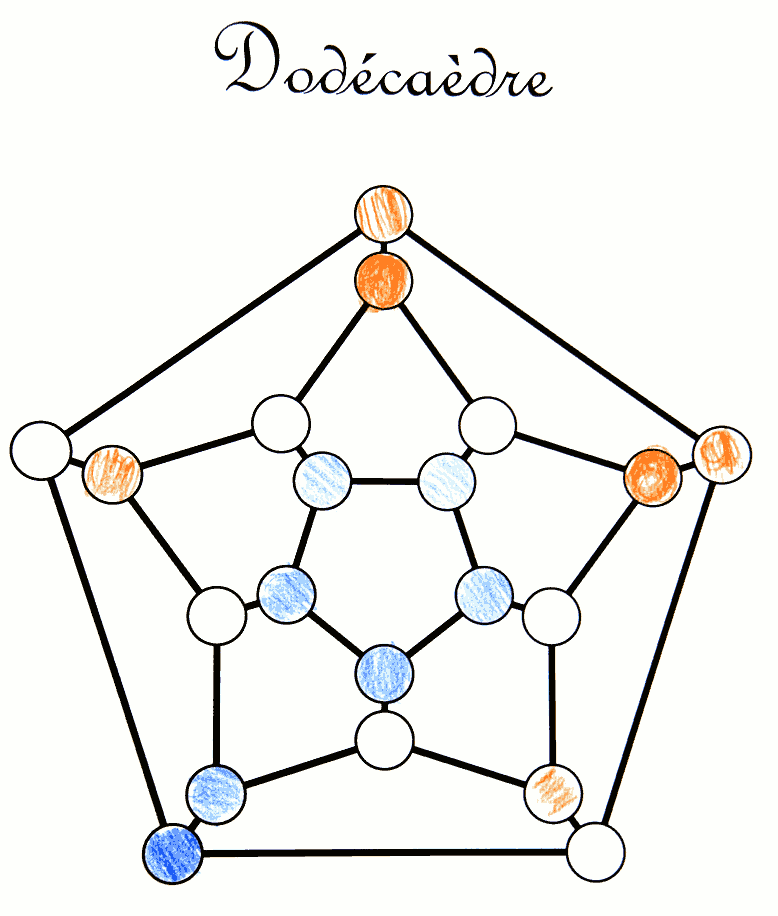
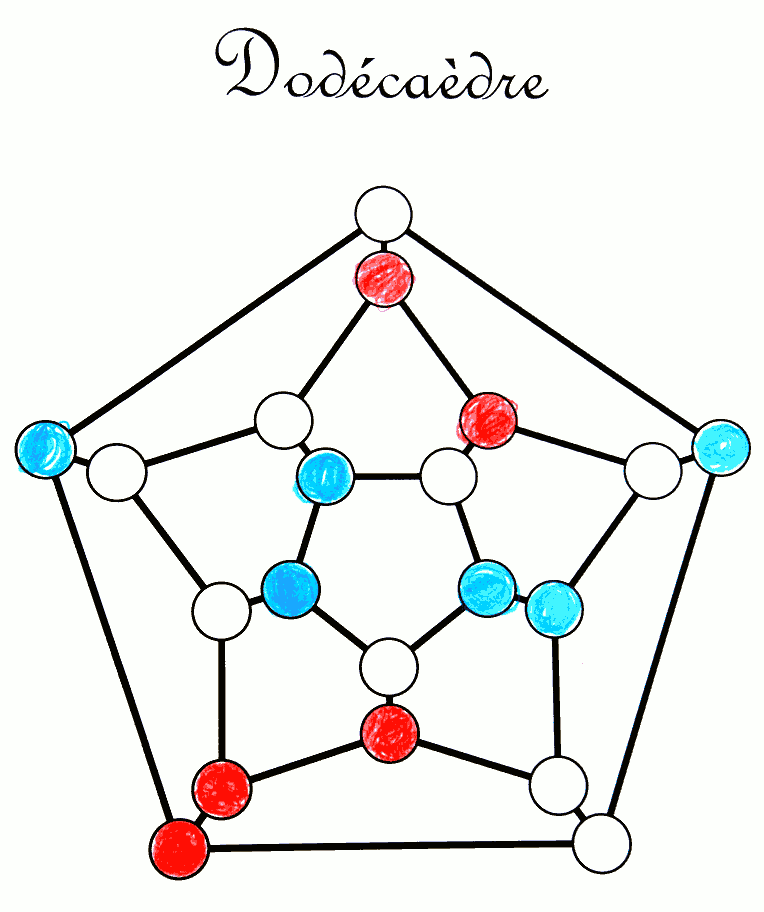
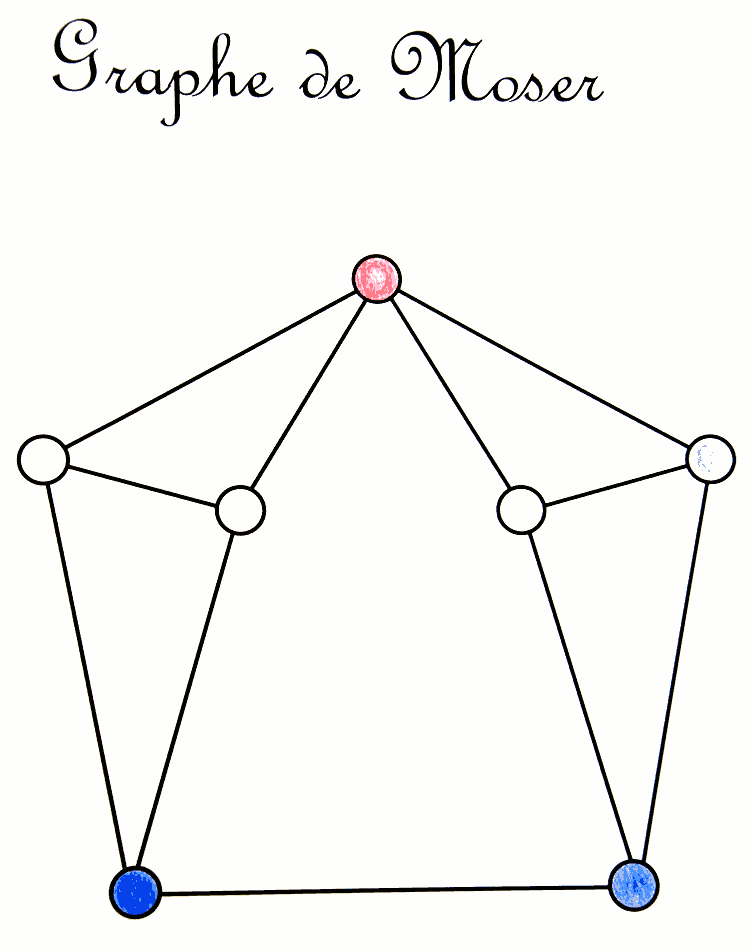
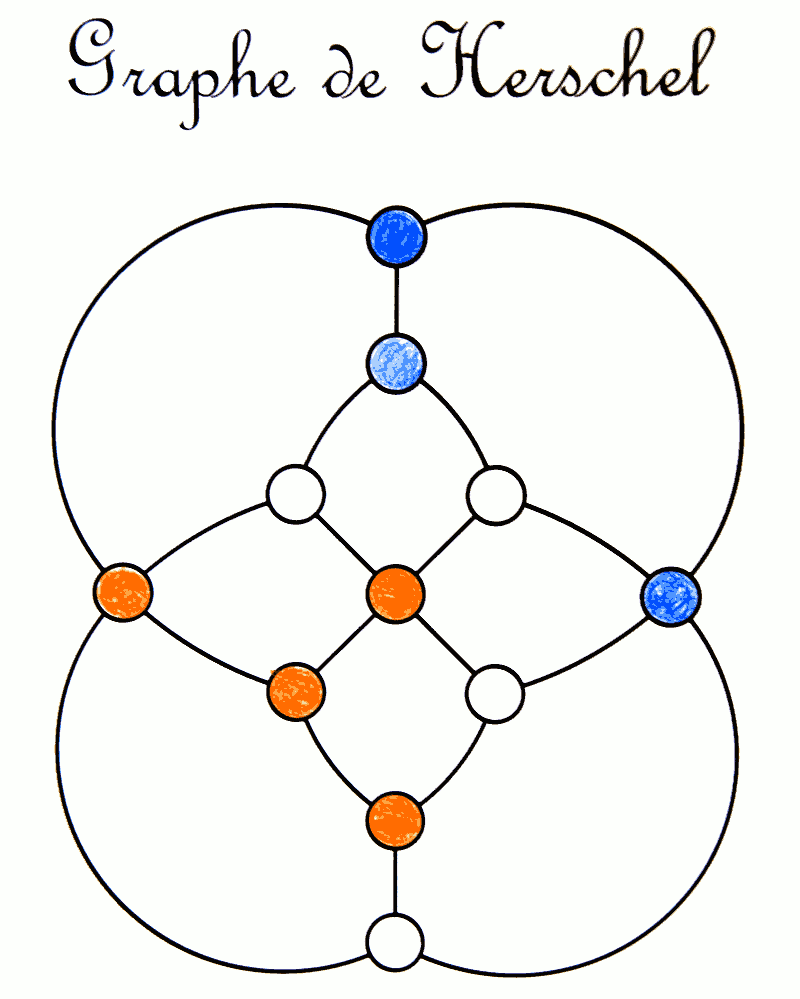
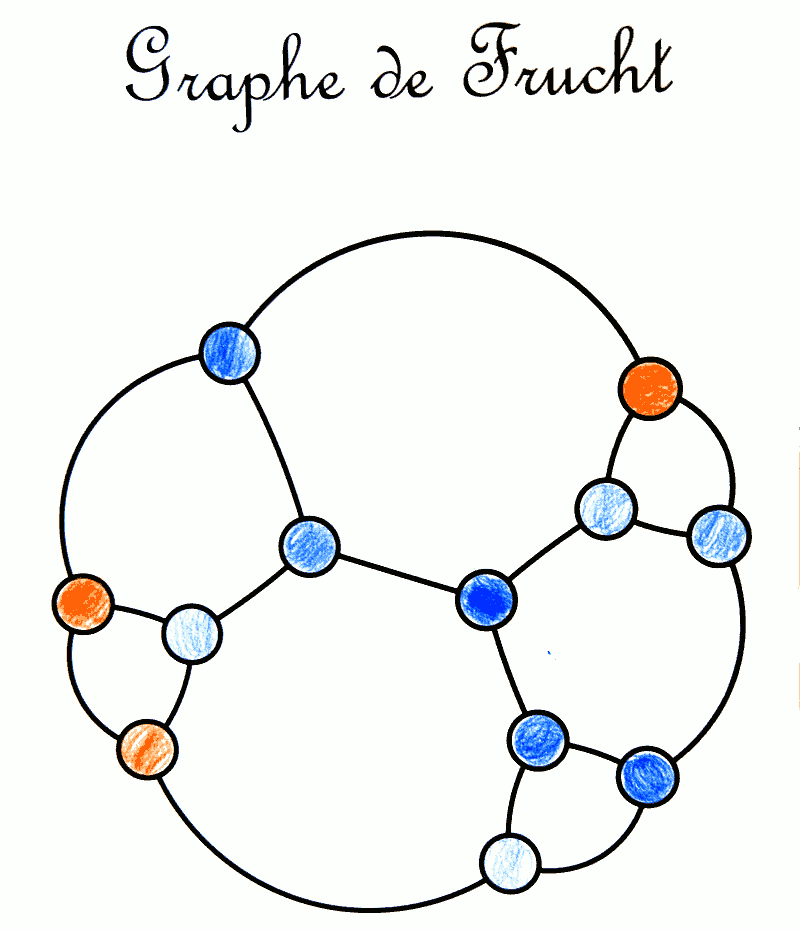
Le jeu de Snort consiste à colorier les sommets d’un graphe, chacun son tour, de manière à ne jamais avoir de sommets adjacents de couleurs différentes. Le nom de ce jeu vient de son inventeur Simon Norton mais on retrouve la simplicité des jeux de John Conway : La règle du jeu s’apprend en quelques secondes et on est vite accro. Ce sont des élèves de 6e peu enthousiastes à l’idée de faire des mathématiques qui ont fait les coloriages ci-joints, avec un engagement surprenant de leur part.
Parties
Bleu s’apprête à colorier un sommet, elle en a le droit parce qu’aucun voisin de ce sommet n’est rouge

Puis Rouge constate que tous les sommets libres sont adjacents à des sommets bleus, ce qui signifie qu’elle a perdu (signification trouvée spontanément par tous les joueurs débutants).
Ici Bleu est en train de gagner, en coloriant un sommet dans sa couleur, alors que tous les sommets restants sont adjacents à au moins un sommet bleu, ce qui fait perdre Rouge :
Erreurs
Ici Bleu essaye de colorier un sommet adjacent à un sommet rouge (à droite du graphe) puis se ravise et arrête son coloriage, admettant avoir perdu le jeu :
C’était d’ailleurs au tour de Rouge de jouer !
Ici Rouge a colorié un sommet adjacent à un sommet bleu, probablement par manque de vision des arêtes circulaires :
La même erreur s’est produite ici, mais deux fois :
Et là aussi :
Avec d’ailleurs un décalage : C’était à Rouge de jouer !
Ici, Bleu, dans la foulée, a décidé de colorier tous les sommets restants :
Doug
Une analyse du jeu de Doug a été faite par coloriage, par les mêmes élèves de 6e mais aussi des élèves de 4e : Le graphe orienté étant considéré comme plateau d’un jeu de Nim, on colorie en vert les cases gagnantes et en rouge les cases perdantes. Le jeu de Nim est gagnant
- Pour le premier qui joue si au départ le pion est sur une case rouge ;
- Pour le second si au départ le pion est sur une case verte.
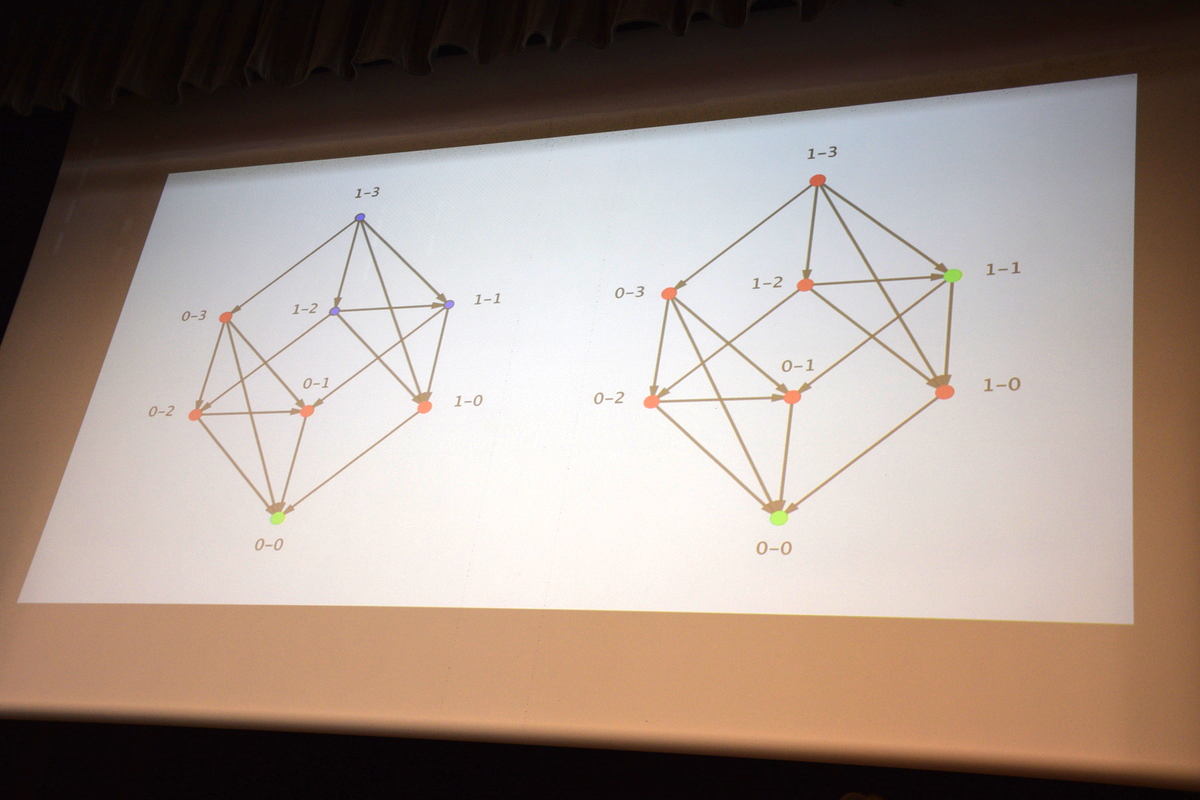
Voici la stratégie gagnante, coloriée par des élèves de 3e :
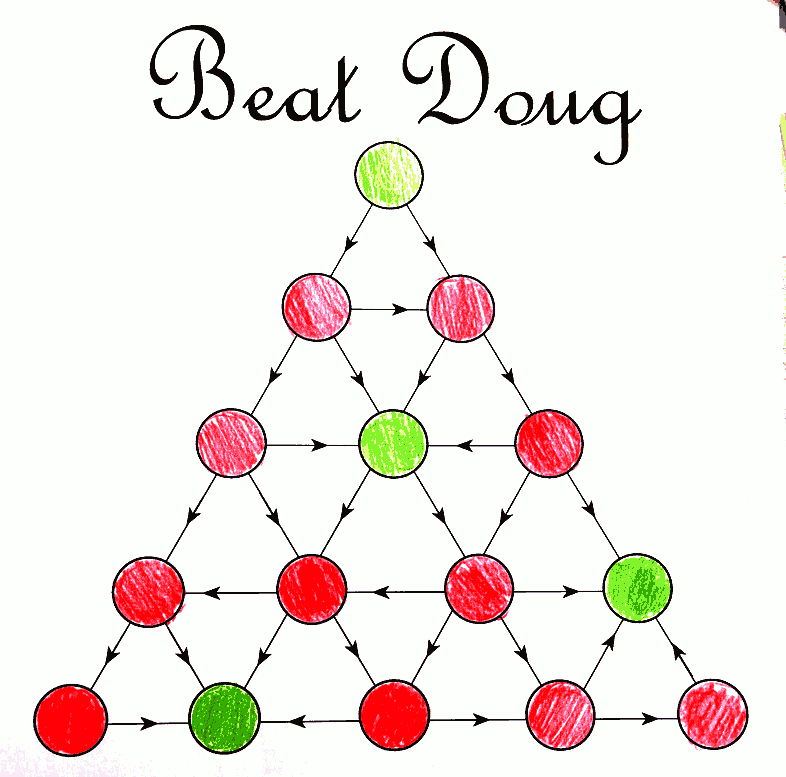
Le coloriage a été fait à partir des deux arrivées (les deux sommets verts du bas) en remontant progressivement avec ces règles :
- si un sommet mène à au moins un sommet vert, il est rouge ;
- à l’inverse si un sommet ne mène qu’à des sommets rouges il est vert.
Craig
Le même coloriage qu’avec Doug, effectué par des élèves de 6e, mène à une impasse :
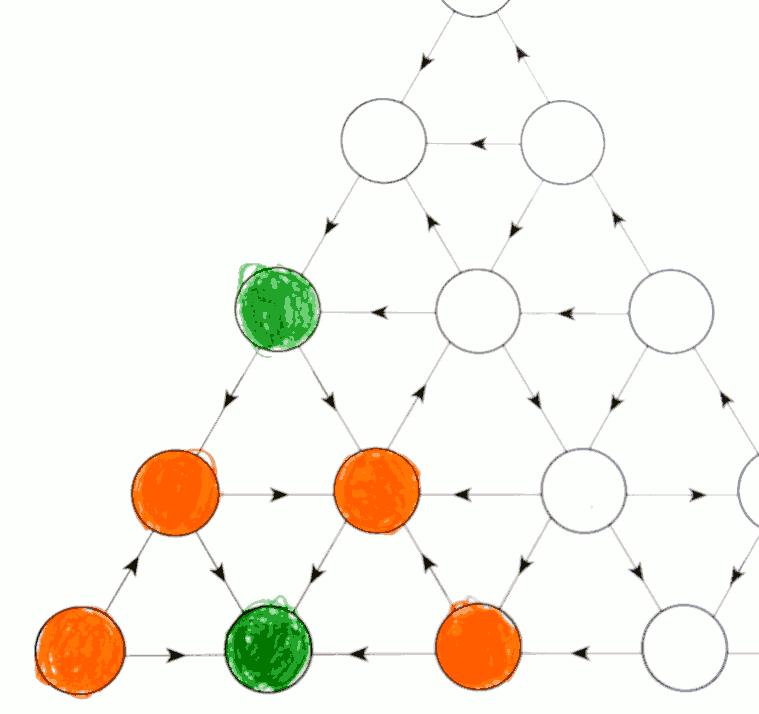
Les sommets à droite ne peuvent être coloriés car chacun mène à un sommet blanc qu’il faudrait colorier d’abord, ce qui est impossible puisque celui-ci mène à un sommet blanc etc.
En fait les élèves de 6e n’ont pas vu que les sommets en haut pouvaient être coloriés :
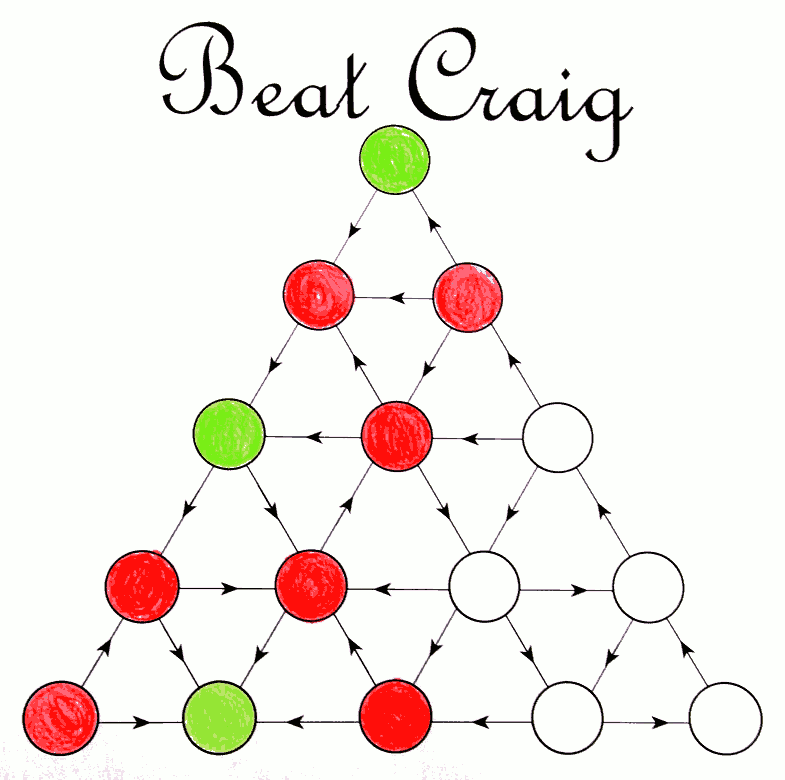
Ce coloriage a été effectué par des élèves de 3e. La stratégie gagnante consiste à mener le pion à un sommet vert, ce qui revient à éviter la zone blanche avec les cycles : Cela reviendrait à mener une partie nulle par répétition des situations du jeu.
Nim
Michèle Artigue utilise GeoGebra pour colorier les sommets du graphe d’un jeu de Nim ; elle garde les couleurs rouge et verte pour coder la stratégie gagnante (conférence d’ouverture du congrès M.e.J) :
Sprouts
Le jeu de Sprouts est de prise en mains très rapide mais se révèle vite addictif. Sa pratique révèle des erreurs de vision (ou de comptage) des arêtes de certains sommets et amène des débats sur qui a perdu, dont il émane un mouvement vers l’abstraction.
D’autres photos sont visibles sur IdM
On propose l’habillage suivant du jeu :
Le jeu se joue dans un pays où il y a, au début du jeu, des villes isolées. Chacun son tour va construire une route joignant deux villes (ou une ville à elle-même), mais
~ D'aucune ville, ne doivent partir plus de 3 routes.
~ Chaque fois qu'on construit une route, on construit une nouvelle ville sur cette route.
~ On ne peut pas construire de croisements entre deux routes.
Le premier qui ne peut plus construire de route en respectant ces contraintes, a perdu.De plus, on joue au tableau, ce qui facilite considérablement la gestion des joueurs.
Gaston-Crochet
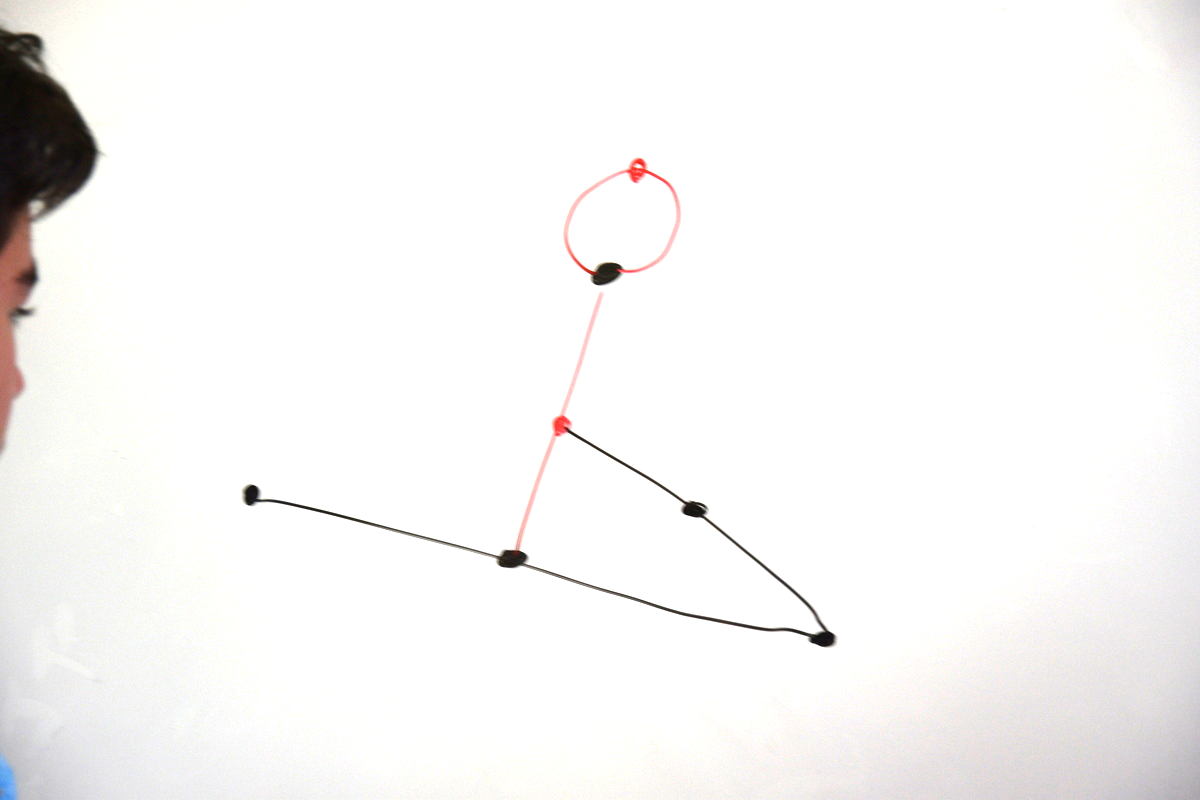
Voici un coup de jeu :
Le joueur part d’une ville
et trace une route vers une autre ville
puis ajoute une ville sur la route nouvellement construite :
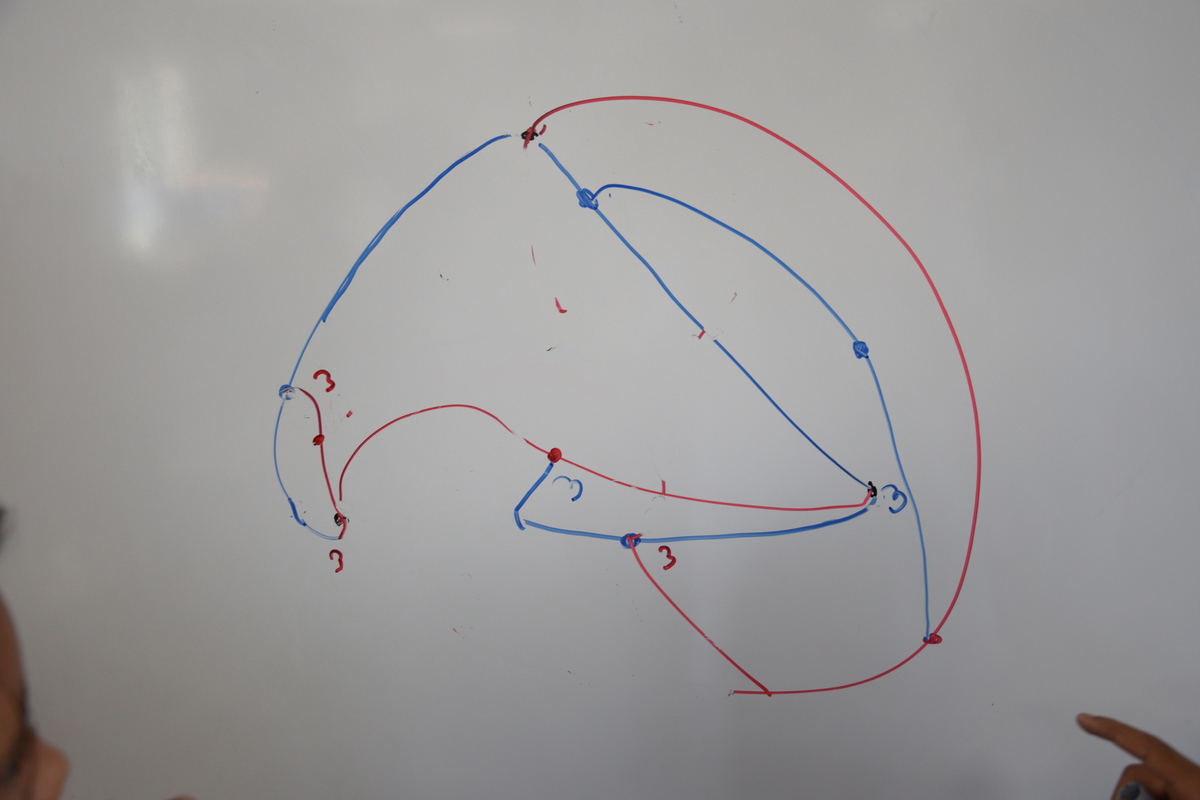
Voici le troisième coup d’un jeu : La route noire en cours de construction fait suite à deux routes, une noire et une rouge (c’est donc Noir qui a commencé le jeu) :
Le geste qu’on voit est la construction de la ville noire au milieu de la route noire.
Voici la riposte de Rouge :
Noir essaye alors de construire un coup illégal :
En effet la ville de départ de cette route non autorisée est de degré 3 : Il en part déjà 3 routes. Noir essaye d’en construire une quatrième, ce qui est interdit par la règle du jeu.
Ici le jeu se termine sur un cœur :
L’enthousiasme des joueurs amène parfois à tenter des parties plus longues, sur de grands nuages de points :
L’inconvénient est qu’on ne voit pas bien que certains coups interdits ont été joués :
Les élèves ont alors choisi de marquer d’une croix les villes terminées (dont déjà 3 routes sont issues) :
Mais comme on le voit, cette technique n’empêche pas de quand même créer un sommet de degré 4 (probablement parce que la joueuse avait oublié de marquer celui-ci d’une croix, quand elle l’a joué.
Voici ce que font certains élèves au lieu d’aller en récréation :
Constatant que la partie est terminée, l’un d’eux va d’ailleurs poser la question :
Mais pourquoi n’arrive-t-on pas à arrêter de jouer ?
La réponse à cette question n’est pas encore connue à ce jour.
400
Le fait de jouer à Sprouts au tableau blanc présente deux avantages sur la version papier-crayons :
- Le jeu attire le regard et donc les joueurs, de loin.
- Il est possible à l’animateur d’expliquer rapidement la règle du jeu à plusieurs élèves, dont l’un.e apprend en jouant contre l’animateur, ce qui libère rapidement l’animateur pour une autre activité, les joueurs étant rapidement autonomes sur Sprouts.
Comme la salle de l’école Louis-Clerc Fontaine réservée aux jeux d’intérieur était équipée d’un tableau blanc, l’activité a donc été refaite à l’école.
De façon générale les enfants se révèlent plus enclins que les adolescents à la prise d’initiative. Ils ne cherchant par exemple pas systématiquement la connexité du graphe :
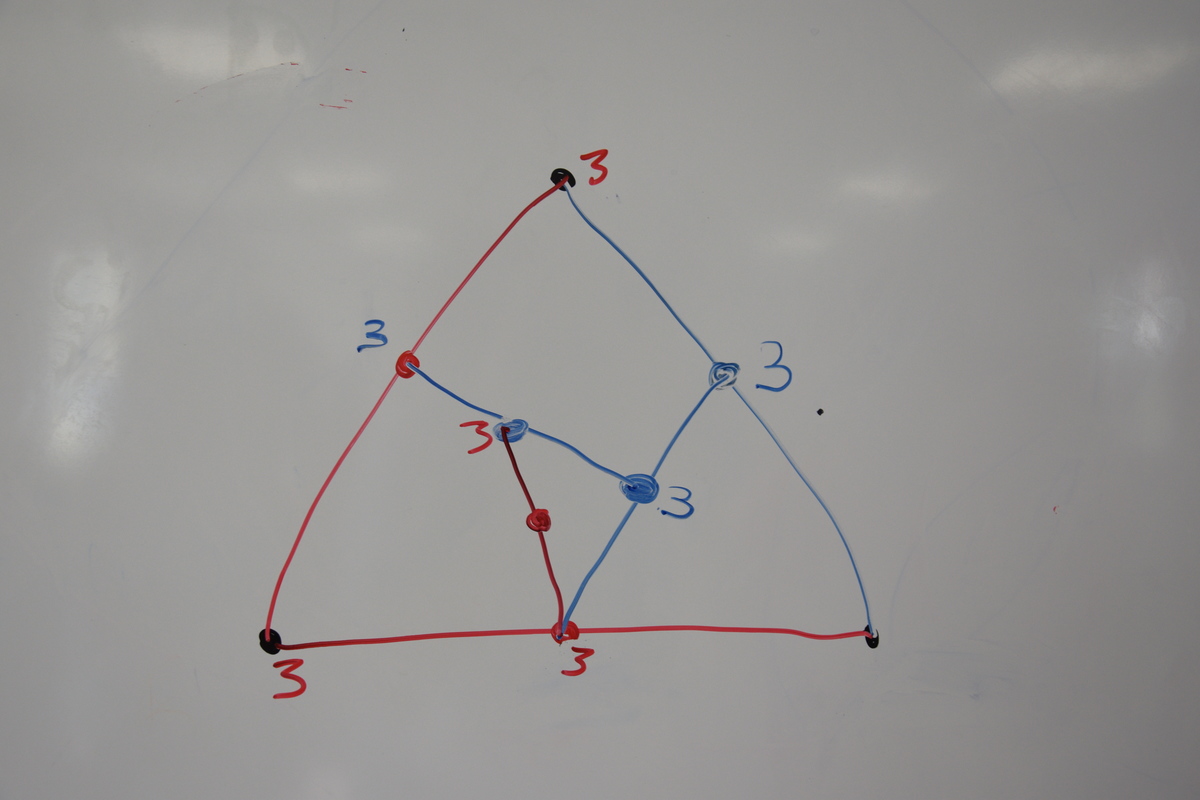
Chaque fois qu’aucune route ne peut partir d’une ville (parce qu’il y a déjà 3 routes), le nombre 3 est écrit à côté de la ville sur la carte routière :
Ci-dessus on voit immédiatement grâce à cet artifice que la partie est terminée : Il n’y a que deux villes non encore marquées, et l’une des deux est à l’intérieur d’un rectangle, l’autre à l’extérieur de ce rectangle, il n’est donc pas possible de relier ces villes par une route sans que cette route croise une autre route.
Le tracé n’est pas toujours sûr. Il y a des routes sinueuses
voire des virages à angle droit :
D’autres virages semblent répondre à un souhait de faire un réseau routier en Y sur la ville d’arrivée :
Sprouts peut-il amener à la découverte du triangle des milieux ?
Il a fallu moins d’une minute pour jouer cette partie :
Sprouts est donc adapté aux enfants ayant du mal à se concentrer longtemps, d’autant que l’animateur est libéré des explications des règles du jeu, par exemple pour gérer les cas particuliers.
Une fois qu’un joueur a été formé, il affronte un autre joueur, puis le gagnant affronte un nouveau joueur, et ainsi de suite, sous le regard des futurs joueurs et largement en autonomie. L’animateur doit de temps en temps rappeler les règles du jeu au cas où elles auraient mal été transmises d’élève à élève.
M.e.J.
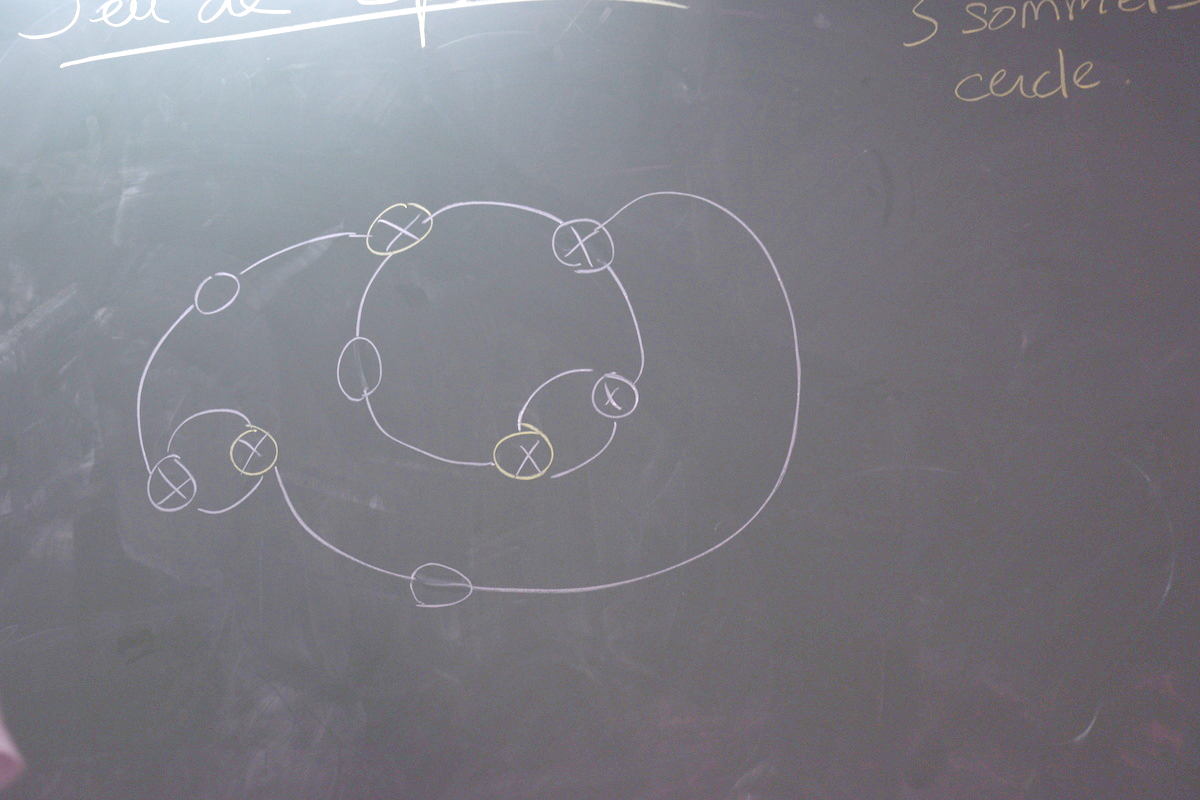
Au congrès M.e.J. on disposait d’un tableau noir et de craies. Mais le principe était similaire, avec une amélioration suggérée par un étudiant en L3 : Représenter les villes par des cercles et barrer ceux-ci d’une croix lorsque le réseau routier de la ville est saturé (3 routes issues de la ville).
Pour le tracé de la route, il y a deux techniques :
- Interrompre celui-ci pour tracer la ville, puis reprendre le tracé de la route depuis la ville :
- ou construire complètement la route, puis en détruire une partie (vive la craie !) pour y placer la ville :
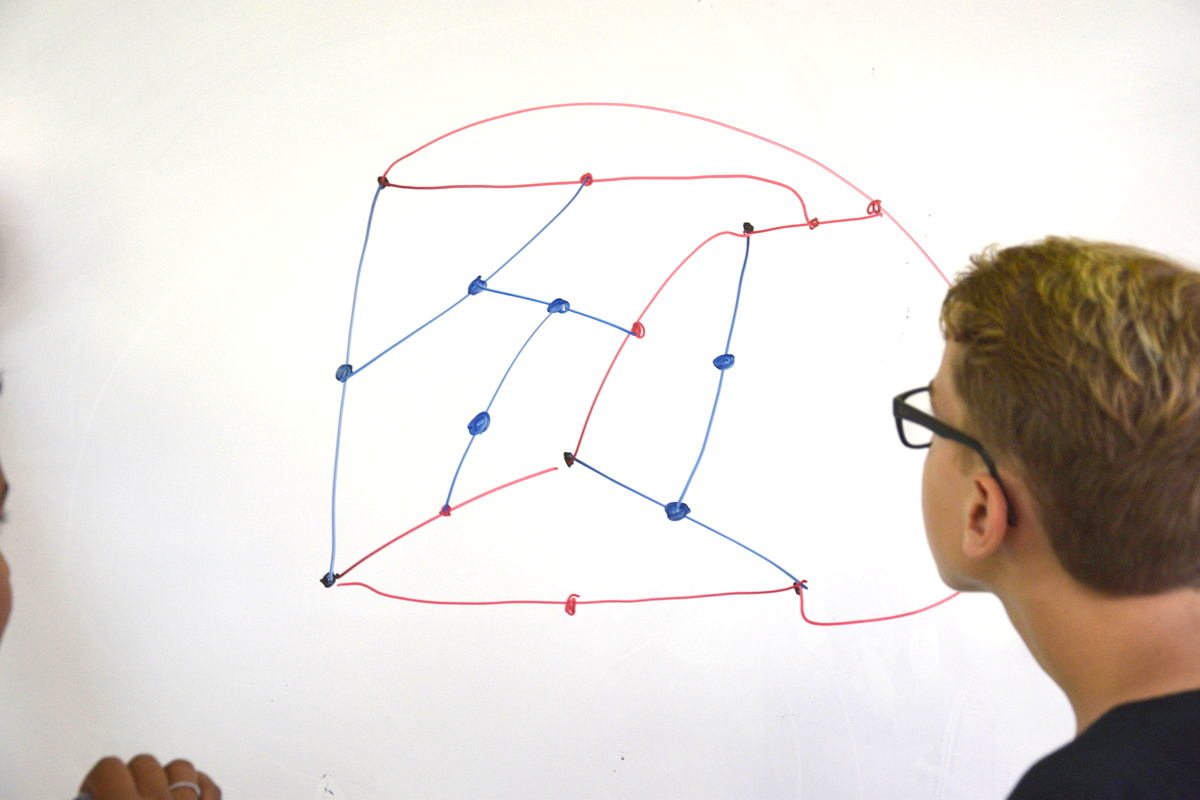
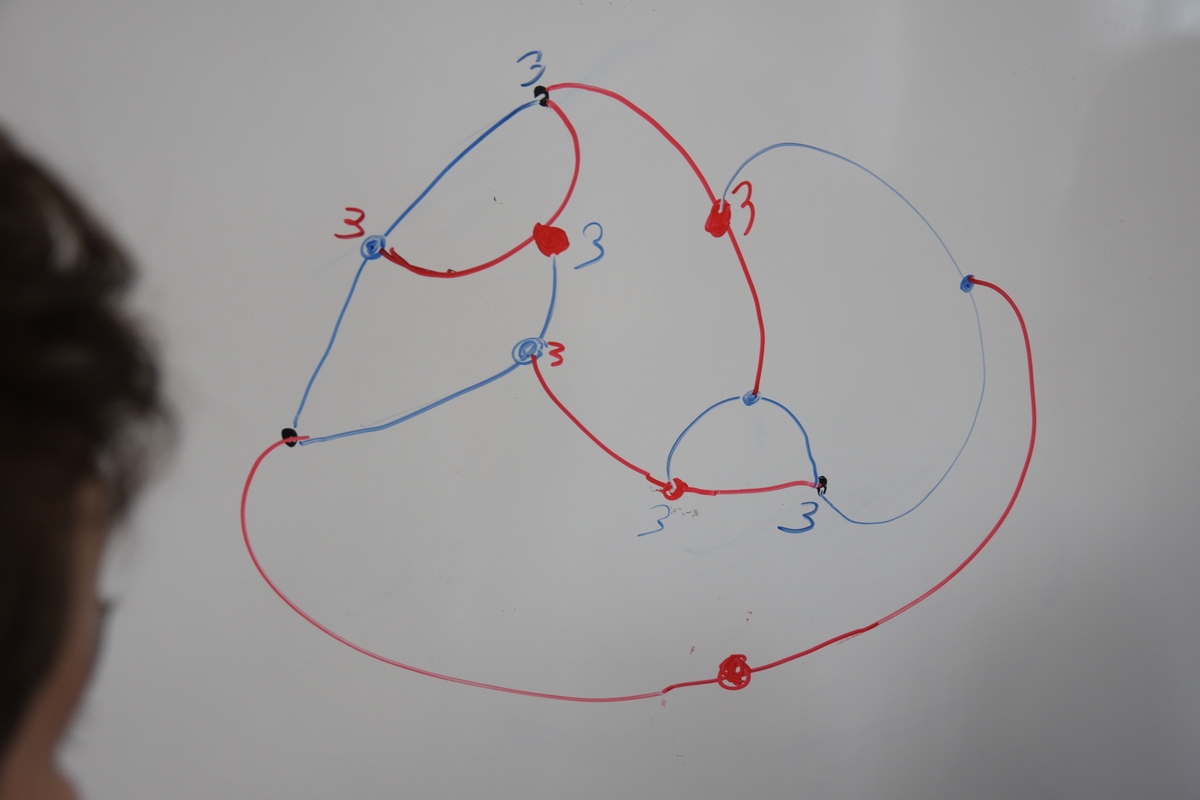
Certaines joueuses sont allées loin dans la complexité apparente du réseau routier :
D’autres ont inventé une version à 3 joueurs [5] :
Des élèves de 5e [6] ont décidé de varier l’aspect des villes (en coloriant plutôt que barrer celles-ci) :
Le jeu de Sprouts a bénéficié d’un tel succès qu’un article sur Images des Maths lui a été consacré.
Congrès MATh.en.JEANS
Le vendredi 29 mars l’amphi bioclimatique a accueilli plein de beau monde :
(de gauche à droite : Le proviseur du lycée de Bellepierre, le représentant du conseil départemental, le Recteur, le président de l’université, la vice-présidente de l’université, la présidente de M.e.J. et Marion Le Gonidec)
Mais que venaient-ils tous faire là ? Ils démarraient le congrès de M.e.J. pardi !
conférences
Le congrès, ça a été aussi des conférences. On y ajoute celles menées dans le cadre de la semaine des maths, et menées avant le démarrage du congrès.
Descartes
Le mercredi, avant l’ouverture du congrès, a eu lieu une première conférence, dont le thème est l’histoire des maths : Dominique Tournès a présenté de nombreuses activités que l’on peut mener notamment avec la géométrie dynamique, sur des exemples traités par Descartes.
Voici le conférencier, à une autre occasion, en compagnie de Michèle Artigue :
Hanoï
Puis ce fut la première conférence de Benoït Rittaud, portant sur la tour d’Hanoï et présentant des recherches en cours sur l’algorithmique de ce jeu et ses généralisations.
Des questions intéressantes peuvent mener à des recherches innovantes. Un exemple est « comment faire pour résoudre la tour d’Hanoï en maximisant le nombre de mouvements ? »
On remarque que les études sur la tour d’Hanoï font usage de la numération.
Jeux
La conférence d’ouverture a été menée par nulle autre que Michèle Artigue. Elle portait sur l’histoire des jeux combinatoires et on y a joué à Nim. Sur scène :
Michèle est toujours la bienvenue à La Réunion :
Nœuds
La conférence de Cyrille Ospell portait sur la topologie, et plus particulièrement sur la théorie des nœuds.
On remarque que la théorie des nœuds fait usage d’un outil créé par Conway qui fut la vedette de la conférence de clôture.
Sowing
La conférence de clôture fut un hommage rendu à John Conway, expliquant comment celui-ci a construit les réels (ainsi que bien d’autres nombres au passage) par les jeux combinatoires. Ce sont des jeux de Sowing qui ont été choisis pour illustrer par des exemples comment on construit les entiers relatifs, puis les fractions dyadiques, puis les nombres réels et hyperréels (infinitésimaux par exemple) et des jeux comme ceux de Nim qui ne sont pas des nombres.
Voici le diaporama de la conférence :
PACOM
L’atelier PACOM a été sollicité pour animer plusieurs activités durant le congrès. Comme le principe est de faire des maths à ciel ouvert, la météo a un peu compliqué la tâche.
Outre des ateliers déjà expérimentés (zistoir maron, un intégramme) il y a eu deux nouveautés cette année :
- Les polygones
- Le flocon de Von Koch
Polygones
Des modèles de polygones en métal ont été amenés, et les participants avaient pour rôle de les identifier puis les reproduire à plus grande échelle :

Intégramme
Ici pour savoir qui est marié à qui et habite où, il faut bouger :

IREM
D’autres animations IREM étaient présentes au congrès M.e.J. ; on a déjà évoqué les graphes, Sowing, le binaire et l’abaque à jetons. Voici les autres activités hors Pacom :
Cesar
On a beaucoup déchiffré au Moufia :

Casse-têtes
Parmi les casse-têtes, le tangram garde son succès :

Lors de la conférence d’ouverture, ce jeu avait été cité par Michèle Artigue. C’était intéressant de pouvoir y jouer après avoir entendu parler du jeu.




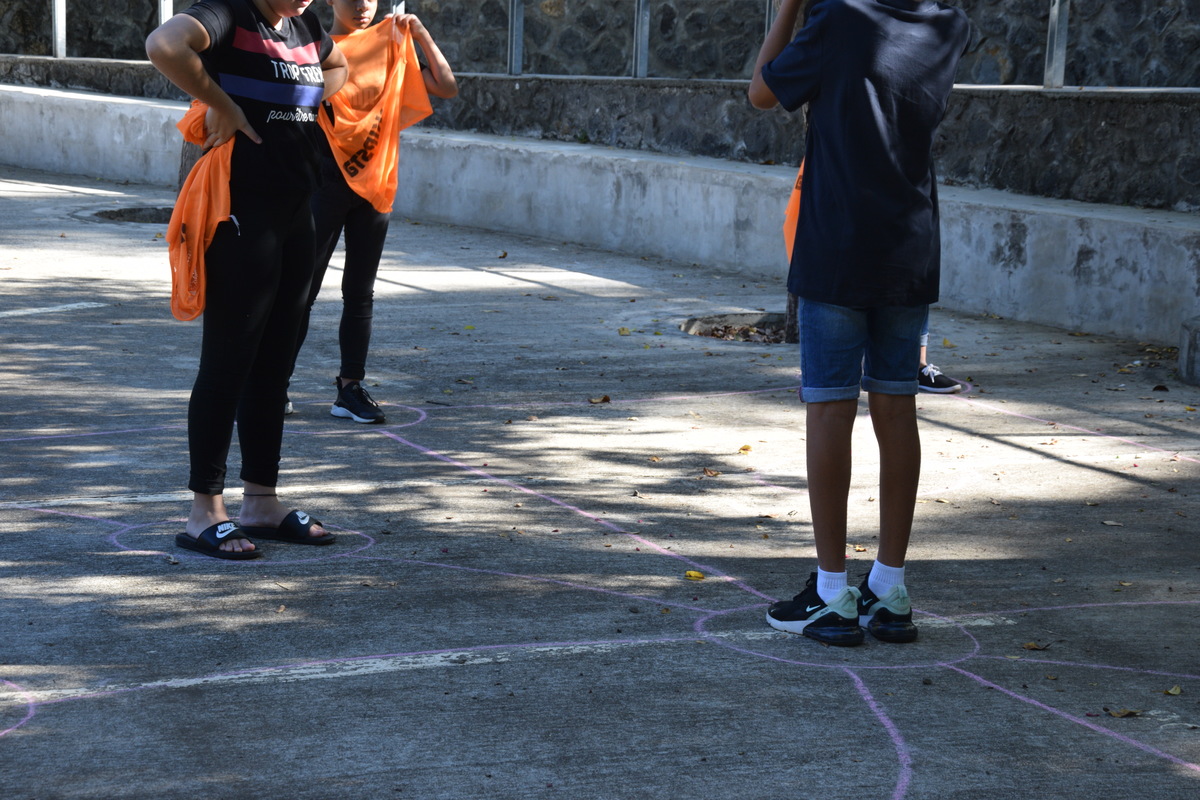

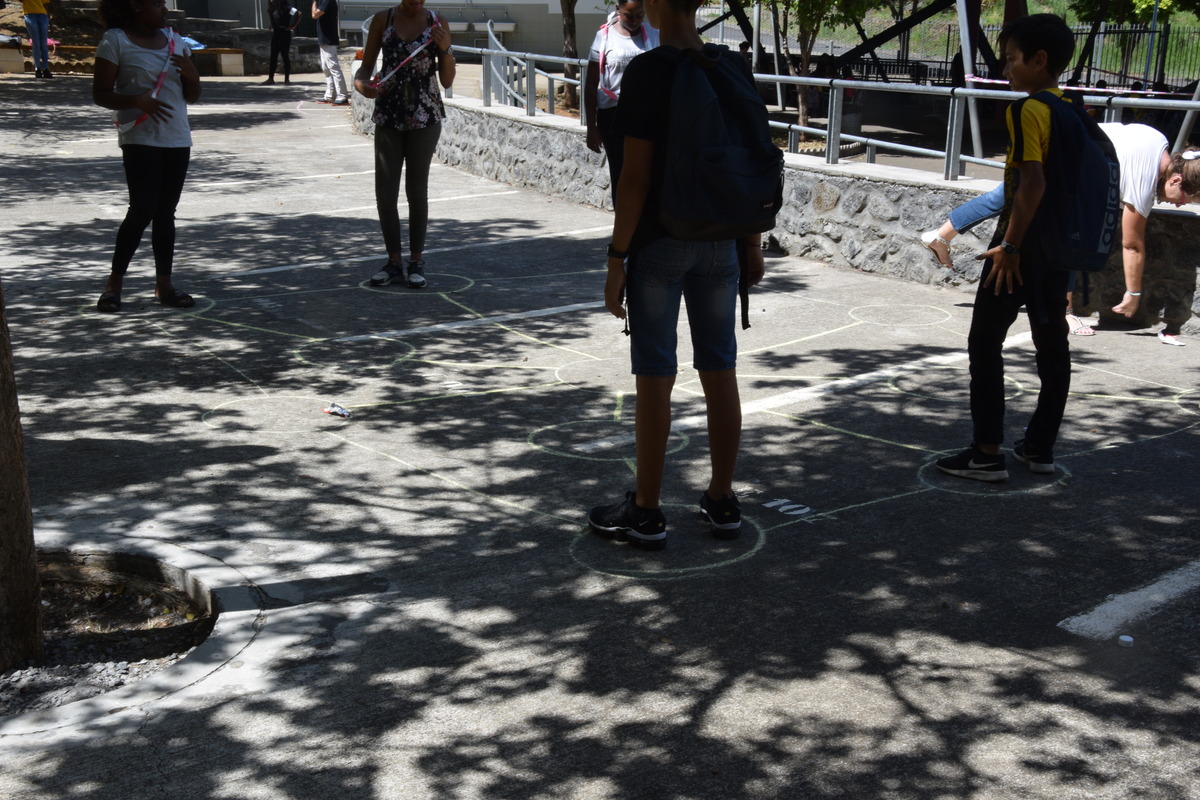






















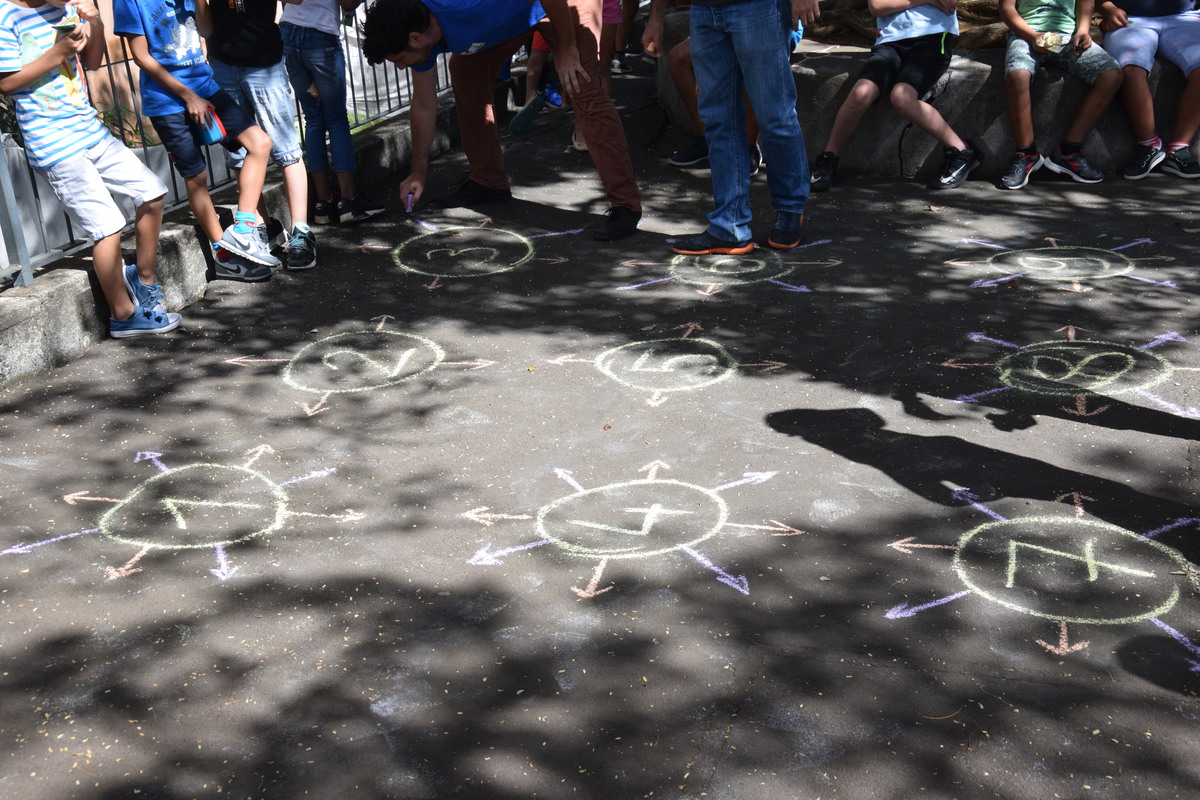
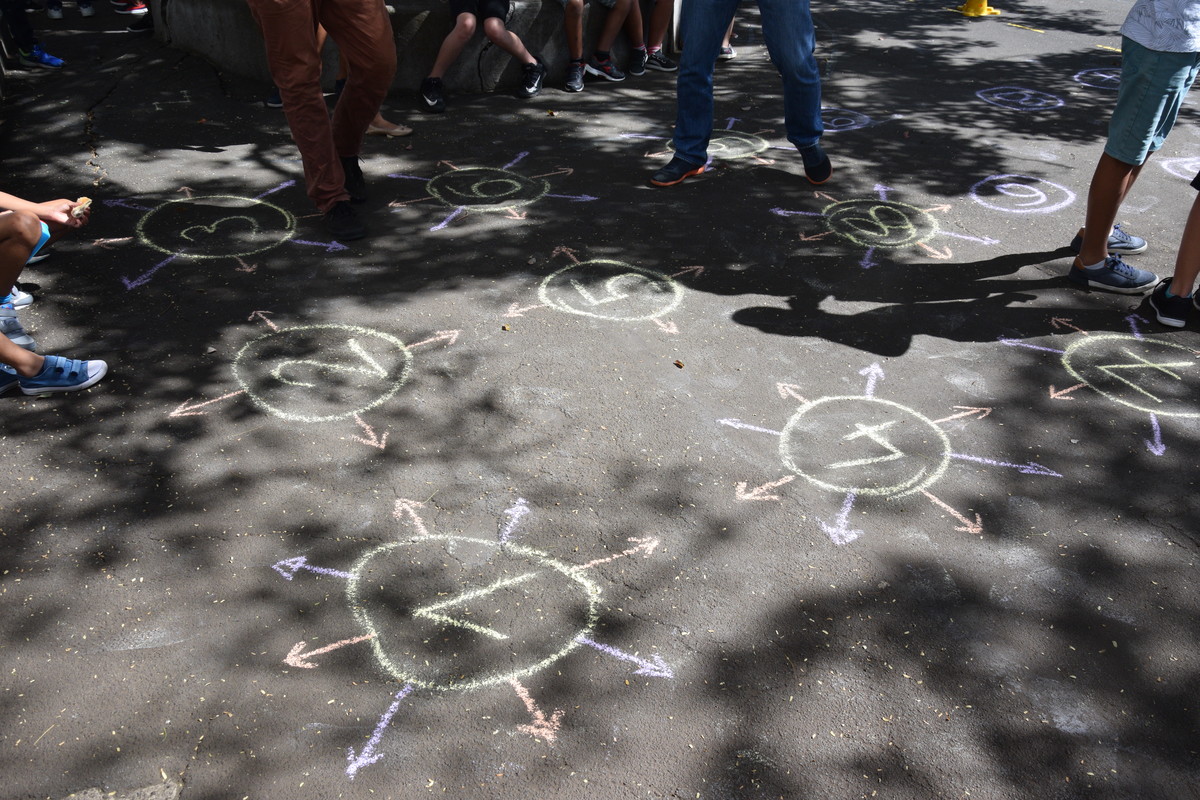


















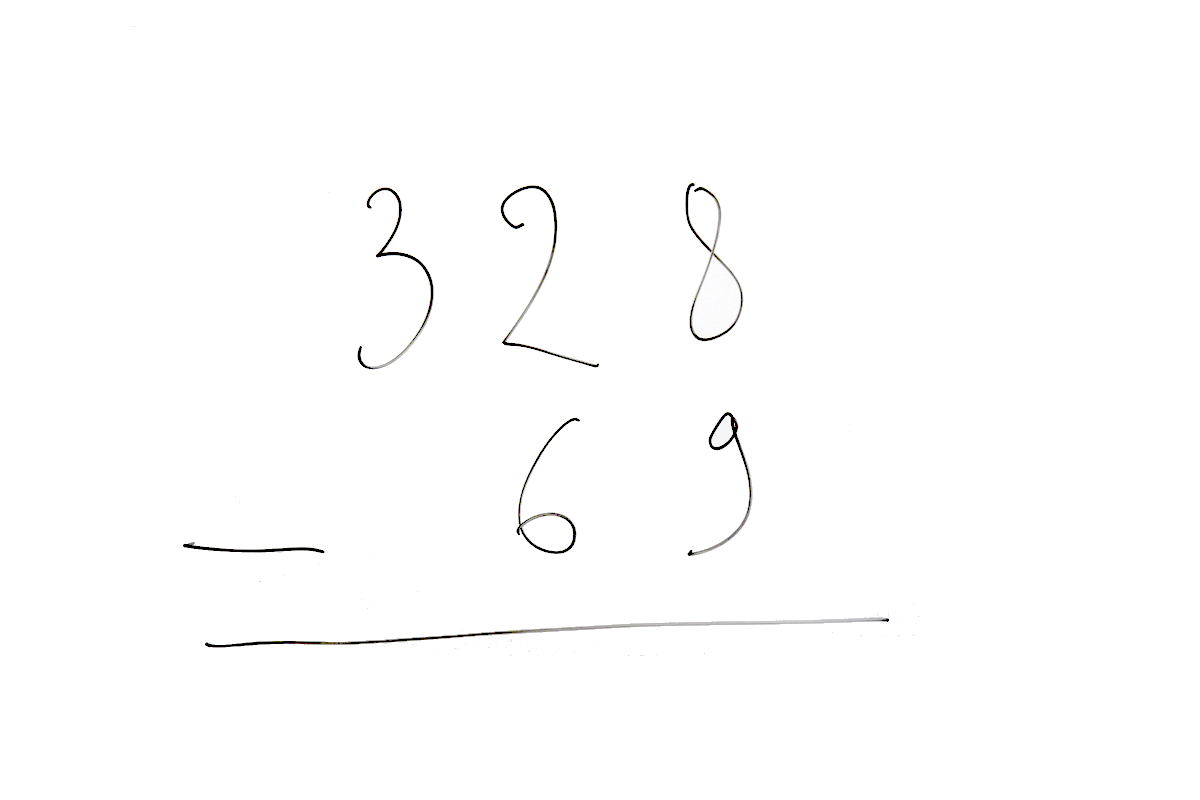






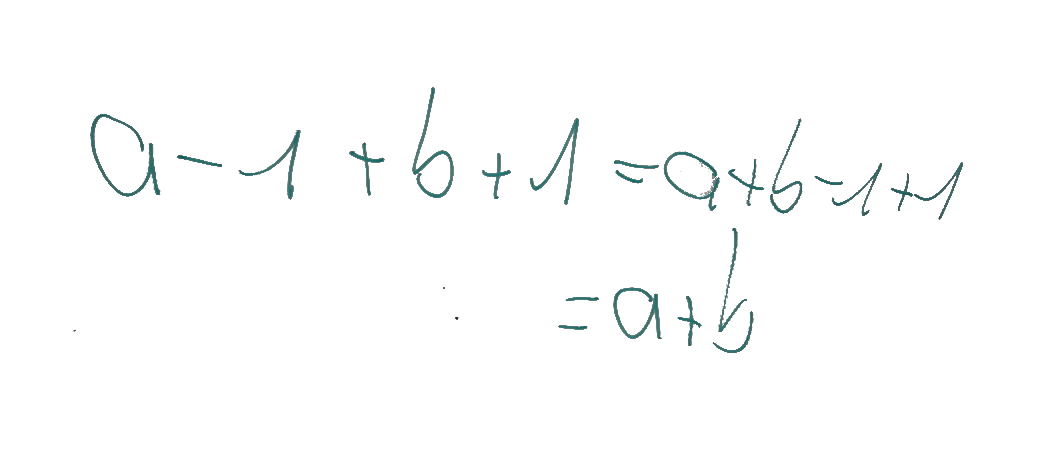

































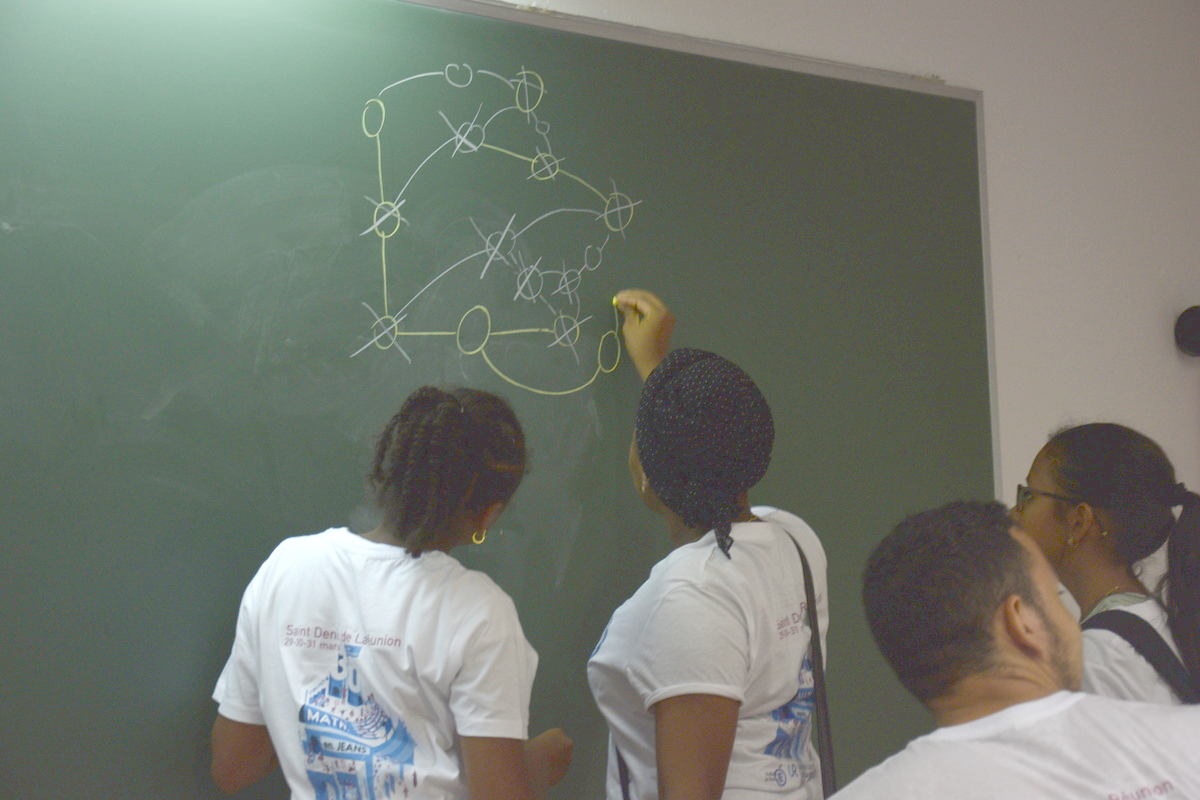
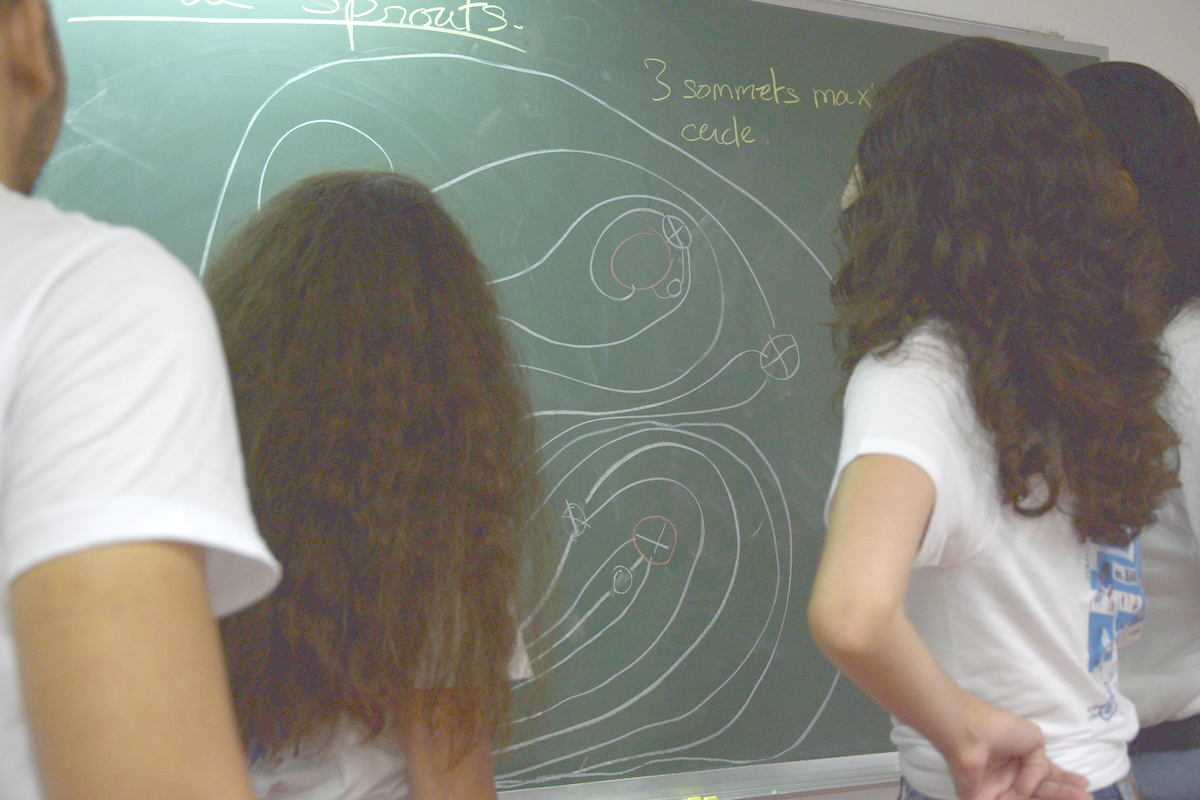
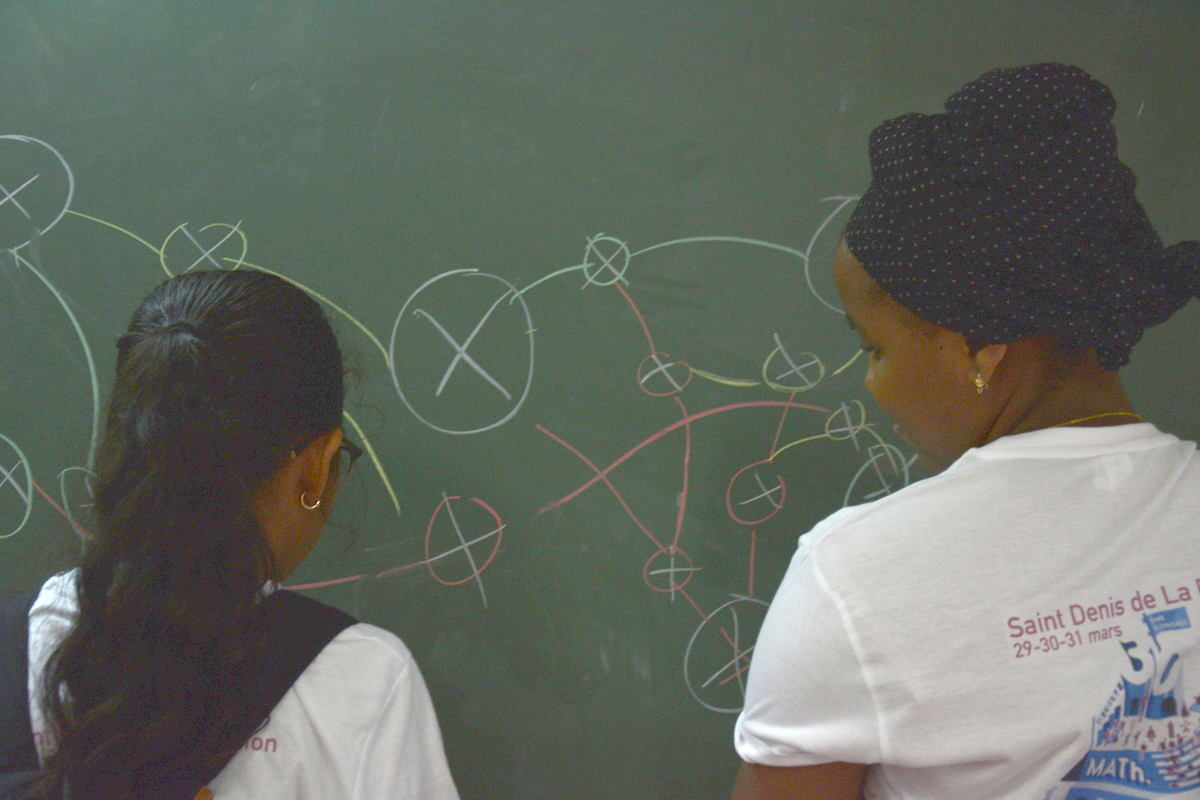

































Commentaires