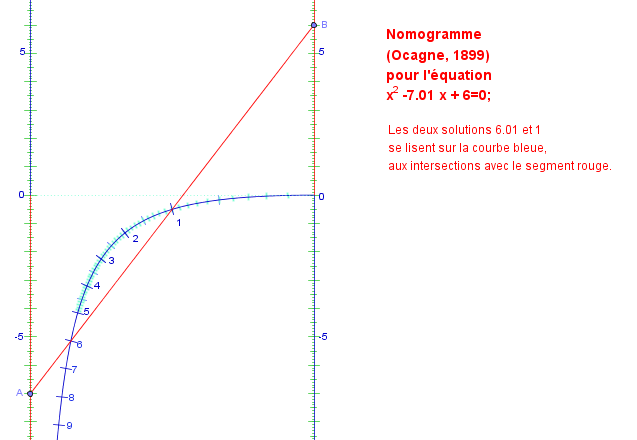
L’intersection de la droite passant par les points de coordonnées respectives $(0,p)$ et $(1,q)$ et de l’hyperbole d’équation $y=-\frac{(x-1)^2}{x}$ est formée des points d’abscisses respectives $\frac{1}{a+1}$ et $\frac{1}{b+1}$ si $a$ et $b$ sont les solutions de l’équation $x^2+px+q=0$. Donc pour peu que l’hyperbole soit graduée homographiquement, on a un nomogramme pour résoudre les équations du second degré :
La version pdf est téléchargeable au bas de l’article.
Elle a été créée en Asymptote.
Voici le code (assez différent de la version GeoGebra, qui quant à elle est basée sur l’outil "séquence") :
Pour par exemple résoudre l’équation $x^2-3x+2=0$, on repère la graduation -3 sur l’axe de gauche et la graduation 2 sur l’axe de droite, on tend un fil entre les deux points ainsi repérés, et la droite qu’on vient de matérialiser coupe l’hyperbole en deux points, dont les graduations donnent les solutions de l’équation.
Bien sûr si la droite ne croise pas l’hyperbole, c’est que le discriminant de l’équation est négatif.
Variante : troisième degré
Il suffit de remplacer l’hyperbole par la représentation graphique de la fonction $y=-\frac{(x-1)^3}{x^2}$ pour résoudre graphiquement les équations du troisième degré $x^3+px+q=0$. Sauf que maintenant l’équation a une troisième solution, négative, dont on lit l’opposé en menant une nouvelle droite à partir du point de coordonnées $(1,-q)$.
Voici le résultat :
La version pdf est téléchargeable au bas de cet article
Elle aussi a été faite par un programme Asymptote


Commentaires