Il y a essentiellement deux manières pour "deviner" ce que fait un algorithme :
- Repasser mentalement les étapes (ce qu’on peut faire à l’écrit)
- ou "traduire" l’algorithme dans un langage de programmation (ce qu’on peut faire à l’écrit aussi, mais à condition que la calculatrice soit autorisée).
C’est la deuxième méthode qui sera utilisée ici, puisqu’il s’agit d’un TP.
Exploration de l’algorithme
Voir la version algobox en ligne
2 N EST_DU_TYPE NOMBRE
3 P EST_DU_TYPE NOMBRE
4 I EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 LIRE N
7 P PREND_LA_VALEUR 1
8 POUR I ALLANT_DE 1 A N
9 DEBUT_POUR
10 P PREND_LA_VALEUR P*I
11 FIN_POUR
12 AFFICHER P
13 FIN_ALGORITHME
La traduction directe depuis le pseudocode vers JavaScript donne ceci (à part qu’il a fallu ajouter l’entrée (affectation de $N$) et la sortie (affichage de la valeur finale de $P$) :
var N=Input("Entrer un entier : ");
var P=1;
for(I=1;I<=N;I=I+1){
P=P*I;
}
Alert("Avec "+N+", le programme donne "+P);Ceci dit, il est plus confortable pour la suite d’écrire une fonction (au sens algorithmique du terme) qui sera réutilisable par la suite. Voici la fonction JavaScript [1] :
function algo(n){
var p=1;
for(i=1;i<=n;i=i+1){
p=p*i;
}
return(p)
}Avec ça, c’est facile d’écrire une boucle appelant la fonction algo(n) pour les valeurs consécutives de n :
function algo(n){
var p=1;
for(i=1;i<=n;i=i+1){
p=p*i;
}
return(p)
}
for(n=1;n<=20;n=n+1){
Println("|"+n+"|"+algo(n)+"|");
}Son exécution sous CaRMetal donne le tableau suivant [2] :
| n | p |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
La conjecture sur la nature de la fonction algo(n) est laissée au lecteur [3]
Les suites
On appelle $u$, $v$ et $e$ les termes courants des suites $u_n$, $v_n$ et $e_n$ (ce sont des variables mises à jour dans la boucle sur $n$). Comme $u_n$ est une somme, on effectue une nouvelle boucle sur $k$, dans laquelle on additionne la valeur courante de la somme $u$ et de $\frac{1}{k !}$ (en effet, $u_k=u_{k-1}+\frac{1}{k !}$) :
/*Programme tp 60a
*/
function fact(n){
var p=1;
for(i=1;i<=n;i=i+1){
p=p*i;
}
return(p)
}
var u,v,e;
for(n=1;n<=20;n=n+1){
u=0;
for(k=0;k<=n;k=k+1){
u=u+1/fact(k);
}
v=u+1/n/fact(n);
e=v-u;
Println("|"+n+"|"+u+"|"+v+"|"+e+"|");
}(On remarque que, par définition de $v_n$, $e_n=\frac{1}{n \cdot n !}$ ce qui rend l’exercice quelque peu circulaire.)
L’exécution du script sous CaRMetal produit le tableau suivant :
| n | $u_n$ | $v_n$ | $e_n$ |
| 1 | 2 | 3 | 1 |
| 2 | 2.5 | 2.75 | 0.25 |
| 3 | 2.6666666666666665 | 2.722222222222222 | 0.05555555555555536 |
| 4 | 2.708333333333333 | 2.7187499999999996 | 0.010416666666666519 |
| 5 | 2.7166666666666663 | 2.718333333333333 | 0.0016666666666664831 |
| 6 | 2.7180555555555554 | 2.718287037037037 | 0.0002314814814816657 |
| 7 | 2.7182539682539684 | 2.71828231292517 | 0.000028344671201718796 |
| 8 | 2.71827876984127 | 2.7182818700396827 | 0.000003100198412653299 |
| 9 | 2.7182815255731922 | 2.718281831765628 | 3.0619243585050526e-7 |
| 10 | 2.7182818011463845 | 2.7182818287037036 | 2.755731909331871e-8 |
| 11 | 2.718281826198493 | 2.7182818284759573 | 2.277464439259802e-9 |
| 12 | 2.7182818282861687 | 2.7182818284601415 | 1.7397283613718173e-10 |
| 13 | 2.7182818284467594 | 2.7182818284591126 | 1.2353229550399192e-11 |
| 14 | 2.71828182845823 | 2.7182818284590495 | 8.193445921733655e-13 |
| 15 | 2.718281828458995 | 2.718281828459046 | 5.10702591327572e-14 |
| 16 | 2.718281828459043 | 2.718281828459046 | 3.1086244689504383e-15 |
| 17 | 2.7182818284590455 | 2.7182818284590455 | 0 |
| 18 | 2.7182818284590455 | 2.7182818284590455 | 0 |
| 19 | 2.7182818284590455 | 2.7182818284590455 | 0 |
| 20 | 2.7182818284590455 | 2.7182818284590455 | 0 |
Pour mieux voir ce qui se passe, on peut légèrement modifier le script ci-dessus pour, au lieu d’afficher les valeurs numériques de $u$, $v$ et $e$, les représenter par des nuages de points ($u_n$ en bleu, $v_n$ en rouge et $e_n$ en vert) : Le script ci-dessous
/*Programme tp 60b
*/
function fact(n){
var p=1;
for(i=1;i<=n;i=i+1){
p=p*i;
}
return(p)
}
var u,v,e;
for(n=1;n<=20;n=n+1){
u=0;
for(k=0;k<=n;k=k+1){
u=u+1/fact(k);
}
v=u+1/n/fact(n);
e=v-u;
a=Point(n,u);
SetColor(a,"blue");
SetPointType(a,"dcross");
b=Point(n,v);
SetColor(b,"red");
SetPointType(b,"cross");
c=Point(n,e);
SetColor(c,"green");
SetPointType(c,"circle");
}produit l’image suivante :
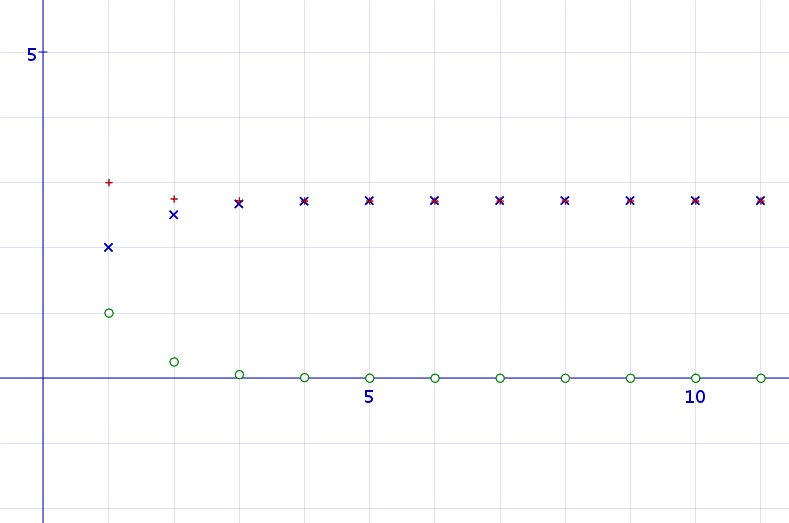
Il y en assez pour conjecturer la convergence de $e_n$ et l’adjacence de $u_n$ et $v_n$.


Commentaires