Une constatation préliminaire : environ la moitié de ces bacheliers (essentiellement STL) n’ont jamais vu GeoGebra de leur vie [1]...
Vidéoprojeter l’ordinateur d’un des étudiants aide grandement les autres, et les oblige à rester concentrés pendant toute l’heure.
Nuage de points
La création d’un nuage de points est rapide grâce au nommage automatique de GeoGebra. Cela met les étudiants en confiance (ils voient que GeoGebra est facile à utiliser et ne se découragent pas d’emblée) et permet de gagner du temps pour la suite, qui est plus longue. Pour faire le tout en une heure, il vaut mieux prendre 4 points ; mais par pure ambition, 5 points A, B, C, D et E ont été construits.
Pour construire la droite de régression obtenue par la méthode des moindres carrés, il suffit de sélectionner l’outil idoine (menu des droites construites), puis d’encercler les points avec un rectangle de sélection tracé à la souris :
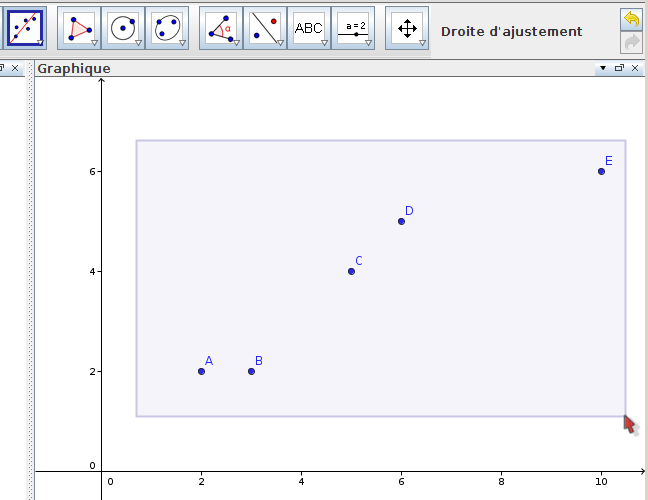
Après ça, il faut quand même faire un clic droit sur la droite [2] pour mettre son équation sous la forme y=ax+b, et en profiter pour la colorier en rouge. En examinant les propriétés de la droite, on découvre la syntaxe des listes :
{A,B,C,D,E}qui servira par la suite.
Point moyen
Encore un raccourci utile : la possibilité d’additionner des points pour avoir directement le point moyen :

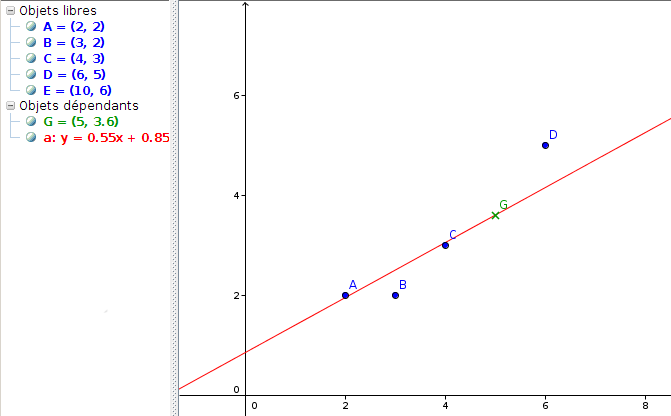
En mettant le point moyen G en vert (et en lui donnant une autre forme) pour le distinguer des points du nuage, on peut maintenant découvrir expérimentalement la propriété suivante :
La droite de régression obtenue par la méthode des moindres carrés passe toujours par le point moyen du nuage.
Moindres carrés
Ensuite, pour montrer d’où vient ce nom bizarre [3], on construit une autre droite (FH) en pointillés verts ci-dessous :
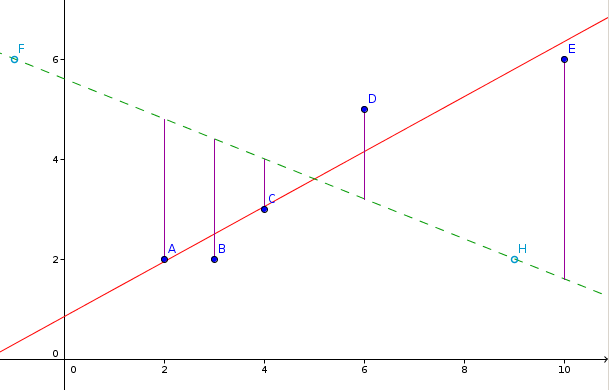
Les points A, B, C, D et E ont été projetés sur la droite (FH) parallèlement à l’axe des ordonnées avec l’algorithme suivant :
- On a tracé les droites verticales passant par A, B, C, D et E avec l’outil « parallèle » (en cliquant sur un des points puis l’axe des ordonnées) ; c’est là que les plus lents ou les plus maladroits commencent à ramer un peu ;
- puis on a construit les intersections de ces droites verticales avec la droite (FH) ;
- puis on a caché les droites verticales (en cliquant sur le bouton à gauche de leur nom dans la fenêtre algèbre) ;
- puis on a construit les segments en mauve, que GeoGebra a nommés h, i, j, k et l ;
- enfin on a caché les points d’intersection.
Pour éviter de surcharger la figure (et par manque de temps), on n’a pas tracé les carrés assis sur ces segments mauves, dont on cherche à minimiser la somme des aires. On s’est contenté de calculer algébriquement cette somme avec
sdc=h*h+i*i+j*j+k*k+l*lL’abondance d’objets déjà construits rend malaisée la lecture de la fenêtre algèbre, et l’affichage de la somme des carrés a été introduit dans la figure sous la forme d’un texte dynamique, où la variable sdc est concaténée au texte par un « + » :
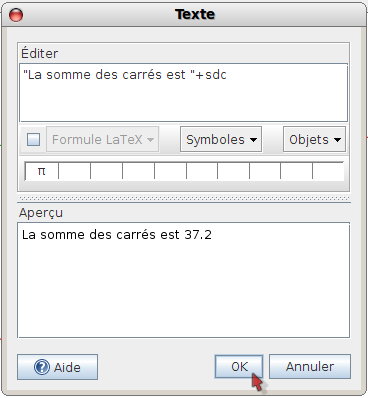
C’est cette étape qui a le plus épaté les étudiants. L’effet est assez puissant, il faut le reconnaître :

Environ les deux tiers des étudiants ont réussi à minimiser la somme des carrés, et donc à découvrir que pour atteindre ce minimum, il fallait placer F et H sur la droite rouge. D’où son nom :
La droite des moindres carrés est celle qui minimise la somme des carrés des distances verticales (c’est-à-dire les longueurs des segments verticaux) des points à la droite.
Covariance
Pour la suite (qu’un seul groupe a eu le temps de faire en entier), on peut rendre invisible tout ce qui a été construit à l’onglet précédent. La covariance a été définie dans le cours.
La trousse d’outils statistiques de GeoGebra est assez étendue pour inclure la covariance, et en plus, avec le raccourci de regrouper les x et les y comme coordonnées de points :

Sans trop chercher à comprendre ce qu’est exactement la covariance [5], on peut faire
c1=Covariance[{A,B,C,D,E}]
c2=Variance[{x(A),x(B),x(C),x(D),x(E)}]
c3=c1/c2puis colorier c3 en rouge et le comparer avec le coefficient directeur de la droite de régression pour découvrir expérimentalement la propriété suivante :
Le coefficient directeur de la droite de régression obtenue par la méthode des moindres carrés est le quotient de la covariance des abscisses et des ordonnées, par la variance des abscisses.
Ce qui fournit un algorithme permettant de calculer l’équation de la droite [6]
Corrélation
Dans le cours, le coefficient de corrélation a été défini comme le quotient de de la covariance par le produit des écarts-type :

Mais GeoGebra a aussi un coefficient de corrélation, et peut même calculer directement celui des abscisses et ordonnées d’un nuage de points :

La fin de l’activité a donc consisté à comparer ces deux nombres, et à évaluer l’impact de l’alignement des points sur la valeur du coefficient de corrélation :
Points très mal alignés :
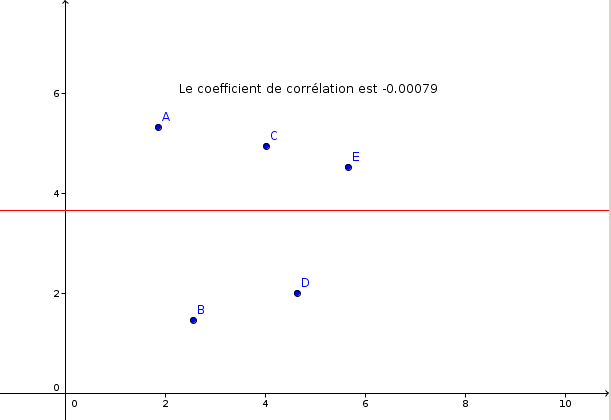
Points plutôt mal alignés :
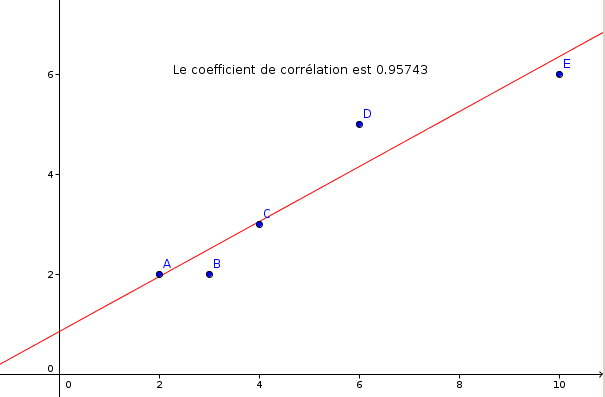
Points bien alignés :

Points bien alignés mais... :
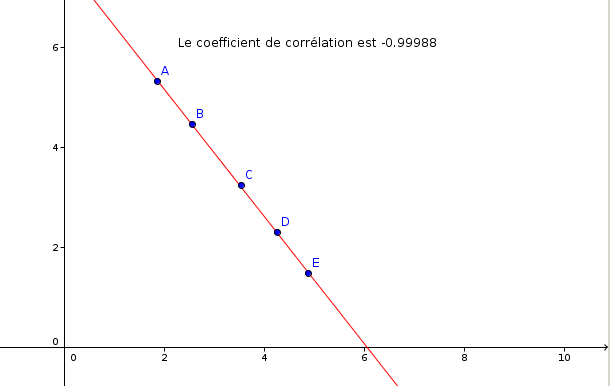
Hacking
Tout ceci amène assez naturellement la question de savoir comment GeoGebra calcule les coefficients en question, et notamment si c’est avec les formules du cours. Or, GeoGebra étant un logiciel libre, il est tout-à-fait possible de répondre à cette question, tout simplement en consultant son code source [7]
Voici donc la manière dont GeoGebra calcule l’équation de la droite de régression (on constate le calcul simultané des moyennes et de la variance des x et de la covariance, dont les numérateurs sont nommés respectivement sigmax, sigmay, sigmaxy et sigmaxx) :
public final void compute() {
double sigmax = 0;
double sigmay = 0;
double sigmaxx = 0;
// double sigmayy=0; not needed
double sigmaxy = 0;
for (int i = 0; i < size; i++) {
GeoElement geo = geoList.get(i);
if (geo.isGeoPoint()) {
double xy[] = new double[2];
((GeoPoint) geo).getInhomCoords(xy);
double x = xy[0];
double y = xy[1];
sigmax += x;
sigmay += y;
sigmaxx += x * x;
sigmaxy += x * y;
// sigmayy+=y*y; not needed
} else {
g.setUndefined();
return;
}
}
// y on x regression line
// (y - sigmay / n) = (Sxx / Sxy)*(x - sigmax / n)
// rearranged to eliminate all divisions
g.x = size * sigmax * sigmay - size * size * sigmaxy;
g.y = size * size * sigmaxx - size * sigmax * sigmax;
g.z = size * sigmax * sigmaxy - size * sigmaxx * sigmay; // (g.x)x +
// (g.y)y +
// g.z = 0
}Si on fait abstraction du fait que l’équation de la droite est donnée sous forme homogène [8], l’équation de la droite de régression est bien établie à partir des deux informations suivantes :
- Son coefficient directeur est le quotient de la covariance par la variance des x (plus précisément, le quotient de leurs numérateurs ; en effet ils ont le même dénominateur) ;
- Elle passe par le point moyen.
Quant au calcul du coefficient de corrélation, lui aussi est fait d’après la définition du cours :
case STATS_PMCC:
result.setValue((sumxy*sizex-sumx*sumy)/Math.sqrt((sumxx*sizex-sumx*sumx)*(sumyy*sizex-sumy*sumy)));Michael Borcherds économise le calcul d’une racine carrée en utilisant le fait que le produit des écarts-type est la racine du produit des variances. Et il économise les divisions par le nombre de points du nuage en gardant les numérateurs au lieu des moyennes.


Commentaires