Dans un jeu de connexion, les joueurs essayent de relier des emplacements par des chemins, construits morceau par morceau. Ces jeux font donc travailler la vision, et plus particulièrement celle des lignes. Des jeux de connexion ont donc été testés par des élèves non lecteurs
Suivre une ligne du regard, n’est pas à la portée d’un enfant souffrant de certaines formes de « dyslexie ». Plus tard, ces élèves peuvent avoir du mal à chercher une information dans un tableau à double entrée, ou à viser un point d’après ses coordonnées : pour cela il faut suivre des parallèles (en fait ce sont plutôt des hypercycles, ce qui nécessite de savoir estimer des distances) à deux droites ce qui est encore plus difficile que suivre une seule parallèle.
Pourtant, une célèbre expérience de Hubel et Wiesel révèle que ce que notre cerveau perçoit, ce sont des lignes (plus ou moins contrastées, plus ou moins inclinées). En IA, c’est pareil : la transformée de Hough permet à une IA de voir des lignes droites, même si elles sont interrompues (la présence d’un meuble devant une plinthe n’amène pas à croire qu’il y a deux plinthes ; une ligne droite pointillée est perçue comme une ligne droite et pas comme une collection de segments).
La situation est compliquée par
- des effets de perspective (un angle droit n’est pas vu comme droit à cause de la perspective ; les distances ne sont pas respectées par la perspective),
- les troubles de la vision (l’astigmatisme par exemple fait voir deux droites là où en réalité il n’y en a qu’une),
- le fait que la reconnaissance des lignes est plutôt concentrée sur la vision centrale (la vision périphérique étant moins bonne chez les élèves atteints du syndrome de Down ou de certaines formes d’autisme, peut expliquer les mauvaises performances de ces élèves à des jeux de connexion),
- le fait que la présence d’une ligne transversale gêne la perception de la continuité de la ligne intersectée par cette transversale. Par exemple un adulte verra des enluminures celtes [1] comme celle-ci [2]
en relief, alors que pour un jeune enfant, il n’y a que des morceaux de courbes qui se touchent.
C’est pour aider à retrouver cette compétence de vision des lignes, de leur continuité par prolongement, de leur courbure et de leur inclinaison, qu’a été menée l’expérience relatée ici.
L’expérience devait se mener en trois phases :
Phase 1 : évaluation avant expérimentation
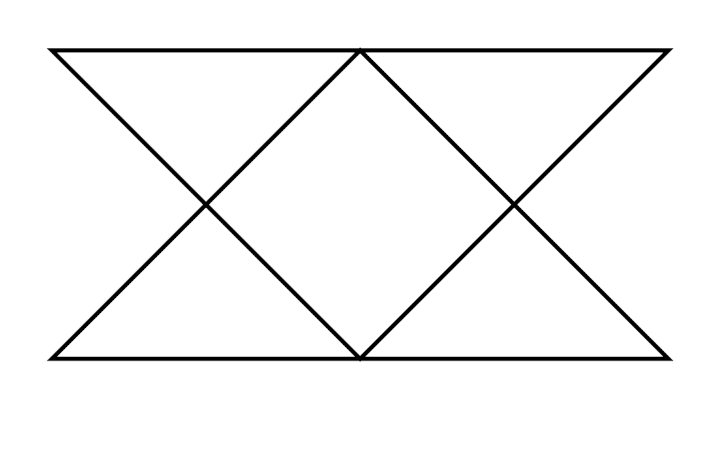
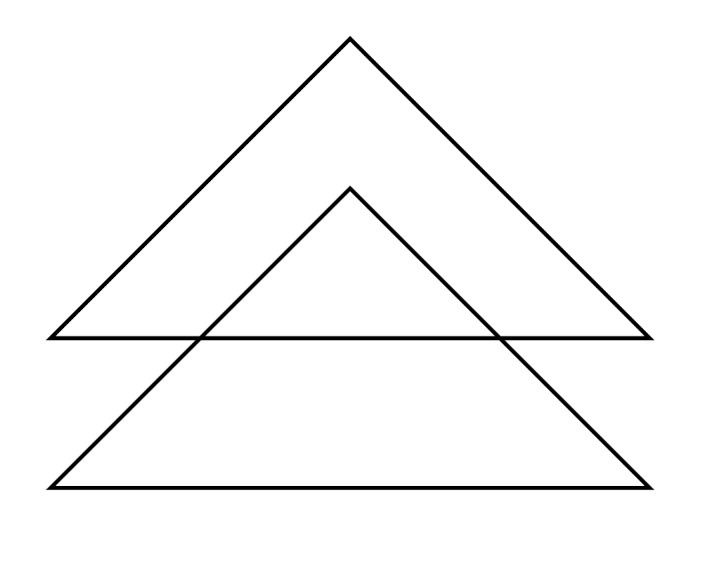
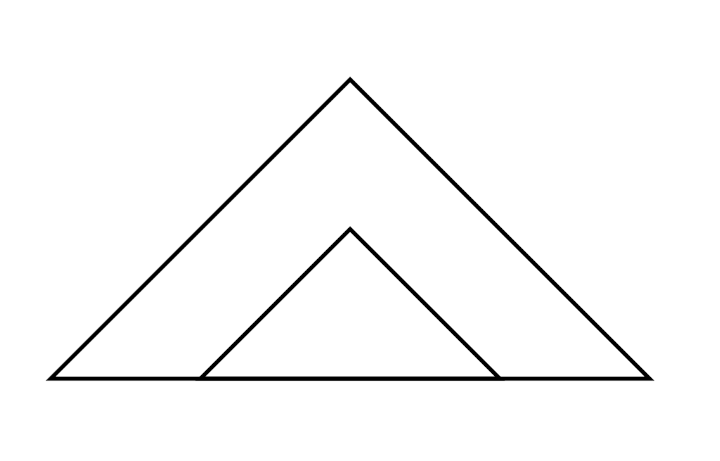
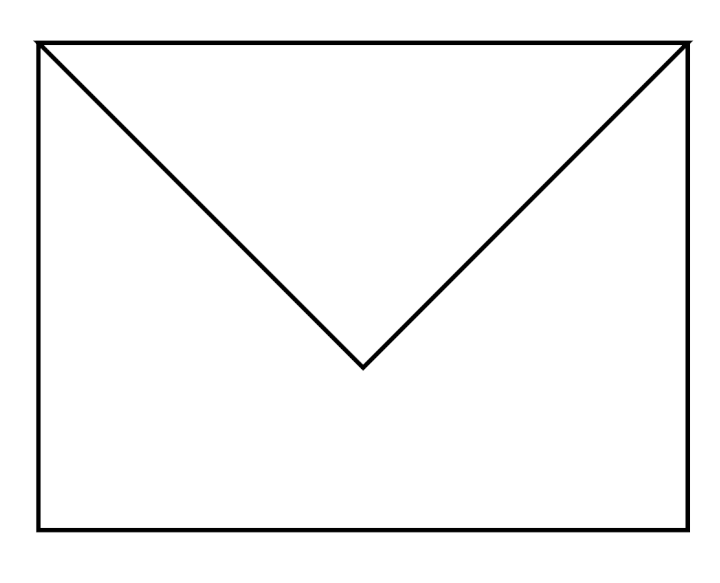
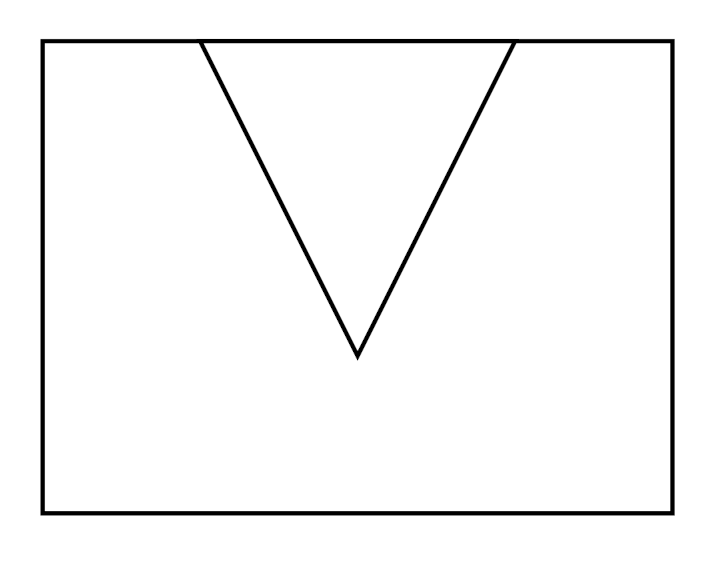
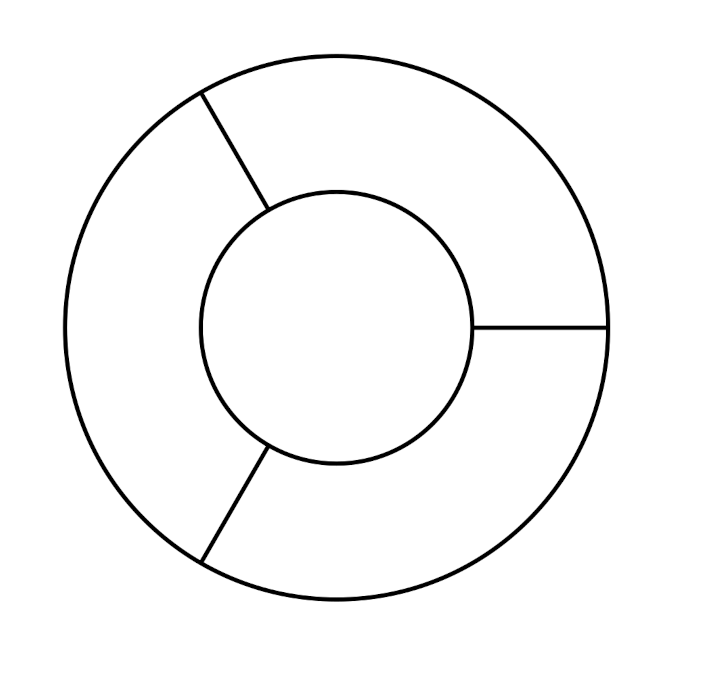
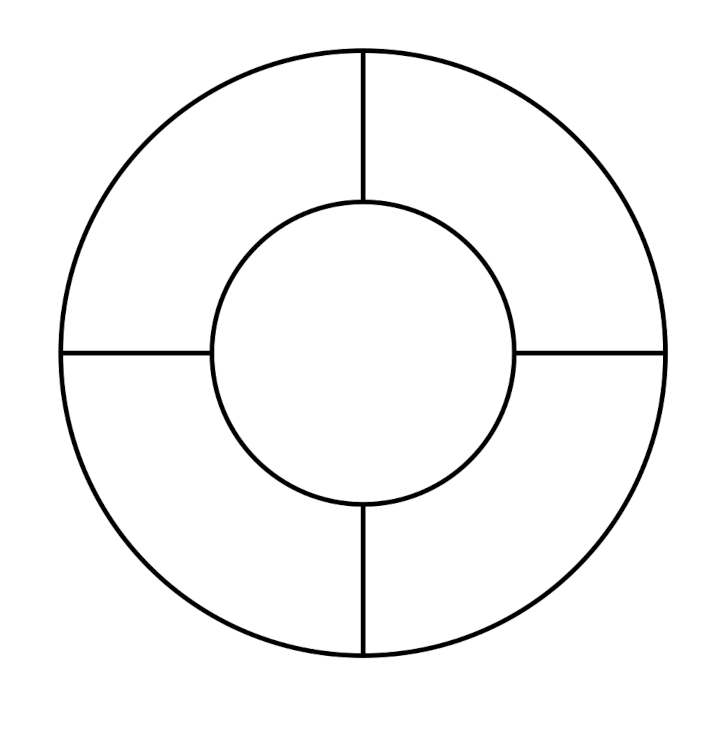
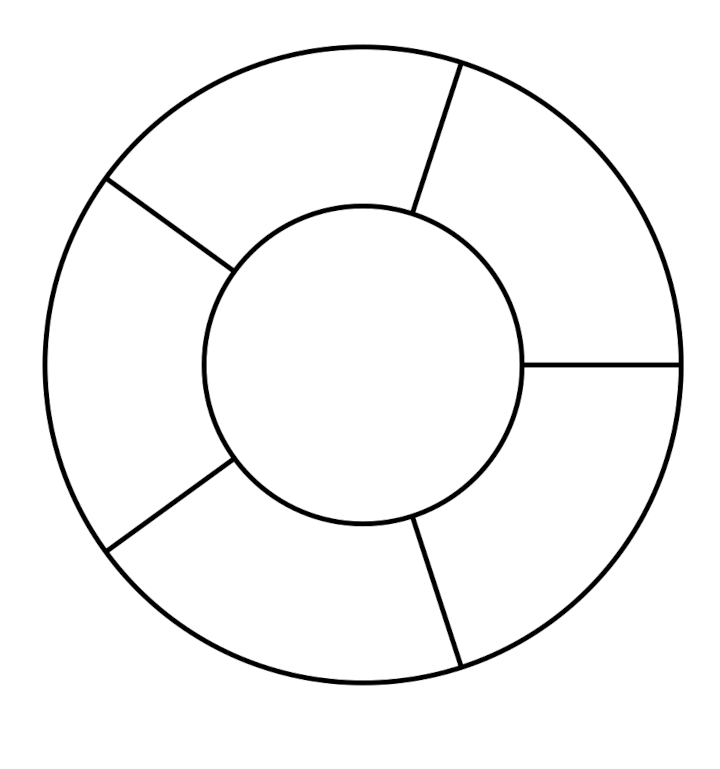
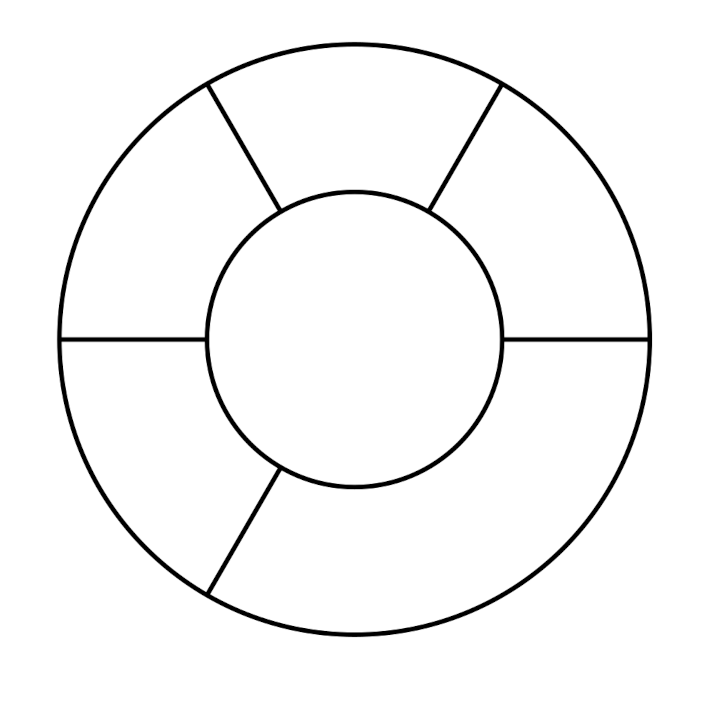
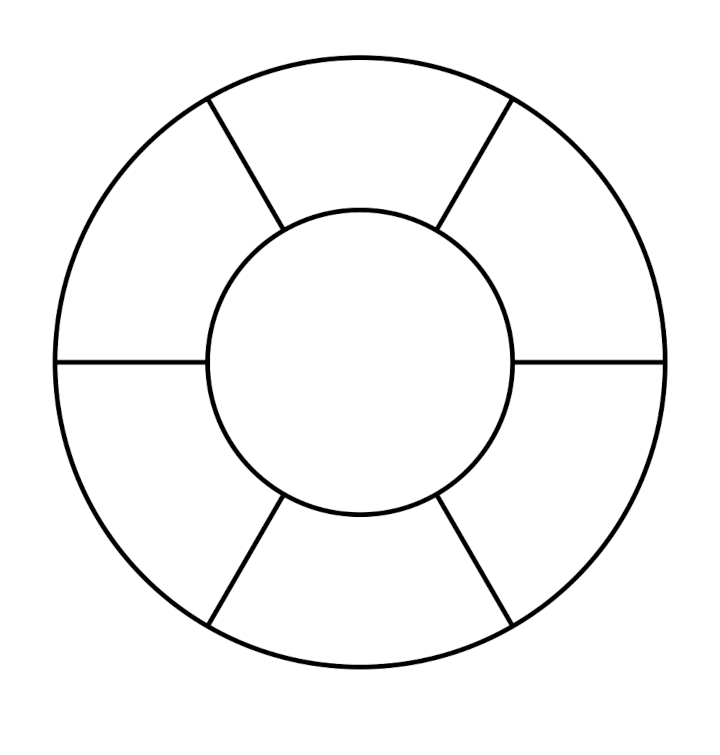
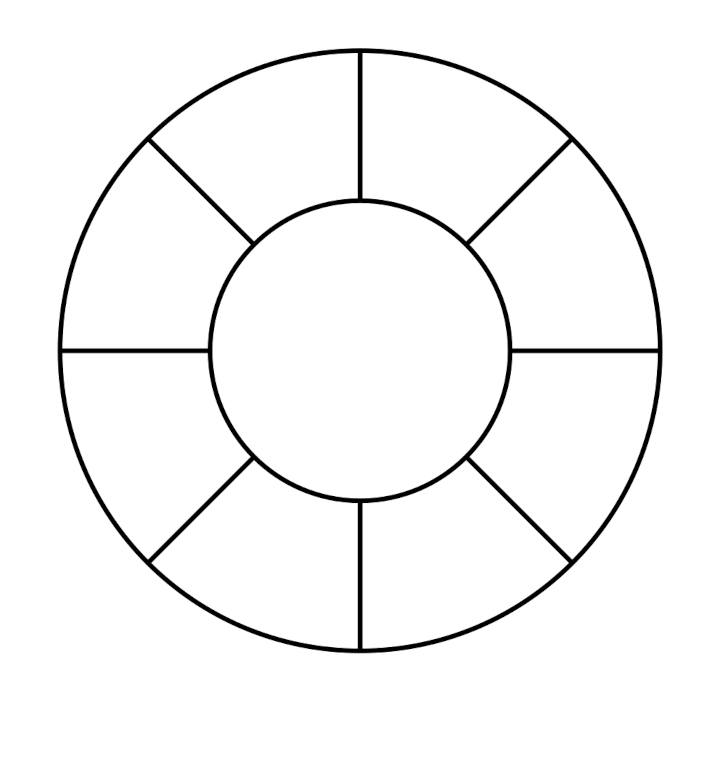
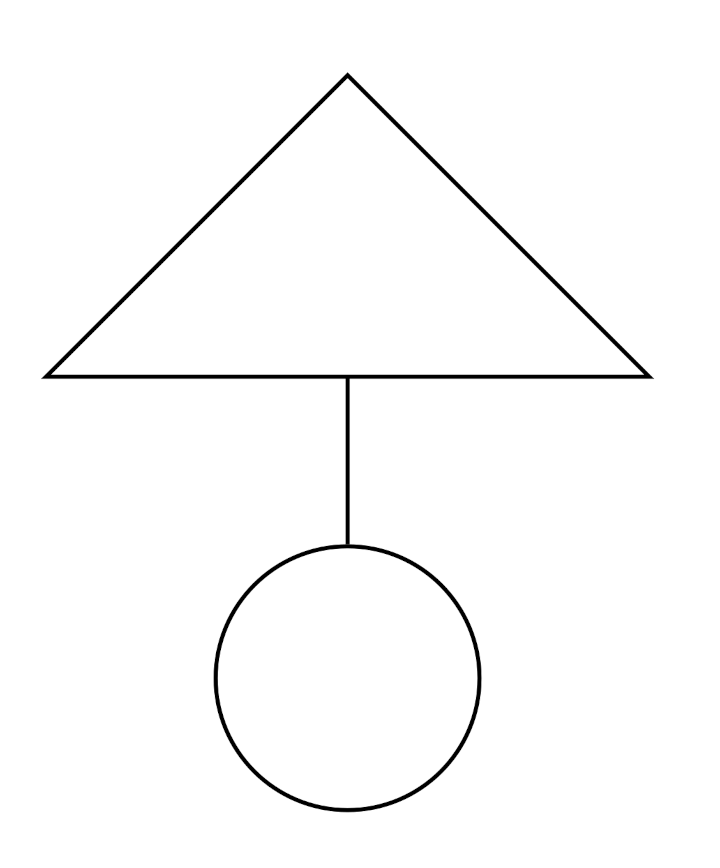
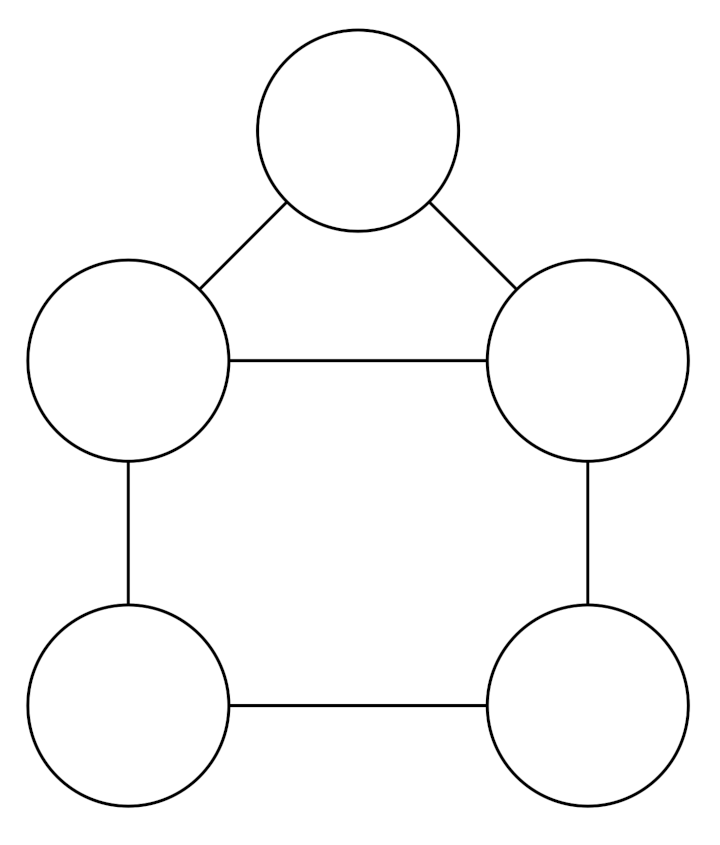
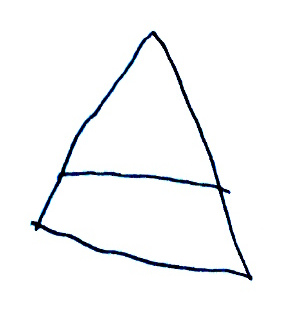
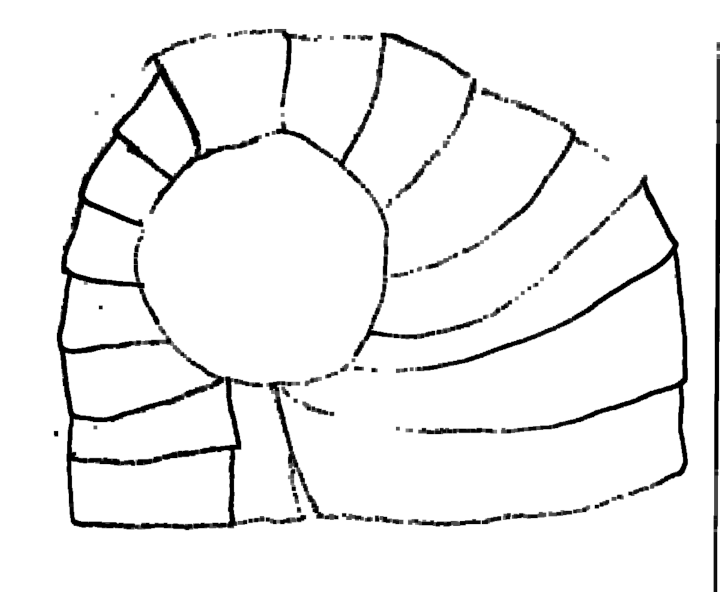
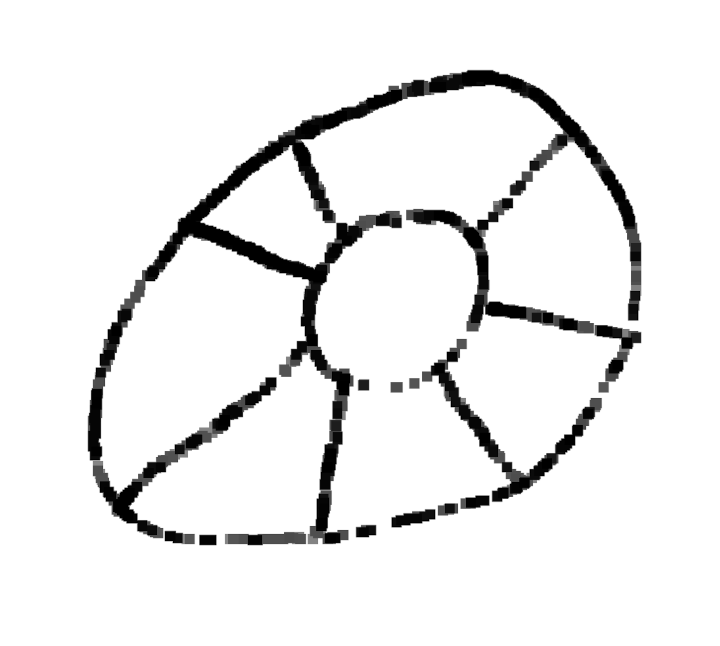
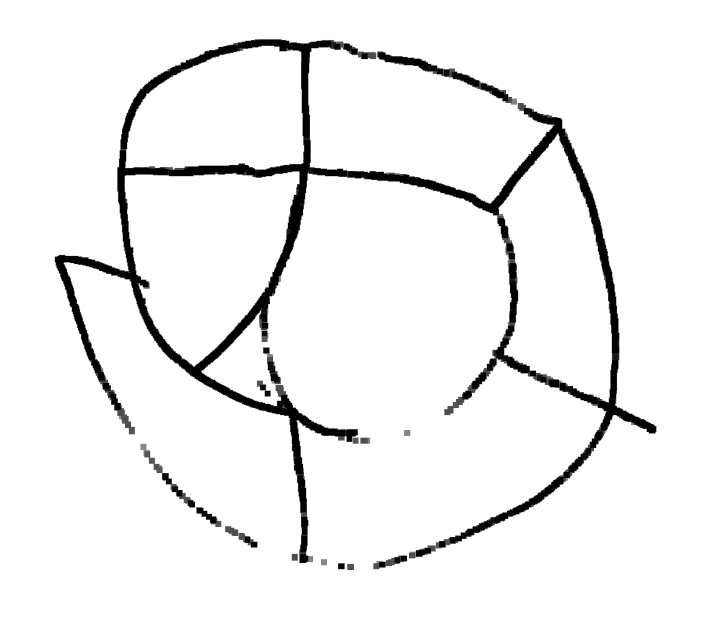
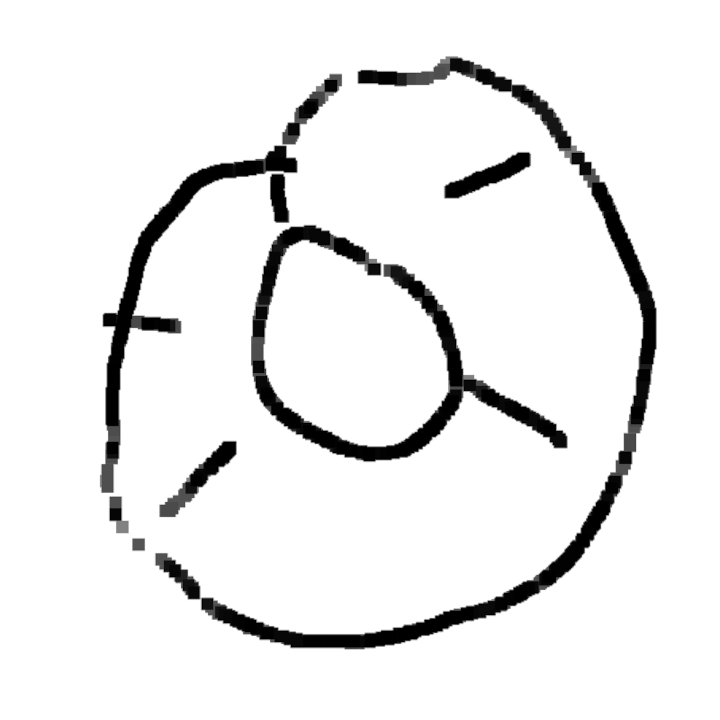
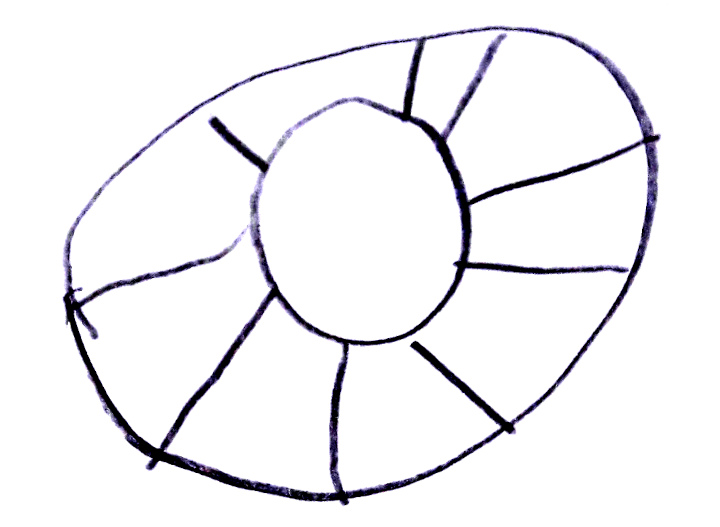
Tous les cobayes devaient tenter de recopier des dessins comme ceux de ce document :
On pouvait envisager de noter des compétences comme
- le fait que les lignes droites soient bien droites
- l’absence d’angles en reproduisant un cercle
- le fait que les traits qui sont à l’intérieur d’un cercle, ne débordent pas sur la copie de ce cercle
- le respect du nombre de traits ou d’angles
- l’alignement des morceaux d’une droite partiellement cachée
- les contacts entre courbes ou lignes brisées (par exemple la lettre b n’est pas identique, comme glyphe, au mot lo)
Les résultats devaient être archivés pour permettre une comparaison avec ceux de la phase 3. Mais aussi, s’il y avait eu suffisamment de cobayes, on aurait pu chercher la répartition statistique des résultats, afin de répartir les cobayes en groupes homogènes.
Phase 2 : le jeu
Ensuite, on devait répartir les cobayes entre un groupe témoin et un groupe de joueurs (ou plusieurs groupes, un groupe par jeu) pour permettre au jeu d’améliorer (ou pas, le but de l’expérience étant justement de déterminer un éventuel apport des jeux pour l’apprentissage) les compétences de prélecture. La phase 2 devait être la plus longue pour permettre l’apprentissage (en plusieurs séances) de la règle des jeux, et l’observation des erreurs durant les jeux.
Phase 3 : évaluation postérieure à l’expérimentation
Le même jeu de tests (figures à reproduire) devait ensuite être soumis à tous les élèves, avec la même manière de noter les compétences. Avec un volume de données suffisamment important pour limiter les biais statistiques, on aurait pu chercher alors s’il y a une corrélation entre la pratique de certains jeux (et lesquels) et la vitesse d’apprentissage de la lecture.
Pratiquement rien de tout cela n’a pu être fait :
- Des mutations, promotions, interventions dans d’autres expérimentations ont fait que l’effectif des équipes s’est réduit en peau de chagrin à une vitesse monstrueuse.
- Il n’est pas aisé de trouver un barème pour le genre d’évaluation choisi.
- Allez expliquer à un trisomique que, faisant partie du groupe témoin, il est privé de jeu, alors même que ses camarades s’amusent sous ses yeux...
- En Grande Section, plusieurs élèves ont appris à lire durant l’expérimentation, ce qui perturbe les observations sur les jeux (les élèves jouent-ils mieux parce qu’ils sont lecteurs, ou au contraire lisent-ils mieux grâce aux jeux de connexion [3] ?)
- S’est rapidement posé le problème de la non planarité avec certains jeux (voir plus bas)
Des premières expériences ont été menées dès le début de l’année scolaire :
| En Grande Section |
En IME |
En ULIS |
|
|
|
| La forêt enchantée, Black Path, Meander, Turnabout |
Turnabout, et Hex |
Turnabout, Truchet et Hex |
Elles ont révélé un problème avec les ponts dessinés sur les pièces de jeu : dans ces pièces (surtout si elles sont monochromes)
plusieurs élèves voient, au lieu d’un pont où une route rouge passe par-dessus une route blanche,
- ou bien un carrefour où on peut tourner à angle droit pour changer de route (ce qui revient à sauter du pont, ce qui est bien entendu interdit par la règle du jeu),
- ou bien deux routes blanches, interrompues par la route rouge.
Le même problème se pose parfois aussi lorsqu’on construit une route en alignant deux pièces de jeu, la jonction entre ces pièces de jeu suggérant une interruption du flot. Pour cela, jouer au train électrique serait sans doute plus fructueux, en raison du caractère à la fois kinesthésique et tridimensionnel de ce jeu.
Ce problème de pont a amené à privilégier des jeux où n’apparaissent pas ce genre de croisements, soit jouer uniquement avec des pièces de ce genre (mais en version monochrome) :
soit jouer avec des hexagones comme dans les jeux Hex et Y.
Routes sans croisement
Avec les pièces de Turnabout sans croisements (appelées pavés de Truchet), le plus vieux jeu à deux joueurs connu est un jeu de Lewthwaite appelé meander et qui est une sorte de taquin (les pièces en papier volent trop facilement et frottent chaotiquement les unes contre les autres).
Plus récemment, Cameron Browne a créé les jeux
Mais les travaux de Browne sur les pavages de Truchet permettent d’utiliser ces pavés pour laisser libre cours à sa créativité. Voir aussi cet article sur image de maths pour une approche notamment historique.
Le jeu bridg-it créé par David Gale dans les années 1940, se joue avec des bâtons de deux couleurs à poser sur des piliers de ponts. La règle du jeu interdit que deux bâtons se croisent, ce qui évite là aussi le problème des ponts. Le jeu bridg-it a déjà été testé à l’école de Saint-Mandé mais pas à l’école maternelle. Le matériel de jeu consistait en ardoises sur lesquelles les sommets étaient peints, ce qui permettait de rejouer ad libitum simplement en effaçant les ponts. Noter que la version ludii se joue avec des pions dont certains sont collés au plateau avant le jeu. Avec des pions en forme de dalles carrées, on se rapproche de la catégorie Hex décrite plus bas.
On peut penser aussi au jeu Sprouts qui peut se jouer sur une ardoise commune aux deux joueurs : dans ce jeu le graphe est planaire donc il n’y a pas de croisements ni de ponts. Le jeu de Sprouts a déjà été testé à l’école des 400 (en cycle 3), à l’école Aristide Briand (du CE1 au CM2), à l’école Jean-Albany du Grand Tampon (en cycles 2 et 3), mais aussi par quelques élèves de Grande Section.
Pavés à couleur unie
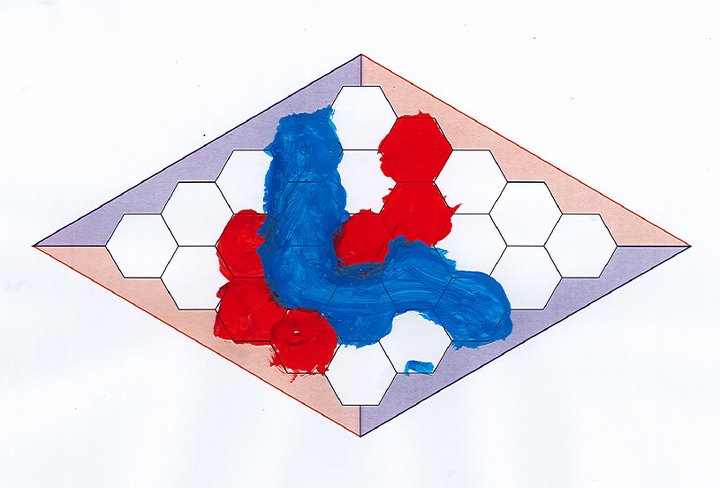
Le problème de la perception des ponts est également illustré par cette situation (Hex en CP) :
On y voit ce que David Gale appelait le
théorème de Hex : Il n’est pas possible qu’un chemin rouge et un chemin bleu se croisent sans que l’un interrompe l’autre.
En effet, pour cela il faudrait que la dalle où se croisent ces chemins soit à la fois rouge et bleue, ce qui est interdit par la règle du jeu.
Le jeu Hex a déjà été hexpérimenté dès la Moyenne Section. La suite de l’expérimentation a donc porté sur le jeu Y (dont l’ancien nom est triangle). Voici une partie de Y jouée en Grande Section :
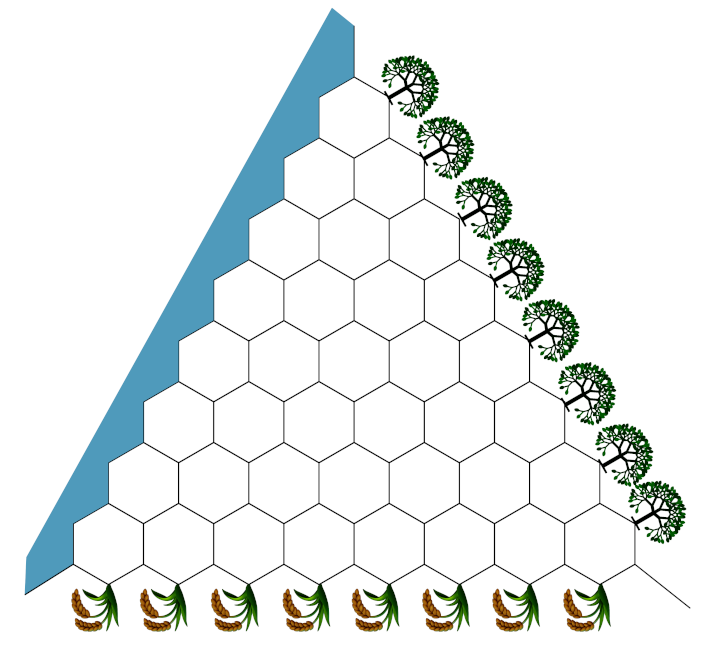
Le plateau de Y sur lequel les élèves ont joué est ici :
La situation est la suivante : les bleus et les rouges veulent faire cuire du riz. Pour cela il faut pouvoir accéder
- à la rizière (en bas ; pour avoir du riz à faire cuire)
- à la forêt (à droite ; pour avoir du bois comme combustible)
- à la rivière (à gauche ; pour l’eau de cuisson)
Chacun est donc chargé de construire un chemin de sa couleur pour accéder aux trois ressources. Ce qui, compte tenu des situations géographiques, revient à relier les trois côtés du triangle.
Dans les jeux Hex et Y, des grands hexagones posés par terre permettent aux élèves de tester la continuité du chemin en marchant dessus sans sauter par dessus une dalle.
L’évaluation vue comme un jeu
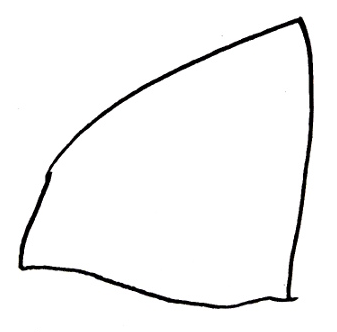
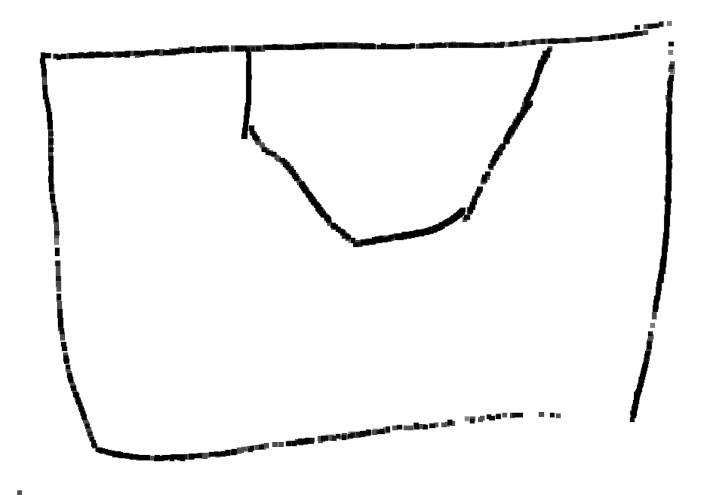
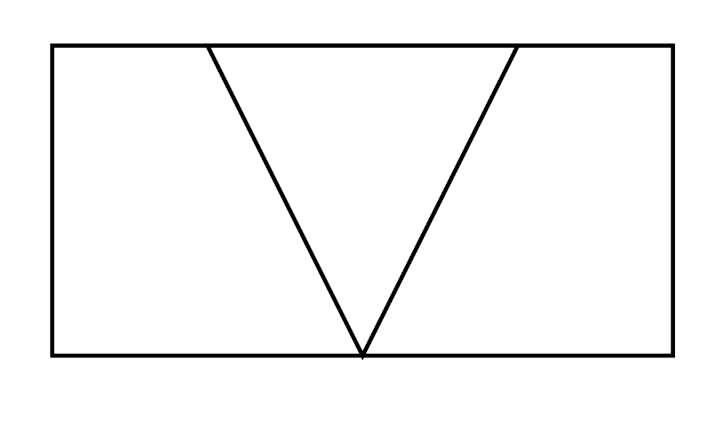
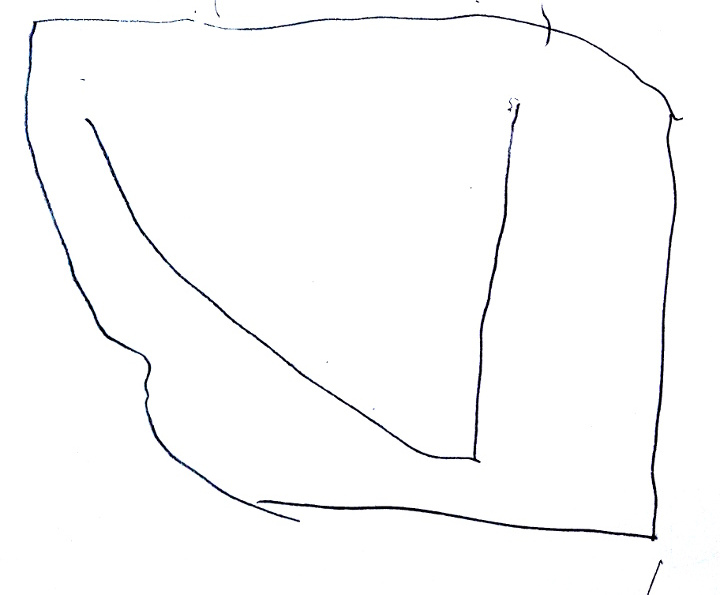
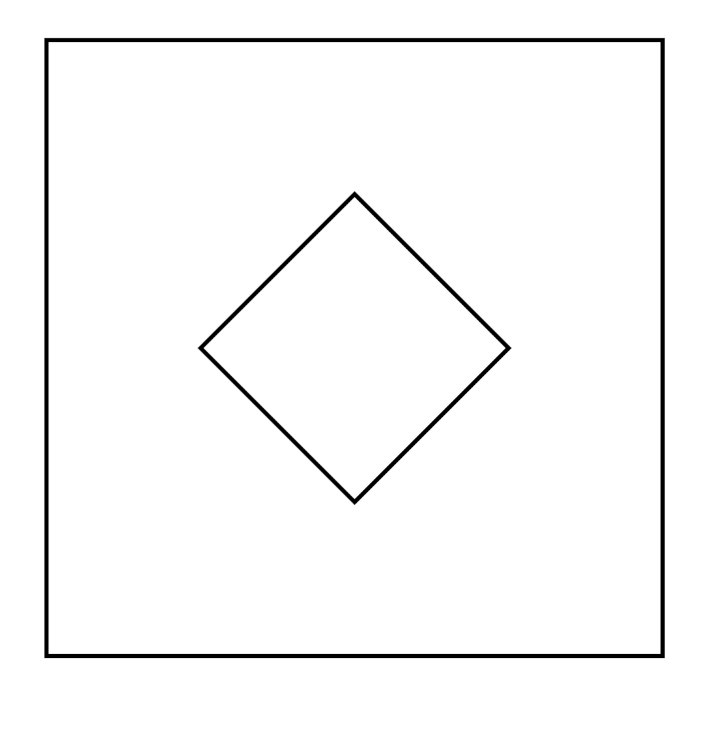
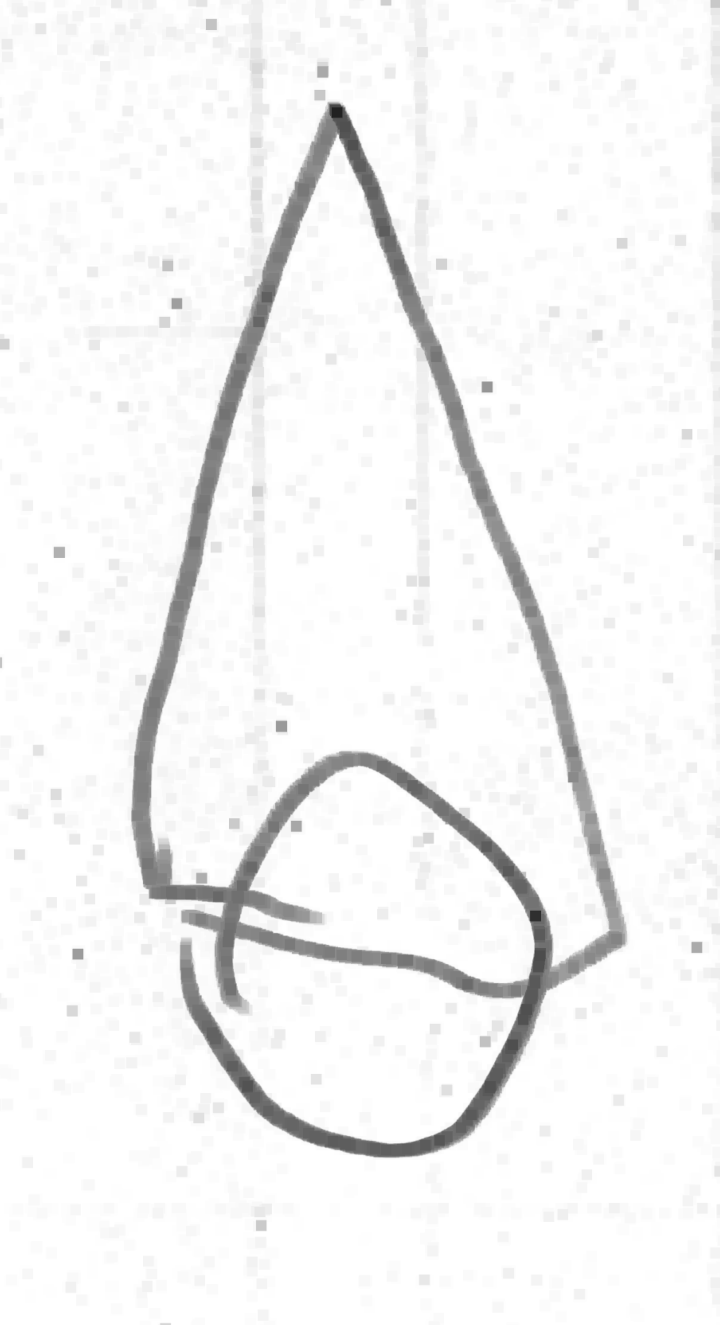
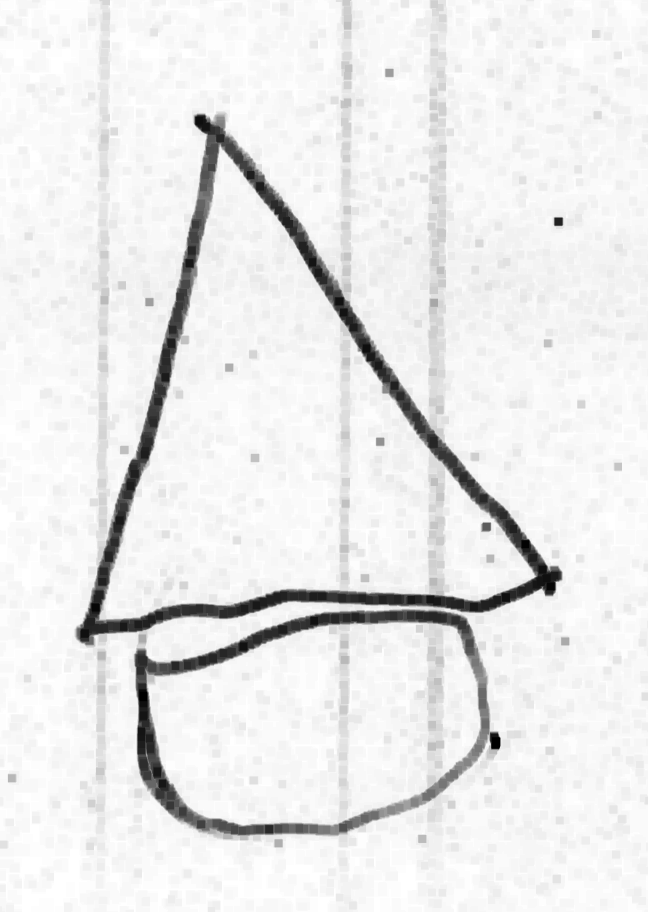
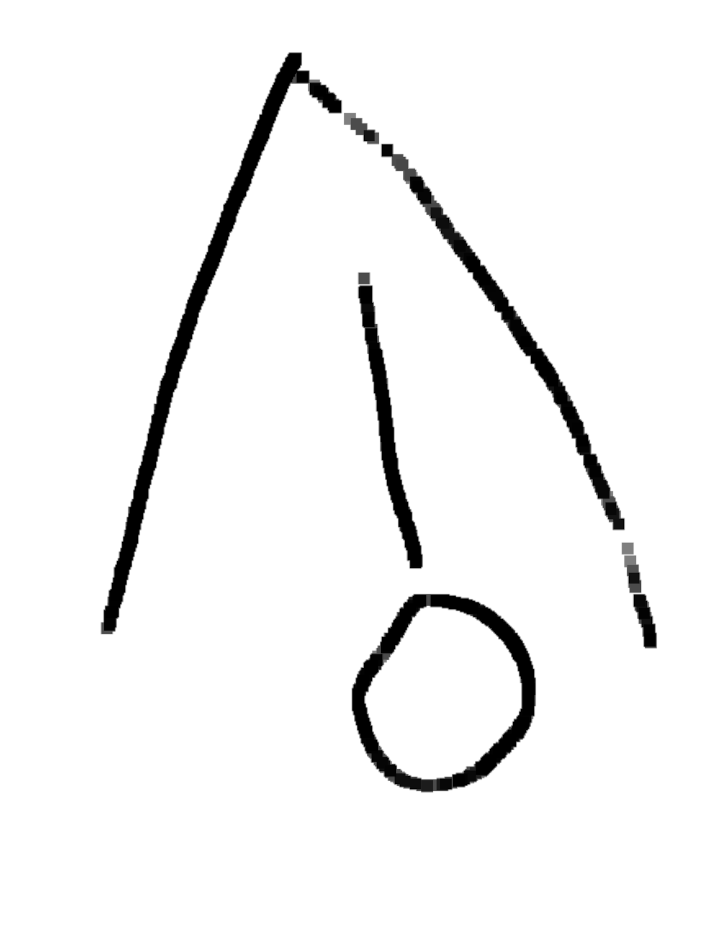
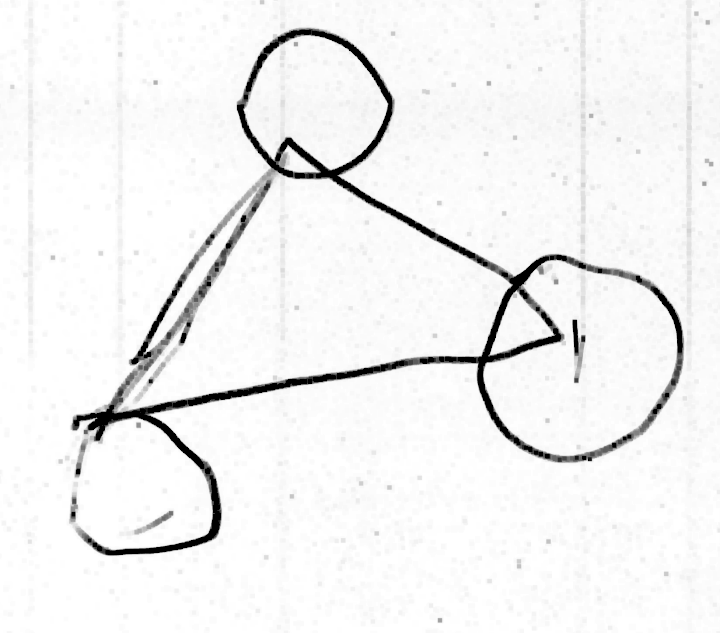
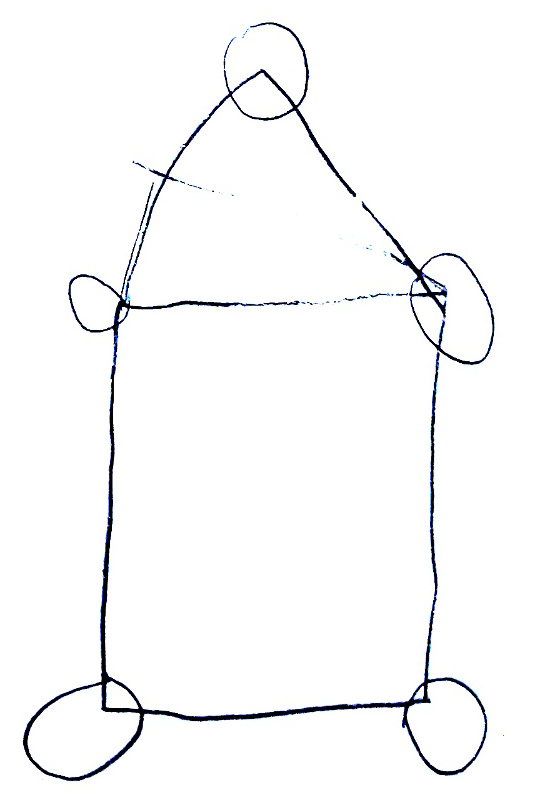
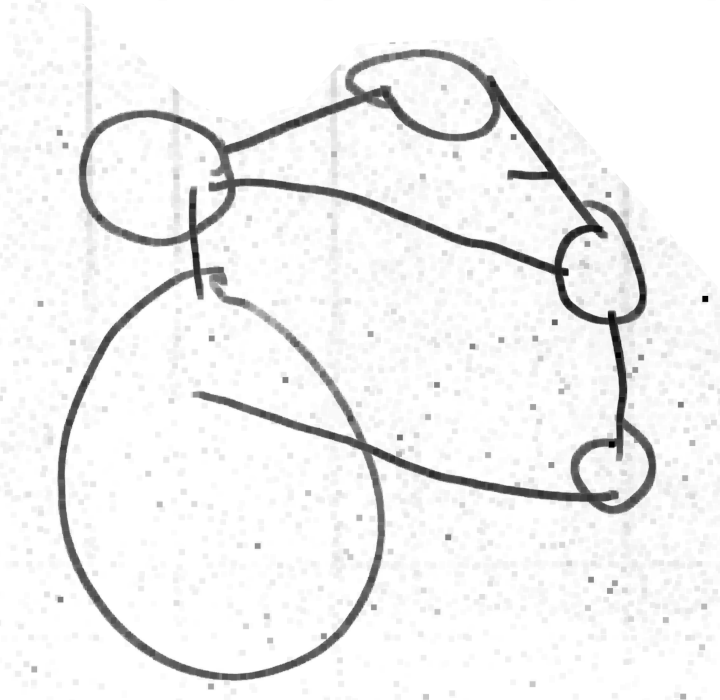
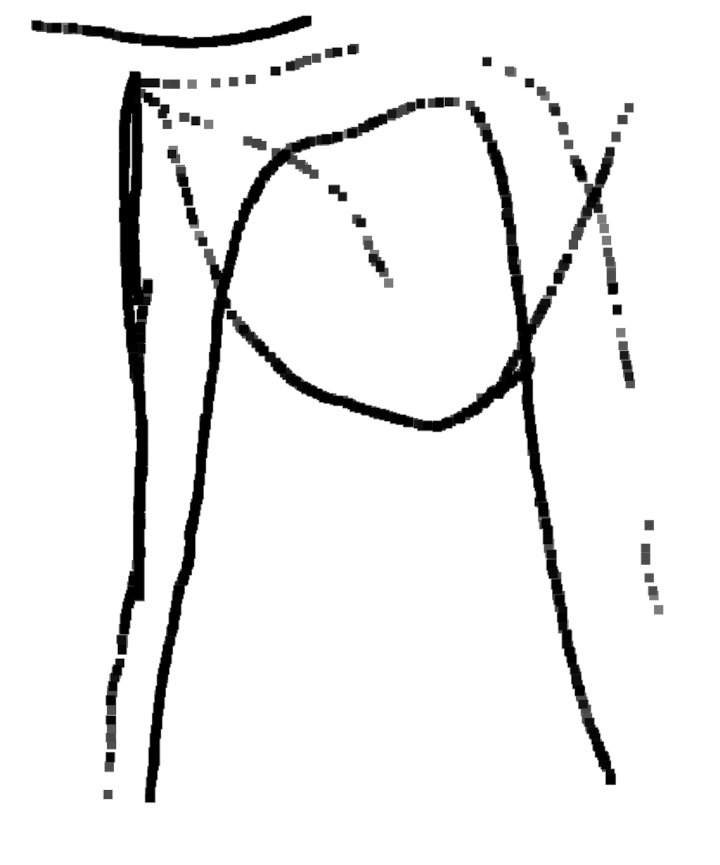
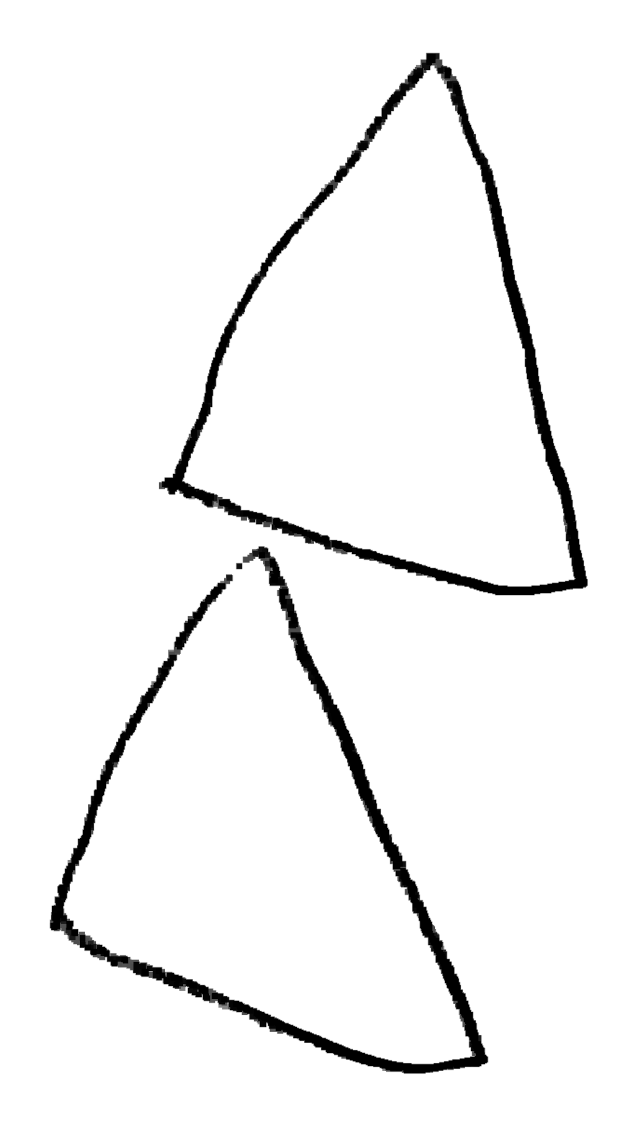
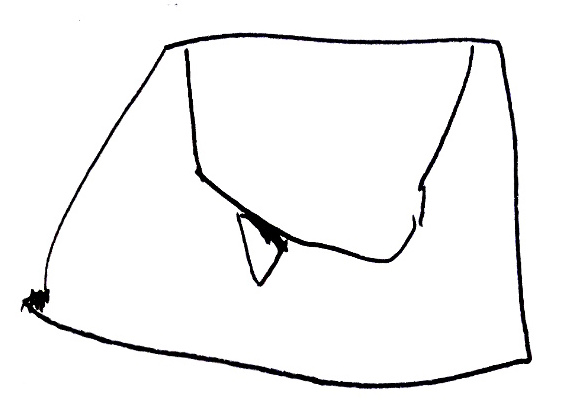
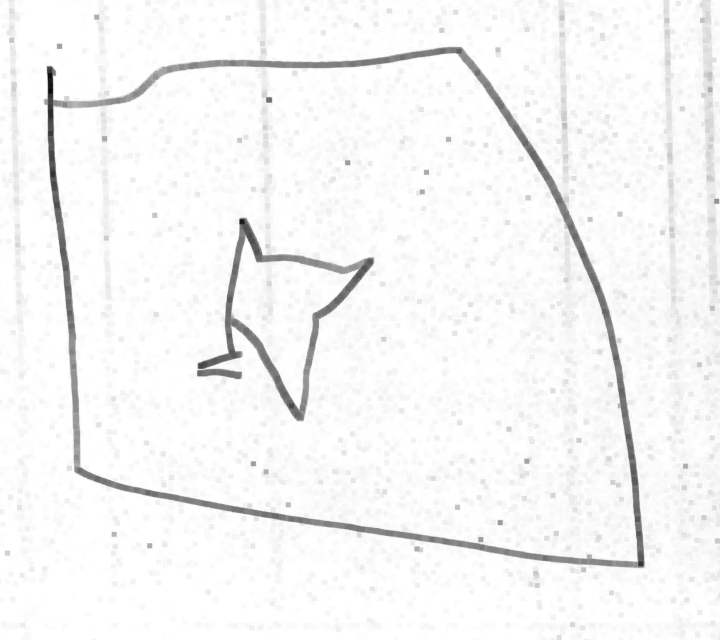
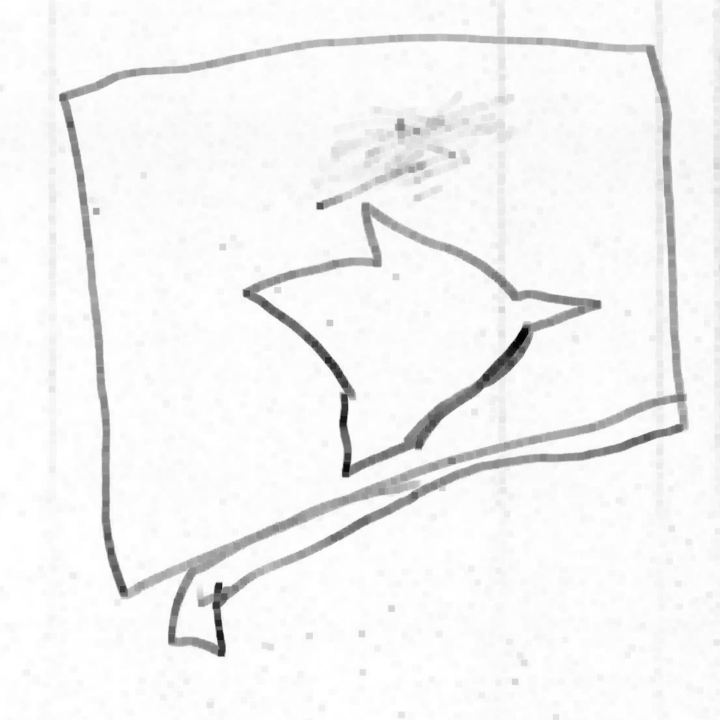
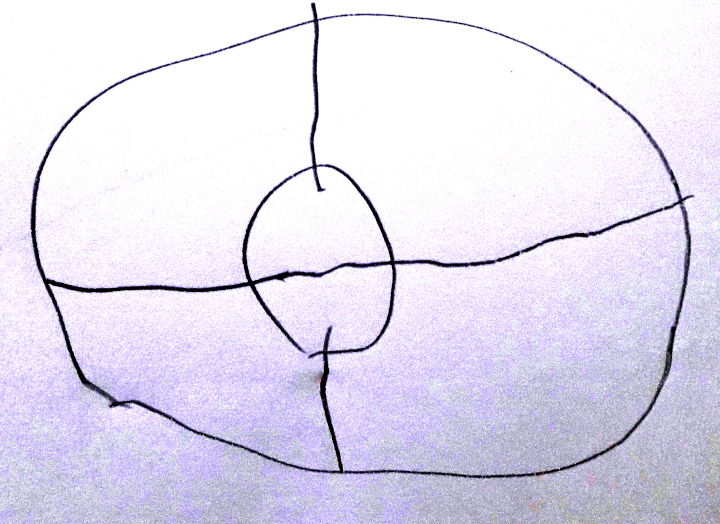
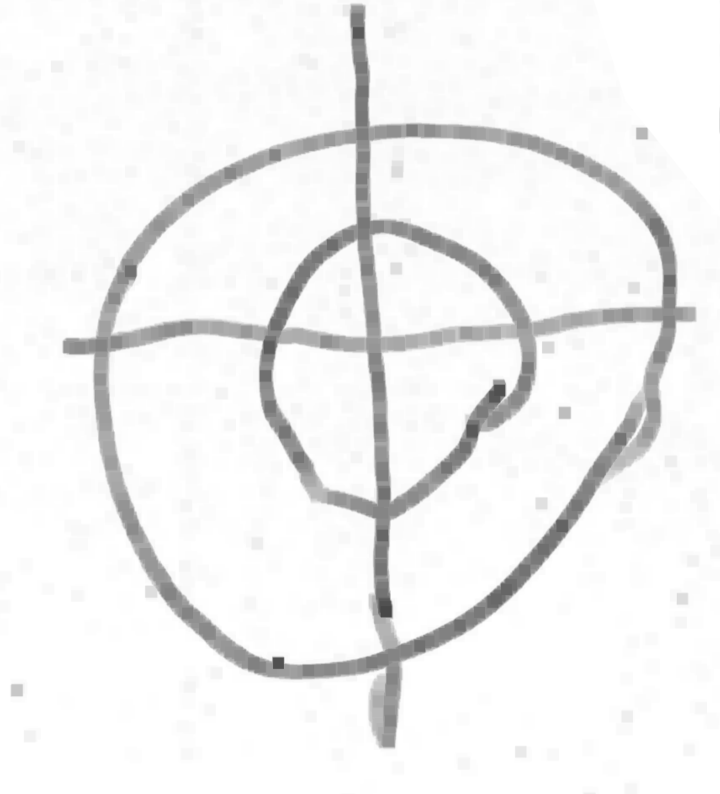
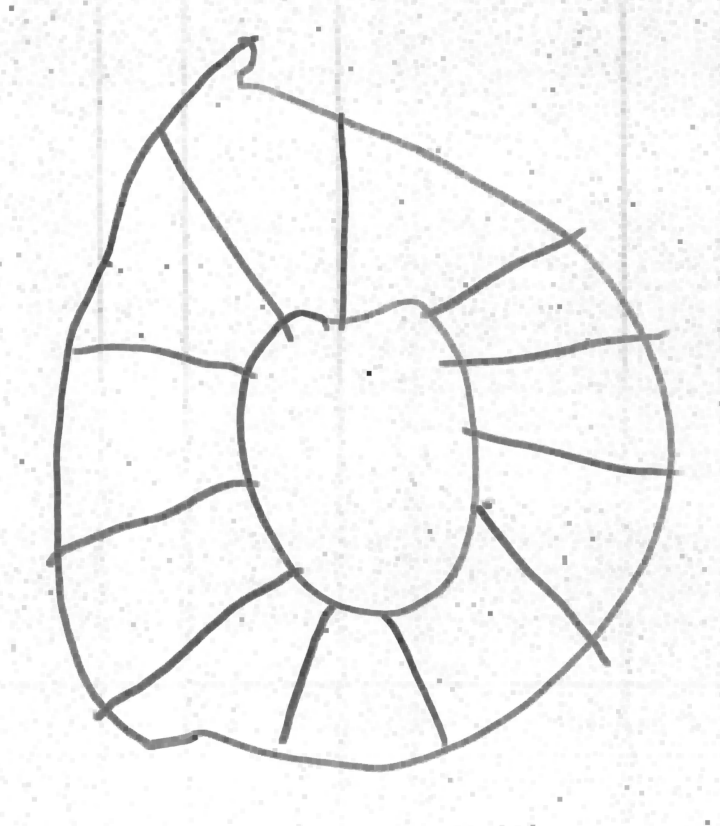
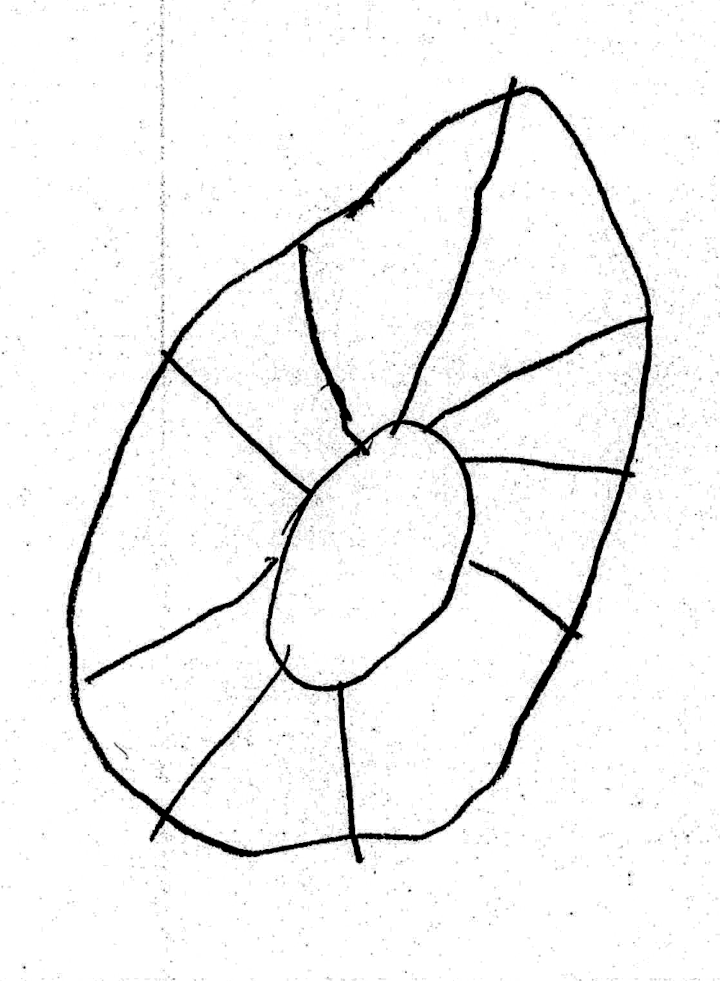
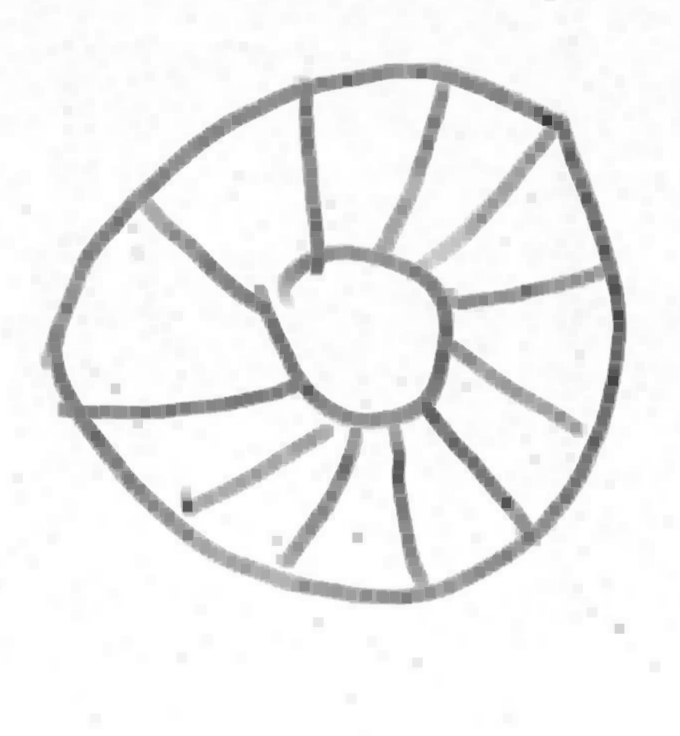
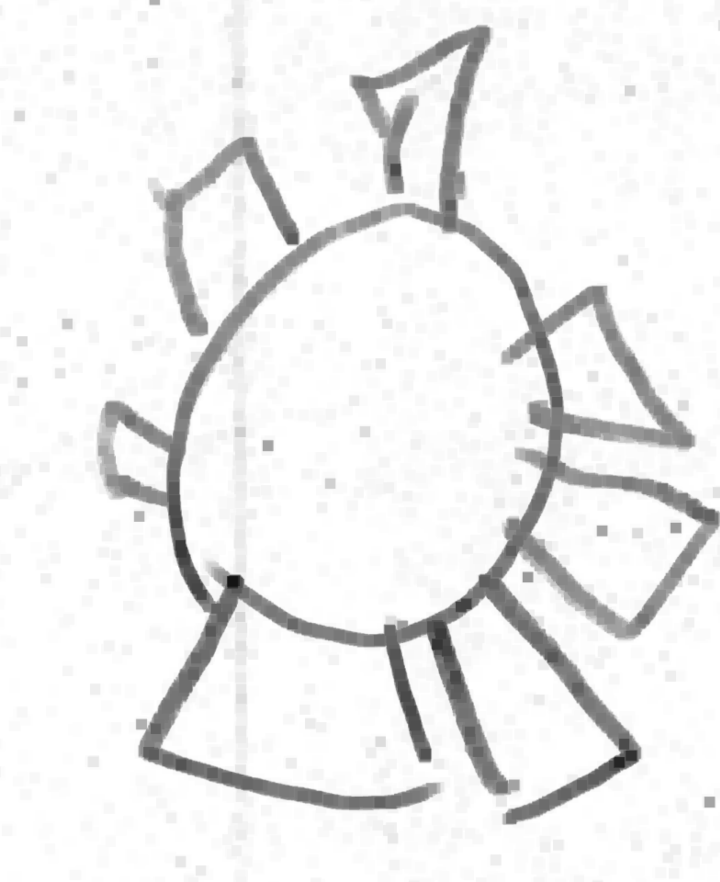
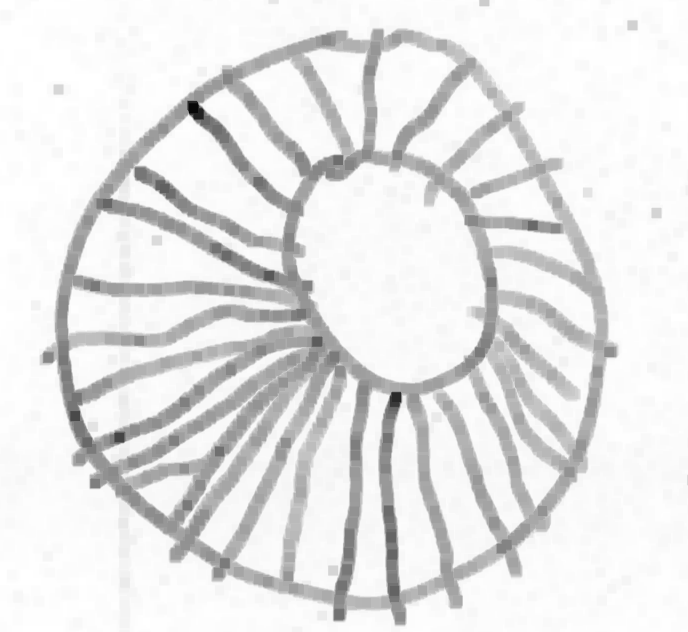
Même si les évaluations de la phase 1 n’ont pas été utiles, elles montrent des choses intéressantes, notamment pour la construction du nombre. Ci-dessous on montre l’original et différentes copies, montrant certaines difficultés que connaissent les élèves. Recopier une figure géométrique à la main, est un exercice court que les élèves adorent.
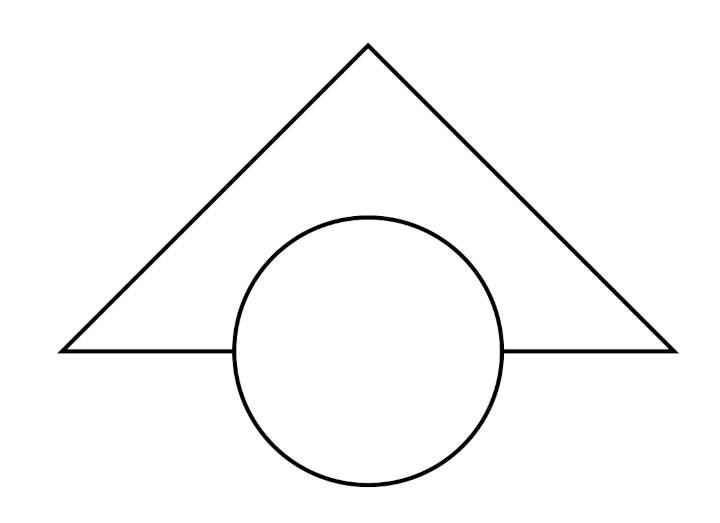
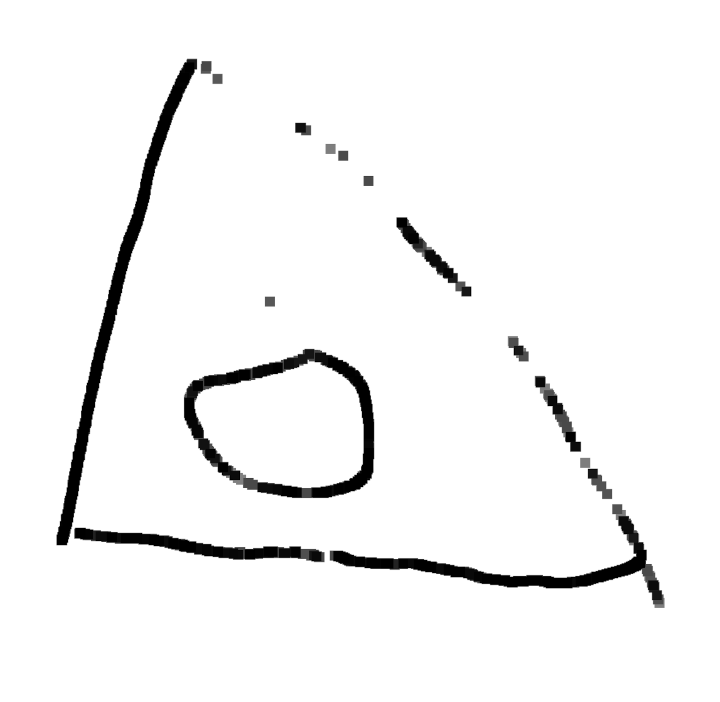
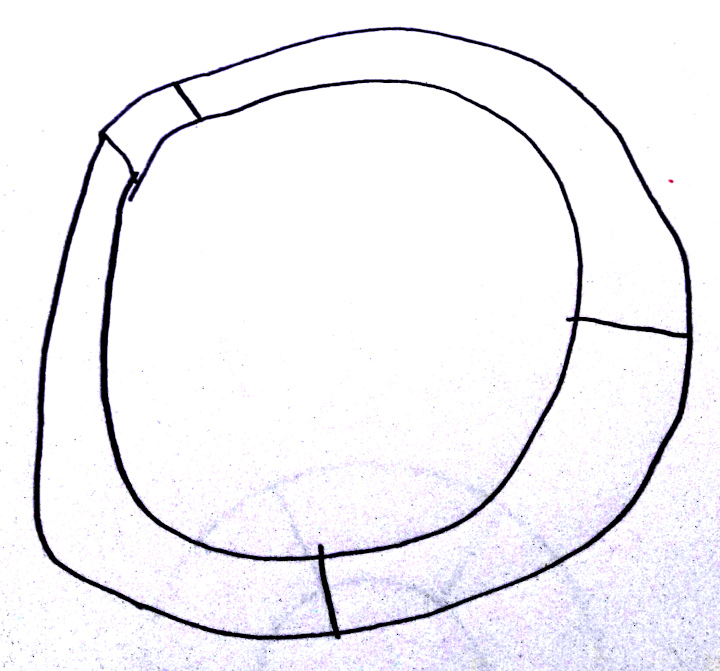
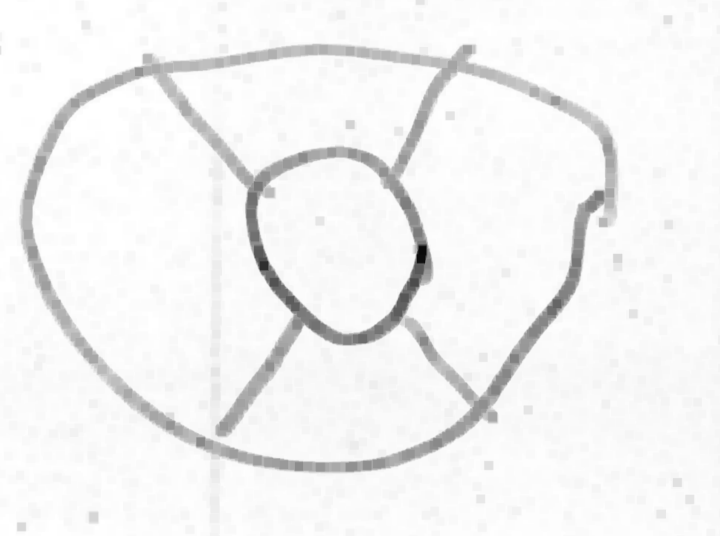
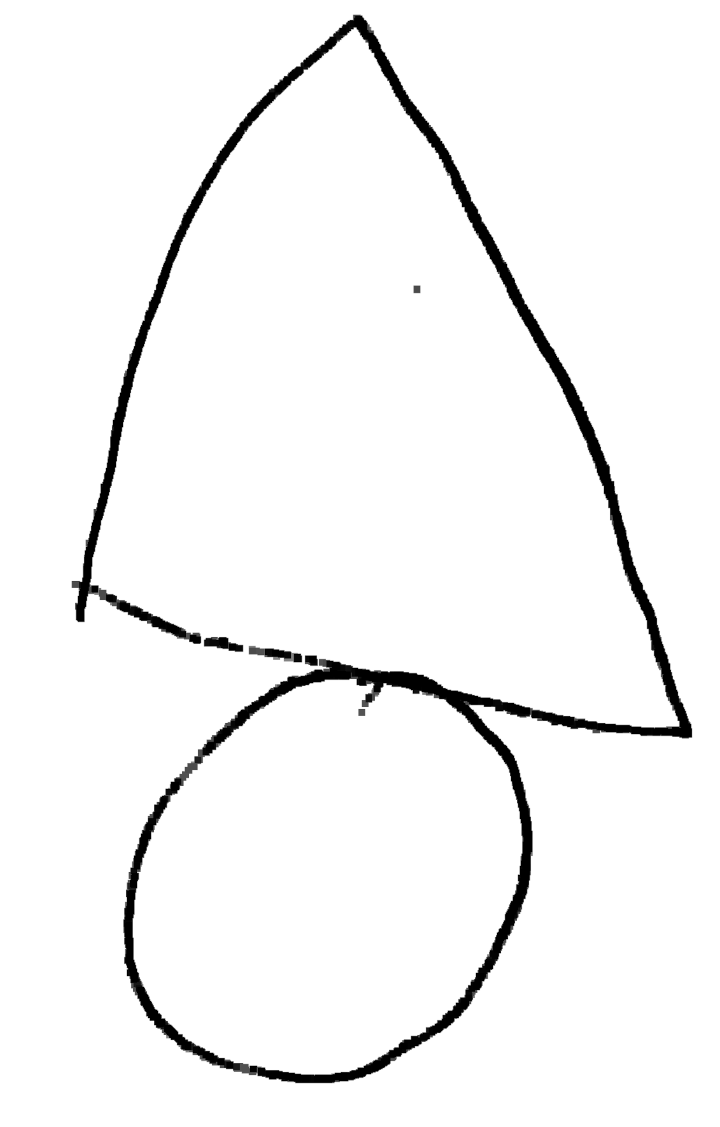
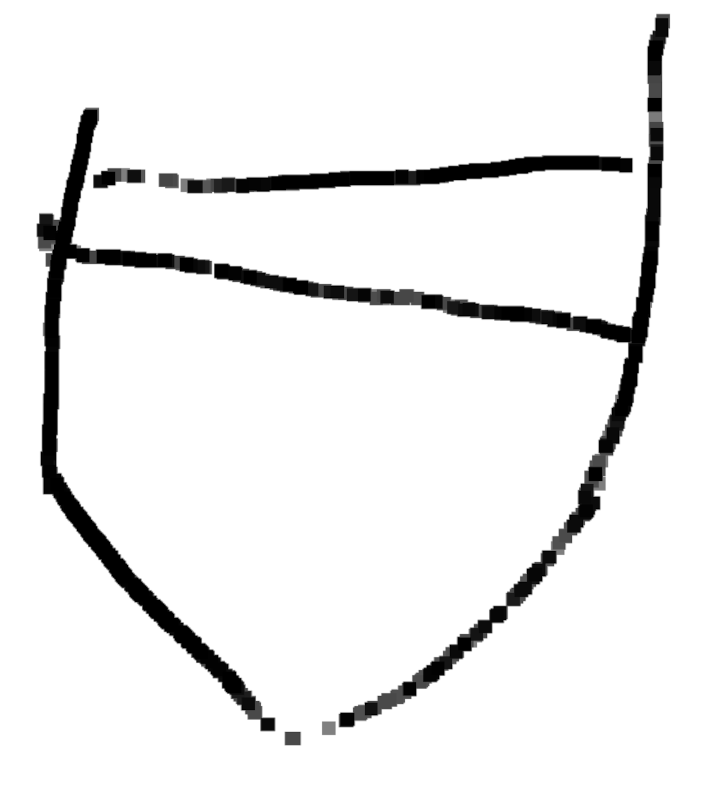
Grande section, n’a pas vu le disque cacher le segment.
Ulis, n’a pas vu le disque cacher le segment : peut-être peu sensible au problème du pont !
IME, fait avec soin donc probablement fidèle à la vision (ceci dit, le passage par la verbalisation peut créer une distorsion)
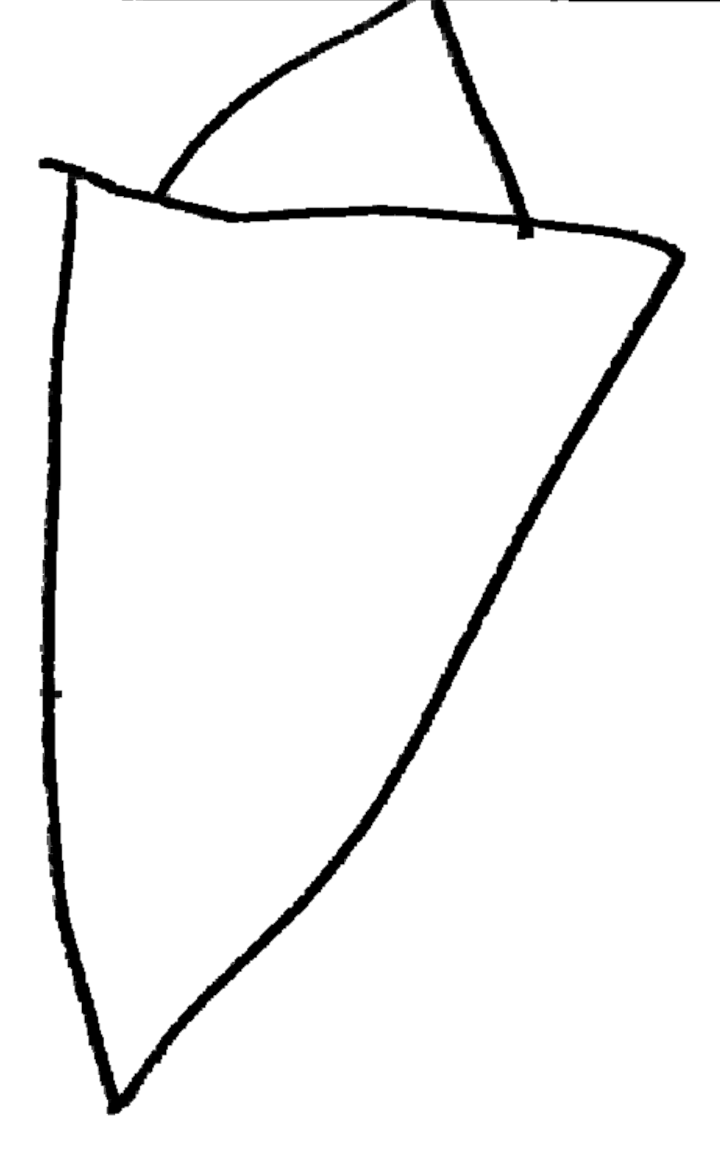
IME, similaire à l’onglet précédent.
IME
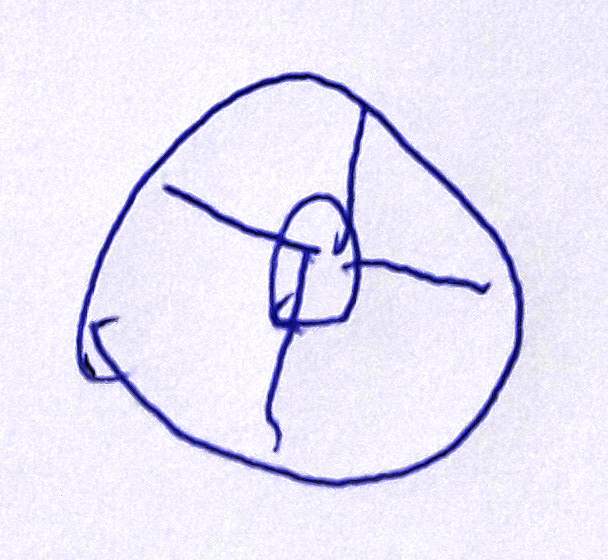
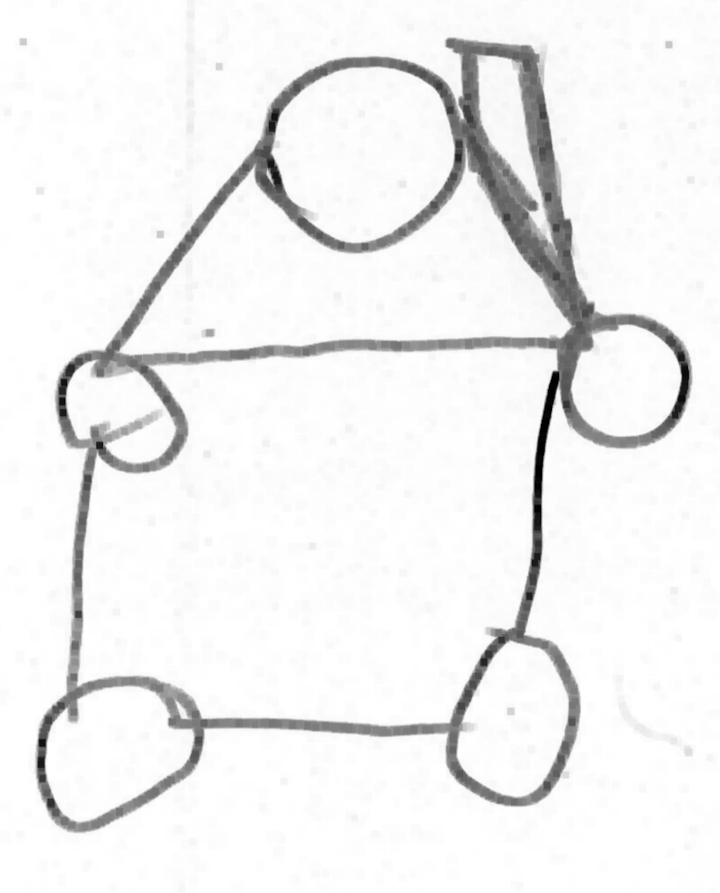
Grande section ; a vu non pas 2 triangles tête-bêche mais 4 triangles tangents.
IME
Grande Section
Ulis : les rayons débordent ; difficile de savoir si le problème est psychomoteur ou lié à la vision.
Grande section. La différence entre 3 et 4 n’est pas perçue.
Grande section ; les traits débordent.
Grande section ; les traits débordent.
Grande section ; erreur sur le nombre.
Grande section ; erreur sur le nombre (ou recherche de symétrie ?).
Grande section
IME ; erreur sur le nombre




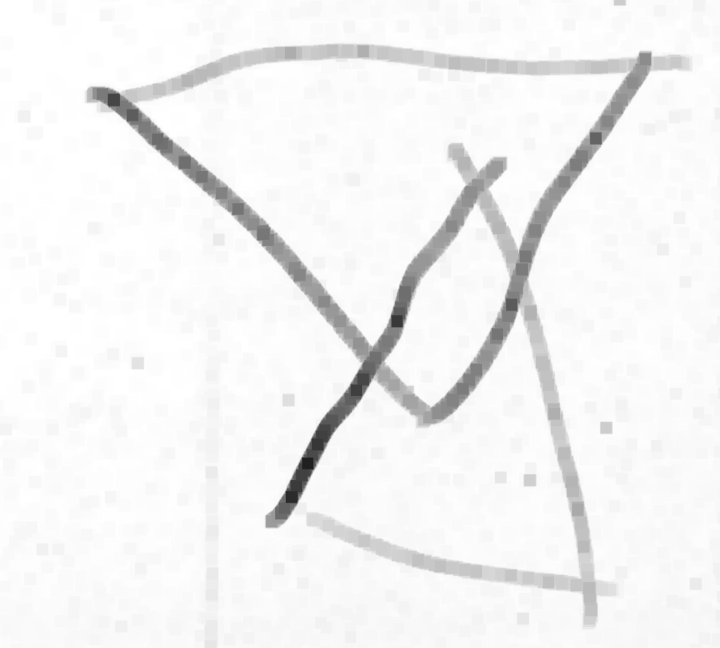
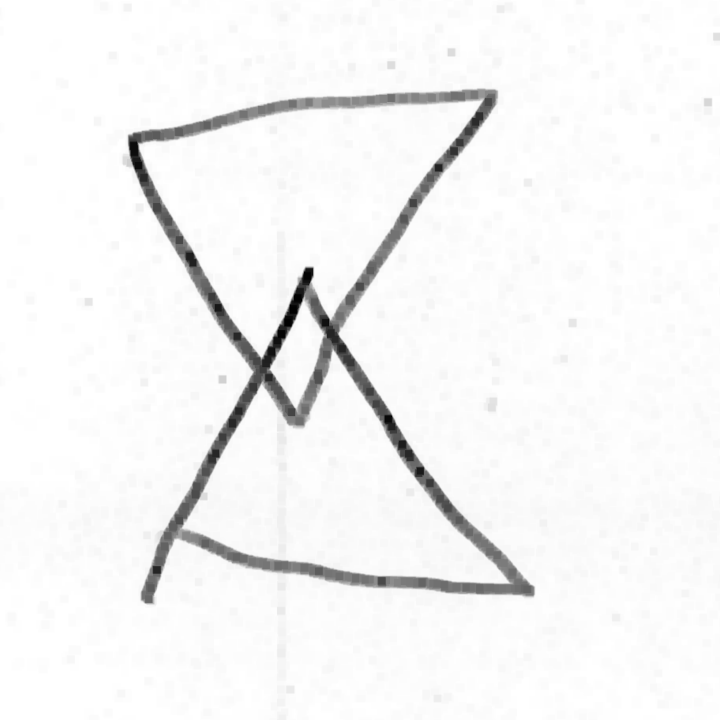











Commentaires