Le robot peut très bien être une tortue Python ! Dans ce cas il vaut mieux qu’au lieu d’avancer de $\frac{1}{n(n+1)}$ à chaque étape, elle avance de $\frac{100}{n(n+1)}$ et qu’elle essaye de sortir du cercle de rayon 100.

On peut commencer en interactif :

puis construire un segment à 100 pixels de l’origine (pour voir où la tortue doit aller) puis écrire une boucle :

Cette méthode permet de cacher les additions dans le caractère cumulatif de la mémoire de la tortue. On obtient ceci après 20 itérations :

Pour faire un peu plus "algorithmique" avec une variable incrémentée (de moins en moins) on peut utiliser un CaRScript comme celui ci-dessous :

Le script peut ensuite être modifié pour représenter graphiquement la suite (onglet "limite" ci-dessus) et avec une droite horizontale mobile pour conjecturer la valeur de la limite.

On peut aussi (risqué !) transformer l’algorithme en une boucle telle que

s=0;
n=1;
while(s<1){
	s+=1/n/(n+1);
	n++;
	Move("R",s,0);
}

et la question devient : "Est-ce que la boucle s’arrêtera un jour, ou est-elle sans fin ?"

SciLab

Avec SciLab, les suites (finies) sont des objets que le logiciel peut manipuler, sans boucles ni indices (sauf si on veut, la syntaxe des boucles est plutôt simple). Ci-dessous on crée la suite des n par a=1:20, puis celle des n+1 par b=a+1, puis leur produit terme à terme dans c et la suite des $\frac{1}{n(n+1)}$ dans d, à chaque fois suivis par des points-virgules pour ne pas encombrer l’écran par leur affichage. Ensuite cumsum donne la suite $u_n$ :

On a le même genre de résultat qu’un tableur, avec le même genre de manip (sans boucle ni affectation de variables numériques). Pour le graphique en rouge ("r"), en pointillés (" :") et avec des points ronds ("o"), on fait

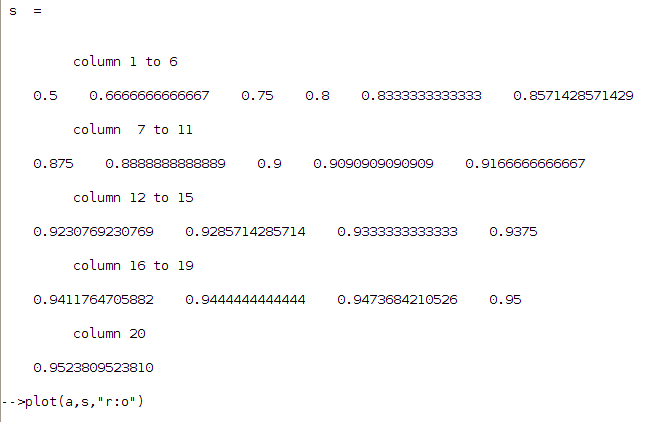
ce qui donne ceci :

Calcul formel

Le même genre de manip sous Xcas donne la valeur exacte de $u_{20}$ qui aide à faire une conjecture, renforcée par le calcul de $u_{100 000}$, puis de $u_N$ :

Quant à WxMaxima, il est écrit en LISP qui est un langage spécialisé dans les listes, alors on peut avoir les 20 premiers termes de $\frac{1}{n(n+1)}$ et de $u_n$ d’un coup :

El le paquet solve_rec permet de calculer la valeur exacte de $u_n$ en considérant celle-ci comme récurrente (en effet $u_{n+1}=u_n+\frac{1}{(n+1)(n+2)}$) :

Bref, il y a bien des manières d’étudier expérimentalement cette suite :

1. le calcul formel donne des résultats immédiatement, de façon assez interactive surtout avec le tableur d’Xcas, non traité ici ;
2. le tableur justement, non traité ici, somme assez facilement les termes d’une suite mais avec un « dollar » au début, par exemple B1=SOMME(A$1;A1) à copier vers le bas si la colonne A contient les fractions à additionner ;
3. SciLab fait des affectations sur des variables qui sont des suites (et non des nombres), ce qui évite l’usage de boucles ;
4. L’algorithmique, avec des sommes calculées par boucles, donc un esprit un peu différent des autres méthodes.

Pour chacune des démarches, le présent exercice peut être considéré comme une prise en mains de l’outil, en vue d’une utilisation ultérieure de celui-ci dans un contexte où il est plus approprié, voire de plusieurs outils, pour préparer l’élève au choix de l’outil adéquat pour un TP donné.

Sujet

Le sujet du TP est téléchargeable ci-dessous, sous licence CC :

This work is in the Public Domain.