La résolution d’équations du type $f(x)=0$ par la méthode de Newton est présentée en général par l’idée géométrique suivante :

• On remplace $f(x)$ par son approximation affine $f(a)+(x-a)f’(a)$, ou la représentation graphique de $f$ par sa tangente en $(a ;f(a))$ ;
• On a une équation facile à résoudre ($f(a)+(x-a)f’(a)=0 \Leftrightarrow x=a-\frac{f(a)}{f’(a)}$) mais fausse, la tangente n’étant pas suffisamment proche de la courbe.
• Mais on peut recommencer, obtenant ainsi une méthode itérative (un algorithme...) qui converge vers une des solutions de l’équation $f(x)=0$.

Côté programmation, on est amené à itérer la fonction $x-\frac{f(x)}{f’(x)}$ qui converge plus vite que les suites adjacentes de la méthode de dichotomie mais est plus difficile à calculer en raison de la présence de la dérivée (à évaluer par exemple numériquement...)

Scoop : On peut faire tout ça sans calcul de dérivée, en opérant comme Newton, avec une figure :

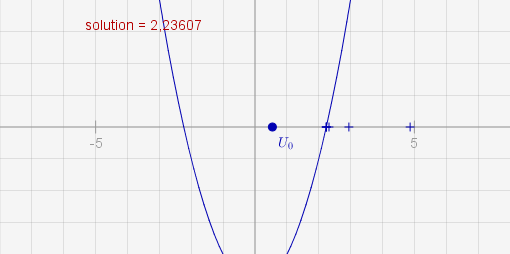
L’exemple ci-dessus, qui cherche à calculer $\sqrt{5}$ en résolvant l’équation $x^2-5=0$, revient donc dans le cas présent à la méthode de Heron [1].

La possibilité de bouger le point $U_0$ est intéressante, parce qu’elle permet de voir comment sa valeur détermine vers quelle solution de l’équation $f(x)=0$ la suite va converger. On peut simplement changer la fonction $f(x)$ en bas à gauche pour résoudre une autre équation. Et on peut créer la construction en appliquant une demi-douzaine de fois une macro, et en construisant vraiment la tangente, et sans calculatrice.

Voici une manière possible :

1. À partir de $U_0$, mener la parallèle à l’axe des ordonnées ;
2. Construire l’intersection de la droite verticale et de la courbe.
3. Mener par ce dernier point, la tangente à la courbe.
4. Enfin, construire l’intersection de la tangente et de l’axe des abscisses.

Puis cacher les traits de construction (sinon on aura vite fait de ne plus rien voir). Ensuite, on définit une macro avec pour objet initial, $U_0$, et pour objet final, le point qu’on vient de construire. Il suffit d’appliquer cette macro 5 fois de suite pour avoir une bonne approximation de la limite de la suite (l’abscisse du dernier point construit).

Comme il peut être difficile d’appliquer la macro à des points qui deviennent dangereusement rapprochés, on peut automatiser la construction avec les listes de GeoGebra ou avec un CaRScript :

Si on souhaite quand même renoncer au calcul graphique et implémenter l’algorithme sous forme numérique ou dans un tableur, on est obligé de précalculer la dérivée. Ici la dérivée de $x^2-5$ est $2x$ mais si par exemple on veut calculer le plus petit Nombre de Pisot-Vijayaraghavan avec $f(x)=x^3-x-1$, on a $f’(x)=3x^2-1$, calcul à refaire. On se retrouve donc avec un nouveau programme ou une nouvelle feuille de tableur pour chaque équation à résoudre. Sauf si le tableur a des fonctionnalités de calcul formel, comme par exemple Xcas :

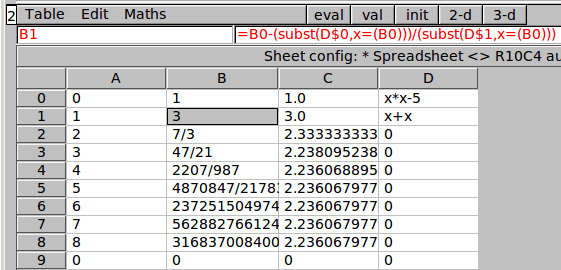
Ici la cellule D1 contient =diff(D0,x) et la cellule B0 contient 1.

La cellule B1 contient
=B0-subst(D$0,x=B0)/subst(D$1,x=B0)

Et comme la colonne B contient des fractions (calcul formel oblige), pour voir la convergence de la suite, on a mis dans C0 un =evalf(B0) qui a été recopié vers le bas.

On remarque que le choix a été fait ici d’une boucle effectuée 8 fois, plutôt qu’une boucle à condition de sortie qui eût été plus appropriée ici. Ce choix a été rendu possible par la vitesse de convergence de la suite.

Voici donc le plan d’une séquence de TP d’une heure autour de la méthode de Newton :

1. Faire faire la construction sous CaRMetal ou GeoGebra ;
2. faire construire une macro (sous CaRMetal) ou un outil (sousGeoGebra) à itérer environ 5 ou 6 fois.
3. Demander l’abscisse du ou des dernier(s) point(s) construit(s).
4. Si le temps le permet, refaire l’activité avec le tableur (xcas ou autre, mais dans ce dernier cas avec un calcul prélable de la dérivée). La justification de la formule $x=a-\frac{f(a)}{f’(a)}$ peut être faite dans l’énoncé du TP, voire en DM avant le TP.

Une approche similairement graphique de la méthode d’Euler (qui est d’ailleurs un algorithme) est visible dans ce tutoriel.