Le précédent article sur l’implémentation de la géométrie hyperbolique dans CaRMetal, s’il présentait les premiers objets fondamentaux de la géométrie, était aussi centré sur leur découverte dans un contexte d’investigation, avec comme objectif de montrer, in vivo, à de futurs enseignants la difficulté que ressentent les élèves de collège face à la démarche hypothético-déductive.
En conséquence, même si nous avons démontré un premier théorème absolu, à la manière de ce qui se fait en collège, nous n’avons pas véritablement abordé de constructions significatives dans cette géométrie. Par ailleurs nous avons abordé - essentiellement de manière opérationnelle - la notion de pinceau de droites. C’est surtout cette notion que nous allons développer ici, mais cette fois-ci de deux points de vue, d’un point de vue que l’on pourrait qualifier encore du monde sensible, par manipulation dans le modèle hyperbolique, puis d’un point de vue théorique et axiomatique.
Les choix de la présentation
Ce choix d’une approche d’abord expérimentale, même si elle construit de bonnes représentations des objets en jeu, peut ne pas satisfaire certains lecteurs. Ce choix s’inscrit pourtant dans une logique historique de ce que Gonseth a appelé une double axiomatisation.
Ce paragraphe reprend partiellement et développe une réflexion déjà proposée il y a quelques années sur le thème interprétations et modèles, et plus spécifiquement la partie 5 de cet article.
Comme enseignant, formateur d’enseignants du premier et second degré, cette description de la double axiomatisation est très parlante aussi bien à l’école primaire qu’en formation des enseignants.
La question soulevée est celle de du passage (et plus exactement de la circulation permanente) entre d’une part la voie effective de la découverte (que Gonseth associe au ratio essendi - la raison d’être, et la voie de la reconstruction formelle, alors associée au ratio cognoscendi - la raison du connaître. Dans ce contexte, la première correspond à la première axiomatisation de Gonseth, et la deuxième à la seconde axiomatisation, et ceci, à tous les niveaux de l’apprentissage.
En effet, à l’école primaire, la première axiomatisation associée à cette ratio essendi se fait dans les attitudes de dépersonnalisation et de décontextualisation de ces découvertes, dès le cycle 2 (CP-CE1) éventuellement, alors que la seconde axiomatisation à ce niveau scolaire, se fait (au cycle 3, en particulier au CM1-CM2) dans la conceptualisation des objets géométriques associés (parallélisme, orthogonalité, le rectangle, le carré comme cas particulier du rectangle alors qu’avant il s’agissait de deux formes différentes).
Au collège, la description de manière conceptuelle d’activités du monde sensible (pliage et autres exercices sur les symétries, les relations entre parallélisme et orthogonalité), avec un vocabulaire géométrique précis, relève d’une démarche de première axiomatisation, dès la classe de 6e. Le passage à la démarche hypothético-déductive de la fin du collège s’inscrit dans une seconde axiomatisation puisque l’on travaille sur les relations mathématiques entre les objets construits sur la première.
En formation des enseignants, outre l’expérience personnelle de chaque étudiant dans cette circulation entre les deux niveaux, d’une manière plus institutionnelle, la première axiomatisation se place dans l’apprentissage de gestes professionnels pour la présentation de la géométrie au collège avec ses propres outils (les leçons de préparation à l’oral du CAPES par exemple en sont une bonne illustration), alors que la formation mathématique initiale des étudiants, véritable ratio cognoscendi de leur vécu géométrique avec l’intégration des structures algébriques et vectorielles en est une seconde axiomatisation, et correspond à la demande institutionnelle pour la partie écrite du concours.
Nous allons faire un peu la même chose dans cet article : une première partie d’exploration mathématique dans le modèle de Poincaré de la géométrie hyperbolique, et plus particulièrement des pinceaux, ce sera notre première axiomatisation, et une seconde partie qui, par une algébrisation complète de ce qui vient d’être présenté, en sera une seconde axiomatisation.
C’est aussi, comme formateur, parce que cette seconde axiomatisation est si aboutie, si formellement belle, que j’ai choisi de l’introduire de manière opérationnelle, en manipulant d’abord les concepts en jeu, afin de construire de bonnes images mentales préalables - en tout cas hyperboliques sinon génériques - qui permettront d’accompagner cette présentation et d’entrer probablement plus facilement dans l’axiomatique de Bachmann, pour celles et ceux que cette seconde partie intéressera.
Aller directement à la partie 2 (pour la reconstruction formelle de la géométrie plane)
Première partie - Exploration des pinceaux dans un modèle hyperbolique
Nous reprenons notre approche empirique des pinceaux de droites. Dans le précédent article nous avions vu qu’il y avait deux notions, celle de « trois droites en pinceau » - ce sera le cas des droites « remarquables » d’un triangle - et celles des « pinceaux de droites » et que nous jouions, dans le discours mathématique, sur les relations implicites entre les deux notions.
Trois droites sont en pinceau si elles ont quelque chose en commun, à savoir - nous sommes dans la voie de la découverte - un point hyperbolique, une perpendiculaire, ou un point idéal.
Comme c’est présenté,
– c’est indépendant de l’ordre des droites,
– les trois types de pinceau associés sont (empiriquement/implicitement) disjoints, alors que c’est au cœur même de la spécificité hyperbolique que de séparer les pinceaux à axe des pinceaux sans support.
Deux droites a et b définissent le pinceau P(ab) : c’est l’ensemble des droites c telles que a, b, et c sont en pinceau. Le pinceau est noté P(ab) car il ne dépend que du produit des droites.
Si a et b
– sont sécantes : on parle de pinceau à centre,
– ont une perpendiculaire commune : on parle de pinceau à axe,
– ont un point idéal commun : on parle de pinceau sans support (car le support n’appartient pas à la géométrie).
On pourrait constater - se fera dans l’introduction à la seconde partie - que la composée des symétries orthogonales de trois droites en pinceau est une symétrie orthogonale (ce qui sera à la fois la définition théorique des droites en pinceau et l’essentiel des axiomes de tri-réflexions de Bachmann) et que c’est une droite du pinceau (ce sera un théorème).
Plus implicite, car jamais vraiment formalisé dans cette phase de première axiomatisation, est le statut de représentant du pinceau de la paire des deux droites a et b. Autrement dit le fait que si u et v sont deux droites de P(ab), alors P(uv) = P(ab). Cette partie là est non triviale à montrer dans le cas général, ce sera le théorème de transitivité.
Organisation des onglets de cette première partie
• 6 outils : description de la nouvelle ligne d’outils de CaRMetal, avec mise en œuvre, réflexions empiriques (de première axiomatisation) et applications immédiates.
• Triangle orthique : c’est l’occasion d’illustrer (sera démontré dans la deuxième partie) que certaines propriétés élémentaires que l’on démontre généralement avec de la trigonométrie dans le contexte euclidien sont en fait générales aux trois géométries de base.
• Bissectrices : ce sont les « droites remarquables » les plus délicates. En particulier pour les trilatères, elles existent mais ne sont pas nécessairement en pinceaux. Des propriétés spécifiques seront examinées, et certaines seront montrées ensuite dans le cadre théorique.
• La propriété de Gergonne et la
• Construction de Malffati seront illustrées dans le cas général des trilatères, en particulier « Malfatti » se construira par une lecture « absolue » et « en pinceaux » de la construction euclidienne. Cette construction sera l’occasion d’aborder la question de la « désorientation » des figures continues mais orientées.
Les 6 outils
Six outils sur les pinceaux (à partir de CaRMetal 3.6.5)
La nouvelle palette des constructions hyperboliques est désormais celle-ci :

plus précisément, elle s’est enrichie d’une nouvelle ligne (la 6°) avec des icônes un peu ésotériques, sur les pinceaux, dans une représentation euclidienne conforme à la palette et à l’esprit du logiciel. En pratique, les petites croix sont en fait deux droites qui représentent un pinceau.
Les bulles de commentaires rendent les choses au début plus explicites, et ensuite à l’utilisation, cela devient très clair. Pour une première lecture, dans les présentations des outils, nous avons placé une illustration dans le contexte du modèle du disque de Poincaré.


La présentation de cet onglet détaille chaque outil, propose éventuellement une première réflexion quant à son objet. Cette réflexion peut par exemple chercher à justifier (ou discuter) l’existence dans tous les cas de pinceaux possibles (ce qui correspond à la phase de première axiomatisation) alors que l’outil lui-même est clairement construit autrement : sa construction, ne pouvant être impliquée par la typologie des pinceau, utilise d’autres considérations qui peuvent être théoriques et/ou liées au modèle hyperbolique utilisé. Parfois, pour aider à construire de bonnes représentations, une première réflexion sur l’existence de l’objet produit est proposée.
Droite d’un pinceau passant par un point
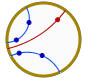
Étant données un pinceau (représenté par deux droites) et un point, cet outil construit la droite du pinceau passant le point. Voyons que la droite existe toujours et qu’elle est unique. En effet, si le pinceau est
– à centre, la droite existe, et elle est unique, c’est même un axiome d’incidence minimal : par deux points distincts il passe une droite et une seule.
– à axe, il passe par ce point une perpendiculaire (unique) à cette droite (l’axe) donc la droite existe et est unique.
– sans support : dans notre modèle, cela veut dire que les deux droites passent par un même point idéal I : il est alors facile de construire la droite hyperbolique passant par I et le point donné.
On voit donc bien qu’en déclinant chaque types de pinceau, cette droite existe et est unique.
Mais ce raisonnement relève à la fois du monde sensible hyperbolique mais aussi de sa modélisation. Il invite donc à deux remarques :
– le cas « sans support » n’est réglé que dans le modèle, il n’est pas du tout abordé dans le cadre de la géométrie hyperbolique. Ainsi, Bolyaï ou Lobatchevsky, dans leurs constructions de la géométrie hyperboliques, ont dû, pour leur raisonnement général, proposer des construction internes à la géométrie hyperbolique - avant toute pensée même qu’il puisse exister un modèle euclidien de cette géométrie - pour construire la demi-droite passant par un point et parallèle à deux demi droites parallèles données. (On comprend bien qu’ils devaient travailler sur les demi-droites car une droite a deux extrémités, et c’est pour cela que par un point il passe deux parallèles à une droite donnée : une demi-droite par extrémité.
– le cas « à axe » s’il est naturel est lui aussi traité avec un peu de rapidité : on suppose - on veut - que dans cette géométrie là, par un point il passe une, et une seule, perpendiculaire à une droite donnée. Cela sera montré, mais ce n’est en rien une évidence. Il existe des géométries non euclidiennes, qui comme l’hyperbolique ne sont différentes de l’euclidienne que par un seul axiome mais dans laquelle pour chaque droite (sauf cas particulier) il existe une partie du plan telle que d’aucun point de cette partie on ne peut mener de perpendiculaire à cette droite. C’est le cas du plan de Moulton, l’exemple minimal archétypique de la géométrie non arguésienne : figures en manipulation directe et définitions détaillées dans cette page (à ouvrir dans un nouvel onglet).
Comme il y a la construction d’une droite unique, c’est un premier outil « règle droite pinceau » qui est proposé là. On comprend bien que c’est un cas particulier de l’outil de la troisième icône qui va être une« règle pinceau-pinceau ». Mais ce cas particulier est important, d’une part parce qu’on peut toujours construire la droite, d’autre part, on va peu à peu le comprendre, l’existence d’un point, dans le monde des pinceaux, est toujours source de richesse et de simplification ...
Produit de trois droites en pinceau
Le fait que trois droites soient en pinceau est une propriété significative dans le contexte qui nous occupe. On a vu par exemple, dans le précédent article consacré aux premiers outils hyperboliques, que c’est le cas de toutes les droites remarquables d’un triangle. Ici on s’intéresse au produit. Qu’est-ce que le produit de trois droites ?
C’est l’occasion, comme on le disait dans l’introduction, de circuler entre les deux niveaux d’axiomatisation. Le terme produit nous propulse effectivement dans une structure algébrique alors que nous parlons de droites, donc des objets premiers d’une géométrie. L’objet algébrique associé à la droite est la symétrie orthogonale associée à cette droite. Le produit de trois droites signifie donc, d’un point de vue algébrique, la composée de ces symétries orthogonales. La seconde axiomatisation va être fondamentalement algébrique, ses objets premiers seront des éléments d’un groupe, et plus particulièrement des éléments d’ordre 2. Aussi ces outils du logiciel sont l’occasion de voir que tout en manipulant des objets de la première axiomatisation - des droites dans un modèle - on peut en même temps travailler dans un autre niveau de vocabulaire et de structure.
Qu’est-ce que le produit de 3 droites en pinceau ? C’est une droite - c’est même la définition initiale d’être en pinceau - et c’est ce que rend cet outil. Ce sera un axiome pour les pinceaux à centre et à axe, et ce sera une conséquence pour les autres pinceaux.
Puisque les droites correspondent à des symétries orthogonales, d’un point de vue algébriques, ce sont des éléments d’ordre 2, donc égaux à leur inverse. autrement dit, faire le produit abc ou le produit cba donne le même résultat car le second est l’inverse du premier, chaque élément étant son propre inverse :
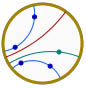
C’est ce qu’on illustre dans la figure suivante en construisant le produit (rouge) des deux droites bleues (a et c) et de la droite cyan (b). La macro s’applique ainsi : on montre les droites dans l’ordre a, b, c, pour faire le produit abc. On notera aussi que la droite verte a été obtenue par l’outil précédent.

On voit que le produit des trois droites en pinceau est une droite du même pinceau. Ce sera une conséquence des axiomes.
Bien entendu, les autres ordres que l’inverse produisent d’autres droites, voici par exemple les autres permutations circulaires sur a, b, et c.

Sur cette figure, il semble que des droites soient des bissectrices d’autres droites. Par exemple on voit clairement que a est bissectrice de bca et abc. On voit moins que c est bissectrice de abc et cab mais pour des raisons de symétrie, on imagine bien que c’est le cas. Reste b qui est - ne peut être que - bissectrices des droites bca et cab.
Remarque : pour le vérifier expérimentalement, on pourrait rendre le pinceau défini par les droites a et b à centre et utiliser les mesures des angles.
On peut tenter de poursuivre cette circulation entre les deux niveaux d’axiomatisation, mais si le lecteur a envie de ne pas suivre, c’est sans incidence pour la suite de la présentation des outils. (bloc suivant éventuellement réservé à une seconde lecture)
On vient de dire que que a est bissectrice de bca et abc, autrement dit : $s_a(abc) = cba$ , mais comment s’exprime, algébriquement, cette action géométrique de la symétrie $s_a$ ?
On peut remarquer $a(abc)a = bca$. Et de même pour les autres bissectrices $c(abc) c = cab$ et encore $b(bca)b = cab$.
Autrement dit, comme les droites sont égales à leur inverse, on voit que l’action d’une droite sur un objet est la conjugaison. Ou plus exactement, si la transformation géométrique d’une isométrie s’exprime comme la conjugaison dans le groupe des transformations (il reste encore de nombreuses choses à préciser), alors les propriétés de bissectrices des droites évoquées plus haut sont montrées simplement par les relations précédentes.
Or voyons que c’est bien le cas, déjà dans le cas euclidien : si $A’=s_d(A)$ alors $A’=dAd=dAd^{-1}$.
Pour cela regardons (géométriquement) l’image d’un point M par les deux transformations :
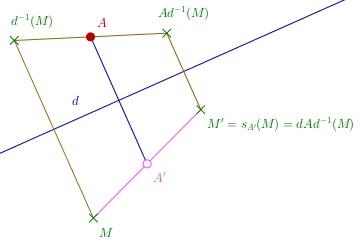
Ainsi une algébrisation ultime de la géométrie, où les objets premiers de la géométrie vont être des objets algébriques (éléments d’un groupe) va pouvoir s’exprimer en utilisant comme action des isométries, l’action de groupe la plus simple qui soit : la conjugaison.
On peut comprendre un peu mieux, avec ce simple exemple de l’expression algébrique de l’image d’un point par une symétrie, le fossé qu’il peut y avoir entre un niveau d’axiomatisation et le suivant, et la difficulté que peut rencontrer un élève ou un étudiant à suivre son enseignant, à quelque niveau d’enseignement qu’il soit, du CE1 à la licence, qui circulerait sans précaution d’un niveau à l’autre alors que cette circulation là est souvent l’objectif même de son enseignement.
Intersection de deux pinceaux

Même si le second outil est plus conceptuel dans sa présentation, les deux premiers outils déjà vus ont ceci de commun qu’ils produisent une droite qui existe toujours. Nous abordons maintenant deux nouveaux outils qui vont encore produire une droite mais qui pourra ne pas exister dans certains cas particuliers
L’intersection de deux pinceaux P(a,b) et P(c,d) est une droite qui appartient aux deux. Il y a six cas de figure :
– les deux pinceaux sont à centre, la droite existe et elle est unique, c’est un axiome d’incidence.
– les deux pinceaux sont à axe : la seule droite possible est la perpendiculaire commune aux deux axes de ces pinceaux.
– les deux pinceaux sont sans support : il y a deux points idéaux : il existe une unique droite ayant ces deux points idéaux.
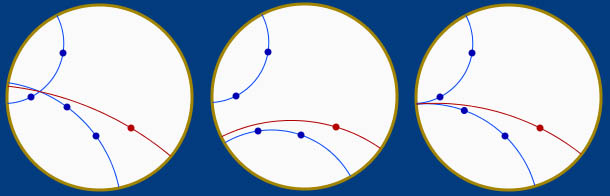
Ces trois premiers cas sont illustrés dans le montage suivant :
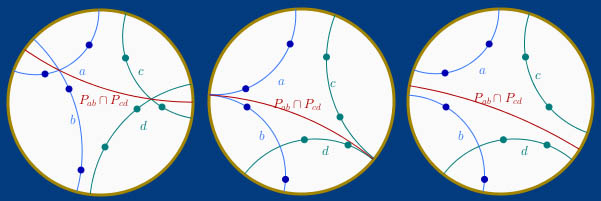
Reste trois cas :
– un pinceau est à centre , l’autre à axe : c’est l’existence d’une perpendiculaire à une droite issue d’un point donné.
– un pinceau est à centre, l’autre sans support : c’est l’existence d’une droite appartenant à un pinceau issue d’un point donné (traité dans le premier outil)
– un pinceau est à axe l’autre sans support : c’est d’une part, sur un cas particulier (axe), l’extension du premier outil au cas où le point est à l’infini. Mais c’est aussi l’existence d’une perpendiculaire à une droite donnée ayant une direction donnée à l’infini, ce qui est assez éloigné des représentations euclidiennes.
Les cas particuliers où la droite des pinceaux n’existe pas
Le cas particulier le plus courant est celui où les pinceaux sont tous les deux à axe. La droite d’intersection des deux pinceaux (qui est alors la perpendiculaire commune aux deux axes) ne peux exister que si les deux axes ne sont ni parallèles ni sécants :

puis à droite ils sont sécants. Dans ces deux cas là, il n’y a pas de droite solution.
Un autre cas particulier est plus anecdotique. C’est celui où un pinceau - disons P(a,b) - est sans support, et l’autre est à axe avec cet axe appartenant à P(a, b).

Utilisation effective
Cet outil s’utilise en cliquant d’abord sur les deux droites représentant le premier pinceau puis les deux droites représentant le second pinceau.
Comme le premier outil, celui-ci est encore une extension du concept de règle : il créé, quand elle existe, la droite passant par deux pinceaux donnés.
Et la nuance avec le premier outil est d’importance : avec un point, cette droite existe toujours, sans point, elle peut ne pas exister. Cette nuance sera toujours présente dans toutes les figures : dans la géométrie des faisceaux, la présence d’un point est une donnée précieuse en soi : elle assure souvent une existence.
Note pratique : dans une construction complexe, même si on sait que deux pinceaux sont à centre, il est parfois plus judicieux d’utiliser cet outil d’intersection de deux pinceaux que la simple droite passant par deux points.
Perpendiculaire à une droite issue d’un pinceau

La perpendiculaire à une droite issue d’un pinceau peut être vue de deux façons différentes, soit :
– comme une extension de la notion de perpendiculaire à une droite issue d’un point, ce point matérialisant un pinceau à centre.
– comme un cas particulier de l’intersection de deux pinceaux, l’un d’eux - celui qui est représenté par la droite - étant toujours à axe (son axe étant cette droite).
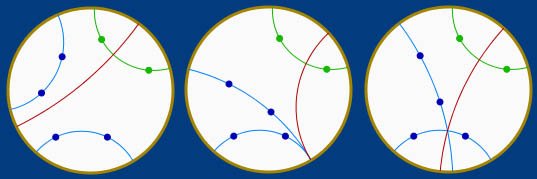
Cas où la perpendiculaire n’existe pas
Dans la seconde présentation, on vient de voir à l’outil précédent que si le pinceau est à axe, la perpendiculaire peut ne pas exister. En particulier elle n’existe pas si l’axe du pinceau coupe la droite.

Les hauteurs d’un trilatère
On appelle trilatère un ensemble de trois droites qui ne sont pas en pinceau. L’outil perpendiculaire issue d’un pinceau permet de construire le hauteurs. On montre que si les hauteurs d’un trilatère existent, alors elles sont en pinceau. Mais en terme d’existence on peut rencontrer toutes les situations comme par exemple :
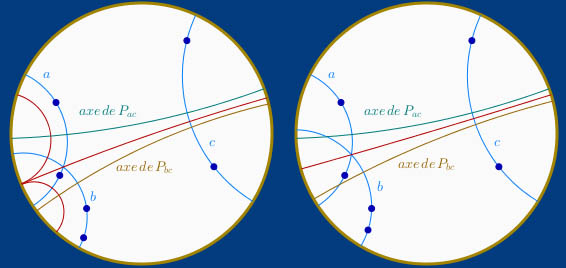
On voit que l’axe de P(b,c) est proche de couper la droite a et l’axe de P(a, c) assez proche de la droite b.
À droite ces deux axes coupent les droites respectives et deux hauteurs ne peuvent exister.
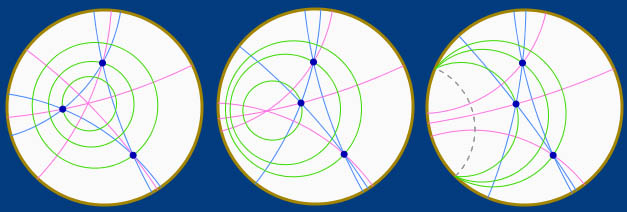
Dans l’illustration suivante on a,
– à gauche, le cas usuel d’un trilatère avec ses trois hauteurs en pinceau, de plus ici à centre, et donc avec un orthocentre,
– à droite un trilatère n’ayant aucune hauteur.

Dans l’onglet suivant, on reviendra sur les trilatères ayant leurs trois hauteurs, car dans ce cas il existe des points : les pieds des hauteurs, et donc un triangle intéressant ...
Cycle défini par un pinceau et passant par un point
Cet outil est une illustration de l’extension du de concept de cercle à celui de cycle, comme défini dans l’article précédent sur la géométrie hyperbolique, si le cercle est l’image d’un point par un pinceau à centre.
A partir d’un pinceau (deux droites) et d’un point, on défini ainsi un cycle qui est, géométriquement, un cercle une équidistante ou un horicycle selon que le pinceau soit, respectivement, à centre, à axe ou sans support.
Dans le modèle du disque de Poincaré, c’est un cercle ou un arc de cercle, et pour l’horicycle, un cercle privé d’un point que l’on appelle aussi son centre.
En terme de mise en œuvre, on aborde la question de la limite de l’implémentation dynamique d’un concept abstrait dans un modèle, quand ce concept se représente par deux objets différents.

par le point défini par le pinceau. (La macro construit également l’axe du pinceau s’il existe)
L’illustration précédente peut faire illusion, avec le même nom donné au cycle dans deux configurations de pinceaux différents. En réalité le logiciel construit deux objets différents, le cercle et l’arc de cercle, il n’y a pas unité de la représentation alors qu’il y a unicité du concept mathématique représenté : cycle défini par un pinceau et un point.
C’est un exemple d’une des limites de la représentation dans un modèle, où il faut tenir compte du modèle. En pratique si on prend un point sur objet du cycle, dans sa construction dynamique, ce point n’existera que dans une des configuration.
D’un autre côté, un outil comme le produit de trois droites - avec trois droites du pinceau, donne un objet premier de la géométrie - une droite - qui a souvent une propriété spécifique de la construction, invariante par rapport au type de pinceau, ce qui permet de continuer à faire des figures encore génériques, nous y reviendrons dans les prochains onglets.
a) il n’y a pas à construire l’orthocentre s’il existe
b) au contraire la construction par cet outil est plus générale
Compléments sur les représentations dans les modèles
Le cycle défini par un pinceau et un point, a un rapport différent à l’infini, selon le type de pinceau : selon que le cycle soit à centre, sans support, à axe, il a 0, 1 ou 2 points de contact avec l’infini. En ce sens, la représentation par un cercle ou arc de cercle - dans le modèle qui nous occupe - va correspondre à un cercle sans contact, tangent ou sécant au cercle horizon, en particulier parce que deux cercles distinct ne peuvent avoir deux points de contact.
La représentation dans un autre modèle peut produire une situation plus simple. Par exemple dans le modèle de Klein-Beltrami (KB), les cycles sont représentés par des ellipses qui peuvent être intérieures, tangentes ou bitangentes au cercle horizon : la continuité dynamique de la représentation, d’une certaine façon, serait plus simple dans le modèle KB.
Note technique : on évitera d’utiliser cet outil quand on sait que le pinceaux est explicitement sans support : la construction n’est pas stable (on passe dynamiquement du cercle à l’équidistante).
Bissectrice de deux droites orientées

Ce dernier outil sur les pinceaux est plus long à utiliser. En effet, dans son implémentation, nous avons choisi d’incorporer le traitement de la continuité de la droite produite. On sait que deux droites non sécantes ont un seul axe de symétrie, alors que deux droites sécantes ont deux axes de symétrie. La question se pose donc de la continuité de cette bissectrice quand on passe d’un type de pinceau à l’autre, et de la conservation de cette continuité, tout en respectant le déterminisme de la figure. Or on sait que sur un plan théorique, continuité et déterminisme sont souvent antagonistes - et ils le sont ici. Cela signifie qu’arriver à respecter les deux a nécessairement un prix par ailleurs. C’est ce que nous allons voir rapidement, mais commençons par décrire l’utilisation de cet outil.
Mode d’emploi de l’outil
Dans un premier temps on ne part pas de droites ordinaires, mais de droites orientées (l’outil double flèche de la cinquième ligne). Une droite orientée (AB) renvoie ses points idéaux Ia et Ib qui sont tels que Ia, A, B et Ib sont toujours dans cet ordre. C’est la prise en compte de cet ordre qui permet la continuité de la bissectrice dans la manipulation directe des objets géométriques.
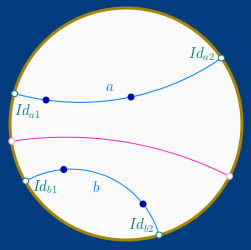
Il faut montrer la droite a, ses points idéaux Ida1, Ida2, la droite b, ses points idéaux Idb1, Idb2
L’outil renvoie une (la) bissectrice, elle aussi orientée
L’orientation de la figure comme prix de la continuité "déterminée"
Puisque les droites sont orientées et que cette orientation est utilisée pour construire la bissectrice, le prix à payer est facile à imaginer (au moins théoriquement), c’est celui d’une figure "orientée". Une figure orientée ? Voyons cela sur le simple exemple de l’application même de l’outil.
On part, en haut à gauche de l’illustration suivante, de la bissectrice de deux droites en pinceau à axe. On voit au centre que l’on poursuit cette bissectrice quand le pinceau devient à axe.
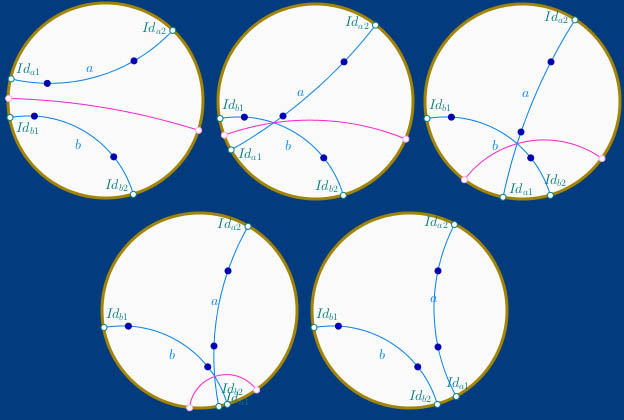
Alors l’angle croît à partir de l’angle nul (qui correspond au pinceau sans support) et peut dépasser l’angle droit, devenir obtus. La question de la continuité en manipulation directe consiste à maintenir la construction de la même bissectrice comme on le voit à droite et sur l’illustration de gauche de la seconde ligne d’illustrations.
La dernière illustration montre le prix à payer pour cette continuité et ce déterminisme réalisés conjointement : la figure est orientée.
Cela signifie que, dans l’orientation donnée au départ, il n’y a pas de bissectrices des deux droites dans cette configuration (ie avec cette position des points idéaux inversés). Si on veut faire une figure dans ce cas (et on le fera dans l’onglet Malffati pour montrer ce qu’il est possible de faire), il faudra un processus pour inverser l’orientation de l’une des droites.
On voit donc qu’il y a bien un inconvénient à ce choix, mais, après de nombreux tests, il apparaît clairement que, pour la manipulation directe, la transformation d’une figure en figure orientée (qui doit toujours restée présente à l’esprit) est un prix moindre que la non continuité de la bissectrice.
Les bissectrices d’un trilatère
On a vu que les hauteurs pouvaient ne pas exister mais que si elles existent, elles sont en pinceau. Pour les bissectrices c’est différent : les bissectrices existent toujours mais elles sont les seules droites "remarquables" de la géométrie euclidiennes qui peuvent ne pas être en pinceau.

Sur la figure précédente les droites initiales sont bleues, les bissectrices roses, et les perpendiculaires communes des bissectrices vertes prises 2 à 2 : elles sont distinctes, ce qui signifie que les bissectrices ne sont pas en pinceau
En fait il y a une condition suffisante très significative : si deux bissectrices d’un trilatère sont sécantes, alors les trois bissectrices sont nécessairement en pinceau. Là encore, l’existence d’un point est structurant. Mais sans cela, il y a d’autres résultats intermédiaires. Nous y reviendrons plus longuement.
Les onglets suivants vont être l’occasion de mettre en œuvre ces outils.




Commentaires