Définition de la notion de tangente dans un contexte mathématique restreint au programme de Seconde
Étant données une droite d’équation y = ax + b et une courbe d’équation y = f(x),
lorsque l’équation en x qui traduit la recherche de leurs points communs, à
savoir ax + b = f(x), se ramène, après réduction, à une équation du second degré en x qui s’écrit (à un facteur non nul près) sous la forme (x – t)2 = 0, où t est un nombre réel, la droite est dite tangente à la courbe au point d’abscisse t.
On interprète cela en disant que la droite coupe la courbe en deux points confondus. Le point commun (t, f(t)) est appelé point de contact .
Un segment est dit tangent à une courbe lorsque la droite qui le porte est
tangente à cette courbe et que le point de contact est sur le segment.
La notion de tangente sera reprise, améliorée et complétée en classe de 1re (et au delà) dans le cadre de l’étude systématique de l’équation du second degré et de la notion de dérivée (et plus tard de la notion de courbe).
Réalisation pratique et artistique
Les segments [AB] prennent un nombre fini de positions [AuBu]. On réalise la figure restreinte aux seuls points Au, Bu sur papier.
On prépare une planche de contre-plaqué peinte en couleur sombre (noir mat par
exemple) suffisamment grande pour pouvoir y coller avec du scotch la figure papier ou mieux sa copie.
Sur la dite planche, on plante un petit clou à tête homme en chaque point Au et en chaque point Bu. On élimine la figure papier (ce qui a pour effet de la déchirer). Enfin, pour chaque u, on tend un fil de couleur claire entre Au et Bu.
Pour parachever son chef-d’oeuvre, l’artiste le signe, puis il l’expose en l’accrochant au mur.
Problème 1 : cas où la somme des distances est constante
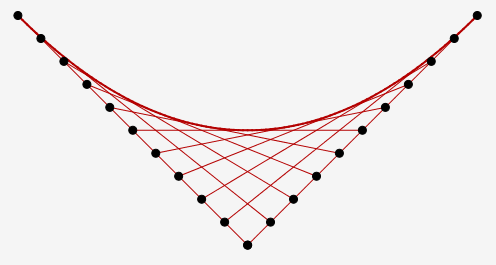
On commence à réaliser un repère orthonormé avec pour unité 1 cm sur une feuille de papier format A4 (21,0 cm x 29,7 cm) quadrillée de carreau 0,5 cm de côté. On place les axes de façon à pouvoir effectivement graduer l’axe des abscisses entre –10 et +10, l’axe des ordonnées entre 0 et +10, et à avoir un bonne mise en page.
On définit, à l’aide de leurs coordonnées, onze points Au et onze points Bu numérotés par l’indice entier relatif u de –5 à +5.
| A–5 (–10, 10) | B–5 (0, 0) |
| A–4 (–9, 9) | B–4 (1, 1) |
| A–3 (–8, 8) | B–3 (2, 2) |
| A–2 (–7, 7) | B–2 (3, 3) |
| A–1 (–6, 6) | B–1 (4, 4) |
| A0 (–5, 5) | B0 (5, 5) |
| A1 (–4, 4) | B1 (6, 6) |
| A2 (–3, 3) | B2 (7, 7) |
| A3 (–2, 2) | B3 (8, 8) |
| A4 (–1, 1) | B4 (9, 9) |
| A5 (0, 0) | B5 (10, 10) |
1. Représenter soigneusement les points Au, Bu et les segments [AuBu].
2. Ainsi, Au a pour coordonnées (–5 + u, 5 – u) et Bu a pour coordonnées (5 + u, 5 + u). Vérifier que les points Au d’une part, Bu d’autre part, sont alignés sur une demi-droite d’origine O, à préciser.
Évaluer la somme OAu + OBu. Est-elle bien constante ?
3. Rechercher les équations des droites (AuBu), on commencera par rechercher leur pente en fonction de u.
4. On propose comme courbe tangente à toutes ces droites, la courbe représentative d’une fonction paire polynômiale du second degré : y = cx2 + d,
où c non nul et d sont des coefficients réels à déterminer.
Exprimer que la droite (A0B0) est tangente à cette courbe, en déduire d.
1er cadeau : si on n’a pas fait d’erreur, on trouve d = 5.
Exprimer que la droite (A5B5) est tangente à cette même courbe, en déduire c.
2e cadeau : si on n’a pas fait d’erreur, on trouve c = 1/20.
On appelle désormais P la courbe obtenue.
5. Vérifier que toutes les droites (AuBu) sont tangentes à P.
Indication : tout réduire au même dénominateur 20.
Préciser les coordonnées des points de contact, vérifier qu’ils sont bien sur les segments [AuBu], les placer sur la figure, enfin tracer la courbe P.
Problème 2 : cas où le produit des distances est constant
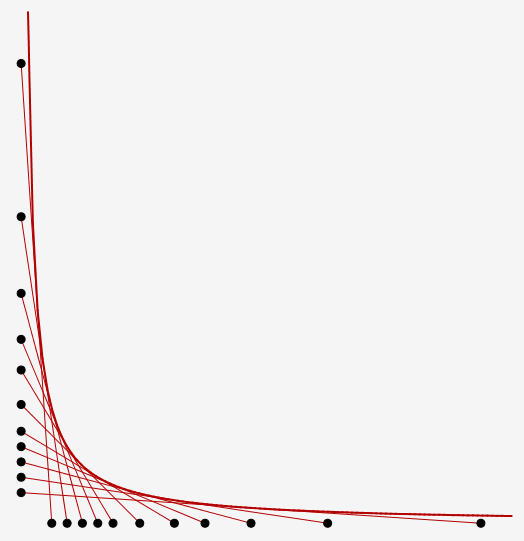
On commence à réaliser un repère orthonormé avec pour unité 0,5 cm sur une feuille de papier format A4 (21,0 cm x 29,7 cm) quadrillée de carreau 0,5 cm de côté. On place les axes de façon à pouvoir effectivement graduer l’axe des abscisses entre 0 et +30, l’axe des ordonnées entre 0 et +30 et à avoir un bonne mise en page.
On définit, à l’aide de leurs coordonnées, onze points Au et onze points Bu indexés par le paramètre réel u > 0. Les points Au sont placés sur le premier axe d’abscisse 60/u. Les points Bu sont placés sur le deuxième axe d’ordonnée u. Le paramètre u prend les onze valeurs : 2, 3, 4, 5, 6, √60, 10, 12, 15, 20, 30.
1. Représenter soigneusement les points Au, Bu et les segments [AuBu].
2. Évaluer le produit OAu x OBu. Est-il constant ?
3. Rechercher les équations des droites (AuBu), on commencera par rechercher leur pente en
fonction de u.
4. On propose comme courbe tangente à toutes ces droites, la courbe représentative d’une fonction homographique restreinte à x > 0 : y = k/x, où k est un coefficient réel non nul à déterminer.
Exprimer que la droite (A√60B√60) est tangente à cette courbe, en déduire k.
Cadeau : si on n’a pas fait d’erreur, on trouve k = 15.
On appelle désormais H la courbe obtenue.
5. Vérifier que toutes les droites (AuBu) sont tangentes à H.
Préciser les coordonnées des points de contact, vérifier qu’ils sont bien sur les segments [AuBu], les placer sur la figure, enfin tracer la courbe H.




Commentaires