Il se trouve que B. Parisse, le créateur du logiciel xcas, donne un cours de climatologie et que donc plusieurs exemples concernant le réchauffement climatique sont fournis avec le logiciel xcas. Or faire faire des exercices sur la régression linéaire suppose beaucoup de temps pour entrer les données avant de discuter sur le bien-fondé de ladite régression. Avec ces exemples, xcas tombe à pic [1].
Donc dans un premier temps, xcas est lancé au TBI et l’exemple « vostok » chargé dans xcas. On y voit les deux courbes suivantes, représentant respectivement l’évolution de la température et celle de la teneur en CO2, dans le passé, obtenues à partir de carottes de glaces prélevées sur la station Vostok en Antarctique :

Réaction des étudiants : Il n’y a pas photo, le lien entre les données est évident. La veille, avait été fait le cours sur la méthode des moindres carrés et le coefficient de corrélation, et l’image suivante, représentant les mêmes données mais avec le taux de CO2 en abscisse et la température en ordonnée, a été littéralement réclamée par eux :
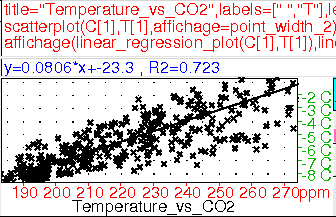
Là, on voit que la corrélation entre le taux de CO2 et la température de l’atmosphère n’est pas si nette que ça, ce que confirme le coefficient de corrélation dont le carré vaut 0,723 — ce qui n’est pas terrible.
La suite a été consacrée au seul taux de CO2 mais sur des données plus récentes mesurées au sommet du superbe volcan Mauna Loa de l’île d’Hawaii. Pour cela il a suffi de charger le fichier d’exemple « co2 », également fourni avec xcas, et qui montre la célèbre courbe que voici :
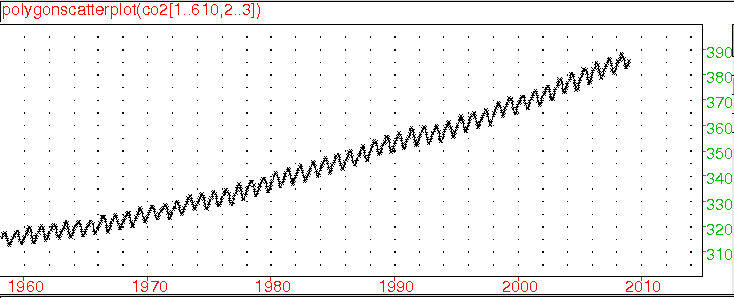
qui rappelle énormément le film Une vérité qui dérange.
Problème pour faire un exercice : Les données sont nombreuses et soumises à des variations saisonnières. Il a donc fallu les filtrer pour obtenir un exercice abordable en moins d’une heure (il a fallu environ 5 minutes pour montrer les données), ce qui m’a conduit à choisir les données de septembre (le minimum de chaque année) pendant 8 ans, de 2000 à 2008 :
| Année | taux de CO2 (ppm) |
| 2000 | 367 |
| 2001 | 368 |
| 2002 | 371 |
| 2003 | 373 |
| 2004 | 374 |
| 2005 | 377 |
| 2006 | 379 |
| 2007 | 381 |
| 2008 | 383 |
Après ça l’exercice fut plus classique :
- Donner la droite de régression : équation et représentation graphique.
- En déduire à quel moment le taux de CO2 aura dépassé 1000 [2].
- Calculer le coefficient de corrélation et en déduire la pertinence du modèle linéaire.
- Remplir le tableau ci-dessus avec les logarithmes des taux de CO2.
- Refaire l’exercice avec les nouvelles données.
Conclusion
L’exercice lui-même a été terminé à la fin de l’heure mais le fait de l’avoir précédé de l’exposé fait avec xcas a permis d’intéresser les étudiants à cet exercice (le sujet concerne tout le monde).

Commentaires