L’animisme est toujours présent chez certains élèves : Puisque JavaScript sait tout faire, on n’a qu’à lui demander de calculer le nombre d’œufs par quelque chose comme

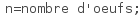
Au cours de l’année scolaire, cette attitude tend à disparaître mais assez lentement. L’utilisation de logiciels de calcul formel avec des pgcd tout faits constitue dans ce domaine une gêne pour ces élèves-là (s’ils poursuivent dans la voie scientifique).

Plusieurs élèves ont proposé une solution presque juste sauf que l’affichage du nombre d’emballages n’est pas fait dans le test mais après tout le script, ce qui donne une réponse de 201 :

La création d’une variable n avant la boucle (inutile car elle sera créée à nouveau dans la boucle) est arrivée aussi 2-3 fois :

Le fait que n=40 au début de la boucle est une affectation est en effet assez difficile à percevoir (ça ressemble quand même beaucoup à un test, non ? Surtout que après ça, c’est un test : La condition de sortie)

Lassé de ne pas réussir le TP, un élève a fait la même chose qu’en maths : Fabriquer un patchwork avec des notations ressemblant aux TPs précédents :

Le pire, c’est que CaRMetal n’affiche aucune erreur de syntaxe, puisque celle-ci est correcte (le programme affiche toutes les valeurs de l’indice ce qui lasse d’ailleurs assez vite son utilisateur). La logique sous-jacente est si difficile à imaginer qu’on peut très bien penser qu’il n’y a pas de logique du tout...

La traduction de « par 6, il en reste 2 » en

n%6==2

est apparemment évidente pour tous les élèves (il faut dire qu’une explication avait été donnée à l’issue d’un cours), mais la traduction de « par 8, il n’en reste pas » en

n%8==0

l’a été beaucoup moins, alors on a vu apparaître des n%8 traités comme des booléens (ça marche en raison d’une conversion automatique par JavaScript) qui sont après tout faux puisque tout nombre autre que 0 est considéré comme vrai en booléen. La correction

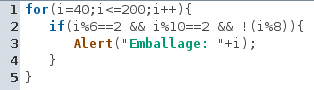
de cette « erreur » consiste à écrire « divisible par 8 » en la négation de « il reste quelque chose de non nul dans la division ». Cette production n’était évidemment pas du tout attendue des 2-3 élèves qui l’ont faite...

Puisque n est divisible par 8, la boucle peut être parcourue non pas de 1 en 1, mais de 8 en 8 (en effet 40 se trouve être un multiple de 8, ce qui n’est sans doute pas un hasard). Un seul élève a exploré cette voie mais il n’a pas remarqué que le test de divisibilité par 8 n’est pas nécessaire dans ce cas :

Le fait que le test de divisibilité par 8 est perçu comme fondamentalement différent des autres, se retrouve par le fait que plusieurs élèves l’ont carrément oublié dans leur script, ou mis entre parenthèses (réminiscence d’une étape non vue par le prof ?) :

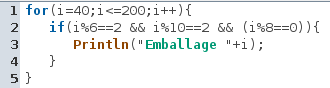
Le plus remarquable avec ce script est qu’il a été construit par un élève ayant 2 de moyenne en maths...

Il y a deux façons de traiter la multiplicité de tests : La version algorithmique (si un test réussit, on passe au suivant ; s’il réussit on passe au suivant) :

Et la version logique (construction d’un booléen géant par conjonction de booléens) :

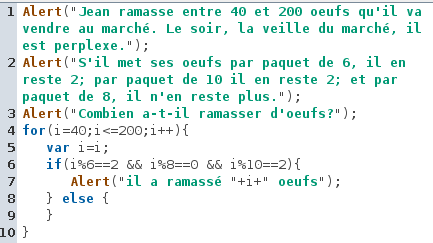
La plupart des élèves ont préféré faire des tests imbriqués plutôt qu’un test unique. Cela est visiblement dû à ce que les élèves savent que la conjonction est une opération binaire, mais ignorent qu’elle est aussi ternaire (parce qu’associative). Le « switch..case » qui permet d’abréger les tests imbriqués a été pratiqué lors du TP précédent mais aucun élève ne l’a utilisé ici.

La différence entre les deux méthodes se voit encore plus dans le deuxième exercice :

Version algorithmique :

Version logique :

Et avec un indice au nom plus parlant :