Types de base en Ocaml
Entre deux entiers comme 5 et 8 on peut réaliser plusieurs opérations mais elles ne donnent pas des résultats du même type :
# 5+8 ;;
- : int = 13Comme 5 et 8 sont des entiers, et qu’Ocaml a l’obligeance de nous signaler que leur somme 13 est un entier, on en déduit que l’addition est une opération binaire entre entiers (à un entier elle associe un entier).
L’addition, la soustraction, la multiplication, la division et l’exponentiation [1] sont des opérations binaires internes : à deux objets d’un type donné elles associent un objet de même type.
Il existe également des opérations binaires qui, à deux objets de type entier (par exemple) associent un booléen, et qu’on appelle relations (ou graphes...). Par exemple la relation d’ordre
# 5<8 ;;
- : bool = trueL’égalité, les relations d’ordre (strict ou large), la divisibilité sont des relations. Noter qu’il y a aussi des opérations booléennes internes (à deux booléens elles associent un booléen). Les plus connues sont la conjonction && et la disjonction ||. Il y a deux relations particulièrement importantes en mathématiques : l’égalité (c’est une relation d’équivalence) et l’appartenance (reliant un élément à une collection, par exemple un ensemble).
Ces exemples (ainsi que le pgcd, le produit scalaire, la distance etc) montrent que la plupart des opérations sont binaires : à deux objets mathématiques, elles associent un troisième objet.
Comment regrouper deux objets en un seul ?
En Ocaml, il y a un type permettant de créer un objet à partir de deux objets : le couple d’objets. Par exemple si on veut comparer ou additionner 5 et 8, on peut considérer qu’on a une fonction qui au couple (5,8) associe true (car 5 est plus petit que 8) ou 13 (qui est la somme de 5 et 8).
Comme les couples forment un produit cartésien, le type des couples est un type produit :
# (5,8) ;;
- : int * int = (5, 8)L’ensemble des couples d’entiers est le produit cartésien de l’ensemble des entiers par l’ensemble des entiers.
Il est donc logique de s’attendre à ce que le type de la relation d’ordre soit int * int -> bool et que le type de l’addition (des entiers) soit int * int -> int. Or ce n’est pas le cas :
# (<) ;;
- : 'a -> 'a -> bool = <fun>
# (+) ;;
- : int -> int -> int = <fun>Pour comprendre ces notations, on va utiliser plus bas la décurryfication. Ce changement de point de vue est dû à Moses Schönfinkel et a été répandu par Haskell Curry, d’où son nom.
Remarque : en Haskell c’est pareil :
Prelude> 5+8
13
Prelude> 5<8
True
Prelude> :t 13
13 :: Num a => a
Prelude> :t True
True :: Bool
Prelude> :t (5,8)
(5,8) :: (Num t, Num t1) => (t, t1)Avec une petite précision par rapport à Ocaml : Haskell rappelle que la relation d’ordre n’est définie sur un type a, que si ce type est doté d’un algorithme permettant de ranger les objets (et pareil, l’addition n’a de sens que sur les types numériques) :
Prelude> :t (<)
(<) :: Ord a => a -> a -> Bool
Prelude> :t (+)
(+) :: Num a => a -> a -> aTypes des fonctions
À partir des types bool et int on peut créer trois nouveaux types auxquels je propose de donner des noms (pour s’y repérer un peu : qui a réussi à se repérer sur une carte sans nom de lieu ?) :
- le type
bool -> boolest celui des fonctions qui, à un booléen, associent un booléen. Je propose d’appeler ce type celui des fonctions booléennes. La seule fonction utile ayant ce type est la négation logique :
– : bool -> bool =
- le type
int -> boolest celui des fonctions qui, à chaque entier, associent une valeurtrueoufalseselon que l’entier vérifie ou non une propriété. Je propose alors de l’appeler type des prédicats sur les entiers (ou propriétés des entiers). Je parlerai de prédicat (logique mathématique) pour les propriétés sur les entiers, et réserverai le terme de relation (mathématiques) lorsque le booléen est associé à deux objets. Les prédicats sur les entiers sont très nombreux (parité, primalité etc). Par exemple la parité en Ocaml :
# let pair entier = entier mod 2 = 0;;
val pair : int -> bool = <fun>
# pair 5 ;;
- : bool = false
# pair 8 ;;
- : bool = trueet en Haskell :
Prelude> let pair entier = mod entier 2 == 0
Prelude> pair 5
False
Prelude> pair 8
True
Prelude> :t pair
pair :: Integral a => a -> BoolUn prédicat sur les entiers est associé à un ensemble d’entiers (ceux qui vérifient la propriété). Un ensemble récursif en est un exemple important (celui des nombres pairs par exemple). Il y a beaucoup de prédicats sur les entiers, mais ils forment un ensemble de Cantor et donc chaque prédicat est quelque part sur cet ensemble. Par exemple les entiers pairs sont situés au point d’abscisse 3/4 sur l’ensemble triadique de Cantor (il est sur dans l’ensemble).
- Le type
bool -> intn’est pas assez utile pour qu’on l’évoque ici, on ne le verra pas dans cet article. - Le type
int -> intpar contre est très répandu. Ce sont les fonctions qui, à chaque entier n, associe un entier un dépendant de n. Je propose donc de l’appeler type des suites entières (ou suites d’entiers). Là encore, il y en a beaucoup, au point que l’OEIS leur est consacrée. Une des plus célèbres de ces fonctions est la suite de Collatz.
Voici le vocabulaire utilisé dans cet article :
| type | nom |
bool |
booléen (ou proposition logique) |
bool -> bool |
fonction booléenne |
int -> bool |
prédicat |
int |
entier naturel |
int -> int |
suite d’entiers |
Type des fonctionnelles
L’étape suivante est la construction de types comme
f -> g où parmi f et g, au moins un des deux n’est pas un type de base. Par exemple le type bool -> bool est habité par 4 fonctions booléennes :
- l’identité
- la négation
- la constante
false - la constante
true
L’énumération ci-dessus est une fonction qui, à une fonction booléenne, associe son numéro (entier). Elle est donc de type
(bool -> bool) -> int.
Le type (int -> int) -> bool est celui des propriétés de suites d’entiers. Par exemple la suite de Fibonacci a la propriété d’être croissante.
Le type (int -> int) -> int est celui d’une fonctionnelle (qui, à une suite d’entiers, associe un entier). Par exemple le plus petit élément d’une suite d’entiers est un entier (la conjecture de Collatz annonce que c’est 1 pour la suite de Collatz).
Le type (int -> int) -> (int -> int) est aussi celui d’une fonctionnelle (à une suite d’entiers on associe une suite d’entiers). La suite des sommes partielles en est un exemple (à une suite elle associe une série qui est elle aussi une suite).
C’est assez abstrait tout ça, même en cherchant des exemples et des mots. Mais ça ne s’arrête pas là. On peut définir des types comme celui qui, à une fonctionnelle comme celles vues ci-dessus, associe une fonctionnelle...
Voici un exemple de fonction au type impressionnant :
# let majority a b c =
match a with
| false -> b && c
| true -> b || c
;;
val majority : bool -> bool -> bool -> bool = <fun>
# majority true false true ;;
- : bool = trueCurryfication
La curryfication est un changement de point de vue. Elle permet de voir autrement certaines fonctions (ou fonctionnelles). Tout d’abord, on convient que les parenthèses non écrites sont autour de la partie droite du type. Par exemple parmi (a -> b) -> c et a -> (b -> c) on convient (avec Schönfinkel et Curry) que c’est le deuxième qui représente le type a -> b -> c. Comme toutes les conventions de notations, celle-ci devient naturelle avec de l’entraînement.
Voici un exemple de curryfication, concernant la relation d’ordre : au lieu de la voir comme une fonction qui, au couple (x,y) d’entiers, associe le booléen disant si x est plus petit que y, Curry la voit comme une fonction (d’arité 1) qui, à l’entier x, associe le prédicat « est plus grand que x » (ou, ce qui revient au même, l’ensemble des entiers plus grands que x). Comme un prédicat est de type int -> bool, le type de la version curryfiée de la relation d’ordre est donc int -> (int -> bool) dont on a vu ci-dessus qu’il peut se noter sans parenthèses int -> int -> bool.
Comme une relation est conceptuellement la même chose qu’un graphe orienté, la vision de sa matrice d’adjacence comme une liste de colonne (ce que fait la curryfication) revient à la représentation de ce graphe par listes d’adjacences.
On voit qu’on est parti d’une fonction qui associe quelque chose de simple (un booléen) à deux entiers (donc on est parti d’une opération d’arité 2), et on est arrivé à une fonction qui associe quelque chose de compliqué (un prédicat) à un seul entier (donc la fonction est d’arité 1) : la curryfication fait baisser l’arité au prix d’une abstraction plus élevée.
Il en est de même pour la curryfication de l’addition : on part d’une opération interne d’arité 2, qui à deux entiers x et y associe leur somme, et après curryfication on arrive à une fonction qui, à un entier x, associe une fonction affine (de coefficient directeur 1 et d’ordonnée à l’origine x). Elle est donc de type int -> (int -> int) soit int -> int -> int. Or une fonction qui, à un entier, associe une fonction, c’est une suite de fonctions. Là encore il y a un changement radical de point de vue sur cette opération binaire. Au lieu de voir l’addition des entiers comme une opération (d’arité 2) Curry la voit comme une collection de fonctions affines, dont les premières sont l’identité, la fonction sucesseur etc.
Tables de multiplication
De même, la multiplication est une opération binaire (d’arité 2) dont une table de valeurs est bidimensionnelle : la table de Pythagore. La curryfication fait passer d’un tableau de dimension 2 à une liste de fonctions linéaires (comme les bâtons de Neper). Ce point de vue se retrouve dans l’expression « la table de 4 » qui désigne l’une des colonnes de la table de Pythagore. Par exemple pour retrouver 6×4, il suffit de chercher le 6e terme de la suite des multiples de 4, et cela ne nécessite que de
- savoir compter jusqu’à 6,
- connaître la table de 4.
Et quand je dis « connaître la table de 4 » il peut s’agir d’un algorithme permettant de la reconstruire, par exemple en écrivant les chiffres 0,4,8,2,6 aussi souvent que nécessaire comme chiffres des unités et ne changer de chiffre des dizaines que lorsqu’on passe de 8 à 2 ou de 6 à 0. Bref, une connaissance procédurale de certaines colonnes de la table de Pythagore permet de retrouver celle-ci sans avoir à tout de suite apprendre les 100 valeurs qui sont inscrites dedans.
Cette idée (compter 6 fois de 4 en 4, plus généralement a fois de b en b) est d’ailleurs à la base de la définition récursive de la multiplication par Peano :
Version Ocaml
# let rec produit a b =
match a with
| 0 -> 0
| _ -> b + produit (a-1) b
;;
val produit : int -> int -> int = <fun>
# produit 6 4;;
- : int = 24Version Haskell
Prelude> let produit a b
| a==0 = 0
| otherwise = b+produit (a-1) b
Prelude> :t produit
produit :: (Eq a, Num a, Num a1) => a -> a1 -> a1
Prelude> produit 6 4
24Ocaml et Haskell n’infèrent pas le type de la multiplication de la même manière : pour Ocaml, a priori, les nombres à multiplier sont entiers (jusqu’à plus ample informé) et le produit aussi. Alors que pour Haskell, les deux facteurs doivent être des nombres (de types a et a1) et le produit est du même type que le second facteur, mais il faut aussi que le premier facteur puisse être comparé avec 0.
L’idée de voir la table de Pythagore comme une collection de fonctions se retrouve
- dans l’usage du pluriel « Les tables de multiplication »
- dans le mot « livret » utilisé dans certains pays francophones pour désigner ladite table de Pythagore.
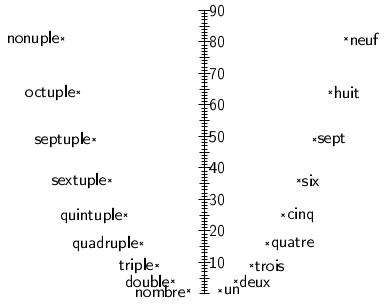
Chaque colonne de la table de Pythagore est en fait un tableau de valeur d’une fonction (identité, double, triple etc) et j’ai fabriqué un vrai livret où chaque page représente non pas un tableau, mais un diagramme sagittal :
Il peut être intéressant de tester l’utilisation de ce livret pour enseigner les tables de multiplication notamment à des élèves dys.
D’après l’Encyclopédie de d’Alembert et Diderot, la connaissance de la table de Pythagore était jugée indispensable au XVIIIe siècle :
il est absolument nécessaire que ceux qui apprennent l’Arithmétique, sachent par cœur les différentes multiplications contenues dans cette table
La nécessité de chercher l’intersection d’une ligne et d’une colonne était également connue des encyclopédistes :
Exemple. Supposé qu’il faille savoir le produit de 6 multipliés par 8, cherchez le chiffre 6 dans la premiere colonne horisontale, qui commence par 1 ; ensuite cherchez le chiffre 8, dans la premiere colonne perpendiculaire qui commence également par 1.
Le quarré ou la cellule de rencontre, c’est-à-dire où la colonne horisontale de 6 se rencontre avec la colonne perpendiculaire de 8, contient le produit qu’on cherche, savoir 48.
Comme je l’avais écrit plus haut, le fait de nommer un concept aide à réifier ce concept. Les fonctions qui forment les colonnes de la table de Pythagore possèdent des noms numéraux en l’occurence) :
En Ocaml
# let double x = 2*x;;
val double : int -> int = <fun>
# let triple x = 3*x;;
val triple : int -> int = <fun>
# let quadruple x = 4*x;;
val quadruple : int -> int = <fun>
# let quintuple x = 5*x;;
val quintuple : int -> int = <fun>
# let sextuple x = 6*x;;
val sextuple : int -> int = <fun>
# let septuple x = 7*x;;
val septuple : int -> int = <fun>
# let octuple x = 8*x;;
val octuple : int -> int = <fun>
# let nonuple x = 9*x;;
val nonuple : int -> int = <fun>
# sextuple 4;;
- : int = 24
# quadruple 6;;
- : int = 24En Haskell
Prelude> let double = (*) 2
Prelude> let triple = (*) 3
Prelude> let quadruple = (*) 4
Prelude> let quintuple = (*) 5
Prelude> let sextuple = (*) 6
Prelude> let septuple = (*) 7
Prelude> let octuple = (*) 8
Prelude> let nonuple = (*) 9
Prelude> let décuple = (*) 10
Prelude> quadruple 6
24
Prelude> sextuple 4
24L’idée de curryfier la multiplication ne date pas de Curry, puisque vers l’an 1000, Bernelin de Paris y fait allusion dans un manuscrit sur l’abaque de Gerbert. Voici un livret réumant sa vision de l’apprentissage verbal des tables de multiplication :
Et le source de ce livret :
infixe et préfixe
Les fonctions (d’arité 1) ne peuvent être données que sous deux formes :
- La notation préfixe où le nom de la fonction est donné comme sujet de la phrase, avant de nommer ce sur quoi porte la fonction. C’est la notation la plus courante, par exemple dans l’expression « la racine de 25 » c’est le premier mot (racine) qui désigne la fonction, et non 25 qui est l’argument de la fonction.
- La notation suffixe où, au contraire, on cite d’abord l’argument, et ensuite ce qu’on lui fait subir. Bien plus rare, on la ne la trouve guère que dans la factorielle.
On note que la notation polonaise inverse est suffixe, et que sur la plupart des calculatrices (RPN ou non) il est possible d’entrer de manière suffixe les fonctions opposé (avec le bouton +/-) et inverse (en général noté x-1).
Les opérations d’arité 2, peuvent être notées de 3 manières différentes :
- préfixe, comme par exemple le pgcd et le maximum (ce sont des opérations, dont l’arité peut d’ailleurs être plus grande que 2) que l’on cite avant leurs arguments,
- suffixe (mais pas dans la vie courante, uniquement en RPN),
- mais aussi infixe, où l’on place le nom de l’opération entre ses deux opérandes. C’est de loin la notation la plus courante pour les opérations classiques : addition, multiplication etc.
La curryfication s’applique à une opération notée préfixe. C’est peut-être ce qui explique les difficultés à concevoir la curryfication mais aussi certaines difficultés liées (c’est le cas de le dire) à la notation préfixe. Par exemple si un élève ne voit que le début de la phrase « le pgcd de 4 et 6 » il va croire que pgcd est une fonction et cherchera l’image de 4 par cette fonction [2]. Le c de pgcd veut dire « commun » ce qui devrait suffire à rappeler que l’opération pgcd est d’arité plus grande que 1, mais il n’est pas certain que les élèves se rappellent la signification de « plus grand commun diviseur ». Noter que la curryfication donne un sens à l’expression « le pgcd de 4 » : il s’agit de la fonction qui, à tout entier, associe son pgcd avec 4 :
- 1 si le nombre est impair,
- 4 si le nombre est divisible par 4,
- 2 si le nombre est pair mais pas divisible par 4.
Pour une opération notée infixe comme la multiplication, il y a deux manières d’envisager la curryfication. 6 * 4 par exemple peut être vu comme
-
(6 *) 4: la fonction sextuple, notée suffixe, appliquée de façon préfixe à 4 (soit le sextuple de 4) ; -
6 (* 4): la fonction quadruple, notée préfixe, appliquée de façon suffixe au nombre 6.
La notation infixe des opérations d’arité 2 favorise la vision curryfiée décrite plus haut à propos de la multiplication : au lieu de la version préfixe « le produit de 6 et 4 » pour laquelle on se met en mode multiplication avant même d’avoir entendu quels sont les deux nombres à multiplier entre eux, on entend d’abord 6 ce qui prépare à chercher la table de 6 (reste à savoir laquelle, ici c’est celle de multiplication) avant de connaître la nature de l’opération à effectuer et le second opérande.
La notation infixe aide à distinguer l’ordre dans lequel s’effectue une opération non commutative. Par exemple « a moins b » revient à « b ôté de a » et on sait que « a exposant b » (ou « a élevé à la puissance b ») n’est pas forcément la même chose que « b exposant a ». Au fait dans « a exposant b » il se trouve que b est l’exposant de a. Ne pas lire tous les mots d’une phrase peut aboutir à comprendre la phrase à l’envers...
La programmation objet est proche de la notation infixe. L’exemple de Python sera décrit plus en détail plus bas, mais déjà on peut voir que multiplier 6 par 4 revient à appliquer à 6 la « méthode » de multiplication par 4, qui est donc une fonction (les méthodes sont des fonctions) obtenue par curryfication :
>>> 6*4
24
>>> (6).__mul__(4)
24Les relations entre objets aussi, sont souvent notées infixes. Par exemple on dit que 4 est inférieur à 6, et pas que 4 et 6 vérifient la relation d’infériorité (cette dernière phrase étant suffixe). On dit souvent que 2+2 égale 4, moins souvent que 2+2 et 4 sont égaux (suffixe) ou qu’il y a égalité entre 2 et 4 (préfixe).
Arité variable au bac de NSI
Si une fonction f d’arité 2 vérifie
- l’associativité f(f(a,b),c) = f(a,f(b,c))
- l’existence d’un élément neutre e tel que f(e,a)=f(a,e)=a
alors on peut l’appliquer à une collection (une liste par exemple) de taille quelconque, avec la définition récursive :
- si la liste est vide on renvoie l’élément neutre e de f ;
- sinon
- on applique récursivement la fonction à la liste privée de son premier élément, pour obtenir un nombre B,
- on renvoie f(a,B).
Au bac de NSI il y a une épreuve pratique Python où on doit programmer ce genre de fonctions sur les listes, en particulier
- la taille de la liste (ici c’est la fonction successeur d’arité 1 qui est utilisée)
- le maximum de la liste (ici c’est la fonction qui à deux entiers associe le plus grand d’entre eux, l’élément neutre étant -∞),
- le minimum de la liste (ici c’est la fonction d’arité 2 qui à deux entiers associe le plus petit d’entre eux, l’élément neutre étant +∞),
- la somme des éléments d’une liste de nombres (ici c’est l’addition, l’élément neutre étant 0)
Mais il y a aussi le produit des éléments d’une liste (par exemple la factorielle), le pgcd d’une liste d’entiers, le ppcm d’une liste d’entiers, et même les fonctions all et any de Python (conjonction et disjonction appliquées à une liste de booléens).
En Haskell, la fonction foldl permet de programmer cette conversion de l’arité 2 vers une arité variable. On remarque que si la liste ne contient qu’un seul élément, on obtient cet élément, ce que les élèves trouvent en général assez logique (et cela permet notamment de donner une note de contrôle continu même si la moyenne trimestrielle n’est calculée qu’à partir d’une seule note).
Affectation
Une opération particulièrement complexe en infiormatique est l’affectation d’une variable. Une variable est constituée d’un nom et d’une valeur, selon les encyclopédistes :
VARIABLE, adj. (Alg. & Géom.) on appelle quantités variables en Géométrie, les quantités qui varient suivant une loi quelconque. Telles sont les abscisses & les ordonnées des courbes, leurs rayons osculateurs, &c.
On les appelle ainsi par opposition aux quantités constantes, qui sont celles qui ne changent point, comme le diametre d’un cercle, le parametre d’une parabole, &c.
On exprime communément les variables par les dernieres lettres de l’alphabet x, y, z.
(on remarque que pour d’Alembert, le mot « variable » est un adjectif, le nom « variable » n’étant d’ailleurs qu’un raccourci pour « quantité variable »)
L’idée de représenter une variable comme l’association d’une valeur à un nom (c’est-à-dire une fonction) ne se voit pas dans la définition d’une variable mais dans celle d’une référence (qui est l’équivalent d’une variable en Ocaml) :
REFERER, v. act. (Gram.) c’est renvoyer une chose à une autre. Je m’en refere à monsieur un tel ; c’est aussi rendre compte
Noter que la notion de fonction, chez les encyclopédistes, est moins générale qu’aujourd’hui :
FONCTION, s. f. (Algebre.) ... on appelle fonction de x, ou en général d’une quantité quelconque, une quantité algébrique composée de tant de termes qu’on voudra, & dans laquelle x se trouve d’une maniere quelconque, mêlée, ou non, avec des constantes
Affecter une variable, c’est modifier sa valeur. En Ocaml par exemple la fonction affecter peut se définir par injection d’une valeur n dans une référence x :
# let affecter x n = x:=n;;
val affecter : 'a ref -> 'a -> unit = <fun>
# let x = ref 3;;
val x : int ref = {contents = 3}
# affecter x 5;;
- : unit = ()
# x;;
- : int ref = {contents = 5}On voit qu’après l’affectation, x ne se refère plus à 3 mais à 5.
Il y a alors changement d’état de l’ordinateur. Toujours selon les encyclopédistes :
ETAT, s. m. (Métaph.) Etat d’un être en général & dans le sens onthologique, c’est la co-existence des modifications variables & successives, avec les qualités fixes & constantes : celles-ci durent autant que le sujet qu’elles constituent, & elles ne sauroient souffrir de détriment sans la destruction de ce sujet. Mais les modes peuvent varier, & varient effectivement ; ce qui produit les divers états, par lesquels tous les êtres finis passent.
En Haskell, l’état de la machine est modélisé par une monade (informatique) qui s’appelle justement State.
L’affectation curryfiée est quelque chose de complexe : une fois choisie une variable (ou ici, une référence) x, on se retrouve avec une fonction qui, à un entier, associe du rien (unit) et met cet entier dans x. Cette fonction est abstraite et résume en elle seule toutes les affectations que l’on peut faire sur x. Inverser les rôles du nom et de la valeur ne modifie pas radicalement la complexité :
# let injecter n x = x:=n;;
val injecter : 'a -> 'a ref -> unit = <fun>
# injecter 2 x;;
- : unit = ()
# x;;
- : int ref = {contents = 2}Ici, une fois choisi un entier, on se retrouve avec une fonction modélisant les affectations possibles par cet entier. L’affectation, qui est d’arité 2 puisqu’elle concerne un nom et une valeur, est en général notée infixe. Dans le premier cas on écrit x←n, x :=n ou x prend_la_valeur n (en Python c’est carrément x=n). Dans le second c’est n→x ou n sto→ x. Mais la notation préfixe est finalement plus naturelle pour une affectation : « mettre n dans x », « stocker n dans x », « injecter n dans x » ou « reférer x à n » sont relativement simples à concevoir, il est donc surprenant que la notation infixe pour l’affectation soit si répandue dans des langages de programmation qui ont la prétention d’être proches de la langue naturelle...
Sofus
La fonction successeur est ... une fonction : à un entier elle fait correspondre un autre entier, elle ne fait que décrire la relation entre ces deux entiers. Souvent en programmation on a besoin d’affecter une variable par le successeur de sa valeur actuelle (incrémenter la variable). On peut faire cela en Ocaml avec les références :
# let incrementer x = x:=!x+1;;
val incrementer : int ref -> unit = <fun>
# let decrementer x = x:=!x-1;;
val decrementer : int ref -> unit = <fun>
# x;;
- : int ref = {contents = 2}
# incrementer x;;
- : unit = ()
# x;;
- : int ref = {contents = 3}On peut alors écrire un interpréteur Sofus en Ocaml :
# let doubler x = x:=!x*2;;
val doubler : int ref -> unit = <fun>
# let tripler x = x:=!x*3;;
val tripler : int ref -> unit = <fun>
# let quadrupler x = x:=!x*4;;
val quadrupler : int ref -> unit = <fun>
# let quintupler x = x:=!x*5;;
val quintupler : int ref -> unit = <fun>
# let sextupler x = x:=!x*6;;
val sextupler : int ref -> unit = <fun>
# let septupler x = x:=!x*7;;
val septupler : int ref -> unit = <fun>
# let octupler x = x:=!x*8;;
val octupler : int ref -> unit = <fun>
# let nonupler x = x:=!x*9;;
val nonupler : int ref -> unit = <fun>
# let decupler x = x:=!x*10;;
val decupler : int ref -> unit = <fun>
# x;;
- : int ref = {contents = 3}
# tripler x;;
- : unit = ()
# x;;
- : int ref = {contents = 9}Par exemple ce fichier permet de programmer en Sofus dans Ocaml [3] :
let de = "de"
let par = "par"
let dans = "dans"
let mettre d dans x = x:=d
let incrementer x = x:=!x+1
let decrementer x = x:=!x-1
let augmenter x de d = x:=!x+d
let diminuer x de d = x:=!x-d
let multiplier x par d = x:=!x*d
let diviser x par d = x:=!x/d
let doubler x = x:=!x*2
let tripler x = x:=!x*3
let quadrupler x = x:=!x*4
let quintupler x = x:=!x*5
let sextupler x = x:=!x*6
let septupler x = x:=!x*7
let octupler x = x:=!x*8
let nonupler x = x:=!x*9
let decupler x = x:=!x*10Quel est le type d’une affectation ( « mettre dans » ) ? On a vu plus haut que sa version curryfiée est 'a ref -> 'a -> unit : 'a étant le type de ce qui est dans la variable (appelé « type de la variable » pour faire plus court), on a une fonction qui, à une variable (de type 'a ref c’est-à-dire une référence -notée suffixe- vers un 'a), associe une fonction de type 'a -> unit c’est-à-dire une fonction qui à ce qu’on met dans la variable, associe du rien. Le quadruplement est de type plus simple puisqu’il donne un int ref -> unit :
# let dans = "dans";;
val dans : string = "dans"
# let mettre d dans x = x:=d;;
val mettre : 'a -> 'b -> 'a ref -> unit = <fun>
# let quadruple x = 4*x;;
val quadruple : int -> int = <fun>
# let quadrupler x = mettre (quadruple !x) dans x;;
val quadrupler : int ref -> unit = <fun>On voit au passage la différence, déjà évoquée, entre quadruple et quadrupler : le premier est un nom donc désigne une fonction (c’est-à-dire une relation), le second est un verbe donc désigne une action. Le lien entre les deux se voit dans la définition donnée ci-dessus du quadruplement : quadrupler une variable, c’est remplacer sa valeur actuelle par le quadruple de celle-ci.
Décurryfication
Inverse de la curryfication, la décurryfication augmente l’arité d’une fonction pour en faire une opération plus rapide à décrire pour un humain. Elle est donc intéressante pour donner un nom à une fonction de type un peu complexe.
Par exemple en voyant le type
bool -> bool -> bool (fonction qui, à un booléen, associe une fonction booléenne) comme
(bool,bool) -> bool on se rend compte qu’il s’agit juste d’une opération booléenne.
En voyant le type
int -> int -> bool (suite de prédicats sur les entiers) comme la version décurryfiée
(int,int) -> bool on se rend compte qu’il s’agit juste d’une relation entre entiers.
En voyant le type
int -> int -> int (suite de suites d’entiers) comme la version décurryfiée
(int,int) -> int on se rend compte qu’il s’agit d’une opération (d’arité 2) sur les entiers.
La décurryfication peut se faire mentalement avec de l’entraînement (et cet entraînement est même ludique). L’idée est de ne garder que la dernière flèche (celle qui est à droite) et mettre tout le reste dans un tuple.
Par exemple l’affectation qui, on l’a vu, est de type
'a ref -> 'a -> unit, se décurryfie en
('a ref, 'a) -> unit donc une opération qui s’applique à une référence sur un 'a (la variable) et un 'a (ce qu’on va mettre dans la variable) et ne renvoie rien puisqu’on veut juste qu’elle produise un effet.
Même en logique, la décurryfication est utile, elle consiste essentiellement à voir une chaîne d’implications comme « si a alors, si b alors c » en une seule implication comme « si a et b alors c ».
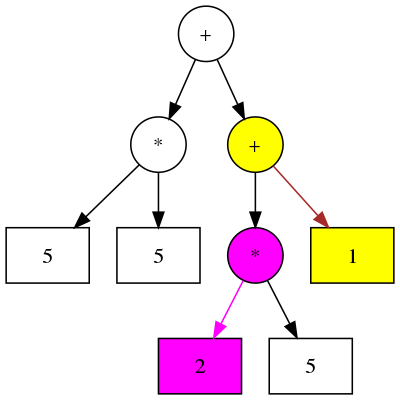
La figure 4 de Shannon
Dans an investigation on the laws of thought, George Boole écrivait ceci :
Suppose, then, such knowledge is to the following effect, viz., that the members of that portion which possess the property x, possess also a certain property u, and that these conditions united are a sufficient definition of them. We may then represent that portion of the original class by the expression ux (II. 6). If, further, we obtain information that the members of the original class which do not possess the property x, are subject to a condition v, and are thus defined, it is clear, that those members will be represented by the expression v (1 − x). Hence the class in its totality will be represented by
ux + v (1 − x).
Pour une fonction booléenne f d’arité 1, Boole donne le développement suivant :
f (x) = f (1) x + f (0) (1 − x)
On peut montrer cette formule par une table de vérité, comme l’écrit Boole :
x regarded as a quantitative symbol admits only of the values 0 and 1, and for
each of these values the development f (1) x + f (0) (1 − x), assumes the same value as the function f (x).
Ensuite, Boole généralise à des opérations (d’arité 2 dans un premier temps) booléennes, avec ce développement :
f (x, y) = f (1, y) x + f (0, y) (1 − x) ;
puis à trois variables booléennes :
f (x, y, z) = f (1, 1, 1) xyz + f (1, 1, 0) xy (1 − z) + f (1, 0, 1) x (1 − y) z
+ f (1, 0, 0) x (1 − y) (1 − z) + f (0, 1, 1) (1 − x) yz
+ f (0, 1, 0) (1 − x) y (1 − z) + f (0, 0, 1) (1 − x) (1 − y) z
+ f (0, 0, 0) (1 − x) (1 − y) (1 − z)
En 1938, Shannon trouve le moyen de représenter par un circuit électronique ce résultat de Boole, appelé aujourd’hui algorithme de Quine-McCluskey.
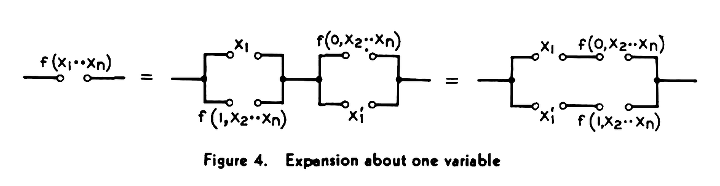
En fait il s’agit de curryfication des opérateurs booléens...
La programmation objet et l’arité 2
Les langages de programmation objet permettent de définir des opérations d’arité 2, et ensuite de les utiliser de manière infixe. Cela permet d’utiliser ces langages pour verbaliser le cours de mathématiques comme le préconisait Seymour Papert, en laissant l’enfant apprendre par les explications qu’il donne à une machine. Dans cette partie finale (un peu hors sujet) on va comparer les façons de faire avec plusieurs de ces langages. Avec l’exemple de l’addition des vecteurs.
Python
Pour créer un vecteur, il suffit de définir une classe et une méthode de création du vecteur :
class Vecteur:
def __init__(self,x,y):
self.x=x
self.y=yPour créer des vecteurs, il n’y a même pas besoin de citer nommément cette méthode :
u = Vecteur(3,2)
v = Vecteur(8,5)Mais en essayant d’afficher le vecteur u + v on a un message d’erreur :
TypeError: unsupported operand type(s) for +: 'Vecteur' and 'Vecteur'disant que Python ne sait pas additionner un vecteur avec un vecteur. Normal, on ne le lui a jamais appris. Ceci est vite corrigé dans la définition de la classe Vecteur mais à condition de savoir qu’en Python, la méthode utilisée par un « + » infixe s’appelle __add__ :
def __add__(self,v):
return Vecteur(self.x+v.x,self.y+v.y)Après ça, l’écriture u+v désigne bien la somme des deux vecteurs. Pour en savoir plus, voir ici.
La programmation objet de Python permet de définir une méthode qui sera appelée par un « + » infixe, c’est-à-dire de définir sa propre addition et de l’appeler simplement en écrivant le signe « + » entre deux opérandes. Il en est de même pour Ruby :
Ruby
En Ruby, pour définir ce qu’est un vecteur, il suffit d’expliquer comment on en crée un (avec deux nombres qui sont ses coordonnées) :
class Vecteur
def initialize(x,y)
@x,@y = x,y
end
endLe symbole arobase est une abréviation pour « mon mien à moi » ce qui fait que @x veut dire « mon abscisse » (du point de vue du vecteur).
Pour créer des vecteurs u(3,2) et v(8,5) on fait
u = Vecteur.new(3,2)
v = Vecteur.new(8,5)Mais
u+v
ne donne pas la somme des deux vecteurs, mais un message d’erreur précisant que les vecteurs n’ont pas de méthode appelée « + ». Pour pouvoir effectivement additionner deux vecteurs, on doit donc, dans la définition de la classe Vecteur, expliquer ce qu’on entend par « + » :
def + (u)
Vecteur.new(@x+u.x,@y+u.y)
endLa méthode d’addition est une fonction appartenant au vecteur, ayant pour argument un autre vecteur, et renvoyant un nouveau vecteur (la somme) ayant pour coordonnées les sommes des coordonnées des deux vecteurs. Comme en programmation objet il est d’usage de citer l’objet, puis sa méthode et enfin l’argument de la méthode, la notation est de facto infixe : on écrit juste u + v pour créer le vecteur somme. Pour en savoir plus, voir ici.
Les langages de programmation objet comme Python et Ruby permettent donc de construire un savoir algébrique en permettant aux élèves d’inventer leurs propres opérations et de calculer avec ces opérations. On peut voir aussi
- l’exemple des fractions en Python
- celui des extensions quadratiques
- celui des quaternions en Python et en Ruby
Le calcul matriciel (en particulier avec des matrices de RegEx) et les fractions de Farey sont des exemples restant à explorer.

Commentaires