Modélisation de la propagation des feux de forêt

On utilise les automates cellulaires. La forêt est représentée par des « cellules » :
- les vertes : arbres,
- les blanches : rien,
puis, on allume une cellule (cellule rouge)...

- Si un arbre (cellule verte) est à « proximité directe » (au-dessus, au-dessous, à gauche ou à droite) d’un arbre en flamme (cellule rouge), à l’instant suivant, il sera en flamme.
- Si un arbre est en flamme, à l’instant suivant, il devient cendres (cellule grise).
- Si un arbre est en cendres, à l’instant suivant, il n’y a plus rien à brûler (cellule blanche).
Feuille de route :
- Comprendre et formaliser le modèle avec des automates cellulaires.
- Éventuellement réaliser une simulation.
- Influence de la proportion d’arbres dans la propagation du feu : notion du seuil de percolation...
- Un modèle mathématique peut toujours être amélioré : comment tenir compte d’autres facteurs dans le modèle ? Ex : vent, différents types de végétation, de terrain, etc.
- Que ce passe-t-il si on met d’autres règles de « transition » ? Si on travaille uniquement sur une ligne de cellules ? Si on a d’autres liens de voisinage entre les cellules ? Etc.
Bonus : question/devinette
Quel est le point commun entre :
- la propagation d’un feu de forêt,
- la propagation d’un virus informatique,
- l’évolution d’un embouteillage sur la route du littoral,
- un café expresso qui coule dans un percolateur...?
Mouvements de foule
(suite à la conférence de Juliette Venel lors du congrès 2010)
Situation : on prend une salle de cours (rectangle) avec deux issues de secours. On cherche à connaître le temps moyen d’évacuation des n élèves.
Diverses modélisations pourront être abordées : de manière discrète ou continue, avec des petites valeurs de n, avec ou sans obstacles. On pourra aussi réaliser des simulations.
Crypter et décrypter des textes : du code César... à la machine Enigma

Cryptanalyse du code :
Un outil : analyse des fréquences d’Al-Kindi. Cela marche d’autant mieux si le texte est long.
Langue française (en %) :
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| 9.42 | 1.02 | 2.64 | 3.39 | 15.87 | 0.95 | 1.04 | 0.77 | 8.41 | 0.89 | 0.01 | 5.34 | 3.24 |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 7.15 | 5.14 | 2.86 | 1.06 | 6.46 | 7.90 | 7.26 | 6.24 | 2.15 | 0.01 | 0.30 | 0.24 | 0.32 |
Feuille de route :
- Qu’est ce que César a écrit à Cléopâtre ?
- Quel est le principe et la principale « vulnérabilité » du code César ?
- Éventuellement programmer un « logiciel » de cryptage/décryptage de texte avec le code César.
- Les raffinements du code César :
- Le code de Vigenère (Moyen-Âge) : quel est son principe ? Comment a-t-il été « craqué » ?
- La machine Enigma (Seconde Guerre mondiale) : quel est son principe ?

Les mathématiques du billard : comprendre les déplacements et les trajectoires possibles d’une boule de billard

Quelle trajectoire une boule peut-elle suivre ?
Pour la modélisation, on considèrera un billard spécial sur lequel :
- une boule est toujours lancée sans effet,
- une boule peut continuer indéfiniment sa course.
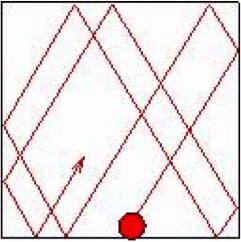
Feuille de route :
- Expliciter les règles de déplacement d’une boule sur ce billard.
- Une boule peut-elle faire une boucle ?
- Une boule peut-elle décrire une trajectoire qui ne repasse pas indéfiniment par les même points ?
- Une boule peut-elle être lancée de manière à ce qu’elle passe par tous les endroits du billard ? Ou au contraire, qu’elle évite une zone complète ?
- Et si on jouait sur un billard triangulaire ? Hexagonal ? Que se passerait-il ?

Commentaires