Parenthèses
Les expressions correctement parenthésées forment un langage algébrique, qui peut être reconnu par un automate à pile. Le cas de html est traité dans l’exercice 1 du sujet de NSI (jour 1) de métropole, dont voici un corrigé en ligne :
Notation polonaise
Le calcul sur une pile est ce qu’on obtient après compilation (voir plus bas). Le calcul lui-même est traité dans le premier exercice du sujet Liban-Mayotte 2022 (jour 2), dont voici un corrigé en ligne :
Dans toute la suite de cet article, on va étudier le sujet de l’agrégation d’informatique portant sur la compilation : comment, à partir d’une expression parenthésée (ou décrite par son arbre syntaxique qui est un arbre binaire), obtenir un programme similaire à ceux décrits ci-dessus ?
Compilation
1. Compilation d’expressions vers une machine à pile
1
On se propose de créer des utilitaires en Python (qui n’est pas le langage du sujet) pour lui déléguer la tâche de répondre à certaines des questions.
X = 2
Y = 5
VAR('X');CONST(1);ADD();VAR('Y');MUL()
print(pile)1.1
Une machine à pile
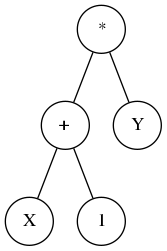
Question 1
Voici une machine à pile :
avec
pile = []
l’exécution du code donne 15.
Question 2 : la fonction exec
Avec
print(executer('VAR(X);CONST(1);ADD();VAR(Y);MUL()',{'X':2,'Y':5}))on retrouve les 15 de la question précédente.
Question 3 : la consommation en espace
Avec
print(conso_espace('VAR(X);CONST(1);ADD();VAR(Y);MUL()'))on obtient 2 : la pile culmine à une hauteur de 2.
1.2
Compilation simple des expressions arithmétiques
L’expression à compiler est donnée sous la forme d’un arbre binaire. Il est donc nécessaire de créer une classe BTree qui implémente les arbres binaires.
Avec
e = BTree('*',BTree('+',BTree('X'),BTree('1')),BTree('Y'))la variable e contient l’arbre de la question 1.
Dessiner les arbres
Voici une fonction Python qui, à partir d’un arbre décrit selon la syntaxe ci-dessus, produit un dessin de l’arbre :
def dessiner(arbre):
global da, cptr
if arbre is not None:
cptr += 1
num = str(cptr)
da.node(num,arbre.L,shape='circle')
if arbre.G is not None:
ng = dessiner(arbre.G)
da.edge(num,ng)
if arbre.D is not None:
nd = dessiner(arbre.D)
da.edge(num,nd)
return numElle utilise la variable globale da qui est définie au début :
from graphviz import *
da = Graph(format='png')
cptr = 0Avec
dessiner(e)
da.render()on obtient le dessin qui ouvre cette partie :
Le code produit par cet arbre est obtenu à l’aide du compilateur ci-dessous.
Question 4
Avec l’expression e ci-dessus,
compiler(e)
donne le programme de la question 1.
Question 6
Pour l’opposé on fait
C(e);OPP
Pour la soustraction on fait
C(e1);C(e2);OPP;ADD
1.3
Consommation en espace du code compilé
Question 7
La famille Gn
Elle est définie récursivement par
def G(n):
if n==0:
return BTree('0')
else:
return BTree('+',G(n-1),BTree(str(n)))En voici quelques représentants :
G0 :
G1 :
G2 :
G3 :
et G5 :
La famille Dn
Elle est définie récursivement par
def D(n):
if n==0:
return BTree('0')
else:
return BTree('+',BTree(str(n)),D(n-1))En voici quelques représentants :
D0 :
D1 :
D2 :
D3 :
et D5 :
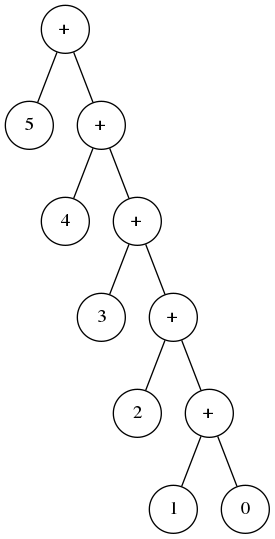
La consommation en espace de Dn (2) étant nettement moins grande que celle de Dn (n+1), cela motive l’onglet suivant.
Question 8
Pour une constante ou une variable, la consommation en espace est 1.
Pour une somme ou un produit, la consommation en espace est
T(e1)+T(e2)+1
1.4
Compilation qui minimise la consommation en espace
Questions 9 et 17
Avec
e = BTree('*',BTree('+',BTree('X'),BTree('1')),BTree('Y'))
print(S(e))on trouve 2.
Question 10
On trouve 2 pour les graphes Gn et Dn, sauf pour G0 et D0 qui ont un nombre de Strahler égal à 1.
Questions 11 et 18
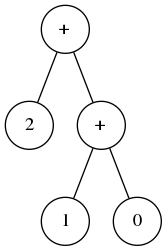
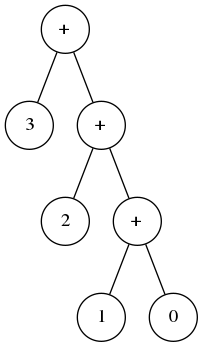
La compilation de G5 donne
CONST(0); CONST(1); ADD; CONST(2); ADD; CONST(3); ADD; CONST(4); ADD; CONST(5); ADDet la compilation de D5 donne
CONST(1); CONST(0); ADD; CONST(2); ADD; CONST(3); ADD; CONST(4); ADD; CONST(5); ADDQuestion 13
Un indice : Récurrence sur l’expression e
Question 14
Une expression ayant au maximum 7 nœuds internes a nécessairement au maximum 8 feuilles, et est donc de taille maximale 7+8==15. D’après le résultat de la question précédente, son nombre de Strahler est majoré par 4 cqfd.
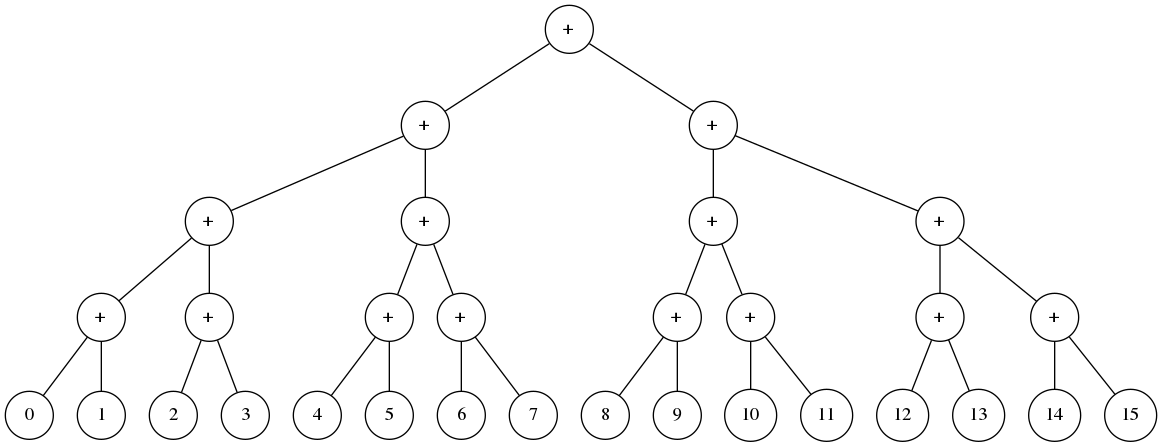
Question 15
Cette expression convient :
En effet elle se compile en
CONST(0); CONST(1); ADD; CONST(2); CONST(3); ADD; ADD; CONST(4); CONST(5); ADD; CONST(6); CONST(7); ADD; ADD; ADD; CONST(8); CONST(9); ADD; CONST(10); CONST(11); ADD; ADD; CONST(12); CONST(13); ADD; CONST(14); CONST(15); ADD; ADD; ADD; ADDqui fait culminer la hauteur de la pile à 5.
Question 16
Le nombre de Straheler de l’opposé d’une expression est 1 de plus que le nombre de Strahler de l’expression. Le code produit est encore
E(e)+';OPP'
Le nombre de Strahler d’une différence se calcule comme celui d’une somme. Le code produit dépend des nombres de Strahler des deux termes :
- si le nombre de Strahler de e1 est au moins aussi grand que celui de e2 alors la compilation donne
E(e1)+';'+E(e2)+'OPP; ADD'
- sinon la compilation donne
E(e2)+'; OPP; '+E(e1)+'; ADD'
Questions 19 et 20
La compilation passe par un parcours suffixe de l’expression. Ce parcours est de complexité linéaire par rapport à la taille de l’arbre. Mais à chaque étape on calcule récursivement le sous-arbre considéré, pour calculer le nombre de Strahler. L’algorithme est donc de complexité quadratique. Pour l’améliorer il faudrait calculer en même temps le nombre de Strahler et l’expression compilée.
2. Compilation d’expressions vers une machine à registres
2.1
Une machine à registres
On a vu que l’algorithme d’Ershov produit un code peu gourmand en espace. Dans cette partie on reprogramme l’algorithme d’Ershov pour une pile de longueur finie, simulée par une machine à registres.
2.2
Question 21
En soumettant au compilateur ci-dessus l’arbre de la première question :
on obtient
LOAD(R1,X)
MOV(R2,1)
ADD(R1,R1,R2)
LOAD(R2,Y)
MUL(R1,R1,R2)Question 22
Une fois exécuté le code compilé, le registre Rd contient le résultat du calcul, et les registres de numéros inférieurs à d contiennent les étapes intermédiaires du calcul.
Question 23
En compilant l’arbre D5
on obtient le programme
MOV(R1,5)
MOV(R2,4)
MOV(R3,3)
MOV(R4,2)
MOV(R5,1)
MOV(R6,0)
ADD(R5,R5,R6)
ADD(R4,R4,R5)
ADD(R3,R3,R4)
ADD(R2,R2,R3)
ADD(R1,R1,R2)qui utilise 6 registres et ne peut donc s’exécuter sur une machine à 5 registres. Plus généralement, il faut n+1 registres pour calculer Dn et l’expression Dn convient pour répondre à la question.
Question 24
L’arbre D5 se compile alors en
MOV(R1,1)
MOV(R2,0)
ADD(R1,R1,R2)
MOV(R2,2)
ADD(R1,R1,R2)
MOV(R2,3)
ADD(R1,R1,R2)
MOV(R2,4)
ADD(R1,R1,R2)
MOV(R2,5)
ADD(R1,R1,R2)qui n’utilise que deux registres.
3. Compilation d’expressions avec partage
3
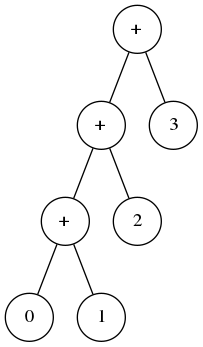
Dans cette partie, on abandonne les arbres syntaxiques comme
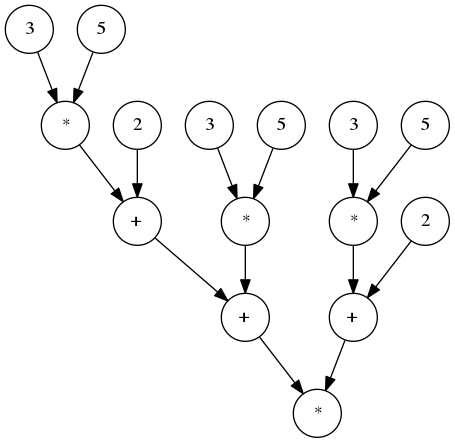
Pour leur préférer la version DAG (graphes orientés sans cycle) :
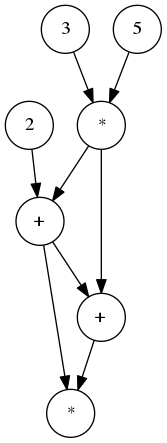
3.1
Introduction du problème
Question 29
L’arbre précédent
se compile par l’algorithme d’Ershov en
MOV(R1,3)
MOV(R2,5)
MUL(R1,R1,R2)
MOV(R2,2)
ADD(R1,R1,R2)
MOV(R2,3)
MOV(R3,5)
MUL(R2,R2,R3)
ADD(R1,R1,R2)
MOV(R2,3)
MOV(R3,5)
MUL(R2,R2,R3)
MOV(R3,2)
ADD(R2,R2,R3)
MUL(R1,R1,R2)qui utilise 3 registres, alors que le graphe correspondant
peut être évalué par
MOV(R1,3)
MOV(R2,5)
MUL(R1,R1,R2)
MOV(R2,2)
ADD(R1,R1,R2)
MUL(R2,R1,R2)qui n’utilise que deux registres.
Pour la suite, on considère le graphe
h0 = [[3],[3],[4],[5,4],[5,6],[6],[]]
dont le dessin est
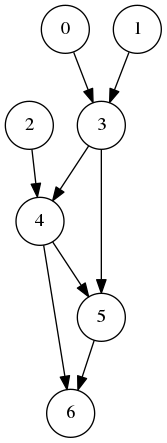
Question 30
Avec ça,
transpose(h0)
donne le graphe
Question 31
est_ordre(h0,[2,1,0,3,4,5,6])
s’évalue à True : il s’agit bien d’un ordre topologique.
ordre topologique
Avec l’ordre (2,1,0,3,4,5,6) le film de la compilation montre qu’à un moment on va avoir besoin de 4 registres simultanément (0,1,2 et 3) :
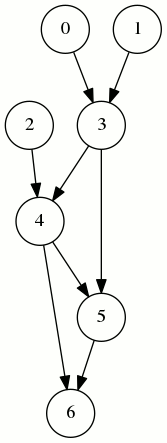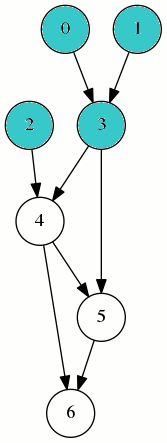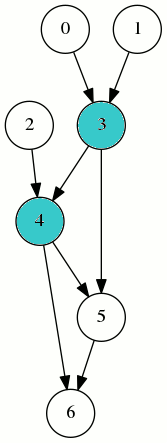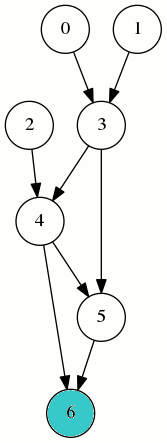
L’ordre (0,1,3,2,4,5,6) est un ordre topologique comme le montre
print(est_ordre(h0,[0,1,3,2,4,5,6]))
et donne une compilation ne nécessitant jamais plus de 3 registres :
Strahler
On redéfinit la notion de source à partir du nombre de prédécesseurs :
def nb_pred(sommet,graphe):
return len(transpose(graphe)[sommet])
def source(sommet,graphe):
return nb_pred(sommet,graphe)==0Question 33
Question 34
Question 35
On s’intéresse au graphe suivant :
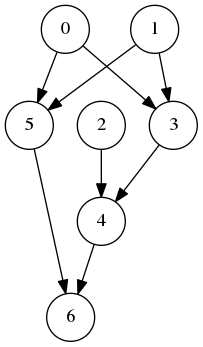
Son ordre de Strahler est
[0, 1, 3, 2, 4, 5, 6]
Mais sur ce graphe, la compilation selon cet ordre nécessite jusqu’à 5 registres :
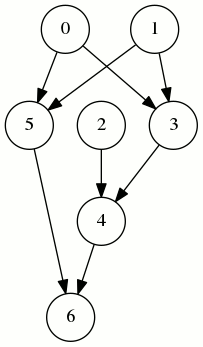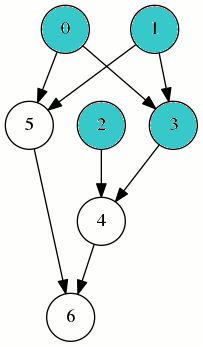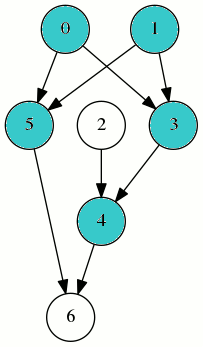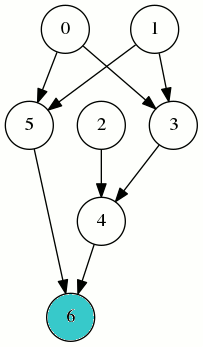
On peut faire mieux avec cet autre odre, dont on vérifie qu’il est bien un ordre topologique :
[0,1,3,5,2,4,6]
Il ne nécessite que 4 registres :
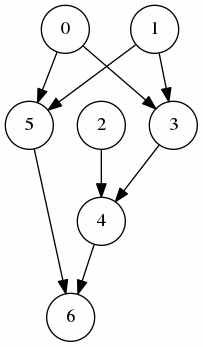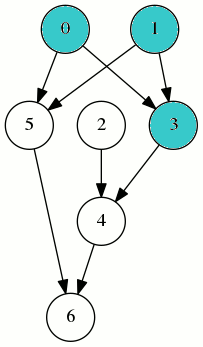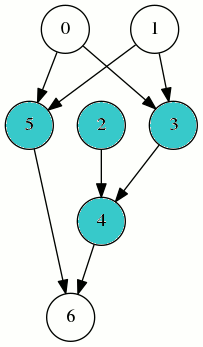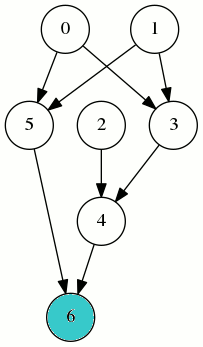
Dans le jeu du marquage, on autorise les mouvements de jetons et dans ce jeu sur le graphe ci-dessus, on arrive en un temps 8 à placer un jeton sur le sommet 6, en utilisant au maximum 3 jetons (mouvements 2,2,2,3,1,2,3,3) :
Jeu du marquage
Règle du jeu
Le jeu se joue sur un graphe orienté. Trois sortes de mouvements sont possibles :
- enlever un jeton d’un sommet,
- ajouter un jeton sur un sommet n’ayant aucun prédécesseur non couvert de jeton,
- si tous les prédécesseurs d’un sommet sont couverts de jetons, glisser l’un d’entre eux sur ce sommet.
Le but du jeu est de couvrir le puits par un jeton. Une stratégie est une suite de chiffres pris parmi 1, 2 et 3 qui amène à couvrir le puits par un jeton.
Question 36
La stratégie 2,2,3,1,2,3,3,3 permet de couvrir le sommet 6 par un jeton :
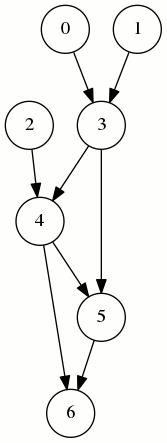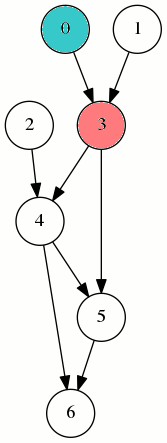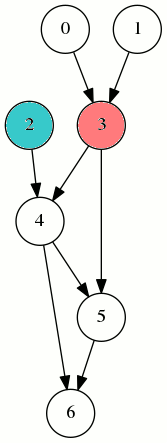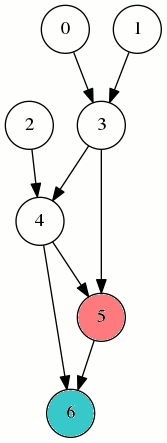
Elle n’utilise que 2 jetons en temps 8. Donc pour ce graphe, Mmin est égal à 2.
Question 37
La stratégie consistant à n’utliser que le mouvement 2 (en suivant par exemple un ordre topologique comme ceux vus précédemment) permet de couvrir le puits par un jeton, en plaçant n jetons (donc en temps n).
Question 38
Voici les premiers graphes pyramidaux :
P1 :
P2 :
P3 :
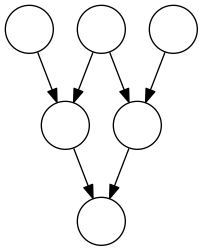
P4 :
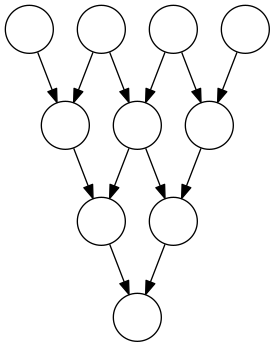
P5 :
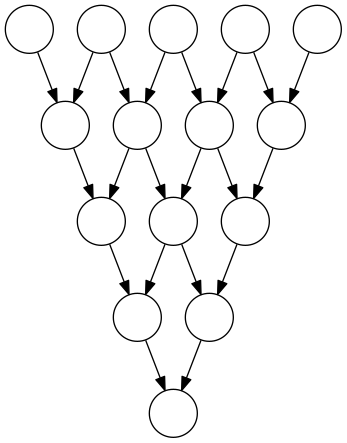
Une stratégie pour un graphe pyramidal (ci-dessous, P4) consiste à placer n jetons sur les n sources puis faire glisser les n-1 premiers d’entre eux vers les sources de Pn-1 etc :
Elle prend un temps n×(n-1)/2.
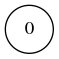
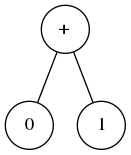
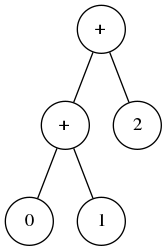
Commentaires