Anciens ateliers
Les anciens ateliers conservent, voire accroissent, leur succès :
Tangrams
Les tangrams attirent le regard, non seulement des visiteurs, mais même des autres exposants (métiers du bois) :

Ranger les pièces une fois qu’on a fini de jouer, n’est pas si aisé. Une élève de CM1 est fière d’y arriver en 7 secondes :

Bridge
Le bridge a fait son retour au Tampon :


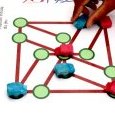
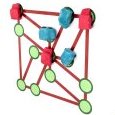
Polydrons
Au Moufia, on a pu bénéficier des polydrons, dont le succès ne décroit pas. Les enfants manipulent beaucoup et de façon autonome.





Au Tampon, privés de cette activité, les enfants se sont repliés sur ce qui était à leur portée :

Puzzleman
Le jeu existe dans deux configurations remarquables : Un cube, et un robot de type androïde. S’il est relativement facile de passer du premier au second, l’inverse est nettement moins aisé.



IQ fit
Les formes et couleurs du jeu attirent le regard, et même les plus jeunes s’y essayent. Sans forcément arriver jusqu’au bout (« c’est trop difficile ») mais de toute manière avec le plaisir de la recherche et de la manipulation.




Fer
Le jeu du fer à cheval
Un joueur a deux pions blancs, l’autre a deux pions jaunes. Au début du jeu, chaque joueur garde ses deux pions dans la main. Puis
- le premier joueur pose un des deux pions blancs sur un des 5 sommets du graphe ;
- le second joueur pose un des deux pions jaunes sur un des 4 sommets restants (on ne peut pas poser un pion sur un sommet déjà occupé) ;
- le premier joueur pose son second pion blanc sur un des 3 sommets libres ;
- le second joueur pose son dernier pion jaune sur un des 2 sommets encore disponibles :

À ce moment du jeu, il ne reste plus qu’un sommet du graphe encore libre. Alors les deux joueurs, chacun son tour, glissent un de leurs pions vers le sommet vide, depuis un sommet adjacent : Voici 4 mouvements du jeu, qui aboutissent à un échange de deux pions en passant par le centre du graphe :

Si, à un moment du jeu, un des joueurs ne peut plus déplacer un pion parce que le sommet vide n’est adjacent à aucun de ses deux pions, il a perdu le jeu. Sinon, il y a partie nulle. Mais ça peut durer longtemps avant qu’un joueur trouve un moyen d’exploiter une faille de son adversaire, sans commettre une faille lui-même. D’où l’intérêt du jeu de la madelinette, dans lequel ce genre de partie nulle est moins fréquent.
Madelinette
Le jeu de la madelinette
L’un des joueurs prend les trois nazgûls dans sa main, l’autre joueur prend les trois licornes. Ensuite
- le premier joueur pose un nazgûl sur un des 7 sommets du graphe ;
- le second joueur pose une licorne sur une des 6 sommets libres ;
- le premier joueur pose le second nazgûl sur un des 5 sommets libres ;
- le second joueur pose sa deuxième licorne sur un des 4 sommets libres ;
- le premier joueur pose le dernier nazgûl sur un des 3 sommets libres ;
- le second joueur pose la dernière licorne sur un des deux sommets non encore occupé.
Une fois les trois nazgûls et les trois licornes posées, il ne reste qu’un sommet libre. Le premier joueur va alors glisser un nazgûl vers l’unique sommet libre. Mais à condition de pouvoir le faire, par exemple ici le sommet libre n’est accessible qu’aux licornes et le premier joueur a perdu :
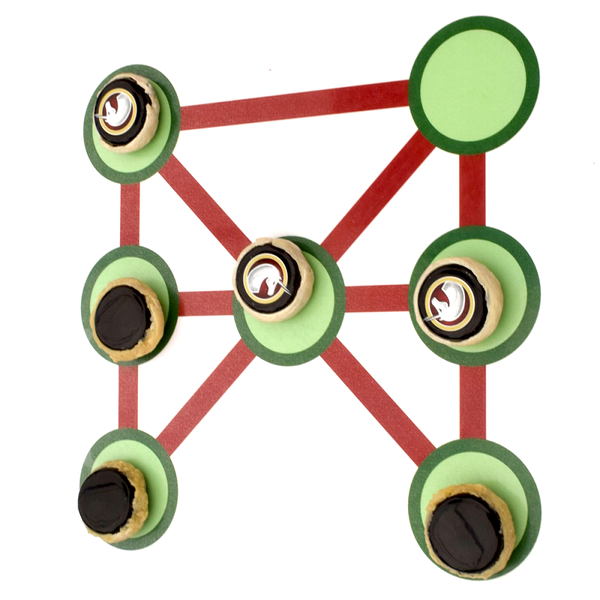
Sinon, chacun son tour bouge un jeton depuis le sommet où il se trouve jusque vers le sommet libre, en empruntant une arête du graphe. Par exemple voici un coup joué par les licornes :

Le premier joueur qui ne peut plus bouger a perdu le jeu. Ci-dessous, lequel va gagner ?

C’est aux nazgûls de jouer, mais ils sont bloqués : Les licornes ont gagné :

Craie
Les triangles de Sierpinski restent populaires et leur tracé permet à des street geometers de plus en plus jeunes de s’appliquer :




Le dégradé à la craie donne un aspect artistique au résultat :



On va même de plus en plus loin, avec invasion du parking de l’université par des jeunes traceurs de triangles :

Idem pour l’intégramme « zistoir maron »

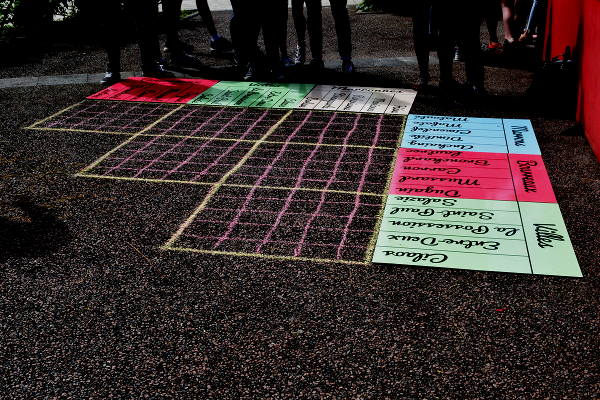




Parkings
Le jeu des deux parkings reste l’un des plus populaires depuis sa création il y a deux ans :

Cette popularité est telle qu’il a fallu créer d’autres pions pour un second exemplaire :

Ici les rouges viennent d’occuper le sommet central, très prisé :

Les bleus cherchent alors également un moyen d’occuper ce sommet :
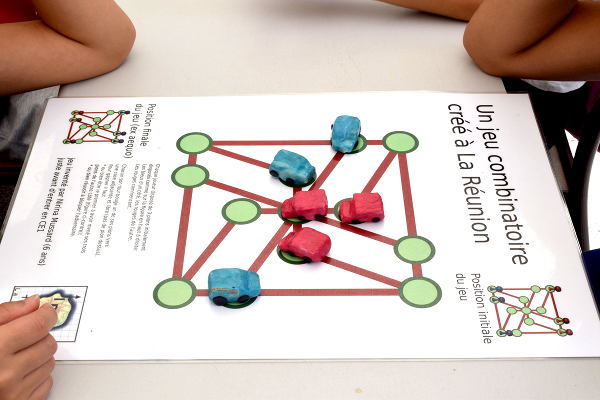
L’occupation du sommet central permet aux rouges de bloquer une des voitures bleues :
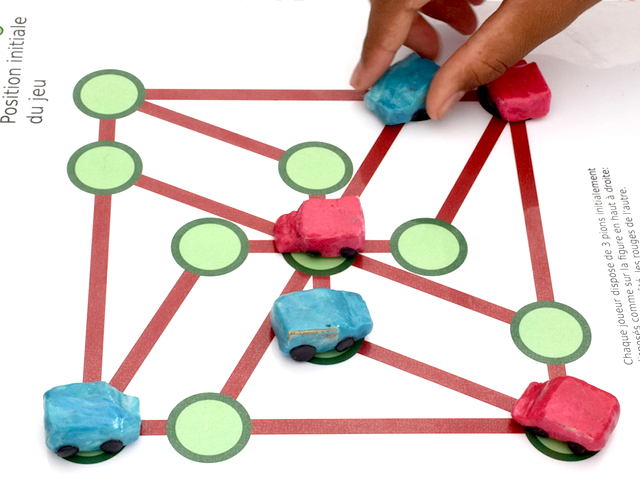
et ici, aux bleus de bloquer une voiture rouge :
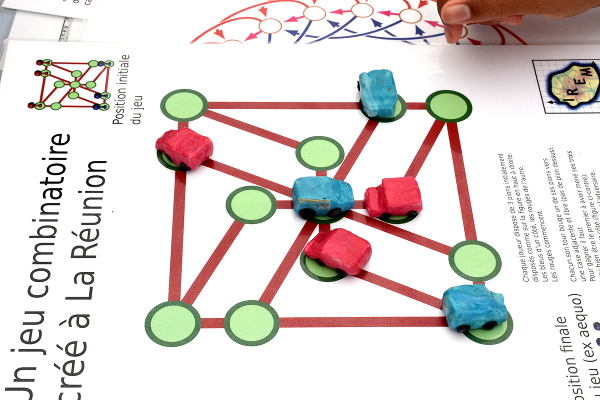
Dans les deux cas, cela ne donne pas pour autant une victoire immédiate, puisqu’il reste encore deux autres voitures à bloquer.
Ici, une erreur des rouges permet aux bleus de gagner en deux coups. Voyez-vous comment ?
Voici une typique situation bloquante pour les rouges :
- Si les rouges avancent la voiture en haut à droite, les bleus gagnent la course en un coup, puisque deux voitures bleues sont déjà en place et la troisième est à une arête de l’arrivée ;
- Si les rouges n’avancent pas cette voiture, ils ne pourront jamais gagner, car la voiture doit aller à sa destination qui est à gauche.
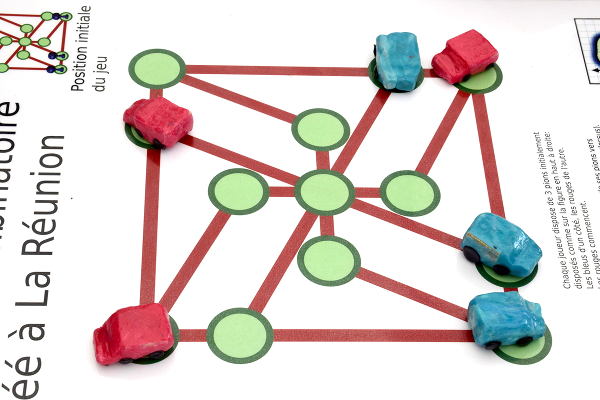
Voici une autre situation typique, cette fois-ci les rouges ont gagné en menant en premier leurs trois voitures au bout

Et cette autre victoire des rouges, si elle est moins typique, est plus intéressante, car les bleus ne peuvent pas bouger alors que c’est à leur tour de jouer :
Une variante de ce jeu est décrite en conclusion de cet article.
Tangue
Le jeu de chiens et tang garde son succès. Voici les chiens et le tang au départ, prêts à en découdre :
Le jeu a commencé, le tang ayant effectué le seul mouvement qu’il pouvait, et l’un des chiens ayant avancé :

Ah cette fois-ci les chiens ont gagné :

Le succès du jeu a eu raison du tang, à qui il a fallu faire un pansement pour pouvoir continuer à jouer avec :
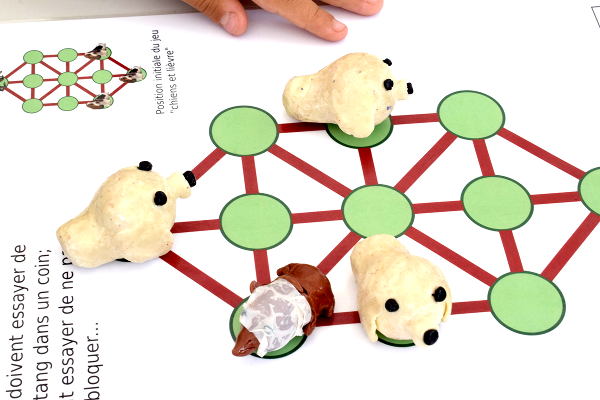
On peut jouer en ligne si on souhaite s’entraîner.
Nim
Le moment le plus intéressant est celui où on est à la fois déçu d’avoir perdu et émerveillé de savoir pourquoi on a perdu :

Ici, il s’agit du jeu de Nim sur un triangle, et le pion est arrivé au bout (sur un des côtés du triangle). Chaque mouvement du pion est imposé et comme il reste un nombre impair de flèches à franchir, l’issue du jeu est déterminée.
Voici le jeu « soustrais un carré », dont le graphe représente des soustractions possibles effectuées sur une variable entière (une soustraction est modélisée par une flèche sautant un certain nombre de sommets) :
- les flèches magenta représentent la soustraction de 1 ;
- les flèches rouges représentent la soustraction de 4 ;
- les flèches bleues représentent la soustraction de 9 ;
- les flèches vertes représentent la soustraction de 16.
Les nombres 1, 4, 9 et 16 étant des carrés, on comprend le nom du jeu.
Une joueuse vient d’emprunter la flèche rouge allant de 4 à 0, et gagne ainsi le jeu :

Venant de commencer le jeu, la même joueuse a utilisé la flèche bleue pour soustraire 9 à 20, aboutissant alors à 11 :

Mal lui en a pris : Son adversaire joue aussi la flèche bleue ce qui mène le pion à la case 2, et elle n’a pas d’autre choix que d’aller à la case 1 (flèche magenta) ce qui permet à son adversaire faire pareil et gagner à nouveau le jeu.
Si on « colorie » récursivement en bleu les cases gagnantes et en rouge les cases perdantes, on obtient la stratégie gagnante par coloriage :

... mais à condition de bien colorier, ici il y a eu une erreur d’induction : Au début les couleurs rouge et bleu s’alternent, mais ensuite ce n’est plus le cas.
Puzzles
Le jeu Curvica lui aussi touche les plus jeunes, qui affichent une persévérance et un taux de réussite surprenants :

Mais qu’est-ce qui se passe ici ?

Que font ces élèves de Terminale et de CE2 ?

En fait, les premiers expliquent la numération binaire aux seconds

avec un tel succès que même l’abaque de Gerbert, pourtant très populaire, est déserté au profit du puzzle :

Il faut dire que les élèves ont adopté une tenue voyante pour attirer le jeune public vers le stand quelque peu isolé de l’IREM :

Voici le résultat de l’addition 24+5 (24 en jaune, 5 en cyan, la somme 29 en noir) :

Le même résultat, mieux visible :
Puis l’addition de 17 (en jaune) avec 23 (en cyan), en cours de calcul :

Au Tampon, les élèves de cycle 3 ont préféré commencer par additionner 0 à 0 pour mieux comprendre le principe :

L’apprentissage de la numération binaire semble, à l’école primaire, à la fois simple et ludique :

Mais surtout, c’est la manipulation qui est en vedette :

Nomogrammes
Ce qu’il y a de bien avec la nomographie, c’est que l’on peut voir le calcul en train de s’effectuer (ici, par une élève de cycle 3) :
Calcul de 8×2 sur un nomogramme :

Calcul de 10×8 sur un autre nomogramme :

Le même calcul 10×8 sur un autre nomogramme hyperbolique :

Le calcul de 4×8 sur la parabole de multiplication :

Nouveautés 2018
Pour la fête de la science 2018, de nombreuses nouveautés sont apparues. La plupart d’entre elles sont décrites dans les onglets suivants (une place particulière a été réservée en fin d’article à la dernière nouveauté) :
Hanoi
Une autre nouveauté de l’IREM est les tours de Hanoi :


Cryptographie
La manipulation du disque codeur (chiffre de Cesar) permet une approche singapourienne de la cryptographie, et partant de là, de l’arithmétique modulo 26 :

Mafate
Le facteur de Mafate n’est pas une nouveauté, mais sa commercialisation par Asco & Celda, si. L’apparition sur le marché devrait avoir lieu début 2019, et François Barbé est venu avec un prototype similaire à ce qui sera vendu :

Le jeu sera vendu en pièces détachées, et le premier plaisir de l’enfant qui le recevra en cadeau, sera d’assembler les pièces du jeu (les tours). Ensuite, pour construire un circuit, les pièces grises seront assemblées à la main, ce qui fait que l’enfant aura manipulé avant même de jouer.
En plus, il y a une version à deux joueurs :

Comme au jeu de Shannon, les rôles des deux joueurs sont asymétriques : Le facteur de Mafate veut aller au bout du circuit, et a donc pour charge de construire le chemin, alors que l’autre joueur veut empêcher le facteur de faire sa tournée, et veut donc créer des impasses. On peut donc considérer que ce jeu est un jeu de graphe (comme l’est celui de Shannon).
La manipulation est très présente dans ce jeu :


Ci-dessus un joueur place le facteur de Mafate sur une tour de hauteur 9, ce qui lui permet par un escalier de hauteur 2, d’atteindre la tour de hauteur 7.
Ci-dessous deux joueurs se demandent où placer les tours de hauteur 8 et 9, l’un pour établir un chemin permettant au facteur d’atteindre la tour de hauteur 10, l’autre pour l’en empêcher :


Comme pour chaque activité basée sur la manipulation, le simple fait de tripoter l’objet entre ses doigts, peut servir de support à la réflexion :

Cass’coco aussi a été présenté à nouveau, et là encore on manipule beaucoup, à tout âge :



Nomogramme
Une autre nouveauté est la construction d’une parabole de multiplication en grand, à la craie : Pour les facteurs on n’a tracé que les points à coordonnées entières sur la parabole, et pour lire le produit on a interpolé les graduations allant de 10 en 10 (autrement dit, le repère n’est pas orthonormé).
Pour calculer 5×11, on commence par placer une extrémité de corde sur le point 5 (premier facteur) :

puis on tend la corde jusqu’à la graduation 11 (second facteur) :

et on constate que la corde coupe l’axe des produits exactement entre les graduations 50 et 60 :

ce qui montre que 5×11=55, avec une précision intéressante.
De même pour calculer à l’aide de cette parabole la produit 13×13, on positionne les deux extrémités de la corde sur les points numéro 13 des deux branches de la parabole :

et on constate que la corde passe juste en-dessous de la graduation 170 :

Là encore on voit que le produit 169 est obtenu avec une bonne précision
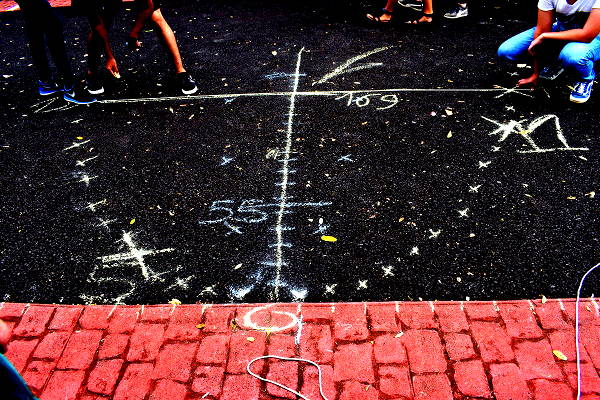
et on marque la graduation 169 sur l’axe des produits. Mais de façon éphémère, la pluie ayant rapidement effacé la craie.
Rover
Une autre nouveauté cette année a été l’utilisation de la robotique pour la mise en application de la trigonométrie.

Tout d’abord il y a le Rover, qui peut être programmé depuis la calculatrice pour effectuer des déplacements :

La calculatrice est fixée sur le dessus du Rover.
Voici à quoi ressemble un programme de parcours d’hexagone :
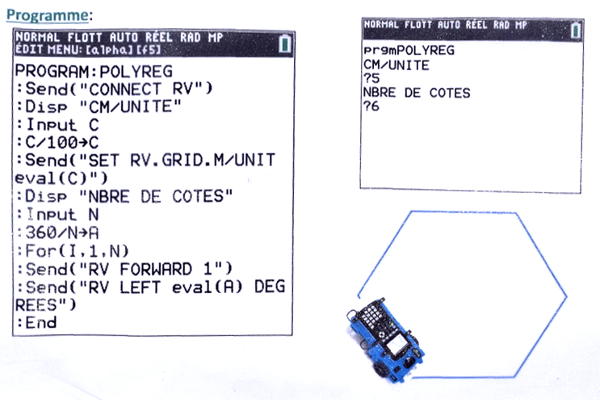
On se creuse la tête en groupe pour trouver quels sont les polygones réguliers que l’on peut faire tracer au Rover sur une surface plane :

Et le innovator hub lui aussi connecté à la calculatrice mais muni de capteurs, notamment un télémètre, permettant de mesurer une distance :

A la recherche de l’angle du jour (13/11/18) : 42° évidemment !
Sur cette photo on voit le dispositif permettant de mesurer la distance entre le capteur (à droite) et le talon en bois :

Comment alors peut-on mesurer un angle, à partir de cette mesure de distance ?
Voici une figure DGPad que l’on peut manipuler pour comprendre l’alogirthme :
Et quand on a fini la manip, on peut vérifier avec une mesure de l’angle par l’accéléromètre du smartphone :

Le petit boîtier reliant la calculatrice au capteur de distance émet un son de fréquence variable. Cette fréquence sonore émise est une fonction décroissante de l’écart à l’angle recherché.
- Une simulation GeoGebra du dispositif :
- Le fichier de la simulation ci-dessus :
- Et la version DGPad ci-dessus :
Fanorona
Le jeu dit de Fanorona à 3 rangées est en réalité la marelle à 6 pions (trois par joueur) : Chacun son tour pose un des ses pions puis les fait glisser jusqu’à l’obtention d’un alignement.

Ce jeu, connu dans le monde entier sous des noms divers, a la réputation à Madagascar de servir d’entraînement pour le vrai fanorona, où il s’agit plutôt d’éviter les alignements, qui peuvent être pris par approche ou par éloignement : Il suffit que deux pions soient adjacents pour permettre la prise du plus anciennement placé d’entre eux.
Voici le jeu au départ :

Le premier coup a été joué par les rouges : Le jeton qui était vers le bas à gauche a avancé en diagonale sur le centre du plateau, ce qui l’a fait suffisamment approcher de deux jetons bleus, et a permis de les prélever tous les deux (car ils étaient alignés) :
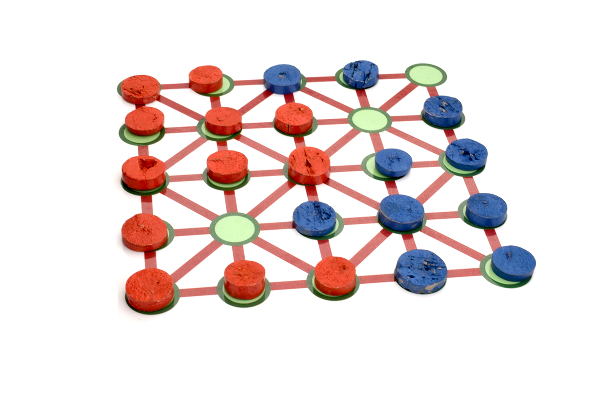
En avançant un jeton bleu, le joueur de droite peut prendre, par approche, le jeton rouge qui est tout à gauche de la photo :

Mais il aurait pu jouer mieux puisque les trois jetons rouges du centre sont alignés et pouvaient être pris d’un seul coup. D’ailleurs la joueuse qui a les rouges va lui prendre trois pions d’un coup, on les voit vers le bas de la photo.
Nim
Les nouveaux jeux de Nim sont dûs à Aviezri Fraenkel. Ils diffèrent des anciens par le fait qu’il y a plusieurs jetons ; mais chaque joueur peut déplacer n’importe quel jeton parmi ceux qui sont encore mobiles, il n’y a pas de jetons réservés à un joueur ou à l’autre (sauf pour Arrows présenté dans un autre onglet).
Le jeu « beat Craig » se joue avec 4 jetons sur un graphe orienté :
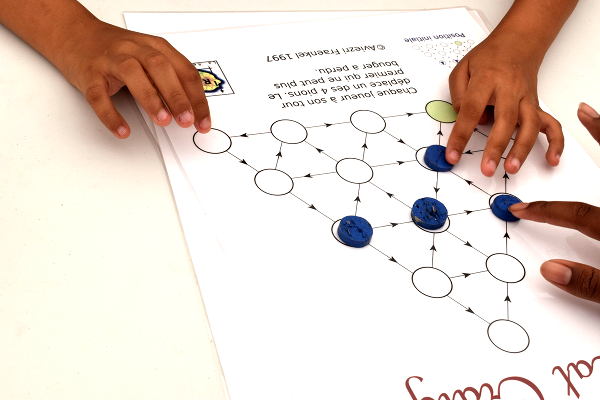
Le sommet du graphe colorié en vert (en haut de la photo) est un puits (ou arrivée ou trou noir) : Une fois qu’un jeton y est arrivé, il ne peut plus en sortir parce qu’il n’y a aucune flèche sortant de ce sommet. Ce qui fait que le gagnant du jeu est celui qui mène le quatrième jeton dans le puits : Son adversaire ne peut plus jouer, et perd ainsi le jeu.
Le jeu « beat Doug » est du même type, sauf qu’il ne comporte pas de cycle et il est donc plus facile à analyser. Fraenkel propose aussi un « grand Craig ».
Le jeu « Jupiter et la comète » n’est pas un jeu de Nim, puisque lorsque deux jetons se rencontrent ils s’annihilent. Le plateau de jeu est assez impressionnant :
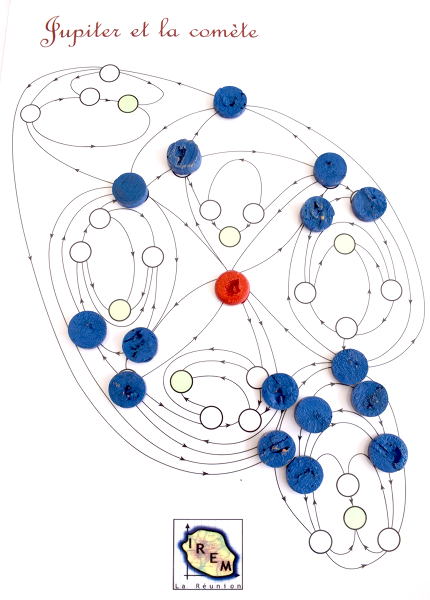
Arrows
Le jeu Arrows n’est pas nouveau puisqu’Aviezri Fraenkel et Eggleton le commercialisaient dès les années 1990, mais son apparition à l’IREM date de la rentrée 2018. Le plateau de jeu est assez beau pour attirer tous les regards :

Le jeu fait souvent penser aux échecs : On prend un pion adverse en prenant sa place, et on verra plus bas quelques tactiques assez similaires à celles qui existent aux échecs.
Ici, le jeton bleu qui vient d’une case jaune (centrale, sans flèche), en arrivant sur une case rouge, menace un jeton rouge qui est au bout de la flèche. Ce jeton rouge, par déplacement, va alors à son tour menacer le jeton bleu :

Certes, le jeton bleu peut suivre le jeton rouge pour continuer à le menacer, mais à l’étape suivante, le jeton rouge menacerait deux jetons bleus simultanément et il ne serait plus possible de les préserver tous les deux. Cette situation ressemble à une fourchette (échecs) :

Ci-dessus le joueur Bleu retire un de ses jetons pour échapper à la menace du jeton rouge, mais l’autre jeton bleu restera alors à la merci de Rouge, qui prend alors un avantage sur Bleu.
De façon générale, les débutants jouent plus souvent défensif qu’offensif. D’autant plus que lorsqu’il n’y a pas de flèche, on peut glisser dans les deux sens, et cela n’est pas toujours perçu par les joueurs. Par exemple, ici, le jeton bleu peut aller dans les deux sens :

Mais les joueurs ont parfois du mal à voir ces mouvements possibles [1]. Ici le jeton bleu fait un mouvement inutile alors que deux jetons rouges peuvent être pris, et la prise de l’un d’entre eux est même nécessaire puisqu’ils constituent une menace :

Ici c’est Rouge qui ne sait pas trop quoi faire alors que deux de ses jetons sont menacés :

Les fins de partie aussi ressemblent aux échecs, avec l’avantage numérique dont peut profiter un joueur. Ici les bleus ont un avantage sur les rouges (4 jetons contre 3) :
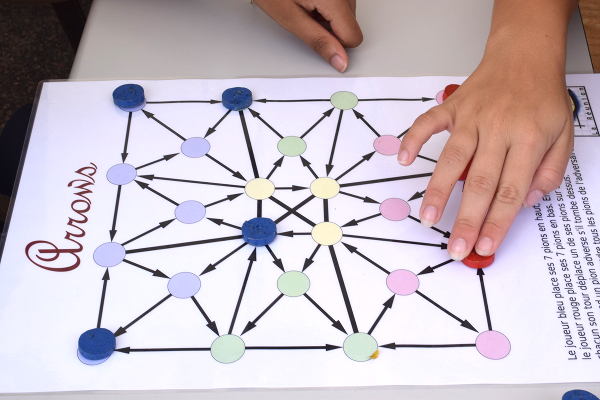
S’ils maintiennent leur avantage :

ils gagneront en bloquant l’unique pion rouge dans un piège qui n’est plus à la portée des rouges parce qu’ils n’ont plus qu’un jeton.
Snort
Le jeu de Snort se joue sur un graphe non orienté. L’un des joueurs colorie les sommets de ce graphe en bleu, l’autre colorie les sommets en rouge. Le coloriage se fait chacun son tour, mais
- il est interdit de colorier un sommet déjà colorié ;
- il est interdit d’avoir deux sommets à la fois adjacents et de couleurs différentes.
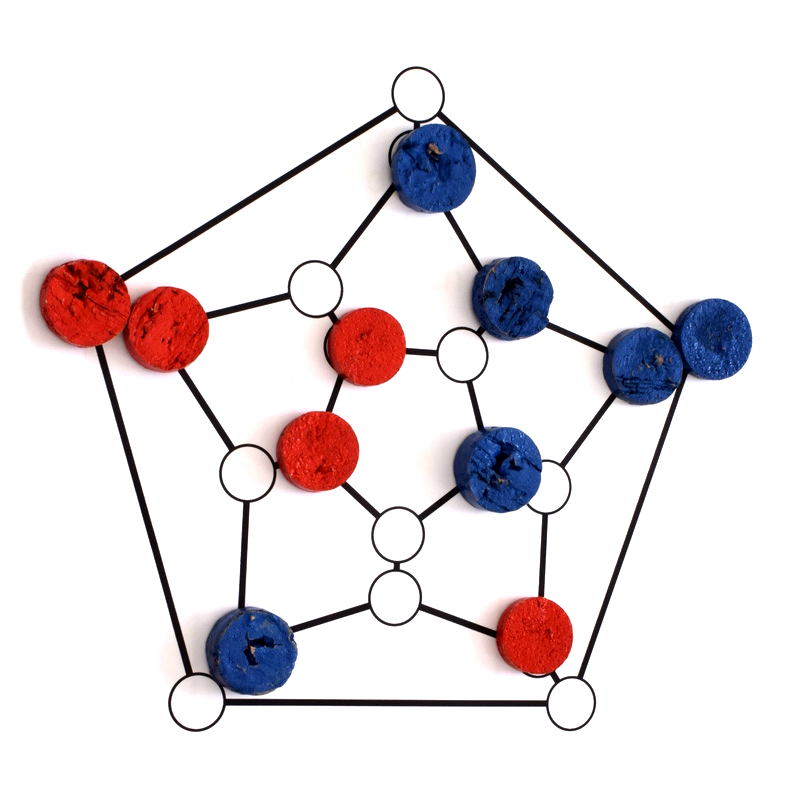
Pour économiser les graphes, on pose des pastilles bleues et rouges sur les sommets, en guise de coloriage provisoire. Voici trois parties de Snort, jouées simultanément par des groupes de visiteurs :

Sur le graphe ci-dessous, 4 sommets ont déjà été coloriés, 2 en bleu et 2 en rouge. Les 4 sommets blancs en bas à gauche ne peuvent plus être joués par bleu parce qu’ils sont adjacents à du rouge :
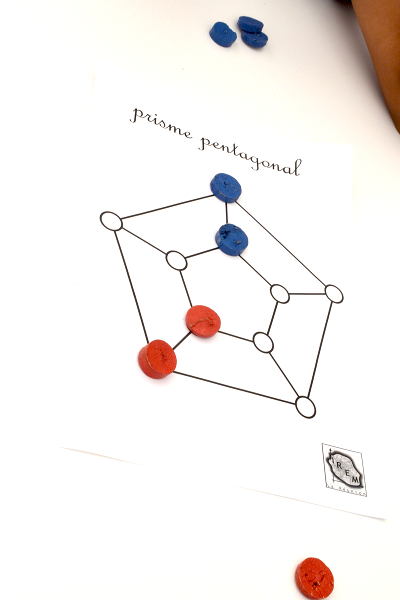
En fait il ne reste plus que deux sommets coloriables en bleu, ce sont ceux qui sont en haut à droite. Bleu colorie le plus central d’entre eux :

Du coup il ne reste plus qu’un sommet blanc non adjacent à du bleu, et Rouge est obligé de jouer celui-là :

Et là c’est la grosse surprise pour Bleu : Chacun des 4 sommets non encore coloriés est adjacent à un sommet rouge, et Bleu ne peut colorier aucun d’entre eux en bleu. Pourtant c’est à son tour de jouer : Il a perdu le jeu !
Voici une autre partie terminée sur le graphe ci-dessus, cette fois-ci gagnée par Bleu qui a joué finement :
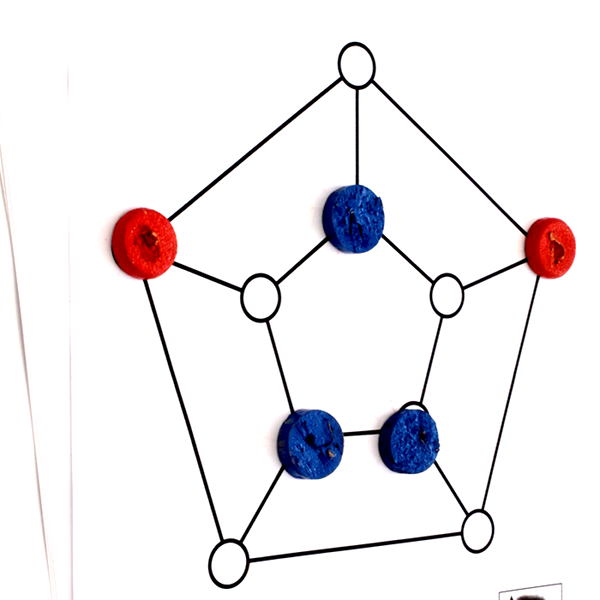
Et une autre fin de partie, les deux derniers coups étant montrés sur le graphe de Frucht :
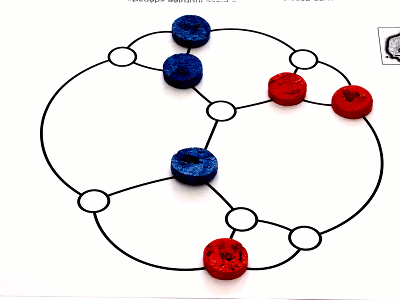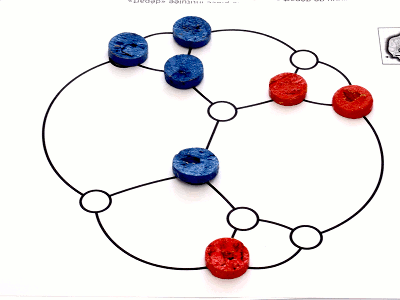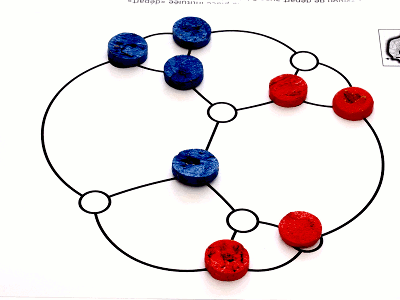
Comme le dernier sommet colorié est rouge, Bleu ne peut plus colorier de sommet et c’est encore lui le perdant de ce jeu.
Toujours sur le graphe de Frucht, c’est Rouge qui gagne cette partie :

et Bleu qui gagne celle-là :

Bleu a déjà posé 4 jetons et Rouge seulement 3 : On voit que c’est au tour de Rouge de jouer ; mais chaque sommet blanc étant adjacent à au moins un sommet bleu, Rouge ne peut pas jouer et a donc perdu. Mieux encore, Bleu, ayant oublié que ce n’est pas à son tour de jouer, commence à colorier un 5e sommet en bleu : Même si c’était à lui de jouer, Bleu pourrait encore le faire. Selon la théorie de Conway, cette position de jeu a pour valeur 1 (avantage à Bleu, quantifié par un coup).
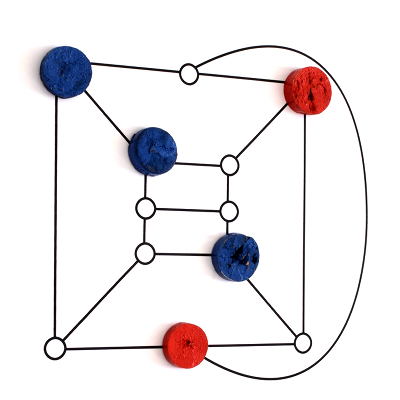
C’est Bleu qui gagne ici sur le cube de Bidiakis :
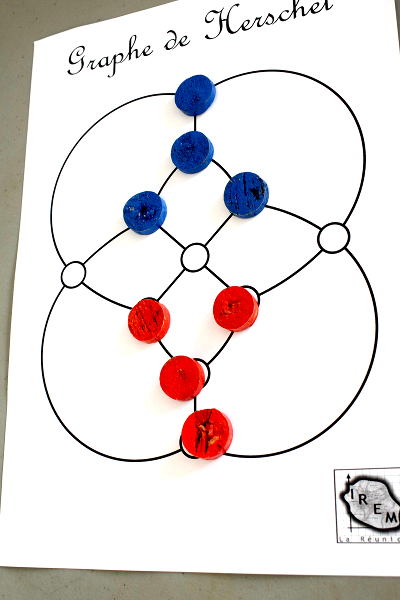
Et sur ce graphe de Herschel c’est Rouge qui a gagné :
Enfin, une partie gagnée par Bleu sur le graphe du dodécaèdre :
Gerbert
Une attraction qui a bénéficié d’un succès particulier, est la présentation de l’abaque de Gerbert. Ce sont essentiellement des élèves de cycle 3 qui en ont bénéficié ; au Moufia :

ou au Tampon :

Pour additionner 950 avec 47, il est d’abord nécessaire de poser les deux nombres 950 et 47 sur l’abaque ; d’abord 950 (seuls deux jetons sont nécessaires, le chiffre zéro n’existant pas sur l’abaque de Gerbert) :

puis le ④ des dizaines :

et le ⑦ des unités :

Pour additionner ⑤ et ④ (ou plutôt 50 et 40, puisqu’on est dans la colonne des dizaines), Gerbert préconisait un remplacement (on enlève les jetons ⑤ et ④, on met un jeton ⑨ à la place). Ce remplacement n’est pas un automatisme chez les élèves de CM2 qui essayent plutôt de simuler un calcul écrit avec l’abaque de Gerbert :

Une fois le remplacement effectué, le résultat de l’addition apparaît : 997. Après cela, a été proposé d’additionner 6 à ce résultat. Tout d’abord, en empilant les jetons ⑦ et ⑥, ensuite, en ajoutant les jetons ① et ③ les remplaçant :

enfin en enlevant le tas de deux jetons ⑥ et ⑦. Ce qui permet de finir l’addition en remplaçant les jetons ⑨ et ① dans la colonne des dizaines, par leur équivalent (un seul jeton, ①, mais dans la colonne des centaines) puis recommencer la manœuvre pour additionner 900 avec 100.
Voici une autre addition, avec retenue cette fois-ci : 974+57.
Tout d’abord, il s’agit de remplacer les deux jetons ④ et ⑦ de la colonne des unités, par deux jetons ① à placer entre les deux colonnes des dizaines et des unités. Ceux-là sont en bas, on le les voit pas sur la photo . On passe ensuite à l’addition entre 70 et 50 , en commençant par empiler les jetons ⑤ et ⑦ :

puis en remplaçant cette pile par deux jetons ① et ② :

ensuite, en s’occupant de la retenue : Il reste à calculer 20+10 (la retenue) en empilant les jetons ① et ② de la colonne des dizaines :

puis en les remplaçant par un jeton ③ (toujours dans la colonne des dizaines) ; enfin, en menant de façon similaire l’addition 900+100, ce qui donne le résultat :

On remarque que l’absence de chiffre 0 oblige à « mettre un haut-parleur sur sa pensée » pour connaître le résultat : 1 millier, 3 dizaines et 1 unité se lisent « mille trente et un ».
Des élèves ont été déroutés par l’absence de jeton portant le chiffre 0 (c’était prévisible) mais aussi, ce qui est plus surprenant, de jetons portant des signes d’opérations comme + ou × : Ils cherchent à imiter l’écrit avec l’abaque.
Voici l’abaque au format pdf :
Noter que le verso n’a pas été utilisé lors de la fête de la science, alors qu’il permet de faire des calculs sur les nombres décimaux. C’est essentiellement par manque de temps que seul le recto a été présenté, et qu’une seule multiplication a pu être menée (en CM2).
Petri
Pour jouer sur un réseau de Petri, chaque joueur à son tour active une transition. Au départ du jeu, il y a des jetons uniquement sur la place de départ, et le premier joueur choisit une des transitions franchissables et l’active. Ici, la transition choisie (en bas, le carré gris) absorbe un jeton du départ et en injecte 2 (car il y a 2 flèches) dans la place suivante :

Après l’activation de cette transition, il y a donc un jeton de moins au départ (puisqu’il a été absorbé par la flèche allant du départ à la transition) et deux jetons (injectés par la transition) dans la place du bas (en bas à droite, le cercle bleu qui est maintenant occupé par 2 jetons).
Le second joueur choisit la transition du milieu ; elle absorbe un des trois jetons restant au départ, puis injecte un jeton sur la flèche allant au centre :
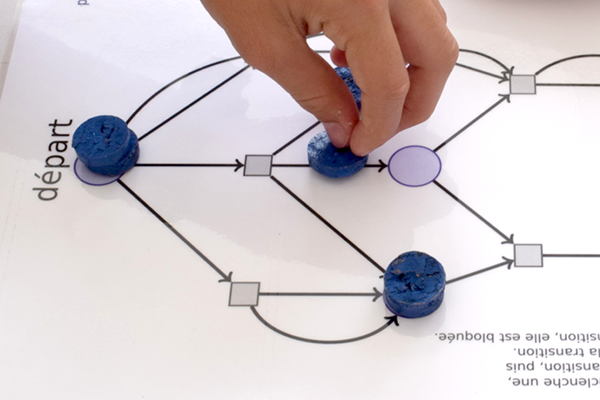
puis un jeton sur chacune des autres flèches :

Enfin, les jetons vont au bout des flèches, ce qui aboutit à cette situation :

Les deux places du haut étaient vides et se sont vu injecter un jeton chacune, elles sont donc maintenant occupées par un jeton chacune. La place du bas, qui était déjà occupée par 2 jetons après le premier mouvement du jeu, en a accueilli un de plus et est maintenant occupée par 3 jetons.
La transition en haut à droite ne peut être activée parce que pour cela elle devrait pouvoir absorber deux jetons depuis la place du haut, laquelle à ce stade ne contient qu’un jeton, ce qui est insuffisant. Le premier joueur (dont c’est le tour de jouer) choisit alors la transition en bas à droite. Celle-ci absorbe un jeton de chaque place menant à icelle, ce qui laissera un seul jeton en bas (sur les deux présents) et videra le jeton du milieu :

Ensuite la transition va injecter un jeton dans la place à laquelle elle mène :
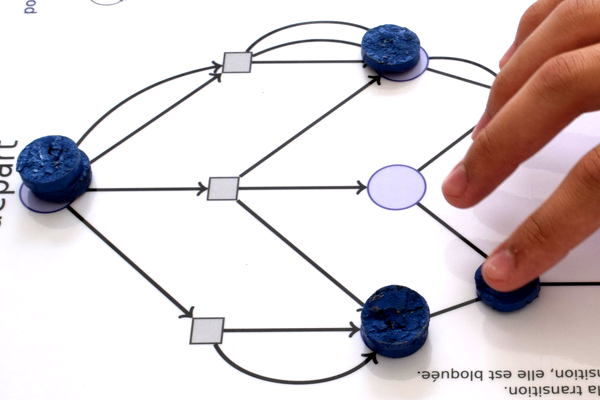
ce qui donne la situation suivante :

On voit que les trois transitions à droite sont « mortes » (ne peuvent être déclenchées) parce que chacune d’entre elles a au moins une place vide en amont. Mais les trois transitions du départ sont encore vivantes, et le second joueur choisit celle du haut. Celle-ci va absorber les deux jetons restant au départ puis injecter 3 jetons dans la place d’en haut, ce qui ramène à 4 le nombre total de jetons qu’elle contient :

Malgré cette abondance de jetons, plus aucune transition n’est encore jouable puisque chaque transition est bloquée par au moins une place vide en amont de celle-ci. Le réseau de Petri est dit « mort » et le premier joueur ne peut plus jouer : On convient qu’il a perdu le jeu. Ce qui amène aux questions suivantes :
- Avec 4 jetons au départ, le premier joueur pouvait-il gagner ?
- S’il y a n jetons au départ, peut-on savoir qui gagne le jeu ?
- À quoi ressemble un réseau de Petri sur lequel les chances de gain sont les plus équilibrées possibles, entre les deux joueurs ?
Pour aider à explorer ce jeu, voici
- un article sur les réseaux de Petri
- un utilitaire de jeu sur réseau de Petri ;
- le jeu à imprimer (les jetons ne sont pas fournis) :
Mathésport
Après 4 journées intenses de présentation de tous ces ateliers à un public captivé et nombreux, au moment où la fête de la science était censée finir, une nouvelle activité est apparue en quelques instants, le mathésport où l’on bouge autant qu’on réfléchit :
Graphe
Pour commencer, une copie du graphe des deux parkings a été faite à la craie sur le goudron :

Ensuite des joueurs ont été sollicités, pour se grouper en deux équipes de 3. Au départ, chaque joueur est sur un sommet du graphe, chaque équipe étant alignée d’un côté du graphe. Ensuite, chacune son tour, les équipes déplacent un de leur joueur d’un sommet vers un sommet à la fois adjacent et libre. C’est le capitaine de l’équipe qui décide, s’il n’y a pas de consensus, qui bouge, et vers quel sommet.
La première équipe dont les trois membres occupent les sommets adverses, peu importe dans quel ordre, a gagné le jeu.
Match1
Mathématiques et abdominaux font bon ménage !
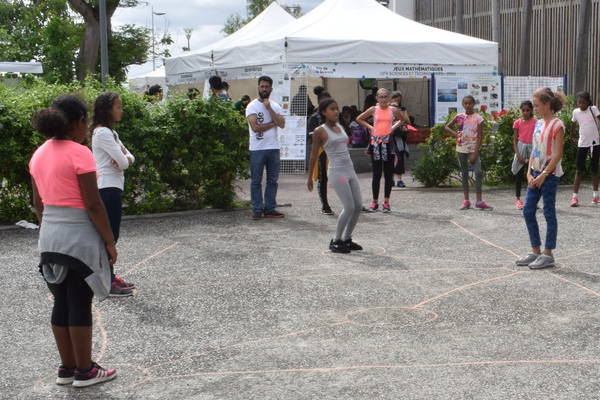
Le port de tennis est recommandé pour faire des maths avec Pacom

La tactique de la capitaine de l’équipe se met en œuvre avant même la fin du mouvement :
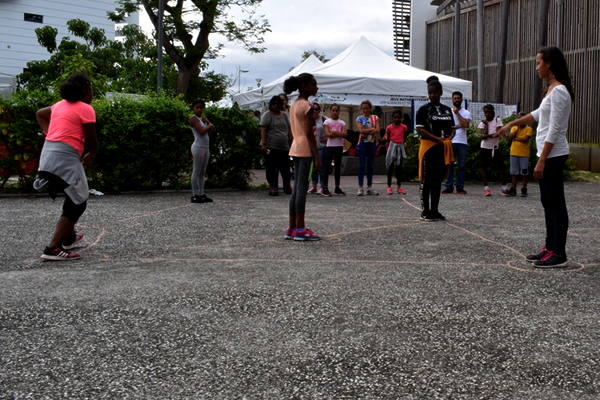
Avant de bouger elle-même, la capitaine de l’équipe fait avancer les autres. Cette tactique explique-t-elle qu’elle ait si souvent gagné ?

Les mouvements évoquent parfois la marelle :

Match 2
Puis ce fut un match entre deux équipes de filles :


Les gestes de la capitaine de l’équipe sont précis et réfléchis :


Match 3
Cette fois-ci ce sont deux équipes de garçons qui s’opposent :



Match 4
Les gagnants affrontent une équipe de filles :





Les commentaires vont bon train :

Match 5
Visiblement, la fin de ce match est axée sur la notion de blocage (des garçons par les filles) :

Les gagnantes affrontent alors les animateurs IREM :


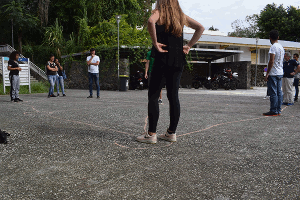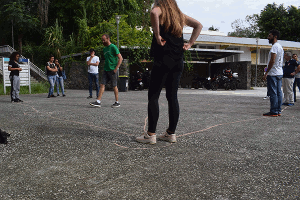
Match 6

Situation rare : Seule la moitié du graphe est occupée :




Encore une fois, seule la moitié du graphe est occupée :

Les trois gagnants ont ensuite « affronté » une équipe d’animateurs IREM :


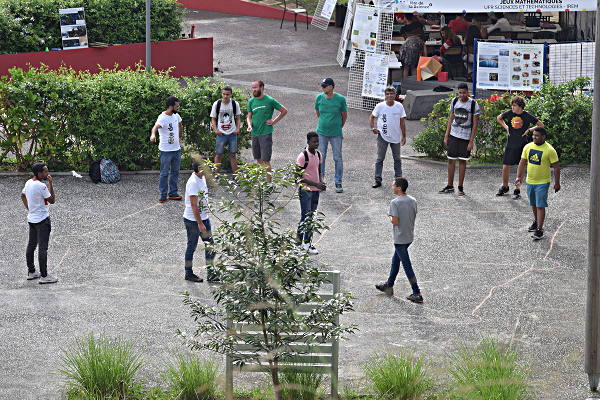
Match 7
Deux équipes d’animateurs IREM analysent le jeu en jouant (c’est encore la meilleure manière) :



Et c’est parti pour un nouveau match, en mode introspection :

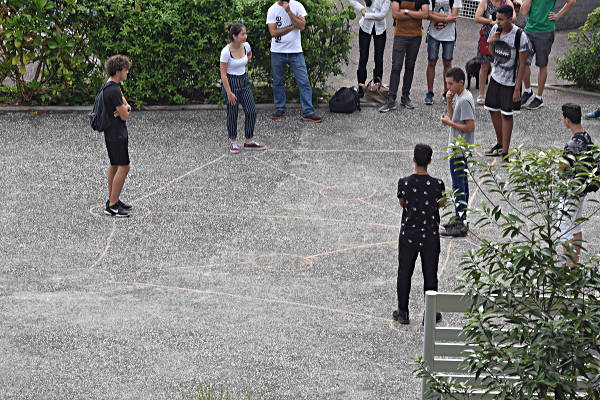
Match 8
Il s’agissait moins de faire un vrai match, que d’explorer le jeu afin d’améliorer ses règles, notamment pour chercher comment éviter les matchs nuls

Les animateurs de l’IREM contribuent :


Comme à la pétanque et au football, les commentaires des spectateurs vont bon train :

Même les joueurs ont leurs commentaires à faire :

Conclusion
Une fois que le service d’ordre de l’université a enfin réussi à expulser les mathésportifs, ce fut le temps de la troisième mi-temps, bien évidemment consacrée à une analyse du jeu des deux parkings :

Pour en savoir plus sur ce jeu, voir cette analyse.
Une décision a été prise aussi pour la prochaine fois : Un graphe encore plus grand, dans une forêt, de manière qu’aucun joueur ne voie les autres si ce n’est par GPS.



























































Commentaires