Algèbre et barycentres

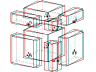
Celui-ci est magique : Un puzzle reconstituant un cube, qui montre le produit remarquable $(a+b)^3=a^3+3a^2b+3ab^2+b^3$ :

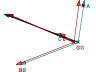
Ici on déplace dans l’espace un point $G$, avec des curseurs correspondant à ses coordonnées ; on voit alors le vecteur $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$, ce qui permet de trouver l’unique position de $G$ qui annule ce vecteur, et de vérifier qu’alors A, B, C et G sont coplanaires : On est passé à un problème de géométrie plane. On remarque que pour déplacer G, on manipule des curseurs, ce qui ne serait pas le cas dans un vrai logiciel de géométrie dans l’espace (avec une interface Wii ?) ; existe-t-il un vrai logiciel de GD dans l’espace ?

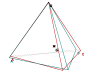
Ensuite (terminale S) on vérifie que l’ensemble des barycentres des sommets d’un tétraèdre à coefficients positifs est l’intérieur du tétraèdre (les curseurs servent à modifier les coefficients barycentriques) :

Enseignement de spécialité en terminale S

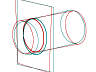
Sont au programme, les sections de cônes et de cylindres par des plans parallèles aux axes de coordonnées. Alors on commence par les sections d’un cylindre par des plans parallèles à son axe :

puis par des plans perpendiculaires à son axe :

Ensuite des sections d’un cône par des plans perpendiculaires à son axe :

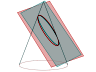
et par des plans parallèles à son axe ; seule une partie du cône est dessinée mais l’hyperbole est complète :

Il serait dommage bien que ce ne soit pas au programme de ne pas évoquer les sections d’un cône par des plans de direction quelconque : Ici le curseur ne déplace plus le plan parallèlement à lui-même mais le fait tourner, montrant moultes ellipses et même une parabole en visant bien :

sujets du bac S

Bac S Réunion 2005

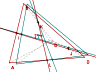
L’un des exercices de ce sujet étrange portait sur un tétraèdre orthocentrique, alors en voici un :

Bac S Pondichery 2008

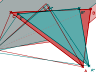
Cette fois-ci c’est le tétraèdre équifacial qui est à l’honneur. Tout d’abord, on demandait de montrer que dans tout tétraèdre, les médianes (droites joignant les milieux de deux arêtes opposées) sont concourantes. La démonstration basée sur l’associativité des barycentres, ne nécéssite pas de « voir » la figure. On constate la difficulté de dessiner des droites en anaglyphes. Ce phénomène est dû à la profondeur de champ trop grande donc irréelle :

Les deux questions suivantes portent sur un tétraèdre équifacial. Dans celle-ci on demandait de montrer que les médianes sont perpendiculaires entre elles :

Puis dans celle-ci que les médianes sont perpendiculaires aux côtés (dans un tétraèdre équifacial) :

S Amérique du Sud Novembre 2004

Juste un exemple pour montrer la puissance d’Euler Math Toolbox pour représenter le volume obtenu en faisant tourner la représentation graphique d’une fonction autour de l’axe des abscisses. Ici il s’agit du volume obtenu par rotation de la fonction définie sur $\left[ 1 ; e \right]$ par $x \mapsto 1-ln(x)$ :

Le fichier Euler pour créer ceci est particulièrement facile à créer ; il s’agit en l’occurence de la première ligne du fichier (téléchargeable ci-dessous [1]) :

>plot3d("1-log(x)",xmin=1,xmax=%e,rotate=1,frame=0,hue=1,anaglyph=1,user=1);

>plot3d("1-log(round(x,1))",xmin=1,xmax=%e,rotate=1,frame=0,hue=1,anaglyph=1,user=1);

>

Si on enlève « frame=0 », on obtient un pavé autour du volume. Le mieux sous Euler est d’ajouter « user=1 » pour faire tourner le volume à l’aide des flèches du pavé.

On peut aussi remplacer « 1-log(x) » [2] par « 1-log(round(x,1)) » (comme ça a été fait pour la deuxième ligne du fichier ci-dessus) pour remplacer la fonction par son arrondi à une décimale près et obtenir l’approximation suivante du volume par une réunion de cylindres :

Alors, si la hauteur de chaque cylindre est $dx$ et le rayon de chacun $1-ln(x)$ alors le volume de chaque cylindre est $\pi\left(1-ln(x)\right)^2dx$ et ainsi, le volume total est

$\displaystyle\int_1^e \pi\left(1-ln(x)\right)^2dx=\pi\int_0^e\left(1-ln(x)\right)^2dx$,

formule qui était rappelée dans l’énoncé du bac.

Souvent les élèves de terminale S se plaignent de ne pas bien « voir » dans l’espace (ce qui est inutile dans cette classe puisque la géométrie dans l’espace y est uniquement analytique). Puissent ces figures les y aider...

Remarque : En téléchargeant les figures, et en les ouvrant avec CarMetal, on peut modifier le paramètre « e » qui est caché en haut à gauche : L’agrandir si l’image est trop double, et le diminuer si elle est trop plate.