Le système dynamique
Le système de Michel Hénon est une suite de points du plan définie par $M(x_n,y_n)\mapsto M’(x_{n+1},y_{n+1})$ où
$\left\{\begin{array}{rlc}x_{n+1}&=&1+y_n-a\,x_n^2 \\ y_{n+1}&=&b\,x_n \end{array} \right.$. Selon les valeurs de a et b, la suite de points peut
– converger :$\lim_{n\rightarrow \infty}M_n = A$
– avoir un attracteur de période 2 : $\lim_{p \rightarrow \infty}M_{2p}=A$ et $\lim_{p \rightarrow \infty}M_{2p+1}=B$ où $A \neq B$
– avoir un attracteur de période $n \in \mathbb{N}$
– diverger : les coordonnées de $M_n$ tendent vers $\infty$, ou la suite est chaotique sur le plan
– avoir un attracteur étrange
Période 1
Un point fixe existe lorsque l’équation $M_{n+1}=M_n$ (en réalité, un système) a une solution dont les deux coordonnées sont réelles. En remplaçant $y$ par $b\,x$ dans $x=1+y-a\, x^2$ on obtient $x=1+b\,x-a\,x^2$, équation du second degré dont le discriminant $\Delta=4a+(1-b)^2$ n’est positif que si le point $A(a,b)$ est à droite de la parabole d’équation $4a+(1-b)^2=0$ dans le plan des (a,b).
Si on déplace le point rouge à gauche de la parabole, le système n’a pas de limite (en fait, il tend vers l’infini). Si on le met à droite de la parabole verte, le système a deux points fixes (les abscisses sont les solutions de l’équation ci-dessus) mais un seul des deux est attractif, et se voit comme limite de la suite $M_n$. Si on déplace le point rouge trop à droite de la parabole verte, le point fixe n’est plus limite de la suite : Il cesse d’être attractif, et se scinde en deux :
Période 2
Un point d’une période 2 se trouve en cherchant deux nombres $x$ et $y$ tels que la transformation de Hénon appliquée à $(1+y-ax^2,bx)$ donne $(x,y)$ :
$1+bx-a\,(1+y-a\,x^2)^2=x$
et
$b(1+bx-a\,x^2)=y$
Ce système se résout en remplaçant le $y$ de la première équation par $b(1+bx-a\,x^2)$ de la deuxième. L’équation étant de degré 4 en $x$, possède 4 solutions, mais les deux points fixes de tout-à-l’heure en font partie. En simplifiant l’équation par celle de la période 1 [1] on obtient une équation du second degré en $x$, ce qui donne bien deux points :
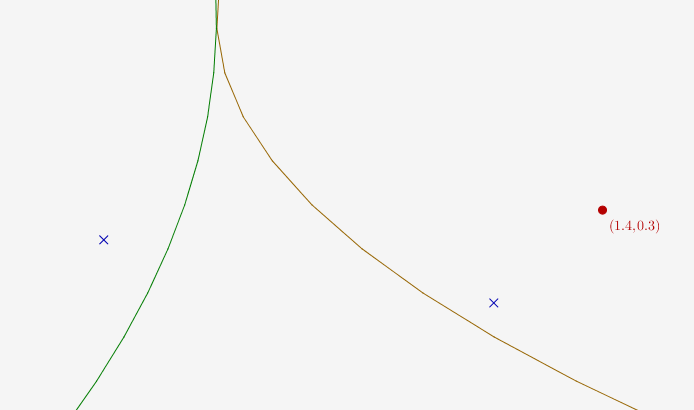
Le discriminant de l’équation précédente est $4a-3(1-b)^2$, équation de la parabole marron. Si on bouge le point à gauche de la parabole marron, les deux points de la période (en bleu) collisionnent et se confondent en le point fixe (en vert lorsqu’il est attractif). Le passage dans l’autre sens (lorsque le point fixe cesse d’âtre attractif et est remplacé par la période 2) s’appelle bifurcation de dédoublement de période. La parabole marron représente donc la zone où il y a un dédoublement de période de 1 vers 2, et le diagramme formé par les deux paraboles (dans le plan des (a,b) qui est ici superposé à celui des (x,y)) est un diagramme de bifurcation. Dans la suite, on va le compléter un peu, mais la structure du diagramme de bifurcation du système de Hénon est un sujet d’actives recherches...
Période 3
La recherche de points de période 3 est nettement plus compliquée mais elle a été faite par Hitzl et Zele en 1985 [2] et la parabole bleue a pour équation $4a=7+10b+7b^2$ :
On constate que la valeur classique (a=1,4 et b=0,3) est à gauche de la parabole bleue, et donc que l’attracteur de Hénon ne possède pas de période 3.
Pour voir la période 3, il faut qu’elle soit attractive et donc le point doit être légèrement à droite de la parabole bleue ; voir plus bas si ce n’est pas le cas.
Période 4
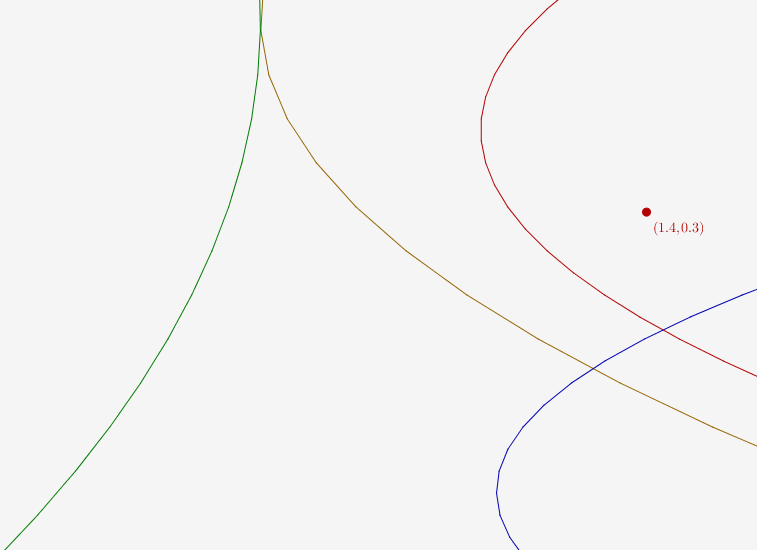
En fait, lorsque le point rouge s’éloigne trop de la parabole marron, les deux points de la période 2 cessent d’être attractifs, et il apparaît par dédoublement de période, une période 4 (quand le point rouge est à droite de la parabole rouge) :
Période 6
De même lorsque le point rouge s’éloigne trop de la parabole bleue vers la droite, bien que la période 3 existe toujours, on ne la voit plus car elle a cessé d’attirer la suite : Elle s’est transformée en une période 6 (par dédoublement de période). Mais la courbe séparatrice n’est plus une parabole (c’est une sextique et elle est représentée en cyan ci-dessous) :
De même, la période 5 n’est pas traitée ici car la courbe n’a pas d’expression analytique connue ; elle possède un point de rebroussement.
Un CarScript
Pour dessiner un nuage de 1000 points qui soit dynamique, il suffit de faire tourner le CarScript suivant :
m=Point("M",1.4,0.3);SetThickness(m,"thick");SetShowName(m,false);
a=Point(0.1,0.2);SetHide(a,true);
for (n=0; n<200; n++){
b=Point("y_a+1-x_m*x_a*x_a","y_m*x_a");
SetShowName(b,false);
SetPointType(b,"point");
a=b;
}Comme les coordonnées de b sont calculées à partir de celles de a et de m (le point de contrôle), tout le nuage dépend de M : Il est dynamique.
Voici donc le nuage des 1000 premiers itérés d’un point par le système de Hénon, où le mouvement du point rouge à la souris montre de façon dynamique ce qui est décrit ci-dessus, et bien d’autres choses. Comme la théorie predit que le système est instable si $\left|b\right|>1$, le point de contrôle a été assigné à ne pas dépasser les lignes pointillées :
Nouveauté 2014 : La figure au format DGPad, manipulable en ligne :
La zone $b \simeq -1$ est particulièrement conseillée.
Pour ce qui est des autres zones (périodes 5, 8 par exemple) le schéma est plus complexe. La forme typique de ces zones est formée de trois courbes comme celles-ci :
La zone comprise entre ces courbes ressemblant à une hirondelle, les zones correspondant à des points de période 5, 7, 8, 9 etc. s’appellent des hirondelles de Milnor. On peut les voir dans cette applet où la forme dissymétrique de certaines hirondelles les fait appeler « crevettes » par l’auteur.
La figure ci-dessus se trouve dans le diaporama fractales des diaporamas des utilisteurs du site de CarMetal. N’en valait-elle pas la peine ?






Commentaires