Corrigé de l’exercice 1 (à prise d’initiative) du bac S 2015

lundi 22 juin 2015
par  Alain BUSSER

Le sujet porte une question à la fin de l’exercice 1, disant que

Dans un des magasins de cette chaîne, sur 200 clients privilégiés, 6 ont reçu un bon d’achat d’une valeur supérieure ou égale à 30€.
Le directeur du magasin considéré estime que ce nombre est insuffisant et doute de la répartition au hasard des bons d’achats dans les différents magasins de la chaîne.
Ses doutes sont-ils justifiés ?

Il s’agit d’un exercice à prise d’initiative puisque rien ne laisse deviner quel outil mathématique peut servir à répondre. Seuls deux indices sont disponibles :

  • Le cours (enfin pour les élèves l’ayant appris !) en particulier celui sur l’aide à la prise de décisions [1] ;
  • La phrase qui est juste au-dessus de cette question, et qui, après avoir demandé de « montrer qu’une valeur approchée à 10-3 près de la probabilité d’avoir un bon d’achat d’une valeur supérieure ou égale à 30 euros vaut 0,057 », disait, en caractères gras, que « pour la question suivante, on utilise cette valeur ».

OK, me dis-je alors, je vais répondre à la question à l’aide d’un intervalle de fluctuation, vu que d’une part je suis censé utiliser les 0,057 (probabilité de succès) de la question précédente, d’autre part, comme je connais le cours de maths, je me souviens de ce que la prise de décision peut être argumentée par l’utilisation d’un intervalle de fluctuation...

Asymptotique ou pas ?

Après tout, puisqu’il s’agit d’un exercice à prise d’initiative, c’est à moi de choisir entre un intervalle de fluctuation (c’est-à-dire utiliser une loi binomiale) et un intervalle de fluctuation asymptotique (basé sur l’approximation normale de la fréquence empirique). Alors, si cet exercice est bien fait, la réponse devrait être la même que l’on prenne l’un ou l’autre. Vérifions, en calculant les deux !

I/ Version intervalle de fluctuation

Avec l’outil en ligne [2], on a juste à entrer les données de l’énoncé et on a le corrigé :

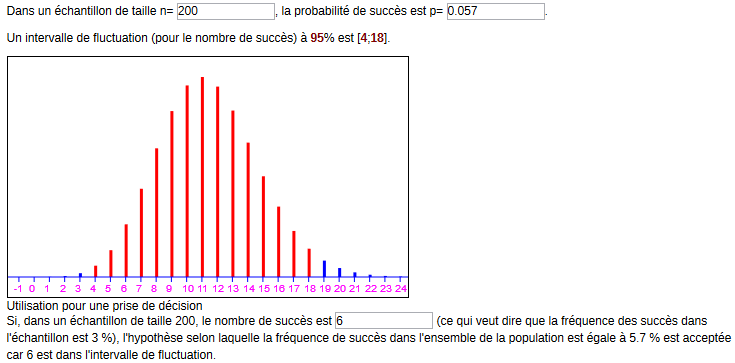
Très bien, il ne reste plus aux candidats, qu’à copier-coller la phrase du bas et hop, la question est finie à part de petites modifications :

Un intervalle de fluctuation (pour le nombre de tickets gagnants) à 95% est [4 ;18]. Si, dans un échantillon de taille 200, le nombre de succès est 6 (ce qui veut dire que la fréquence des succès dans l’échantillon est 3 %), l’hypothèse selon laquelle la fréquence de succès dans l’ensemble de la population est égale à 5,7 % est acceptée car 6 est dans l’intervalle de fluctuation.

Sauf que, les calculatrices des élèves n’étant pas encore dotées de ce petit logiciel libre très fun et très coloré (et très utile !), il faut quand même avoir appris la phrase auparavant, et avoir appris au passage qu’en général on choisit 95% pour les intervalles de fluctuation. Mais au fait pourquoi ? Tiens je ne m’étais pas posé la question. Et si, comme ça, pour voir, on se prenait un intervalle à 90% ? Allez soyons fous ! L’outil précité est facile à utiliser, il y a un cadre en bas où est écrit 0.95, on enlève le 5 et on apprend que l’intervalle est devenu [5 ;17] qui, là encore, contient 6 : La conclusion reste la même, à savoir que non, ses doutes ne sont pas justifiés. Bien, revenons à cette histoire de rédaction : Ou bien on a pensé à programmer la calculatrice en 1re S pour qu’elle calcule l’intervalle de fluctuation à 95% [3], et dans ce cas on rédige à peu près ce qui est au-dessus, ou bien on a manqué de prévision [4] et alors il faut le reprogrammer cet algorithme. Ou pas...

Après tout il suffit de calculer les valeurs de la fonction de répartition de la loi binomiale de paramètres 200 et 0,057 jusqu’à ce qu’on dépasse 0,025 (parce que 5% équirépartis autant que possible entre les bords gauche et droit de la cloche, ça fait 2,5%). Coup de chance, l’auteur de l’outil précédent a eu la gentillesse de programmer aussi un calculateur de probabilités binomiales [5] dans lequel il suffit d’entrer 200, 0,057 et les entiers successifs jusqu’à ce que la probabilité affichée dépasse 0,025. On a vite fait de trouver 5, mais comme dans ce cas on a dépassé 0,025 on prend 4, qui avait été affiché tout-à-l’heure.

Mais, allez-vous me dire, « il est bien joli votre outil de calcul de probabilités binomiales (merci !), mais vu qu’il n’est pas sur notre calculatrice, il ne nous sert à rien ». Ce à quoi je répondrai que si votre calculatrice ne vous permet pas de calculer ces probabilités avec une fonction du genre binomFRép, vous pouvez la jeter [6]...

Maintenant, une initiative imprévue surgit soudain du brouillard comme un taxi dans un film de Hitchcock : Essayer comme ça pour voir avec 6 :

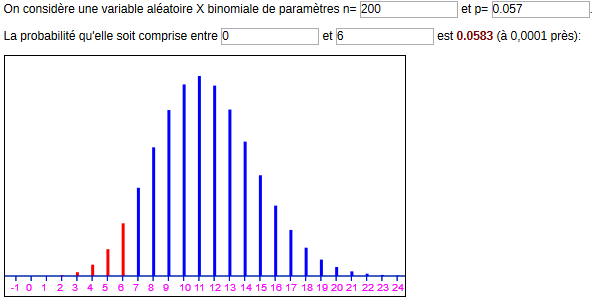
Avec ça, plus besoin de se poser de questions sur les 90% ou 95%, et hop on a un corrigé encore plus court que le précédent :

Le directeur trouve les 6 tickets gagnants anormalement peu nombreux par rapport à la moyenne de 11,4. Or la probabilité que le nombre de tickets gagnants soit au plus 6, pour une loi binomiale de paramètres 200 et 0,057, n’est pas suffisamment petite (0,058) pour justifier l’inquiétude du directeur.

Oui, mais, initiative pour initiative, quand on en arrive à décider seul de la taille d’un nombre, on peut tout aussi bien faire le choix contraire :

Le directeur trouve les 6 tickets gagnants anormalement peu nombreux par rapport à la moyenne de 11,4. Or la probabilité que le nombre de tickets gagnants soit au plus 6, pour une loi binomiale de paramètres 200 et 0,057, est suffisamment petite (0,058 seulement) pour justifier l’inquiétude du directeur.

Ah ces maths modernes ! Deux réponses contradictoires entre elles sont tout aussi justes l’une que l’autre. On commence à le trouver rigolo finalement cet exercice ! Au fait, puisqu’on est en train de se demander s’il convient ou non, de s’étonner de la survenue d’un évènement rare, on peut continuer sur cette voie (allez encore une initiative) : Finalement, un intervalle de fluctuation unilatéral est plus approprié pour ce problème ! Pour éviter la surenchère d’initiatives, on va se contenter de le prendre à 95% ; et justement, dans ce cas, la probabilité que le nombre de tickets gagnants soit inférieure ou égale à 6 est, on l’a vu, de plus de 0,05 ; donc l’intervalle de fluctuation pour un test unilatéral est [5 ;200] qui, là encore, est de nature à rassurer ce pauvre directeur.

II/ Version intervalle de fluctuation asymptotique

Un bon élève de terminale S, qui a bien écouté son prof toute l’année [7], devrait avoir pour réflexe de calculer un intervalle de fluctuation asymptotique, en approchant la fréquence de tickets gagnants par une variable aléatoire normale, d’espérance 0,057 et d’écart-type √(0,057×0,943/200) soit environ 0,0164. Cette approximation est justifiée si

  • 200 est un grand nombre (supérieur à une trentaine) ce qui est le cas ;
  • 200×0,057 est supérieur à 5, c’est le cas ici puisque le produit vaut 11,4 ;
  • 200×0,943 est aussi supérieur à 5 ; c’est encore plus le cas puisque le produit vaut 188,6.

Alors on peut refaire l’exercice avec le calculateur en ligne, tatatsoin, d’intervalles de fluctuation asymptotique [8] :

« M’sieur, M’sieur ! On vous aime bien, mais, comment dire ... Fait une heure qu’on essaye de vous expliquer que vot’logiciel à la c... (merci !) y’en a paaaaas sur not’calculatrice que c’est le seul truc qu’on a le droit d’utiliser au bac. Faut vous le dire dans quelle langue ? »

Vous affolez pas (et puis, pas sur la tête, j’ai plus trop de cheveux dessus, ça fait mal). Vous n’avez pas de logiciel qui vous fait tout le boulot ? Et bien, vous le faites, le boulot !

  1. Pour calculer l’espérance, voir en 1re, on fait n×p=11,4 et j’ai déjà dit, pas sur la tête !
  2. Pour l’écart-type c’est un peu plus dur, mais ça été vu en 1e : √(p×q/n) ; et comme q=1-p=1-0,057=0,943 même avec votre calculatrice qui n’est même pas sous licence Gnu/GPL on peut faire le calcul. Pour toute réclamation adressez-vous à votre prof de 1e est c’est sur sa tête à lui qu’il faut taper, pas sur la mienne...
  3. On trouve, normalement (!), 0,0164, que d’après le cours de Terminale, on doit multiplier par 1,96 pour avoir la demi-largeur de l’intervalle de fluctuation, on trouve 0,032 qu’il suffit de soustraire et additionner à 11,4 pour avoir l’intervalle de fluctuation asymptotique, et j’ai dit pas sur la tête !

Comme ça vous avez l’intervalle de fluctuation asymptotique qui était probablement l’attendu : [0,0025 ;0,089] ; comme les 0,03 constatés par le directeur sont dans cet intervalle, ses doutes ne sont pas plus justifiés que s’il avait pris l’intervalle de 1re. Sauf que là, si on prend un intervalle à 90% (ce que l’énoncé n’interdisait pas formellement, ah ces exercices à prise d’initiative !) les 0,03 sont pile à la limite inférieure de l’intervalle et on a un peu du mal à répondre...

L’avis de la Faculté

Coup de chance, je reçois la visite d’un ancien élève [9] qui est actuellement étudiant en médecine. Il me dit « attends, en médecine on ne se complique pas la vie comme ça, on calcule un intervalle de confiance, la calculatrice le fait directement ». Renseignement pris auprès d’un praticien, j’ai eu ceci comme réponse :

« a priori la réponse est relativement simple : si l’intervalle de confiance à 95% autour de la valeur 0.057 inclut la valeur de 0.03 (3% des privilégiés), le directeur se méprend. Par exemple 0.057 +/- 0.03, si l’IC est de 0.06. Dans ce cas, la Loi normale, robuste, montre que les clients privilégiés ne le sont pas plus que d’autres non privilégiés. Et même moins privilégiés (le directeur aurait raison) si l’IC est strictement < à 0.048. Mais on peut choisir d’autres IC, à 90% par exemple, ou à 99% ; Donc tout dépend de ce que l’on se fixe comme IC dès le départ. »

Intéressant : Lorsqu’un prof de maths qui a mal à la tête se permet l’outrecuidance d’utiliser un intervalle de confiance à la place d’un intervalle de fluctuation, il attire instantanément sur lui, l’ire des statisticiens qui le traitent d’amateur en le domaine (ce en quoi ils ont d’ailleurs parfaitement raison). Alors que la profession médicale, grande consommatrice de statistiques, ne s’encombre guère de ce genre de complications avec pour seule conséquence du point de vue des statisticiens, que « vous voyez qu’il faut enseigner la statistique inférentielle, elle est utilisée même en médecine ». Le prof de maths aimerait donc que les médecins pratiquant au quotidien la statistique inférentielle, lui prescrivent du paracetamol pour l’aider à oublier les coups sur la tête émanant des statisticiens en colère...

La calculatrice possédant une fonction de calcul d’intervalles de confiance, on peut calculer celui-là en quelques secondes, et on trouve que l’intervalle à 95% est [0,006 ;0,054]. Coup de théatre : Il ne contient pas les 0,057 voulus...

Cette expérience a le mérite de montrer que l’intervalle de confiance produit par la calculatrice n’est pas celui qui est enseigné en terminale S mais celui des sections technologiques. Celui enseigné en terminale S est le même que celui enseigné en 2e, et celui-ci est [0 ; 0,107] qui, lui, contient les 0,057...

Ainsi, si le directeur était médecin [10], il estimerait avoir quand même raison de se sentir lésé dans la distribution des tickets gagnants. Mais de pas beaucoup, et seulement si l’intervalle est à 95%...

En BTS

Un problème soulevé par ce problème, on l’a vu plus haut, est que l’approximation normale est à peine justifiée parce que p=0,057 est tout de même assez petit (on a vu en 2de que p est supposé compris entre 0,2 et 0,8 pour calculer les intervalles de confiance et de fluctuation ; on est en droit de prendre l’initiative de réclamer une certaine cohérence dans les programmes...). Or, pour p petit, une approximation par une variable de Poisson de paramètre 11,4 est peut-être plus appropriée. Voyons ce que ça donne ici :

Version unilatérale :

L’auteur des logiciels libres cités ci-dessus semble avoir quelque peu anticipé la question puisqu’il y a un outil approprié. Il donne ceci :

Avec une probabilité qu’il y ait aussi peu de tickets gagnants, égale à 0,064 environ, les conclusions sont les mêmes que tout-à-l’heure, à savoir que si on veut être prudent et minimiser le risque, on peut attribuer ce nombre 6 à la seule fluctuation d’échantillonnage ; sinon on trouve que 0,064 est finalement assez grand pour avoir des doutes, et là encore l’exercice laissait trop d’initiative pour avoir une réponse certaine [11].

L’intervalle de fluctuation unilatéral à 95% est [6 ;200] qui contient (tout juste) les 6 tickets gagnants. Mais c’est un intervalle à 97% en fait.

Version bilatérale

Le diagramme en bâtons de la loi de Poisson ressemblant à une courbe en cloche, on peut aussi, pour comparaison, calculer un intervalle de fluctuation bilatéral à 95% ; on trouve, avec l’outil ci-dessus ou la calculatrice (fonction PoissonFRép), l’intervalle [5 ;18] :

Comme cet intervalle contient 6, le directeur n’a pas de raisons de douter... sauf que s’il avait reçu trop de tickets gagnants il ne se serait pas plaint, et que le choix d’un intervalle bilatéral (que ce soit Poisson, binomial ou normal) n’est pas approprié à ce problème...

Conclusion

L’époque où, pour avoir une bonne note en maths, il fallait trouver la bonne réponse, est bien révolue, avec ces exercices où il n’y pas de « bonne » réponse unique (il est où mon paracétamol ?)


[1] Le programme de Terminale dit que « La problématique de prise de décision, déjà rencontrée, est travaillée à nouveau avec l’intervalle de fluctuation asymptotique » ; ce qui nous donne une piste : Le programme de Première S, lequel, sur ce sujet, parle juste d’« exploiter l’intervalle de fluctuation à un seuil donné, déterminé à l’aide de la loi binomiale, pour rejeter ou non une hypothèse sur une proportion ». il y a donc deux initiatives à prendre : Le choix du seuil, et le choix entre intervalle de fluctuation et intervalle de fluctuation asymptotique.

[2] Consulté en moyenne deux fois par jour durant le dernier trimestre.

[3] L’agorithme n’est pas très difficile et c’est une bonne occasion de voir l’utilité des boucles « until ».

[4] Ou on a vidé la mémoire de la calculatrice, à cause de piles vides ou d’un vicieux « mode examen », on ne rigole pas, ça existe.

[5] Lu en moyenne 10 fois par jour durant le mois de juin.

[6] Dans une ressourcerie SVP, il y a plein de choses à recycler dedans. Ce n’est pas parce qu’on est énervé qu’on ne doit pas être écolo...

[7] Est-ce le cas de mes élèves ? J’en doute parfois...

[8] Utilisé en moyenne 20 fois par jour depuis le début du bac...

[9] Bac C, 20 en maths au BTS...

[10] S’il était médecin, peut-être ne voudrait-il pas pousser à la cosommation...

[11] Dans l’exercice 4, on demandait s’il est vrai que « l’inclinaison de la piste est presque deux fois plus grande en B qu’en C ». Presque n’importe quelle réponse peut être considérée comme... presque bonne : On est en pleine logique floue ; en ce qui concerne le respect du programme, on est surtout en plein flou...


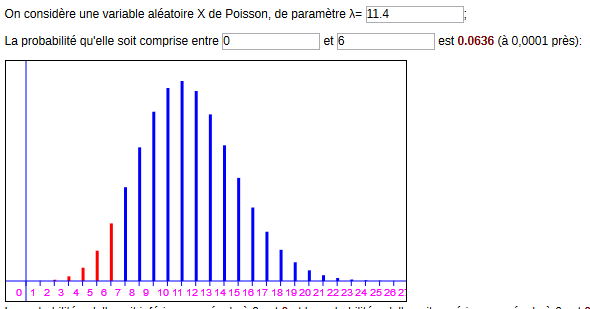
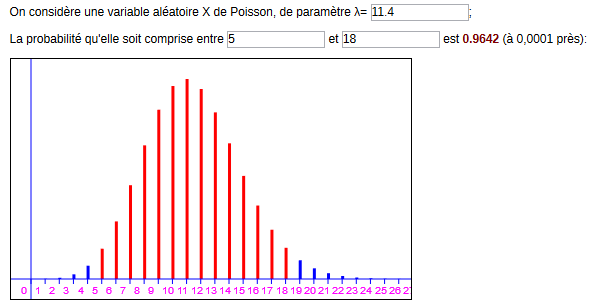
Commentaires