


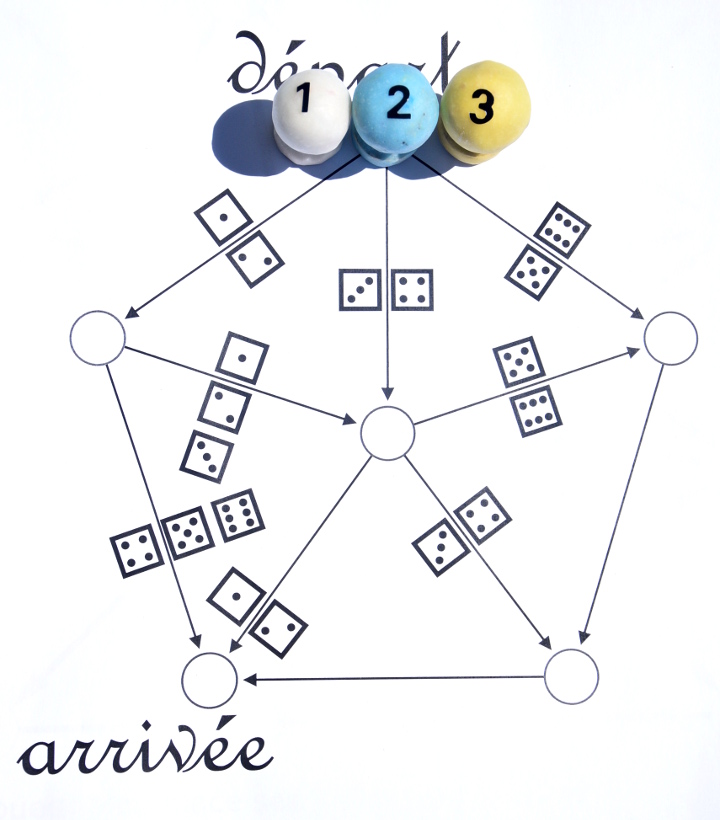
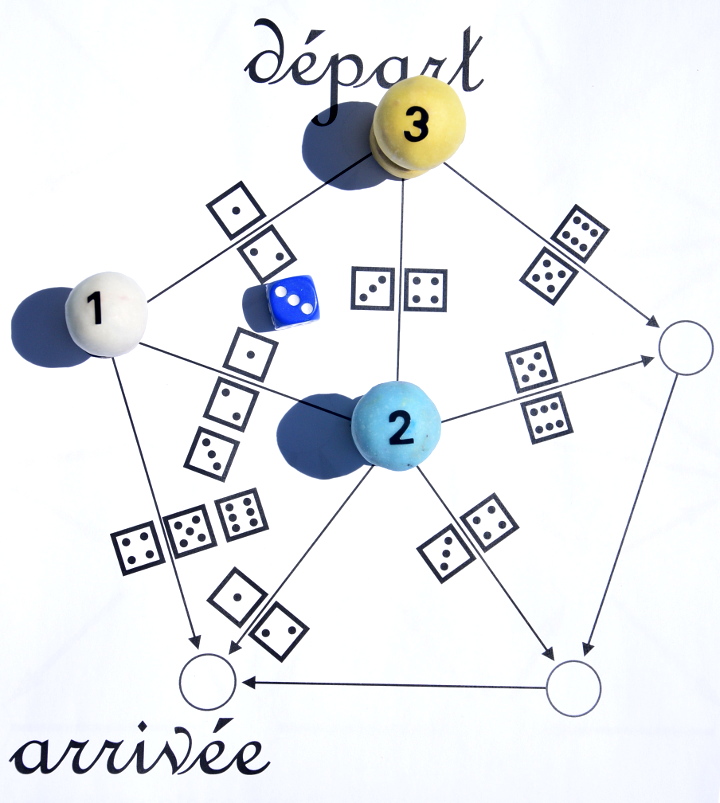
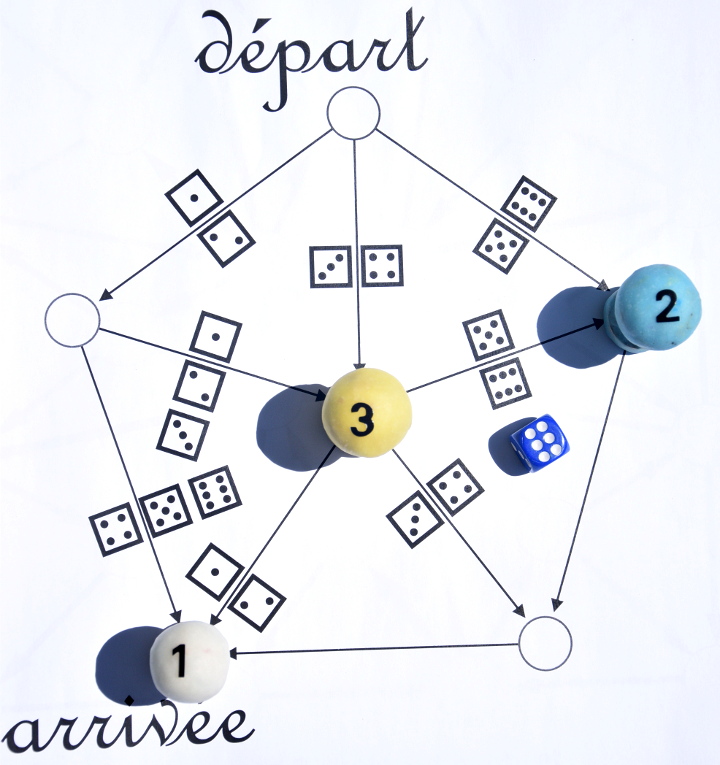
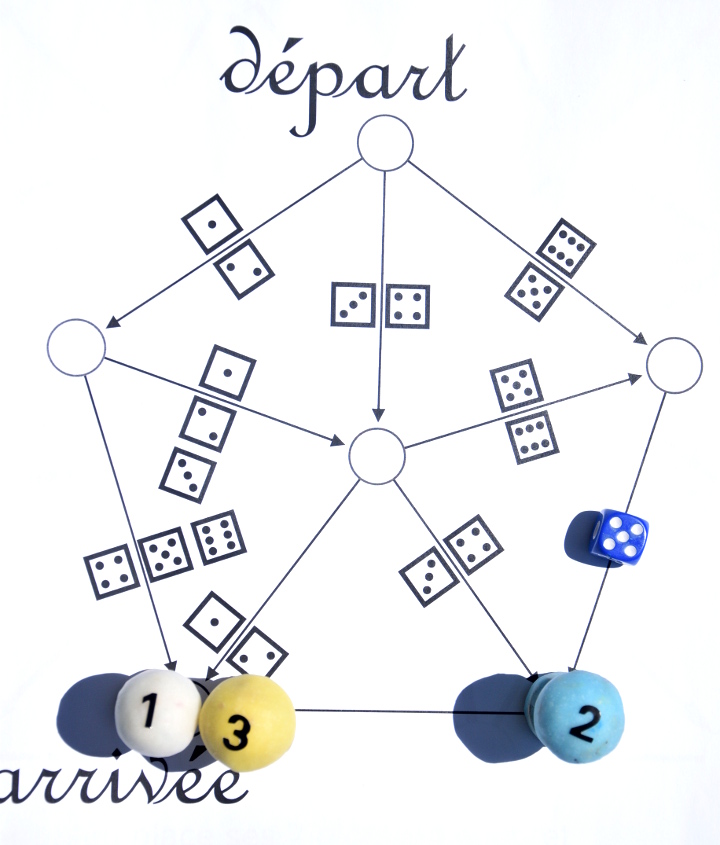
Pour les algorithmes (parcours séquentiel, tri) a été préparé ce jeu de cartes numérotées :

Parcours séquentiel d’un tableau
Longueur
Cet algorithme est hors programme. Chaque élève dispose d’un jeu de cartes numérotées. Il est d’abord demandé de compter les cartes. Ensuite on compare le nombre de cartes (le résultat du comptage) avec le temps que ça a pris de compter. On constate que ce temps (« le coût ») dépend linéairement du nombre de cartes.
Voici la version Python :
def longueur(L: list) -> int
compteur = 0
for elt in L:
compteur += 1
return compteurMais Python possède une fonction len (comme « length ») qui fait ce comptage.
Appartenance
Le programme parle d’
écrire un algorithme de recherche d’une occurence sur des valeurs de type quelconque.
Là encore, l’activité commence par la distribution d’un jeu de cartes mélangé (non trié). Les cartes sont distribuées par tas de 8. Puis on demande de voir si la carte 13 fait partie du jeu. Mais de verbaliser chaque étape de la recherche. Ce qui donne des retours de ce genre :
On prend les cartes une par une, on les regarde et on les compare avec 13. On s’arrête lorsqu’on a trouvé 13.
Les élèves comprennent alors qu’il a fallu regarder 8 cartes (parce qu’aucune carte ne porte le nombre 13, le jeu a été préparé comme ça). Voici la version Python :
def contient(L:list,elt) -> bool:
for x in L:
if x==elt:
return True
return FalseMais Python possède une opération infixe in qui représente l’appartenance ∈ :
def contient(L:list,elt) -> bool:
return elt in LLe programme dit aussi que
On montre que le coût est linéaire.
Si on complète la phrase par « dans le pire cas » c’est facile puisque le pire cas est celui où l’élément n’est pas dans la liste, comme 13 ci-dessus. Alors pour vérifier que l’élément ne figure pas dans une liste de longueur n, on doit effectuer n comparaisons cqfd.
Le fait que les élèves verbalisent, amène certains d’entre eux à imaginer spontanément que le résultat ci-dessus est trop pessimiste si la liste est triée (ce n’est pas le cas ici). Il leur a été répondu que ce cas sera étudié ultérieurement (recherche dichotomique, plus bas).
Si le coût est linéaire dans le pire cas, il est constant dans le meilleur cas (une seule vérification si l’élément se trouve en première position). La théorie des probabilités permet de montrer que le coût est linéaire en moyenne : si les positions d’une carte sont équiprobables, l’élément cherché se trouve en moyenne au milieu de la liste. Il faut alors effectuer en moyenne n/2 comparaisons ce qui est bien linéaire. Ces remarques mènent à ne regarder que le pire cas par la suite.
Minimum

Citons encore le programme :
Écrire un algorithme de recherche d’un extrémum [...]
On montre que le coût est linéaire.
Le début du jeu reste le même : on distribue à chaque élève 8 cartes portant des entiers, chaque paquet de 8 cartes étant mélangé. On demande alors aux élèves de trouver la plus petite (portant le plus petit numéro) carte du jeu, toujours en verbalisant chaque étape. On arrive alors à entendre des choses comme
On extrait la première carte du jeu, puis on regarde les cartes l’une après l’autre. Chaque fois qu’on trouve une carte plus petite que la carte extraite, on l’échange avec la carte extraite.
Comme on regarde l’une après l’autre toutes les cartes du jeu, le coût est encore une fois linéaire.
Voici la version Python, qui a été l’occasion d’introduire la notion de post-condition (l’avant-dernière ligne, commençant par assert) :
def minimum(L:list) -> float:
m = float("inf")
for elt in L:
if m>elt:
m=elt
assert all([m<=x for x in L])
return mCette postcondition vérifie que m≤x pour tout x de la liste, c’est-à-dire que m est bien le minimum de la liste. Si ce n’était pas le cas, Python s’arrêterait avec un message d’erreur.
Pour être certain de la correction de cet algorithme, on s’assure qu’au début m est plus grand que tous les éléments de la liste, ce qui est certain si au début, m=∞.
La fonction min de Python implémente cet algorithme. On pouvait donc aussi faire
def minimum(liste:list) -> float:
return min(liste)mais cela ne décrirait évidemment pas l’algorithme.
Remarque : L’algorithme ne nécessite pas que les éléments de la liste soient des nombres. Il suffit qu’il y ait une relation d’ordre sur ces éléments. Par exemple, avec une liste de mots (chaînes de caractères de type str) l’algorithme renvoie le mot qui vient avant les autres dans l’ordre alphabétique.
Maximum

L’activité est similaire à celle sur le minimum, à ceci près qu’une fois les paquets de cartes fournis aux élèves, on leur demande d’extraire la plus grande carte.
Mais la similitude avec l’activité précédente a mené à une autre forme d’activité : un devoir maison, les élèves étant chargés d’écrire un script Python donnant le plus grand élément d’une liste Python. Voici le corrigé :
def maximum(L:list) -> float:
m = L[0]
for elt in L:
if m<elt:
m=elt
return mRemarque : Plusieurs élèves ont cherché une erreur dans leur scipt qui n’en contenait pas, simplement parce qu’en exécutant le script, ils ne voyaient rien se passer.
Il leur a été rappelé que pour voir quelque chose, il fallait tester la fonction sur un (ou plusieurs) exemple. Par exemple
>>> maximum([2,3,2,8,5])
8Python possède une fonction max qui évite d’avoir à implémenter l’algorithme.
L’algorithme ci-dessus est lui aussi de coût linéaire.
Somme
Toujours avec un paquet de 8 cartes (mélangées), il est maintenant demandé aux élèves d’additionner toutes les cartes (en fait, le nombres qui sont dessus). La verbalisation vient moins vite que pour les activités précédentes :
On additionne les deux premières cartes.
On additionne le résultat à la troisième carte.
On additionne le résultat à la quatrième carte.
etc.
Traduit en Python, cet algorithme fait intervenir une variable accumulant les sommes partielles :
def somme(L:list) -> float:
S = 0
for elt in L:
S += elt
return SCet algorithme est également de coût linéaire, puisqu’on regarde toutes les cartes.
Pour montrer qu’il additionne bien les 8 nombres, on introduit une nouvelle notion, celle d’invariant de boucle. Un invariant de boucle est une proposition qui
- est vraie lorsqu’on entre dans la boucle ;
- reste vraie à chaque passage dans la boucle.
Ici on propose comme invariant « au k-ième passage dans la boucle, la variable S est égale à la somme des k premiers élements de la liste ».
- comme la somme de rien est 0, l’invariant est vrai lorsque k=0.
- Si, au k-ième passage, S contient la somme des k premiers éléments de la liste, alors au passage suivant, S contient cette somme additionnée du (k+1)-ième élement. Ce qui est bien la somme des k+1 premiers éléments.
Alors l’invariant est resté vrai jusqu’à la sortie de la boucle, et par conséquent à la fin, S contient la somme de tous les élements de la liste. Ce qui prouve la correction de l’algorithme.
La fonction sum de Python implémente cet algorithme :
def somme(L:list) -> float:
return sum(L)Remarque : L’algorithme n’utilise pas réellement le fait que la liste est une liste de nombres, mais seulement qu’on peut additionner ses éléments. Le même algorithme permet donc également
- de calculer la somme d’une liste de vecteurs
- de calculer la concaténée d’une liste de chaines de caractères, comme le fait la fonction Python join.
Moyenne
On peut donner un paquet de 8 cartes à chaque élève puis demander comment calculer la moyenne des 8 nombres. Mais avec ce qui précède on a directement cette verbalisation :
Pour avoir la moyenne, on divise la somme par 8 car on a vu qu’il y avait 8 cartes.
Ce qui en Python donne cet algorithme :
def moyenne(L:list) -> float:
return somme(L)/len(L)Pour additionner n nombres, on a vu dans l’onglet précédent qu’il fallait effectuer
- n lectures de cartes
- n-1 additions (n si on commence par additionner 0 à la première carte).
Et pour compter les cartes il a fallu effectuer
- n lectures de cartes
- n-1 additions de 1 (n additions si on commence par 0+1=1).
Donc a priori il faut n+n-1+n+n-1=4n-2 (ou 4n) opérations élémentaires pour calculer la moyenne. Mais comme la lecture n’a pas besoin d’être faite deux fois on peut imaginer cette variante de l’algorithme :
def moyenne(L:list) -> float:
S = 0
N = 0
for elt in L:
S += elt
N += 1
return S/NLà il ne faut plus que 3n opérations élémentaires. Les deux algorithmes sont de coût linéaire.
Tris par insertion, par sélection
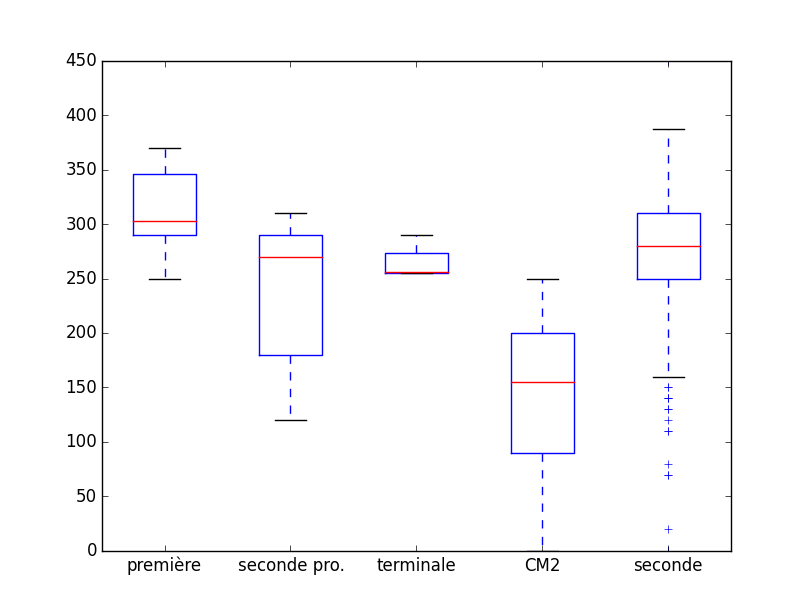
On recommence comme dans les situations précédentes mais, au lieu de mettre les 8 cartes en tas, on les pose l’une à côté de l’autre. Cette fois-ci il s’agit de trier dans l’ordre croissant les cartes, toujours en verbalisant les étapes du tri. Le but est de découvrir quel algorithme de tri est le plus naturel chez les élèves. Statistiquement le tri par sélection est inventé 5 fois plus souvent que le tri par insertion, dans l’échantillon d’élèves de 1re.
Vide
Pour la suite on aura besoin de savoir si une liste est vide (si la liste à trier est vide ça veut dire qu’on a fini). Pour ce faire on va utiliser sa longueur : Une liste vide, c’est une liste de longueur nulle :
def vide(liste:list) -> bool:
return len(liste)==0Sélection
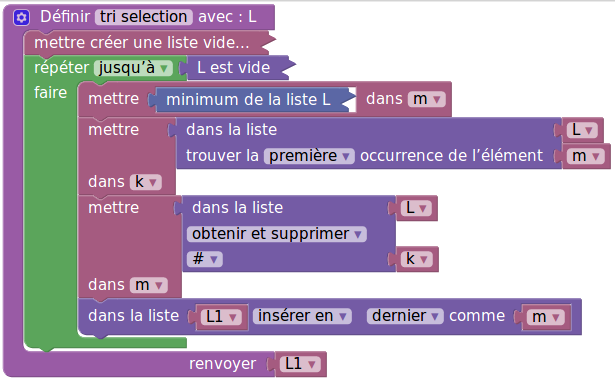
Maintenant qu’on sait trouver le minimum d’une liste (voir plus haut), on peut s’en servir pour effectuer le tri par l’algorithme dit de sélection, consistant à faire ceci :
- on repère la plus petite carte de la liste à trier
- on retire cette carte du jeu
- on la place à la fin de la nouvelle liste
- lorsqu’il ne reste aucune carte dans la liste à trier, on a fini.
On a vu dans l’onglet précédent comment programmer en Python le test de fin. La seconde liste, appelée liste_triée, est initialement vide. Le but du tri est de vider la liste initiale (appelée liste_à_trier) et en même temps remplir la nouvelle liste. Cela avec les étapes décrites ci-dessus :
def tri_selection(liste_à_trier:list) -> list:
liste_triée = []
while not vide(liste_à_trier):
carte = minimum(liste_à_trier)
enlever(liste_à_trier,carte)
ajouter(liste_triée,carte)
return liste_triéeReste à voir comment on fait, en Python, pour enlever la carte :
def enlever(liste:list,elt:float):
liste.remove(elt)et pour l’insérer à la fin du nouveau jeu de cartes :
def ajouter(liste:list,elt:float):
liste.append(elt)Complexité
Pour trier, par cet algorithme, un jeu de n cartes, on effectue n extractions de cartes de la première liste, et n « insertions » dans la seconde liste, soit 2n mouvements de cartes. Mais pour la recherche de minimum, on a vu précédemment que
- on doit effectuer n comparaisons lorsque la première liste est encore pleine ;
- puis n-1 comparaisons après l’extraction d’une carte ;
- puis n-2 comparaisons ;
- puis n-3 comparaisons ;
- etc
soit en tout , n+n-1+n-2+...+2+1=S(n).
Chercher l’expression de S(n) fonction de n n’est pas au programme de NSI, mais il existe des preuves par le dessin, et on peut également faire appel à l’intelligence artificielle de OEIS qui révèle (après soumission des premières valeurs 1, 3, 6, 10, 15) que cette somme est n(n+1)/2 qui est de toute façon majorée par n² (tout du moins si n est entier). Alors on peut prouver cette majoration en modifiant ainsi le raisonnement ci-dessus :
- on doit effectuer n comparaisons lorsque la première liste est encore pleine ;
- puis moins de n comparaisons après l’extraction d’une carte ;
- puis moins de n comparaisons ;
- etc
Et on effectue en tout moins de n×n=n² comparaisons. Ce qui fait en tout n+n+n² opérations élémentaires, soit moins de 3n² (aucun entier ne dépasse son carré) : Le coût de cet algorithme est, au pire, quadratique.
En effet on ne peut pas mieux. Si au départ les cartes sont dans l’ordre décroissant, on doit vraiment effectuer n comparaisons puis n-1 comparaisons et ainsi de suite. Dans ce cas on ne peut donc faire mieux que n(n+1)/2 comparaisons. Or parmi les entiers de 1 à n, la moitié d’entre eux sont plus grands que n/2. Donc leur somme est plus grande que n²/4, et la somme de tous les entiers l’est également. On ne peut donc, dans le pire cas, descendre en-dessous de n²/4.
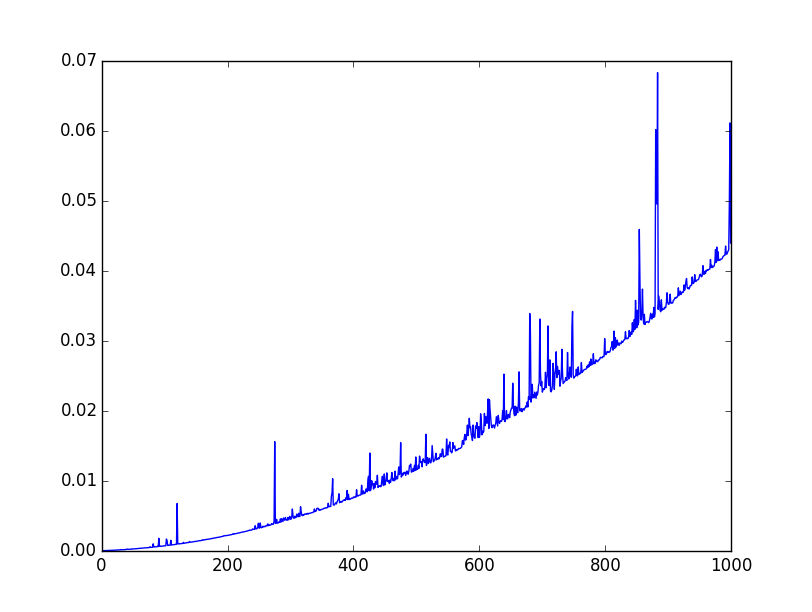
On voit cette tendance sur des mesures effectuées par Python (en abscisse, la taille de la liste ; en ordonnée, le temps que ça a pris pour la trier, en microsecondes) :
Le fait que le coût est quadratique se voit à l’allure parabolique de la « courbe ».
Correction de l’algorithme
Comment prouver que la liste obtenue à la fin est bel et bien triée dans l’ordre croissant ? On peut déjà faire faire la vérification sur plusieurs cas, par Python, avec cette variante :
def tri_selection(liste_à_trier:list) -> list:
liste_triée = []
while not vide(liste_à_trier):
assert liste_triée==sorted(liste_triée)
carte = minimum(liste_à_trier)
enlever(liste_à_trier,carte)
ajouter(liste_triée,carte)
return liste_triéeLa ligne ajoutée est
assert liste_triée==sorted(liste_triée) Elle vérifie que la seconde liste est égale à la version triée (sorted) de celle-ci ; autrement dit, que la liste est triée.
Si, à un quelconque moment de l’exécution du script, la seconde liste n’était pas triée, le script s’arrêterait sur une assertion error. Le fait que ce n’est pas le cas suggère de prendre pour invariant la liste de sortie est triée :
- au départ la seconde liste est vide, donc triée.
- Si elle est triée à l’entrée de la boucle, elle l’est aussi à la sortie, parce qu’entre temps on a ajouté à la fin de la seconde liste, une carte plus grande que toutes celles de la liste. Pourquoi ? Parce que toutes les cartes qui étaient dans la liste à l’entrée de la boucle avaient été précédemment extraites de la liste de départ comme minimum de celle-ci, et étaient donc plus petites que celle qu’on vient d’ajouter.
Terminaison
Pour prouver que le programme se termine au bout d’un temps fini, un variant vient naturellement à l’esprit, c’est la taille de la liste restant à trier. Or celle-ci décroit d’une unité à chaque passage dans la boucle, donc il y a n passages dans la boucle et le programme se termine au bout d’un temps fini.
Insertion

Une autre méthode est en quelque sorte l’inverse de la précédente : on extrait une carte plus facile à trouver que la plus petite (la dernière carte, qu’il est immédiat de trouver) mais on passe plus de temps à l’insérer dans le nouveau jeu de cartes, puisqu’il faut l’insérer (d’où le nom de l’algorithme) au bon endroit dans le nouveau jeu. On fait comme ceci :
- On crée une liste (pas vide, on verra tout-à-l’heure pourquoi) qui sera triée dans l’ordre croissant.
- On prend la dernière carte de la liste de départ.
- On l’insère dans la nouvelle liste, en s’assurant que la nouvelle liste restera triée. Pour cela
- on regarde, une après l’autre, les cartes de la nouvelle liste, jusqu’à ce qu’on trouve une carte plus grande que celle qu’on veut insérer (ça va assez vite car la liste est triée) ;
- on insère la nouvelle carte juste avant la carte qu’on vient de trouver.
- On recommence jusqu’à ce que la liste initiale soit vide : il n’y a plus rien à trier.
En Python cela donne :
def tri_insertion(liste_à_trier:list) -> list:
liste_triée = [float('inf')]
while not vide(liste_à_trier):
carte = liste_à_trier.pop()
ajouter(liste_triée,carte)
liste_triée.pop()
return liste_triéeComme on doit insérer la nouvelle carte juste avant la première carte qui la dépasse dans la liste triée, il faut qu’il y ait dès le départ, une carte plus grande que toutes les cartes de la liste initiale. On ajoute donc provisoirement une carte infinie, devant laquelle seront placées dans l’ordre croissant toutes les autres cartes.
Pour retirer le dernier élément d’une liste, on utilise la fonction pop de Python. Le nom de cette fonction est une onomatopée, le retrait étant similaire à l’action de déboucher une bouteille de champagne. L’élément retiré est la carte qu’on extrait de la liste initiale dans la boucle, et la carte « ∞ » à l’avant-dernière ligne.
Pour ajouter une carte au bon endroit, il faut donc effectuer une boucle :
def ajouter(liste:list,elt:float):
position = 0
for position in range(len(liste)):
if liste[position]>elt:
break
liste.insert(position,elt)L’instruction break a pour effet de quitter le corps de la boucle (dès qu’on a trouvé une carte plus grande que celle à insérer, ce qui signifie qu’on a fait un pas de trop).
Complexité
Pour le tri par sélection, on a vu dans l’onglet précédent que dans le pire cas il faut effectuer autant de comparaisons dans la liste de départ, que celle-ci contient de cartes, puisqu’on ne peut pas savoir d’avance où est la plus petite carte.
Pour le tri par insertion, c’est au contraire la liste en cours de construction qu’il faut parcourir en entier, parce qu’on ne sait pas d’avance où il faut insérer la carte extraite de l’ancienne liste :
- La première carte est à insérer au début de la nouvelle liste, il n’y a pas besoin de comparaison à effectuer pour cela.
- La seconde carte doit être comparée avec la première pour savoir où l’insérer.
- La troisième carte est à comparer avec les deux premières pour savoir où l’insérer.
- etc.
Donc il faut 0+1+2+...+n-1=n(n-1)/2 comparaisons pour constituer la seconde liste (celle qui est renvoyée à la fin). En ajoutant les n extractions de cartes et les n insertions de cartes cela fait encore une fois un nombre d’opérations élémentaires majoré par 3n² : Le coût est encore quadratique dans le pire cas.
Des mesures effectuées avec Python confirment graphiquement ce résultat :
Correction
Python peut également être sollicité pour vérifier que la liste est bien triée à la fin, en comparant la liste à sa version triée fournie par la fonction sorted. Cela se fait en ajoutant cette postcondition :
def tri_insertion(liste_à_trier:list) -> list:
liste_triée = [float('inf')]
while not vide(liste_à_trier):
carte = liste_à_trier.pop()
ajouter(liste_triée,carte)
liste_triée.pop()
assert liste_triée==sorted(liste_triée)
return liste_triéeL’avant dernière ligne (le rajout) prétend que la liste est effectivement triée. Si ce n’était pas le cas, Python s’arrêterait sur un message d’erreur (« assertion error »). Le fait que ça n’arrive pas prouve que, pour la liste précise choisie en entrée, l’algorithme est correct. Comment établir la preuve dans le cas général ?
Voici une petite modification qui apporte quelque chose :
def tri_insertion(liste_à_trier:list) -> list:
liste_triée = [float('inf')]
while not vide(liste_à_trier):
assert liste_triée==sorted(liste_triée)
carte = liste_à_trier.pop()
ajouter(liste_triée,carte)
liste_triée.pop()
return liste_triéeOn a juste déplacé l’assertion, en en faisant une pré-assertion pour la boucle. L’absence de message d’erreur montre que, dans le cas particulier de la liste choisie en entrée, la seconde liste n’est pas triée seulement à la fin, mais elle le reste en permanence. Cela signifie que l’assertion serait, en réalté, un invariant de boucle :
- Une liste vide est triée (on ne tient pas compte de la dernière carte qu’on enlèvera à la fin). L’invariant est donc vrai dès le début.
- Chaque fois qu’on ajoute une carte dans la nouvelle liste, on la place juste là où il faut pour que la liste reste triée.
On a donc un invariant : « la nouvelle liste est triée tout au long de son existence ». Et en prouvant que c’est un invariant, on prouve que l’algorithme fait bel et bien un algorithme de tri : si la liste est tout le temps triée, elle l’est en particulier à la fin.
Terminaison
Pour prouver que l’algorithme se termine au bout d’un temps fini, on peut
- ou bien trouver un variant : la taille de la liste restant à trier est un candidat idéal puisqu’à chaque passage dans la boucle, on enlève une carte ce qui fait décroître irrémédiablement ce variant ;
- ou alors utiliser la complexité quadratique dans le pire cas puisque si n<∞ alors n²<∞
Mais la première méthode est préférée, parce qu’elle est au programme.
Remarque
Dès qu’on a montré (comme le demande le programme) qu’il faut moins de n² opérations élémentaires (comparaison, extraction et ajout d’une carte) pour finir le tri, il n’est plus nécessaire de prouver la terminaison puisque n²<∞ dès que n<∞ : l’algorithme se termine en un temps fini puisqu’on a estimé ce temps. Cependant
- Il est des cas où la preuve à l’aide d’un variant est plus facile que l’étude de la complexité.
- En Terminale il sera apprécié que les élèves aient déjà manipulé la notion de variant. Il est bon de répéter le cours pour faciliter son apprentissage.


Algorithme des k plus proches voisins
Activité
Il était initialement prévu de faire l’activité ci-dessous sur des tirages papier (en couleurs) mais le confinement de 2020 en France a forcé à chercher une version utilisable en ligne. C’est le site DocTools qui a été choisi.
Fabrication
Un script Python a été sollicité pour fabriquer des nuages de points, l’un bleu, l’autre rouge, chaque nuage étant formé de points gaussiens dont les paramètres ont été choisis de manière que les nuages s’interpénètrent légèrement. Voici le script :
rom matplotlib.pyplot import *
from random import *
N = 5
X1 = [gauss(3,0.5) for _ in range(N)]
Y1 = [gauss(1,0.5) for _ in range(N)]
X2 = [gauss(5,1) for _ in range(N)]
Y2 = [gauss(2,1) for _ in range(N)]
Xb = [gauss(5,1)]
Yb = [gauss(2,1)]
Xr = [gauss(3,0.5)]
Yr = [gauss(1,0.5)]
plot(X1,Y1,'ro')
plot(X2,Y2,'bo')
plot(Xr,Yr,'yD')
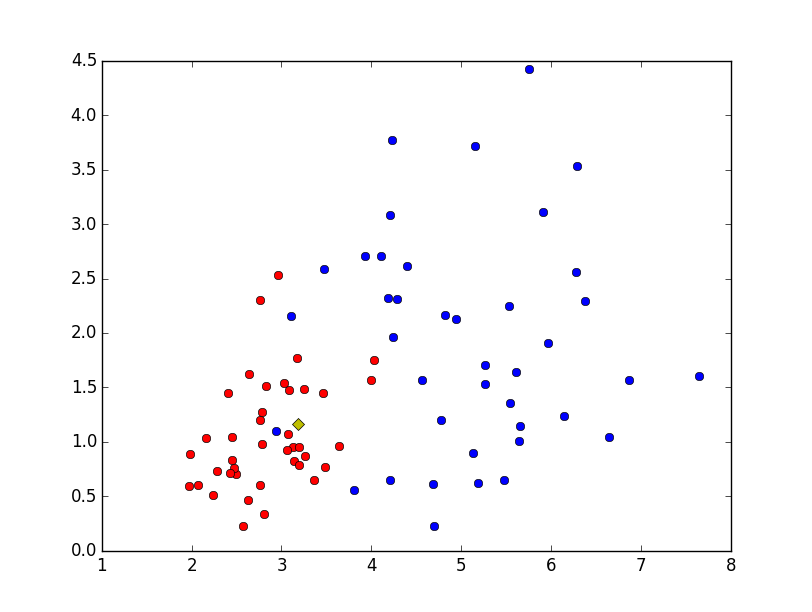
show()Le troisième nuage de points est constitué d’un seul point supplémentaire, ci-dessus choisi rouge. Voici les images obtenues, pour ceux qui souhaiteraient les incorporer dans un QCM ailleurs que sur DocEval :
Puis les images ont été placées dans des QCM à deux réponses « bleu » et « rouge ». Ce QCM a donc été proposé dans le cadre de cette évaluation sur DocEval.
Sondage
Le QCM comportait un « piège » avec cette image où le script Python avait facétieusement placé une fleur bleue en plein milieu des fleurs rouges :
Comme prévu, la majorité des participants tombe dans le piège :
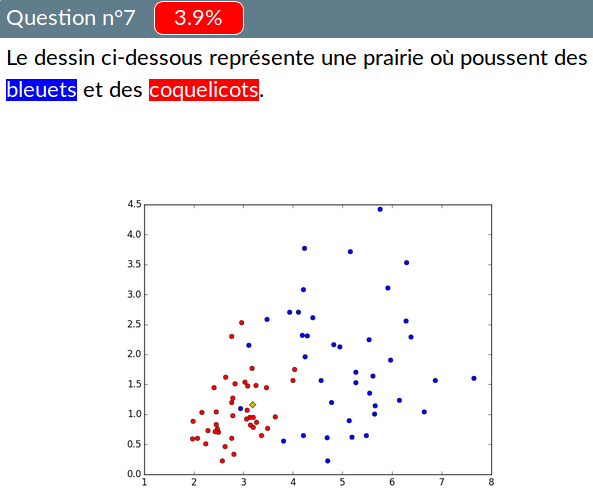
Mais ce n’est pas le cas pour les autres énoncés, moins ambigus :

Ce QCM est en réalité un sondage. Lorsqu’on pense qu’une fleur est bleue, c’est a priori par l’intuition, mais si on essaye de justifier son choix on va assez vite arriver à dire des choses comme « parce qu’il y a une majorité de fleurs bleues au voisinage ». Ainsi
- On arrive naturellement à un consensus sur la couleur de la fleur non encore épanouie.
- Ce consensus n’est pas systématiquement en accord avec la sortie du script Python.
Vers le cours
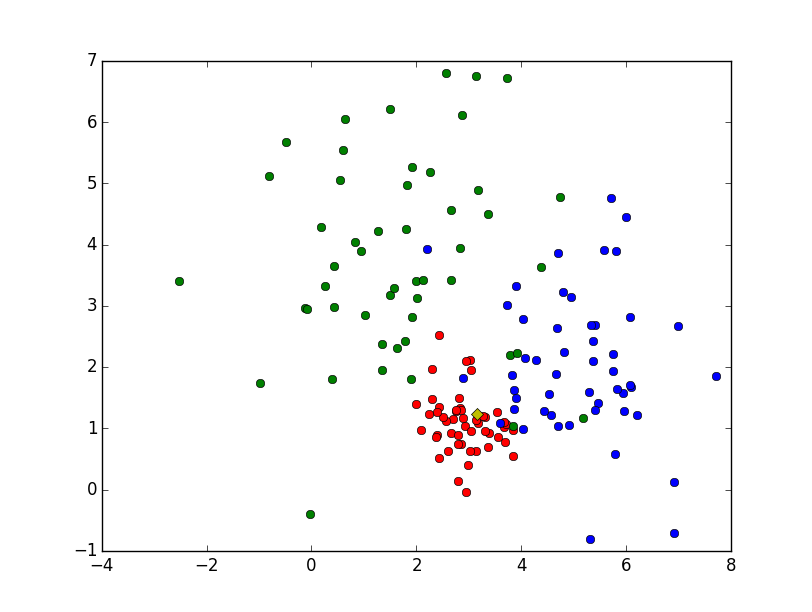
Voici une manière possible d’expliquer pourquoi la fleur ci-dessous est rouge :

Le regard, aidé par le tracé d’un cercle centré sur le point dont la couleur est à déterminer, dit que
- le plus proche voisin est rouge,
- les 2 plus proches voisins sont rouges,
- les 3 plus proches voisins sont rouges,
- les 4 plus proches voisins sont rouges,
- 4 des 5 plus proches voisins sont rouges...
ce qui suggère une forte probabilité que le point de couleur inconnue est, en réalité, rouge (ce qui dans le cas présent est vrai). Et en même temps on gagne un algorithme pour déterminer la couleur probable : prendre la couleur majoritaire parmi les 3 plus proches voisins. Cet algorithme est appelé 3nn (abréviation de « 3 nearest neighbours ») ou « des 3 plus proches voisins ». En fait c’est un cas particulier de la méthode des k plus proches voisins.
k=5
Le choix de k=3 est pertinent lorsqu’il y a deux couleurs possibles, parce que parmi 3 fleurs, il y a forcément une couleur majoritaire (3 est impair). S’il y a 3 couleurs possibles, on court le risque que parmi les trois plus proches voisins, il y ait exactement un rouge, un vert et un bleu. Dans ce cas, on aurait plutôt intérêt à choisir k=5, ce qui évite à la fois les risques d’ex aequo entre 2 couleurs et entre les 3 couleurs.
Apprentissage
La notion d’apprentissage est perceptible avec le « QCM » ci-dessus, mais uniquement par le fait que plus on avance dans l’évaluation, et plus on répond vite.
Pour en faire un vrai apprentissage, il faudrait donner à chaque question la même image mais en dévoilant au fur et à mesure les fleurs. Alors on constaterait que, si on a une chance sur 2 de deviner la bonne couleur à la première question, on devient de plus en plus performant à chaque fois qu’une réponse est donnée (sous forme de corrigé du QCM) et qu’on utilise l’information que fournit ce corrigé.
Le QCM ci-dessus pourrait alors être donné après la phase d’apprentissage.
Voronoï
La théorie de l’algorithme des k plus proches voisins est basée sur une notion géométrique : le diagramme de Voronoi généralisé. Le diagramme de Voronoï classique s’applique à l’algorithme 1nn. Par exemple, à partir du diagramme de Voronoï de ces fruits (chaque cellule est formée des points du plan plus proches du fruit contenu dans la cellule) :

en repassant en traits gras les segments qui séparent une tomate d’une aubergine, on obtient cette zone de séparation :
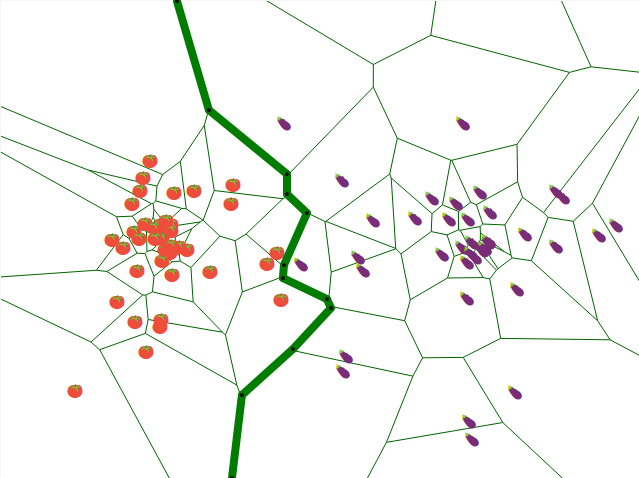
L’algorithme 1nn donne alors cette règle de décision :
- Si le point est à gauche de la frontière verte, il est rouge.
- S’il est à droite de la frontière verte, il est bleu.
Mais pour k plus grand que 1, le dessin du diagramme de Voronoï est plus complexe.
Si les diagrammes de Voronoï font leur retour ici, c’est essentiellement parce qu’une activité débranchée leur avait déjà été consacrée en Seconde.
Remarque historique : Le plus vieux diagramme de Voronoï connu est du à Descartes :

Python
Un fichier css a été préparé pour la reproductibilité de l’activité. Il comprend trois champs :
- l’abscisse du point (un entier engendré aléatoirement),
- l’ordonnée du point (un entier aléatoire aussi),
- et la couleur du point (la chaîne de caractères « bleu » ou « rouge »).
Voici ce fichier :
Le module csv de Python permet d’ouvrir ce fichier, de le lire ligne après ligne. Dans cette lecture on fabrique une liste de couples dont
- le premier élément est la distance entre le point (320,240) et le point coloré,
- et le deuxième élément est la couleur du point connu.
Ensuite on trie ces couples dans l’ordre croissant des distances [2], en définissant une relation d’ordre neighbours entre les couples : le plus petit couple est celui dont la distance à (320,240) est la plus petite.
from csv import *
from math import hypot
def distance(L1,L2):
return hypot(L1[0]-L2[0],L1[1]-L2[1])
point_mystère = (320,240)
table = []
with open('prairie.csv','r') as fichier:
lignes = reader(fichier,delimiter=' ')
for ligne in lignes:
(x,y) = (int(ligne[0]),int(ligne[1]))
couleur = ligne[2]
table.append((distance(point_mystère,(x,y)),couleur))
def neighbours(couple):
return couple[0]
table.sort(key=neighbours)
print([table[k][1] for k in range(3)])On termine en affichant les 3 premiers couples triés, ou plus précisément leur couleur, ce qui permet de décider la couleur du point inconnu simplement en comptant les couleurs et en regardant la couleur majoritaire :
['bleu', 'rouge', 'bleu']
Cours
Remarque arithmétique :
- Sur un point tombé par hasard très près d’un point rouge perdu au milieu de plein de points bleus, l’algorithme 1nn va se tromper.
- L’algorithme 2nn ne garantit pas qu’il existe une couleur majoritaire parmi les 2 examinées : il peut très bien y avoir deux couleurs différentes parmi les deux.
- Par conséquent, le cours ci-dessous porte sur l’algorithme 3nn. Mais s’il y avait 3 couleurs à départager, on risquerait là aussi des ex aequo.
- L’algorithme 4nn présente le même danger que 2nn : il faut que k soit impair pour être certain qu’il y ait une majorité.
- Pour améliorer l’algorithme 3nn, notamment s’il y a 3 couleurs, on passe donc à l’algorithme 5nn.
Plus généralement, s’il y a p couleurs, on doit choisir k divisible par aucun nombre inférieur ou égal à p. Voici les plus petits possibles :
| p | k |
| 2 | 3 |
| 3 | 5 |
| 4 | 5 |
| 5 | 7 |
| 6 | 7 |
| 7 | 11 |
Les nombres premiers font leur apparition en IA !
Voici le cours au format html :

Algorithmes gloutons
Monnaie
Le jeu de cet article permet aussi une activité débranchée (mais avec des vraies pièces de monnaie). Dans ce cadre, l’algorithme glouton consiste à donner les pièces de plus grande valeur possible (tant que ça ne dépasse pas la somme totale) puis continuer avec les pièces de seconde plus grande valeur etc.
Algorithme
Par exemple si on n’a que des pièces rouges,
- on donne autant de pièces de 5 centimes que possible ;
- on complète avec autant de pièces de 2 centimes que possible ;
- on finit si besoin avec une pièce de 1 centime.
En Python cela donne :
def rendu(centimes):
assert centimes==int(centimes) and centimes>0
monnaie = {'\u2464': 0, '\u2461': 0, '\u2460': 0}
while centimes>0:
while centimes>=5:
centimes -= 5
monnaie['\u2464'] +=1
while centimes>=2:
centimes -= 2
monnaie['\u2461'] +=1
while centimes>=1:
centimes -= 1
monnaie['\u2460'] +=1
return monnaieExemple
Le script
for n in range(1,30):
print(rendu(n))produit cet affichage :
1 {'①': 1, '⑤': 0, '②': 0}
2 {'①': 0, '⑤': 0, '②': 1}
3 {'①': 1, '⑤': 0, '②': 1}
4 {'①': 0, '⑤': 0, '②': 2}
5 {'①': 0, '⑤': 1, '②': 0}
6 {'①': 1, '⑤': 1, '②': 0}
7 {'①': 0, '⑤': 1, '②': 1}
8 {'①': 1, '⑤': 1, '②': 1}
9 {'①': 0, '⑤': 1, '②': 2}
10 {'①': 0, '⑤': 2, '②': 0}
11 {'①': 1, '⑤': 2, '②': 0}
12 {'①': 0, '⑤': 2, '②': 1}
13 {'①': 1, '⑤': 2, '②': 1}
14 {'①': 0, '⑤': 2, '②': 2}
15 {'①': 0, '⑤': 3, '②': 0}
16 {'①': 1, '⑤': 3, '②': 0}
17 {'①': 0, '⑤': 3, '②': 1}
18 {'①': 1, '⑤': 3, '②': 1}
19 {'①': 0, '⑤': 3, '②': 2}
20 {'①': 0, '⑤': 4, '②': 0}
21 {'①': 1, '⑤': 4, '②': 0}
22 {'①': 0, '⑤': 4, '②': 1}
23 {'①': 1, '⑤': 4, '②': 1}
24 {'①': 0, '⑤': 4, '②': 2}
25 {'①': 0, '⑤': 5, '②': 0}
26 {'①': 1, '⑤': 5, '②': 0}
27 {'①': 0, '⑤': 5, '②': 1}
28 {'①': 1, '⑤': 5, '②': 1}
29 {'①': 0, '⑤': 5, '②': 2}Attributs
Avec un objet Monnaie on peut simplifier le code en déléguant au porte-monnaie l’affichage de son contenu :
class Monnaie():
def __init__(self,un=0,deux=0,cinq=0):
self.un = un
self.deux = deux
self.cinq = cinq
def __repr__(self):
return '('+str(self.un)+'\u2460 , '+str(self.deux)+'\u2461 ,'+str(self.cinq)+'\u2464 )'Les nombres de pièces de chaque sorte sont maintenant des attributs du porte-monnaie, et on les manipule directement dans le corps de la fonction, qui devient
def rendu(centimes):
bourse = Monnaie()
while centimes>=5:
bourse.cinq += 1
centimes -= 5
while centimes>=2:
bourse.deux += 1
centimes -= 2
while centimes>=1:
bourse.un += 1
centimes -= 1
return bourseEn effectuant
for n in range(20):
print(n,rendu(n))on obtient alors
0 (0① , 0② ,0⑤ )
1 (1① , 0② ,0⑤ )
2 (0① , 1② ,0⑤ )
3 (1① , 1② ,0⑤ )
4 (0① , 2② ,0⑤ )
5 (0① , 0② ,1⑤ )
6 (1① , 0② ,1⑤ )
7 (0① , 1② ,1⑤ )
8 (1① , 1② ,1⑤ )
9 (0① , 2② ,1⑤ )
10 (0① , 0② ,2⑤ )
11 (1① , 0② ,2⑤ )
12 (0① , 1② ,2⑤ )
13 (1① , 1② ,2⑤ )
14 (0① , 2② ,2⑤ )
15 (0① , 0② ,3⑤ )
16 (1① , 0② ,3⑤ )
17 (0① , 1② ,3⑤ )
18 (1① , 1② ,3⑤ )
19 (0① , 2② ,3⑤ )Méthodes
On améliore le résultat en rajoutant des méthodes au porte-monnaie (et en les utilisant pour l’affichage) :
class Monnaie():
def __init__(self,un=0,deux=0,cinq=0):
self.un = un
self.deux = deux
self.cinq = cinq
def pièces(self):
return self.un+self.deux+self.cinq
def total(self):
return self.un+2*self.deux+5*self.cinq
def __repr__(self):
aff = '('+str(self.un)+'\u2460 , '+str(self.deux)+'\u2461 ,'+str(self.cinq)+'\u2464 )'
aff += ' total '+str(self.total())+' cents en '+str(self.pièces())+' pièces'
return affAlors
for n in range(6,20):
print(rendu(n))produit un affichage bien plus riche (!) qu’avant :
(1① , 0② ,1⑤ ) total 6 cents en 2 pièces
(0① , 1② ,1⑤ ) total 7 cents en 2 pièces
(1① , 1② ,1⑤ ) total 8 cents en 3 pièces
(0① , 2② ,1⑤ ) total 9 cents en 3 pièces
(0① , 0② ,2⑤ ) total 10 cents en 2 pièces
(1① , 0② ,2⑤ ) total 11 cents en 3 pièces
(0① , 1② ,2⑤ ) total 12 cents en 3 pièces
(1① , 1② ,2⑤ ) total 13 cents en 4 pièces
(0① , 2② ,2⑤ ) total 14 cents en 4 pièces
(0① , 0② ,3⑤ ) total 15 cents en 3 pièces
(1① , 0② ,3⑤ ) total 16 cents en 4 pièces
(0① , 1② ,3⑤ ) total 17 cents en 4 pièces
(1① , 1② ,3⑤ ) total 18 cents en 5 pièces
(0① , 2② ,3⑤ ) total 19 cents en 5 piècesCela permet d’évaluer l’algorithme glouton, en terme de correction : est-il vrai que le nombre de pièces est minimal (parmi les combinaisons de pièces pour un total donné) ?
La réponse est oui : Jeffrey Shallit appelle canonique un système monétaire pour lequel l’algorithme glouton donne un nombre de pièces minimal pour un total donné. Et il démontre que (①, ② , ⑤) est canonique.
Les systèmes monétaires (ainsi que la programmation objet évoquée dans cet onglet et le précédent) ne sont pas au programme de 1re.
Par contre en Terminale cet exemple est une approche intéressante du programme.
Variant
La somme restant à rembourser est un variant : à chaque étape cette somme diminue de 5 centimes, 2 centimes ou 1 centime, selon la pièce qu’on vient de rembourser.
Par conséquent, il faudra toujours un temps fini pour rendre la monnaie. Heureusement d’ailleurs, le commerce en pâtirait et celui qui est juste derrière dans la file d’attente à la caisse, risquerait de perdre patience.
Le puzzle d’addition binaire n’est pas nécessaire pour faire découvrir le binaire par la manipulation. L’abaque de Neper convient aussi, et nécessite moins de matériel.
Voir également les activités proposées par Marie Duflot-Kremer, dont les suivantes sont intéressantes en 1re :











Commentaires