1. ÉTUDE MATHÉMATIQUE

• Introduction ..... le nombre d’or ..... le nombre d’argent ..... le nombre de cuivre ..... le nombre de nickel ..... le nombre de cobalt ..... le nombre de fer
• Résumé sur les nombres métalliques
• Les angles métalliques

a) Les nombres métalliques : introduction

ÉTUDE DU NOMBRE D’OR

ÉTUDE DU NOMBRE D’ARGENT

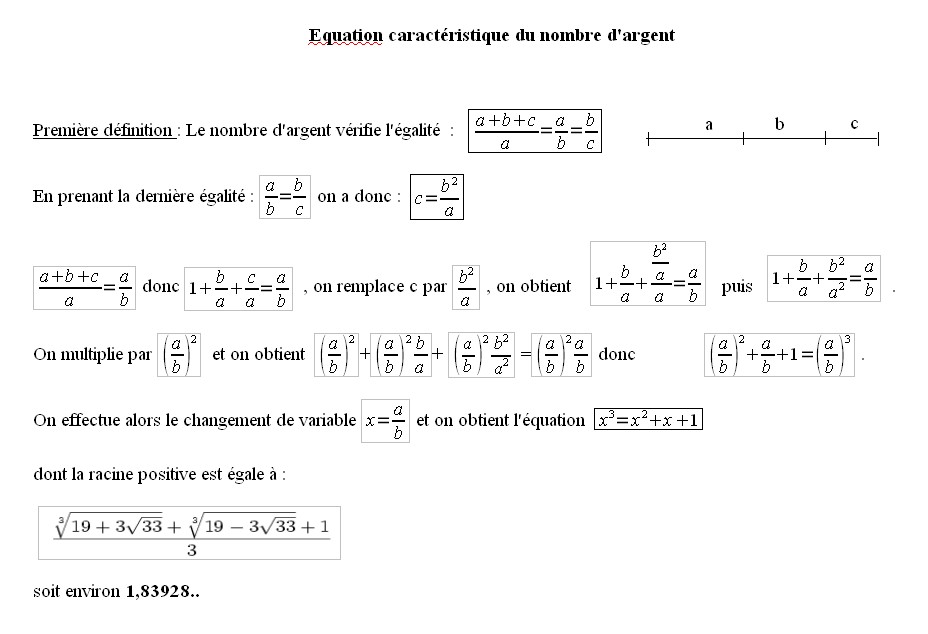
Nous allons partir sur les traces d’Euclide. Comme lui, nous allons étudier le découpage d’un segment.

Euclide avait coupé un segment en deux parties pour aboutir au nombre d’or. Nous le découperons en trois parties pour aboutir à la mise en équation du nombre d’argent.

Cette étude va nous faire découvrir deux nombres d’argent, le premier sera appellé le nombre d’argent et le deuxième sera appelé « proportion d’argent » .

ÉTUDE DU NOMBRE DE CUIVRE

ÉTUDE DU NOMBRE DE NICKEL

ÉTUDE DU NOMBRE DE COBALT

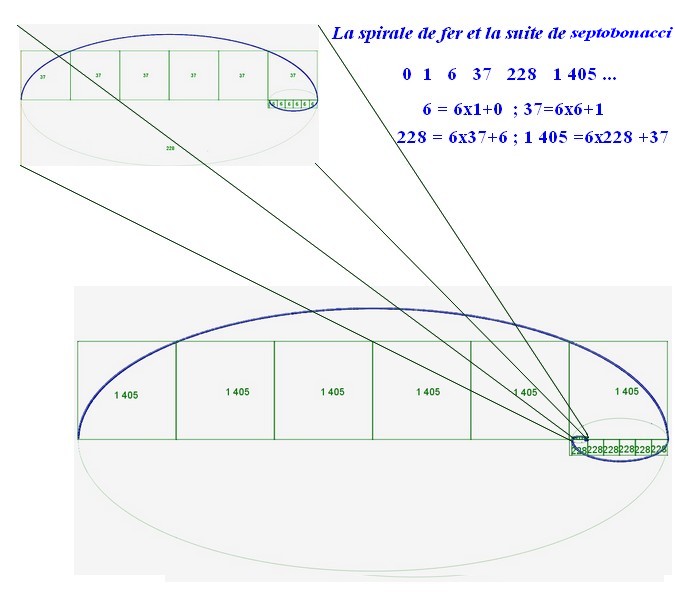
ÉTUDE DU NOMBRE DE FER

Le nombre de fer correspond à un segment coupé en sept parties, qui vérifient la relation ci dessous :

RÉSUMÉ SUR LES NOMBRES MÉTALLIQUES

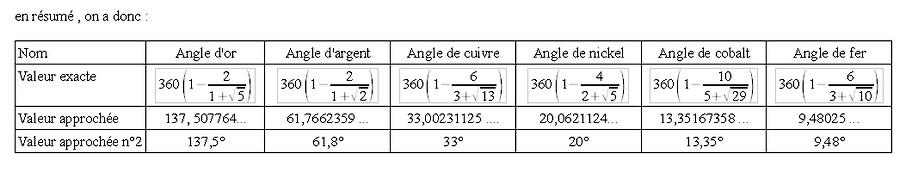
b) Les angles métalliques

2. LES FIGURES GÉOMETRIQUES DE BASE

• Les segments métalliques ..... les rectangles métalliques ..... les triangles métalliques
• Les angles métalliques

TOUTES LES CONSTRUCTIONS GÉOMÉTRIQUES ONT ETE FAITES AVEC LE LOGICIEL CARMETAL.

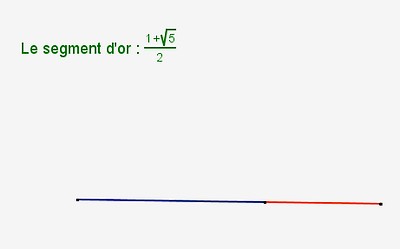
a) Les segments métalliques

segment métallique	construction
or
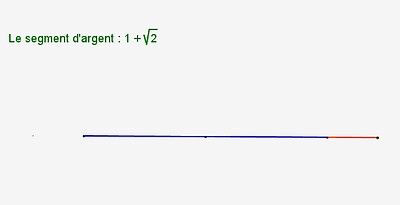
argent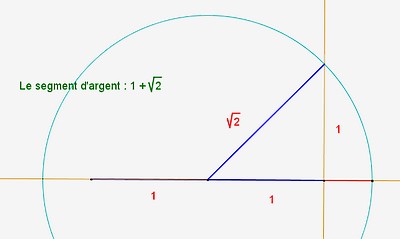
cuivre
nickel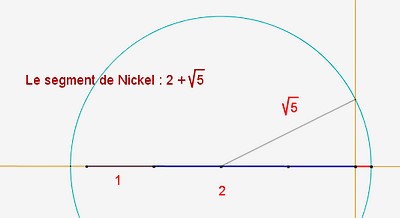
cobalt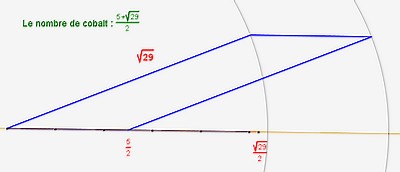
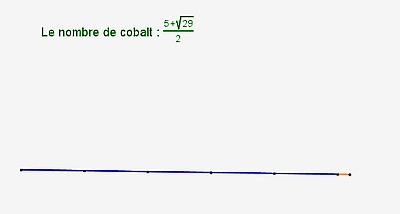
fer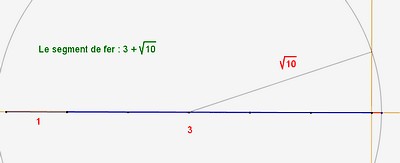

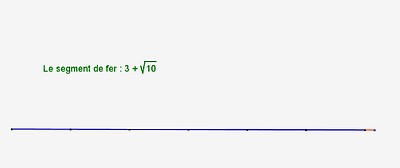
On remarquera que ces segments vérifient les relations de rapports de longueur des proportions métalliques.

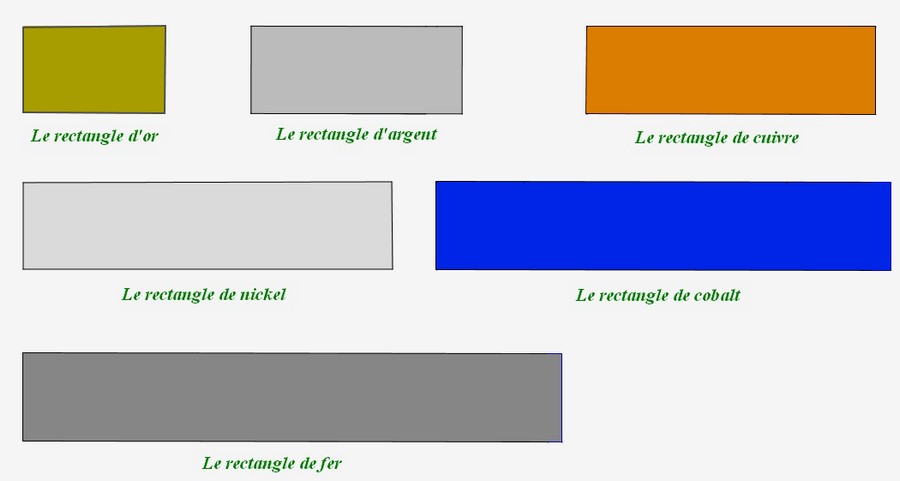
b) Les rectangles métalliques

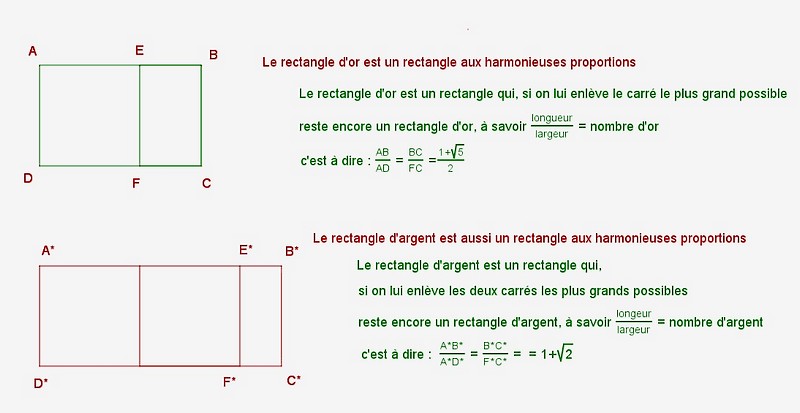
Pour bien comprendre les rectangles métalliques, commençons par comprendre le rectangle d’or et le rectangle d’argent. Ainsi :

Le rectangle de cuivre est le rectangle à qui, si on lui retire les trois carrés les plus grands possibles, reste encore un rectangle de cuivre.

Les rectangles métalliques ont une propriété commune à celle des fractals. C’est la propriété d’auto-similarité. Ainsi, tout rectangle métallique contient un autre rectangle métallique aux mêmes proportions. Ces deux rectangles vérifient la même relation de proportionnalité, à savoir $\frac{longueur}{largeur} $ .

Commençons par les rectangles d’or et d’argent :

rectangle métallique	construction
or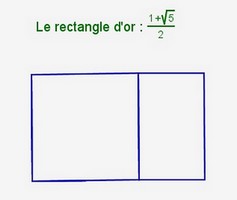
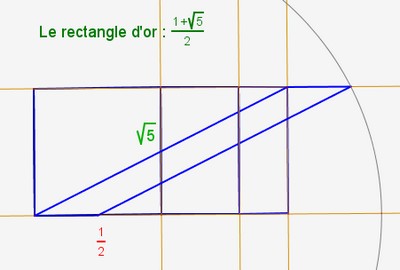
argent

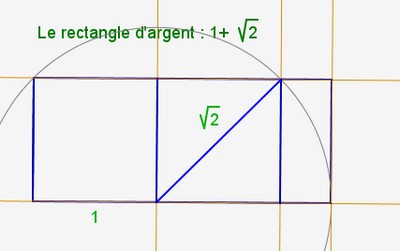
Pour bien comprendre la construction de ces rectangles ainsi que les explications mathématiques, voici des animations CaRMetal que j’ai filmées sur le rectangle d’or et le rectangle d’argent :

Constructions et explications du rectangle d’or :

Ici, on prend un carré de côté égal à 2 mais on aurait très bien pu prendre un carré de côté égal à 1 comme dans les constructions précédentes.

— - voir l’animation« construction du rectangle d’or » jointe à la fin de l’article ----------

Constructions et explications du rectangle d’argent :

— - voir l’animation « construction du rectangle d’argent » jointe à la fin de l’article ----------

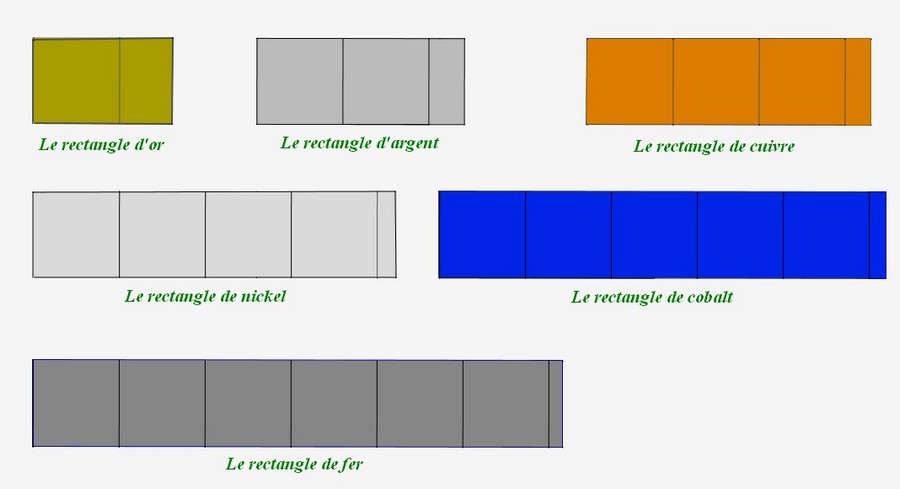
Voici maintenant les autres rectangles métalliques :

rectangle métallique	construction
cuivre
nickel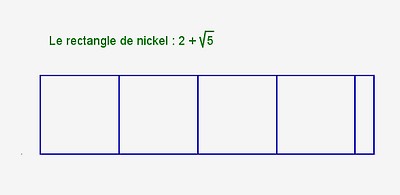
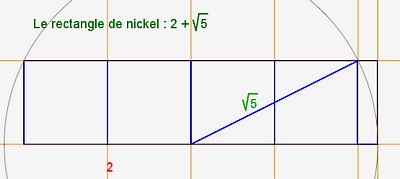
cobalt
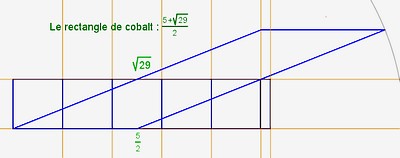
fer

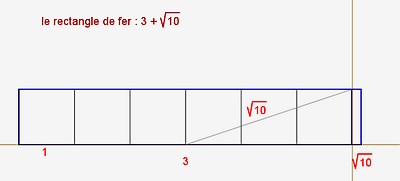
Comparons les rectangles métalliques :

– premièrement avec leurs carrés et leur rectangle similaire :

– deuxièmement les rectangles métalliques sans leurs carrés :

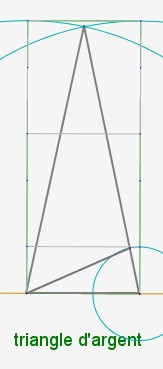
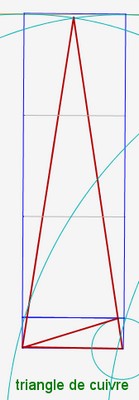
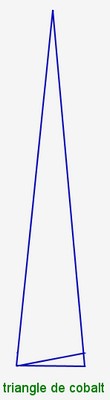
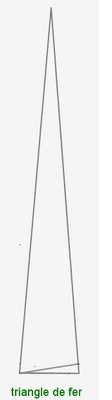
c) Les triangles métalliques

Un triangle métallique est un triangle isocèle qui respecte les proportions $\frac{cote}{base} $ = proportion métallique. Il contient lui même un autre triangle qui a les mêmes proportions. Ainsi, comme les rectangles métalliques , les triangles métalliques ont la propriété d’auto similarité.

Pour construire un triangle métallique, on trace un rectangle métallique et on reporte la longueur du rectangle sur le côté du triangle isocèle.

Pour mieux comprendre :

– construction et explication du triangle d’or :

— - voir l’animation « construction du triangle d’or » jointe à la fin de l’article ------------

– construction du triangle d’argent (c’est le même procédé de construction que pour le triangle d’or) :
— - voir l’animation « construction du triangle d’argent » jointe à la fin de l’article ----------

Voici donc les triangles métalliques :

construction	figure	construction	figure

Comparons les triangles métalliques obtenus :

d) les angles métalliques

Les angles métalliques ont été déjà étudiés dans l’étude mathématique (voir plus haut. On avait en résumé :

3. SPIRALES ET AUTRES FIGURES

• Spirale d’or ..... spirale d’argent ..... spirale de cuivre ..... spirales de nickel ..... spirales de cobalt ..... spirales de fer
• Comparatif des coquillages métalliques
• Les boules d’or et d’argent ..... les ellipses métalliques ..... les losanges métalliques ..... les polygones métalliques

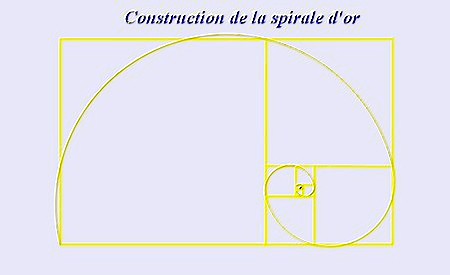
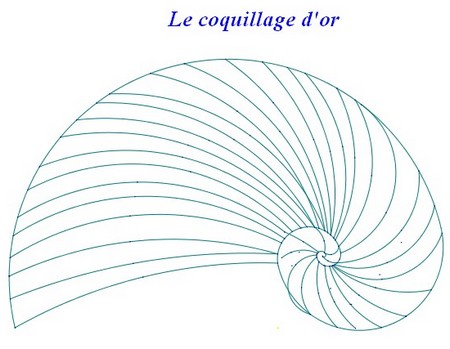
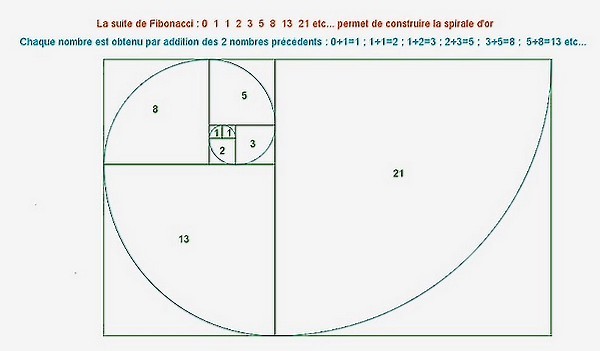
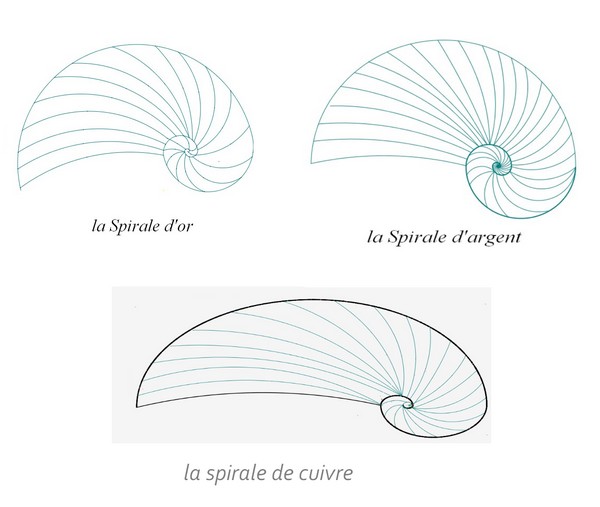
a) La spirale d’or

Le but est de créer des rectangles d’or et de joindre des arcs de cercle. voici l’explication de la construction de cette spirale d’or :

b) La spirale d’argent

Je n’ai trouvé nulle part la spirale d’argent, j’ai donc décidé de la créer. Mais contrairement à la spirale d’or, je ne pouvais imbriquer les rectangles d’argent à l’intérieur du premier rectangle d’argent. J’ai eu l’idée de décaler chaque rectangle d’argent de manière à continuer la spirale d’argent.

Pour bien comprendre la construction de cette spirale d’argent, ouvrir le diaporama ci dessous :

Voici le résultat :

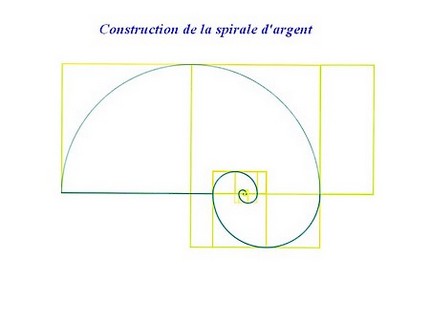
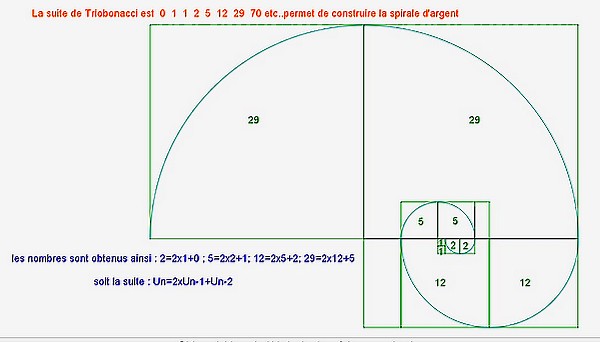
Voici une comparaison des spirales d’or et d’argent :

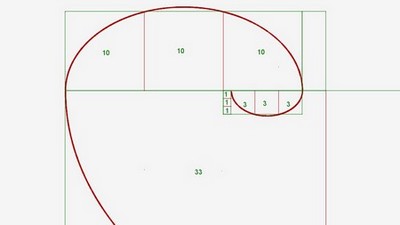
c) La spirale de cuivre

Pour créer la spirale de cuivre, il fallait partir du rectangle de cuivre, qui a trois carrés. Ne pouvant créer un cercle passant par quatre points des carrés, j’ai donc utilisé une ellipse qui passe par ces quatre points et par un cinquième point qui est symétrique à l’un des points de l’ellipse par rapport à l’axe passant par les côtés inférieurs des carrés.

La spirale de cuivre est donc de type elliptique contrairement aux spirales d’argent et d’or qui, elles, sont des spirales concentriques.

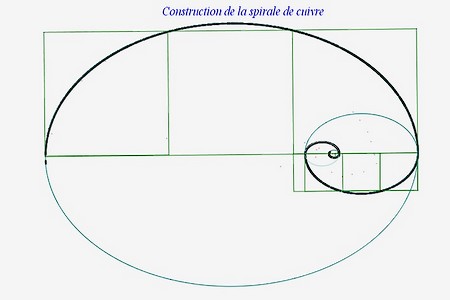
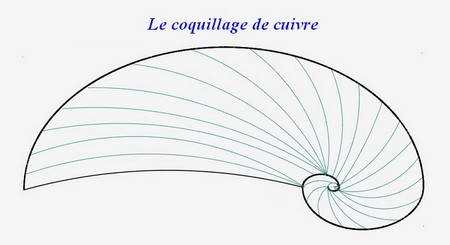
On peut également tracer une spirale de cuivre avec la suite de quartobonacci qui lui est associée. Cette spirale se déroule en trois étapes :

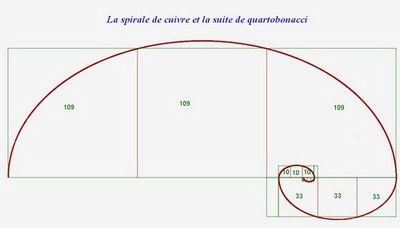
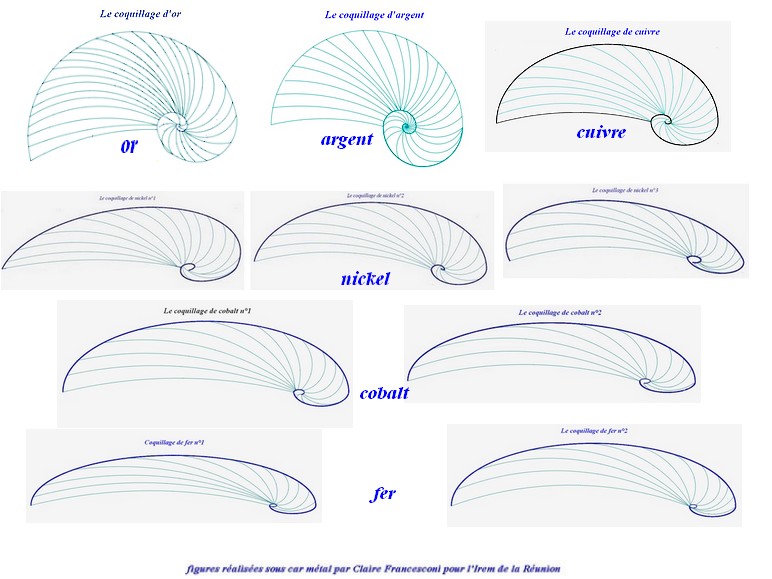
Voici la comparaison des coquillages métalliques précédents :

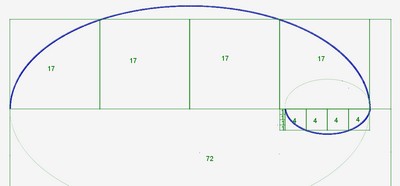
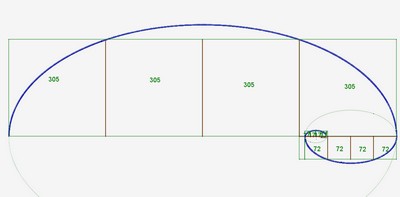
d) Les spirales de nickel

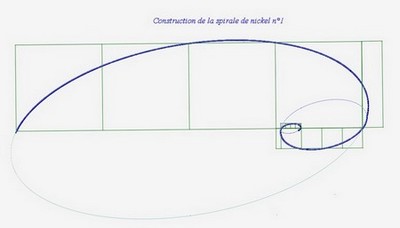
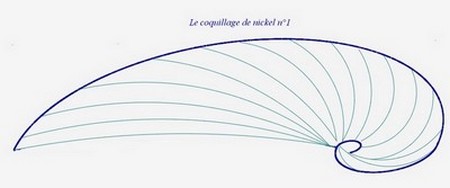
J’ai trouvé trois spirales de nickel. En effet, il y a trois possibilités d’ellipse passant par les plus grand nombre de sommets des carrés.

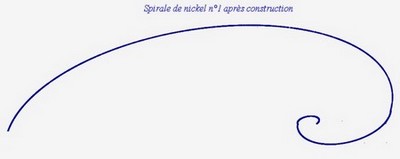
Voici la spirale de nickel n°1 :

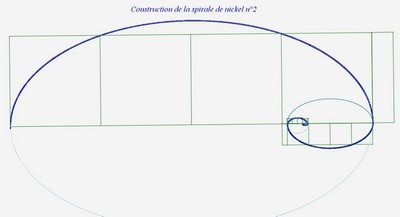
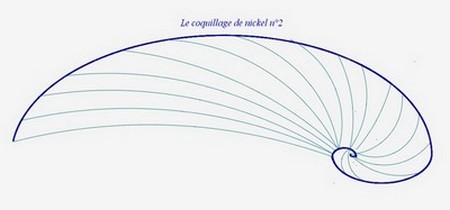
Voici la spirale de nickel n°2 , elle est plus symétrique :

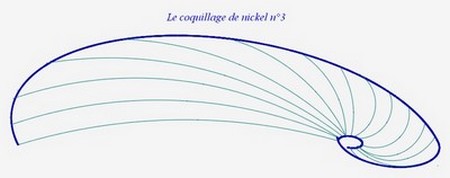
Voici la spirale de nickel n°3 :

On peut également tracer une spirale de nickel avec la suite de quintobonacci qui lui est associée. Cette spirale se déroule en trois étapes :

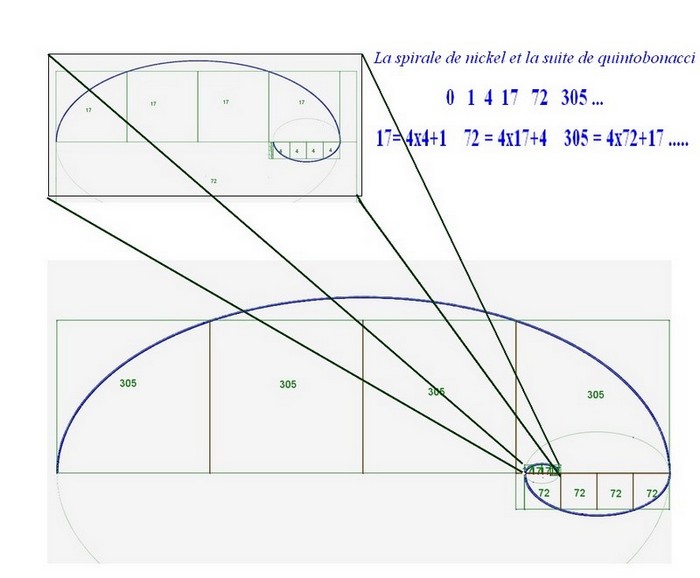
Comparons les trois coquillages de nickel :

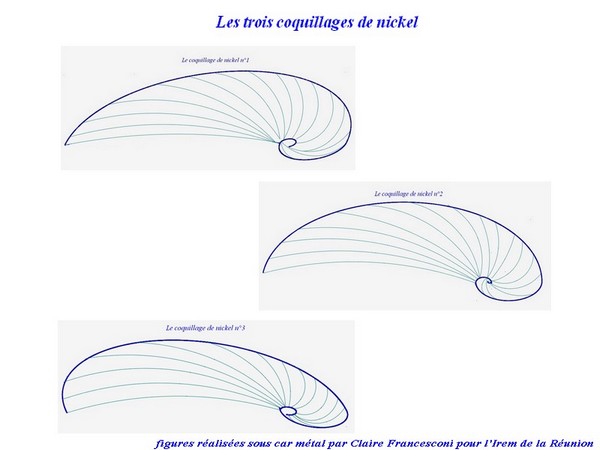
Je prendrai dorénavant les spirales qui sont les plus symétriques.
Ainsi, la spirale de nickel retenue est la spirale de nickel n°2 .

e) Les spirales de cobalt

Il y a 8 ellipses de cobalt possibles.

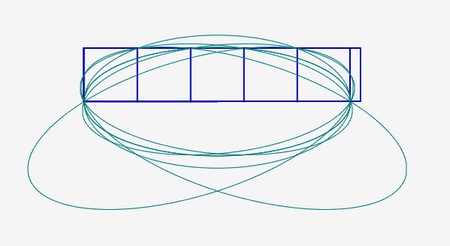
Parmi ces ellipses, deux seulement sont symétriques.

Voici la spirale de cobalt n°1 :

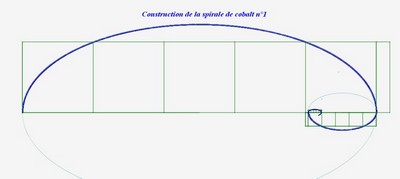
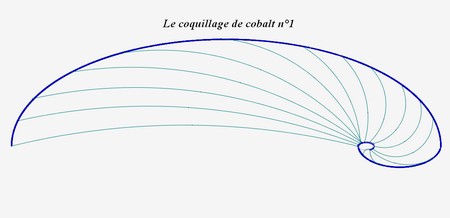
Voici la spirale de cobalt n°2 :

On peut également tracer une spirale de cobalt avec la suite de sixobonacci qui lui est associée. Cette spirale se déroule en trois étapes :

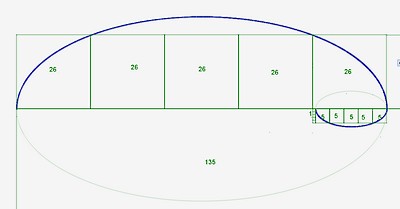
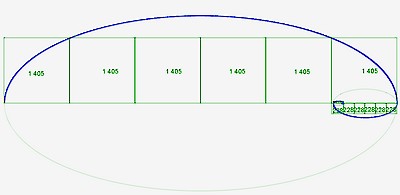
f) les spirales de fer

Il a y au moins 8 ellipses de fer.

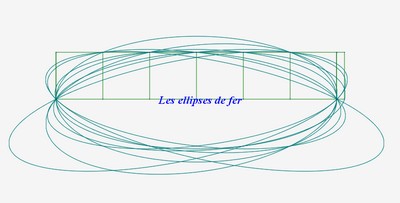
Parmi ces ellipses, deux seulement sont symétriques.

Voici la spirale de fer n°1 :

|

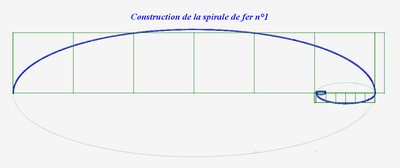
Voici la spirale de fer n°2 :

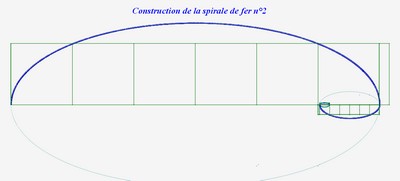
On peut également tracer une spirale de fer avec la suite de septobonacci qui lui est associée. Cette spirale se déroule en trois étapes :

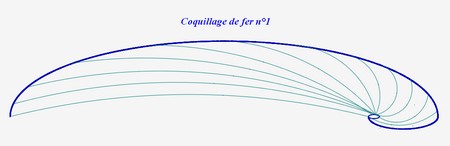
Et pour finir, voici donc un comparatif des coquillages métalliques :

g) Figures géométriques issues du nombre d’or ou du nombre d’argent

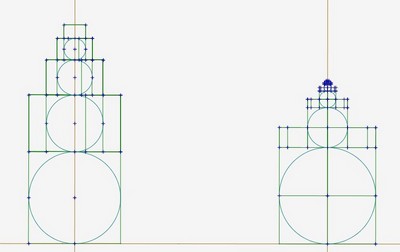
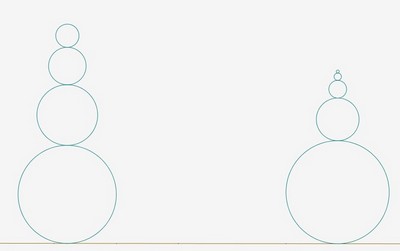
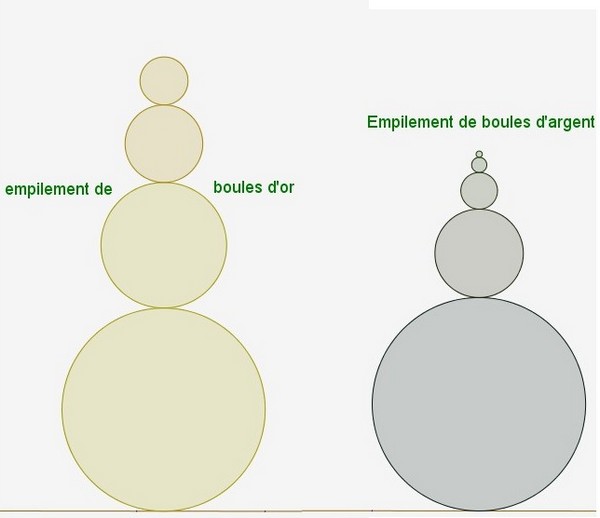
Voici des empilements de boules d’or et de boules d’argent :

On va utiliser le même processus de construction que pour les spirales métalliques, mais sans les emboiter les unes dans les autres .

Le principe est le suivant : on crée deux rectangles métalliques identiques. puis on trace un cercle passant par ces deux rectangles. On déplace les deux petits rectangles métalliques contenus dans les grands au dessus des carrés et on recommence.

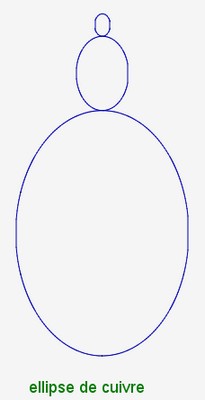
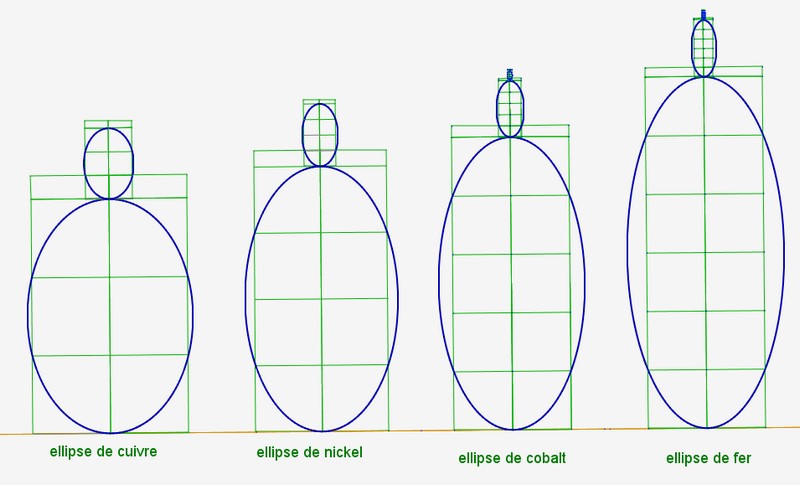
Voici des empilements d’ellipses métalliques :

Là aussi, on va utiliser le même processus de construction que pour les spirales métalliques, mais sans les emboiter les unes dans les autres .

Le principe est le suivant : On crée deux rectangles métalliques identiques. puis on trace une ellipse passant par ces deux rectangles. On déplace les deux petits rectangles métalliques contenus dans les grands au dessus des carrés et on recommence.

construction	figure obtenue

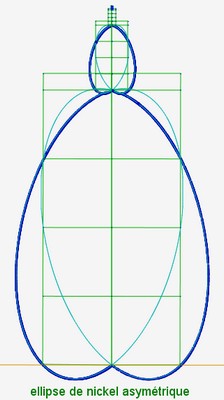
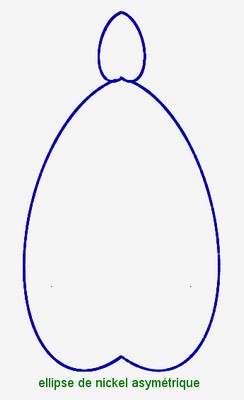
Voici un exemple de construction avec une ellipse de nickel asymétrique (voir coquillage de nickel n°1) :

construction	figure obtenue

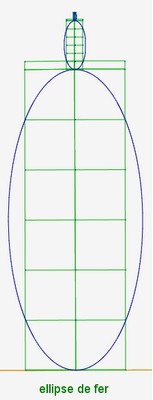
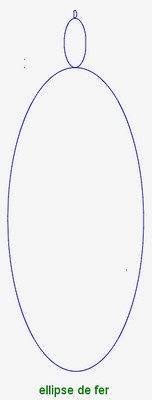
Il y a aussi les figures issues d’ellipses de cobalt et de fer.

construction	figure obtenue

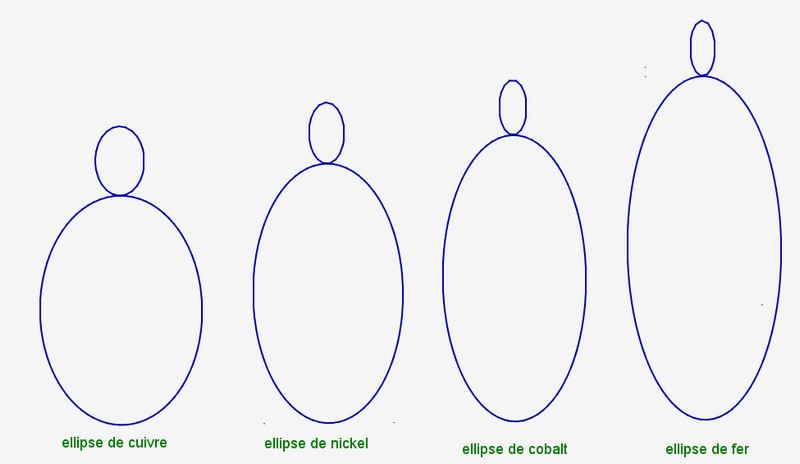
Comparons maintenant les ellipses métalliques :

Les losanges métalliques :

Le principe des losanges métalliques est le suivant : on prend un rectangle métallique, et on veut tracer le petit rectangle métallique qui lui est associé à l’intérieur du grand rectangle afin de tracer les deux losanges qui leurs sont associés.

Pour cela, on va effectuer deux transformations : la première transformation est une translation qui permet de centrer le petit rectangle métallique. La deuxième transformation est une rotation de 90° qui va permettre de le faire pivoter sur lui même de 90°.

Le diaporama ci dessous résume ces différentes étapes de construction de losanges métalliques.

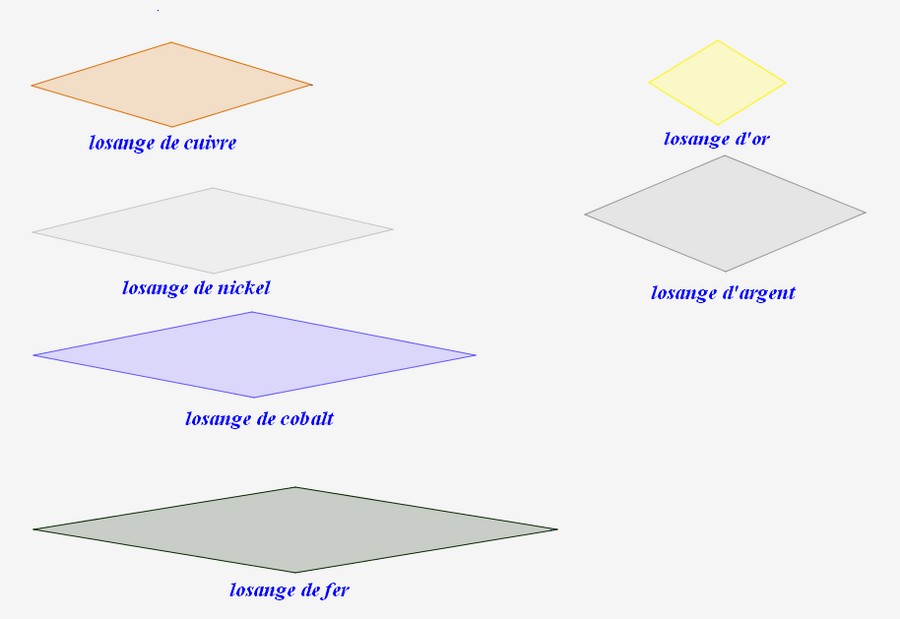
Voici les 6 losanges métalliques :

losange métallique	construction
or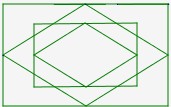
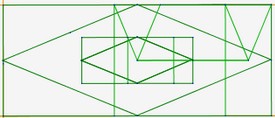
argent
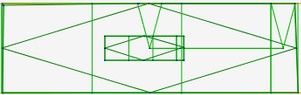
cuivre
nickel
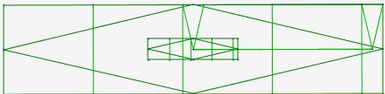
cobalt
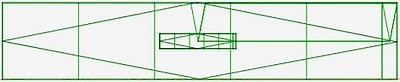
fer

Comparons les losanges métalliques obtenus :

Les polygones métalliques :

Je n’ai trouvé pour l’instant que le pentagone à base de triangles d’or. Je compte bien en trouver ultérieurement.

LES AUTRES PARTIES, HISTOIRE ET ARTS SERONT TRAITÉES DANS UN AUTRE ARTICLE.

4. HISTOIRE DU NOMBRE D’OR

5. LES ARTS ET LES NOMBRES MÉTALLIQUES

a) Peinture

b) Architecture

c) Musique