Le jeu icosien a été inventé au milieu du XIXe siècle par William Rowan Hamilton, astronome irlandais.
Voici la description, par Édouard Lucas, du jeu icosien :

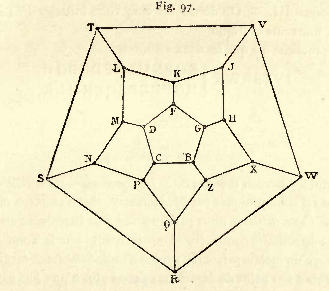

Le jeu icosien comme jeu vidéo
Puisque le jeu icosien est un jeu en 2D, on peut envisager de le programmer avec phaser.io qui est un logiciel de création de jeux en 2D.
Programmation en Phaser
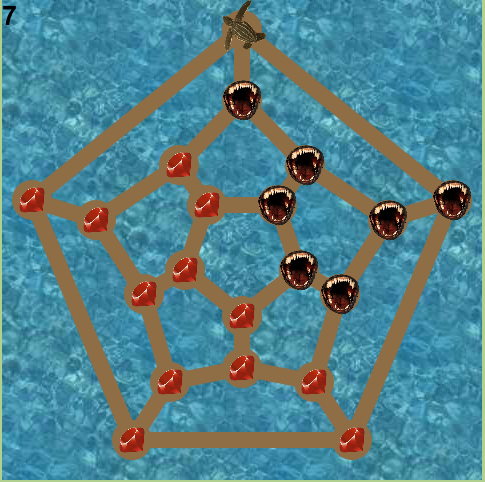
Voici donc la variante imaginée : Le héros est une tortue marine, qui évolue sur des bancs de sable entourés d’un océan hostile (il y a plein de requins, friands de tortues). La tortue quitte son nid (en haut de l’image) et doit ramasser tous les rubis. Mais chaque fois qu’elle ramasse un rubis, cela déclenche la floraison d’une plante carnivore mangeuse de tortues, et la tortue a tout intérêt à quitter ce lieu devenu dangereux (et à n’y pas revenir). Elle est chargée de ramasser tous les rubis et de revenir à son point de départ. Voici le plateau de jeu tel que rendu par Phaser :

L’océan est une image de fond, le sable est un dessin fait par-dessus ce fond (les arêtes sont des segments en traits épais et les sommets sont des disques). Par-dessus tout ça, sont placés des bouches pleines de dents (au départ, cachées) et des rubis, sauf sur le premier sommet, où se trouve une tortue. Celle-ci est formée de plusieurs images ce qui donne l’impression qu’elle est animée (elle marche l’amble). Dans le vocabulaire de Phaser, les rubis, tortue etc sont des « sprites » (remarque : Ce mot a été repris dans Scratch, qui permet aussi de programmer ce jeu, sauf qu’il n’y a pas de facilités pour les graphes). Phaser gère aisément les sprites et les le dessin, mais n’a pas par défaut de bibliothèque de graphes. On va donc en créer une pour se faciliter la programmation du jeu.
Graphes
Phaser possède beaucoup d’objets prédéfinis comme text, sprite, point, line ou circle mais pas de fonctions sur les graphes. Il est donc nécessaire d’en créer. Le choix qui a été fait ici est de faire un objet JavaScript à deux variables :
- graphe.nodes est un tableau de points (des Phaser.Point gracieusement fournis par Phaser) ;
- graphe.edges est un tableau contenant des tableaux d’entiers : Pour le sommet numéro n, graphe.edges[n] est la liste des sommets auxquels il est relié.
Par exemple, le graphe chemin du dodécaèdre a pour arêtes :
chemin.edges = [ [1,2,5], [3,6], [4,7], [4,8], [9],
[10,11], [10,12], [11,13], [12,14], [13,14],
[15],[16],[17],[18],[19],
[16,17],[18],[19],[19],[]
];Pour chemin.nodes il vaut mieux boucler : Répéter 20 fois les actions suivantes :
- lire l’abscisse x du sommet n dans le tableau des abscisses (abcs[n]) ;
- lire l’ordonnée y (ords[n]) dans le tableau des ordonnées ;
- créer un point Phaser de coordonnées (x,y) avec new Phaser.Point(x,y) ;
- ajouter ce point à chemin.nodes qui est initialement vide.
Cet algorithme se traduit ainsi en JavaScript :
function addNode(graphe,x,y){
graphe.nodes.push(new Phaser.Point(x,y));
}Avec ça la construction du graphe du dodécaèdre se fait avec ce code :
var chemin = [ ];
chemin.nodes = [ ];
var abcs = [240,30,450,130,350,240,94,386,168,312,177,303,142,338,240,205,275,183,297,240];
var ords = [30,200,200,440,440,100,220,220,382,382,165,165,294,294,368,205,205,270,270,316];
for (var n in abcs) { addNode(chemin,abcs[n],ords[n]) }auquel il faut rajouter le tableau chemin.edges défini plus haut.
Dessin
Ensuite, vient la question de savoir comment on dessine le graphe. Pour cela,
- pour chaque arête du graphe, on trace un segment joignant les deux sommets qu’elle joint, de couleur sable, et d’épaisseur 16 pixels ;
- pour chaque sommet du graphe, on trace un disque, également de couleur sable, de rayon 24 pixels (il faut que tout le rubis soit dans le sable)
Pour que les traits et remplissages soient couleur de sable, on fait
graphique.z = 2;
graphique.lineStyle(16,0x8F6D45);
graphique.beginFill(0x8F6D45); (la couleur du sable a été obtenue avec l’outil « pipette » de Gimp, sur une photo de vrai sable). La variable graphique est un graphique de Phaser, obtenue avec
var graphique = game.add.graphics(0,0);
On lui a donné le numéro de calque z=2 pour qu’elle ne cache pas la tortue (qui, elle, aura le numéro z=3 pour rester en permanence au-dessus du sable).
Pour dessiner les sommets du graphe, on utilise la primitive circle de Phaser : On lui fournit P.x, P.y et le rayon, P étant un point de Phaser obtenu par lecture du tableau des sommets (qui sont justement des points de Phaser). Le nuage de points se dessine ainsi :
for(var s in g.nodes){
graphique.drawCircle(g.nodes[s].x,g.nodes[s].y,24);
}En examinant le code source complet, on constate qu’en fait il y a quelque chose en plus pour les sommets autres que le premier : Le placement d’un rubis, qui est un sprite de Phaser, aux coordonnées x et y, mais ancré à 0,5 pour le centrer et rapetissé avec scale=0.25.
Pour éviter les mauvaises surprises, on a intérêt à terminer le dessin par graphique.endFill() qui arrête de remplir automatiquement en couleur sable les dessins ultérieurs.
Pour le dessin des segments, c’est un peu plus long :
- il faut boucler sur les sommets dep servant de départ aux segments ;
- Dans cette boucle, il faut boucler sur toutes les destinations jointes à dep, en bouclant sur les numéros d’arrivée possibles na in g.edges[dep], et pour chaque na, calculer le sommet d’arrivée avec arr = g.edges[dep][na] ;
- Là, on place le stylo sur le point dep, puis on trace un segment jusqu’au point arr :
for(var dep in g.edges){
for(var na in g.edges[dep]) {
var arr = g.edges[dep][na];
graphique.moveTo(g.nodes[dep].x,g.nodes[dep].y);
graphique.lineTo(g.nodes[arr].x,g.nodes[arr].y);
}
}Les dessins des segments et disques ainsi que le placement des rubis sont regroupés dans une fonction dessineGraphe admettant comme antécédent un graphe comme celui défini ci-dessus. Il suffira donc d’appliquer cette fonction pour que le graphe soit dessiné.
Parcours d’une arête
Pour que la tortue puisse glisser le long d’une arête suffisamment lentement pour qu’on la voie glisser, on a besoin d’une fonction promenade(P1,P2) qui
- place la tortue sur le point P1 (départ de la promenade) ;
- oriente la tortue vers P2 (avec conversion en degrés de l’angle calculé) ;
- crée une animation de type « tween » à vitesse linéaire et de durée 20 fois la distance à parcourir ;
- ajoute la mission à accomplir à la fin de l’animation : manger un rubis (fonction définie plus bas).
En Phaser, cela se code ainsi :
function promenade(P1,P2){
turtle.x = P1.x;
turtle.y = P1.y;
turtle.angle = Phaser.Point.angle(P2,P1)*180/Math.PI;
P2.angle = turtle.angle;
var voyage = game.add.tween(turtle).to(P2,20*P1.distance(P2),"Linear",true);
voyage.onComplete.add(manger);
}Analyse du graphe
Pour raccourcir le code, on crée une fonction booléenne disant s’il y a une arête entre deux sommets considérés (sinon la tortue nagerait au milieu des requins pour aller du premier sommet au second, la pauvre...).
Mais pour définir cette fonction, il faut d’abord en définir une autre disant si un tableau contient un élément donné, la fonction « in » de JavaScript ne fonctionnant pas bien dans ce contexte :
- on crée un booléen local appelé rep (comme « réponse ») et initialement faux ;
- on boucle dans le tableau ;
- si à un moment l’élément lu dans le tableau est égal à l’élément qu’on y cherche, rep devient vrai puisqu’alors le tableau contient bien l’élément ;
- si à la fin de la boucle, rep est toujours fausse, c’est qu’on n’a pas trouvé l’élément dans le tableau dans une recherche exhaustive, et que le tableau ne contient pas l’élément. Cette variable est donc celle à retourner.
En JavaScript, ça donne ça :
function contient(tableau,element){
var rep = false;
for (var e in tableau){
if (tableau[e] == element) {rep=true}
}
return rep;
}Avec cette fonction, l’existence d’une arête entre deux sommets a et b se résume à une disjonction :
- Ou bien il y a une arête allant de a vers b ;
- ou bien il y a une arête allant au contraire de b vers a.
Ce qui donne cette fonction en JavaScript :
function liaison(a,b){
return (contient(chemin.edges[a],b) || contient(chemin.edges[b],a));
}Choix d’une destination
Une question n’a pas encore été abordée jusqu’ici : Comment fait-on pour jouer à ce jeu ? Autrement dit, comment le joueur va-t-il choisir où mener la tortue ? Le plus direct, c’est encore que le joueur clique (ou tape) sur la destination choisie. Seulement, avec des graphes un peu compliqués, ce choix devient vite un jeu d’adresse...
On a donc choisi que dès lors que le clic ou tap a été effectué, le sommet choisi soit celui le plus proche de là où on a cliqué ou tapé. Le jeu marche plutôt bien comme ça. On a donc besoin d’un algorithme permettant de trouver quel est le sommet du graphe le plus proche de la souris. Pour cela, on détermine la distance minimale entre la souris et tous les sommets du graphe, et dans la boucle, on mémorise le numéro du sommet : Ainsi, à la fin de la boucle, on a bien le numéro du sommet le plus proche :
function prochain(x,y){
var dmin = 1e6;
var numero = -1;
for (var n in chemin.nodes){
if (Phaser.Math.distance(x,y,chemin.nodes[n].x,chemin.nodes[n].y)<dmin){
numero = n;
dmin = Phaser.Math.distance(x,y,chemin.nodes[n].x,chemin.nodes[n].y);
}
}
return numero;
}Animation
L’objet essentiel de Phaser est le sprite (comme dans Scratch en fait), qui est une image sur fond transparent, plaçable et déplaçable dans l’écran de jeu. Dans le jeu icosien, la structure de l’image est, dans l’ordre des z croissants :
- le fond qui est une image pavable (un « tileSprite » de Phaser) représentant l’eau ;
- le graphe défini ci-avant, avec des sprites représentant des rubis (non déplaçables, ils vont juste se faire manger par la tortue et alors disparaître) ;
- les plantes carnivores qui sont des sprites représentant une bouche pleine de dents, et eux non plus ne bougent pas comme le font les personnages d’un jeu : Ils apparaissent lorsque la tortue a visité un sommet, pour montrer que le sommet est interdit de passage.
- Et la tortue qui est un sprite animé (elle marche en permanence). Ceci est un peu plus complexe que le placement d’un sprite simple.
Par exemple, pour placer des rubis dans le jeu, on commence par déclarer une variable de type « sprite » qui contient l’image suivante :

La déclaration de la variable se fait dans une fonction appelée « preload » parce que c’est là que Phaser fait tout ce qu’il y a à faire avant de créer le jeu :
game.load.spritesheet("rubis","img/rubygem.png");
(le nom « rubis » a été donné au sprite ce qui permet de le nommer ensuite dans le script, et le second paramètre est le chemin vers le nom du fichier représentant l’image ci-dessus)
Dorénavant, chaque fois que l’on veut placer un rubis dans le jeu, on ajoute juste un sprite de type « rubis » en fournissant les coordonnées initiales du rubis. Ici, on le fait sur tous les sommets du graphe sauf le premier (d’indice 0 : La tortue est déjà dessus) :
for(var s in g.nodes){
graphique.drawCircle(g.nodes[s].x,g.nodes[s].y,24);
if(s>0){
gemmes[s] = game.add.sprite(g.nodes[s].x,g.nodes[s].y,"rubis");
gemmes[s].anchor.setTo(0.5);
gemmes[s].scale.setTo(0.25);
}
}Une fois le sprite ajouté (« add »), il est nécessaire de le centrer sur le sommet en plaçant son point d’ancrage à 0.5 puis de le rapetisser en lui appliquant une homothétie de rapport 0.25 (ça tombe bien, les homothéties sont au programme du cycle 4).
Pour la tortue, on a vu que c’est plus compliqué. En fait, l’image elle-même est déjà plus complexe, puisqu’elle est formée de plusieurs images de la tortue, représentant les phases successives du mouvement :
En bref, une sorte de frise a été faite en juxtaposant 8 images de 100 pixels de large et 121 pixels de haut, pour une image finale de 800 pixels de large par 121 pixels de haut, qui est celle que l’on voit ci-dessus. On s’en doute, il faudra expliquer à Phaser que l’image doit être découpée en 8 morceaux, et donner les dimensions de chacun des morceaux. Cela se fait dans la fonction preload de Phaser :
game.load.spritesheet("tortue","img/tortue.png",100,121,8);
C’est la présence de ces paramètres numériques qui fait que la tortue n’est pas un sprite comme les autres puisqu’il a plusieurs couches (8 au total) ce qui permet de l’animer. Pour placer et animer la tortue, on effectue les opérations suivantes :
- ajouter (« add ») dans le jeu, un sprite de type « tortue », aux coordonnées (240,30) ;
- le placer (avec z=3) dans le calque tout en haut, pour être certain de le voir en permanence ;
- le centrer sur le point de coordonnées (240,30) en mettant son point d’ancrage à 0,5 ;
- le rapetisser d’un facteur 2 afin qu’il n’envahisse pas tout l’écran ;
- le diriger vers le bas (où se trouve un sommet accessible) en mettant son angle à 90 ;
- créer une variable d’animation walk en la plaçant (« add ») dans les animations de la tortue ;
- lancer l’animation walk en la paramétrant à 16 images par seconde (soit 2 cycles par seconde) et en rendant cette animation cyclique (« true ») ;
En JavaScript cela s’écrit
turtle = game.add.sprite(240,30,"tortue");
turtle.z = 3;
turtle.anchor.setTo(0.5);
turtle.scale.setTo(0.5);
turtle.angle = 90;
var walk=turtle.animations.add("walk");
turtle.animations.play("walk",16,true);Moteur du jeu
On a vu que les rubis sont des sprites de Phaser et en fait, quand on place un rubis sur chaque sommet du graphe, on met à jour un tableau appelé gemmes, qui, au cours du jeu, contient donc les rubis visibles du jeu. Lorsque la tortue arrive sur un sommet de numéro n, on doit donc enlever le rubis gemmes[n] et le remplacer par une plante carnivore. Cela se fait dans la fonction manger() qui, on l’a vu, est appelée à chaque fin de promenade (quand la tortue arrive au second sommet de l’arête qu’elle parcourt à vitesse de tortue). On va donc commencer par décrire cette fonction. Pour cela, on a besoin de 4 nouveautés dans le jeu :
- une variable richesse, initialement nulle, représentant le nombre de rubis récoltés par la tortue ;
- une variable lieu indiquant le numéro du sommet où se trouve actuellement la tortue ;
- un tableau possible donnant, pour chaque numéro de sommet, le caractère visitable ou non de ce sommet ;
- un texte aff en haut à droite du jeu, qui permet de savoir à tout moment du jeu, où on en est (ceci est facultatif, il suffit de compter les plantes carnivores pour connaître la variable richesse).
La création du texte dans le jeu se fait dans la fonction create de Phaser (là où on a créé l’animation de la tortue) :
aff = game.add.text(0,0,0);
Pour la création du tableau possible, on le crée vide puis on initialise ses entrées à true puisqu’au début du jeu, tous les sommets sont encore visitables :
var possible = [];
for (var n in abcs){
possible[n] = true;
}Voici donc ce qui se passe lorsque la tortue arrive sur un rubis situé au sommet n :
- le sommet n devient impossible à revisiter, et est donc marqué tel dans le tableau possible ;
- La suite dépend du fait qu’on soit revenu au départ (lieu==0) ou non ;
- Si on n’est pas de retour au départ, c’est qu’il y a un rubis (un sprite dans gemmes[lieu]) ; on le détruit en lui envoyant le message destroy ;
- On incrémente (« ++ ») la variable richesse puisque la tortue récolte un rubis de plus ;
- on met à jour le texte dans le jeu, en réaffirmant que le texte de la variable aff doit être égal au contenu de la variable richesse ;
- On remplace le sprite qui était dans gemmes[lieu] par un nouveau sprite de type « bouche » ;
- on centre la bouche en mettant son point d’ancrage à 0,5 ;
- on redimensionne la bouche en lui appliquant une homothétie de rapport 0,3 ;
- Sinon, c’est que la tortue est de retour au point de départ (lieu==0) ; dans ce cas :
- Elle est revenue au point de départ alors qu’elle n’a le droit de le faire qu’une fois, donc désormais le point de départ aussi est marqué comme impossible ;
- Si à ce moment elle a ramené 19 rubis, le jeu est terminé et l’affichage « gagné » le confirme.
- Dans tous les cas on ne peut plus jouer : La tortue ne bougera plus.
En JavaScript cela s’écrit :
function manger(){
possible[lieu] = false;
if (lieu>0) {
gemmes[lieu].destroy();
richesse++;
aff.text = richesse;
gemmes[lieu] = game.add.sprite(chemin.nodes[lieu].x,chemin.nodes[lieu].y,"bouche");
gemmes[lieu].anchor.setTo(0.5);
gemmes[lieu].scale.setTo(0.3);
} else {
possible[0] = false;
if (richesse == 19) { alert("gagné")}
}
}Cette fonction, on l’a vue, est appelée à chaque fois que la tortue termine une promenade le long d’une arête. Le moteur du jeu est donc concentré dans cette promenade (voir l’onglet « analyse du graphe » pour sa description). En fait, cette promenade se fait entre deux sommets : Celui où est la tortue, et celui où va la tortue. Cette promenade ne peut se faire que
- s’il y a une arête entre les deux points ;
- si l’arrivée est encore visitable par la tortue (il n’y a pas de bouche ouverte)
La vérification se fait dans une fonction essai dépendant d’un acteur (le jeu) et d’une souris (là où on a cliqué) :
function essai(acteur,souris) {
var oussamissava = prochain(souris.x, souris.y);
if(liaison(lieu, oussamissava) && possible[oussamissava]){
promenade(chemin.nodes[lieu],chemin.nodes[oussamissava]);
lieu = oussamissava;
}
} Cette fonction commence par calculer les coordonnées du sommet le plus proche de là où on a cliqué (oussamissava est le numéro de ce sommet) ; puis déclenche la promenade si les conditions décrites ci-dessus sont respectées, et enfin met à jour la variable lieu puisque dans ce cas, la tortue a bougé.
Cette fonction est appelée à chaque fois qu’un clic sur le jeu a lieu, et il est donc nécessaire de rendre le jeu cliquable (dans la fonction create) :
var fond = game.add.tileSprite(0,0,game.width,game.height,"fond");
fond.inputEnabled=true;
fond.events.onInputDown.add(essai,this);C’est tout ! Le jeu fonctionne !
Récapitulatif
Pour créer le jeu Phaser, on donne ses dimensions, et les noms des fonctions preload (à effectuer avant de créer les objets du jeu) et create (la création du jeu : Placement des objets dans le jeu ; ah tiens, un micromonde !) :
var game = new Phaser.Game(480,480,Phaser.AUTO,'content',{preload: preload, create: create,update:update});La fonction preload est celle-ci :
function preload(){
game.load.image("fond","img/ocean.jpg");
game.load.spritesheet("tortue","img/tortue.png",100,121,8);
game.load.spritesheet("bouche","img/gaignpi.png");
game.load.spritesheet("rubis","img/rubygem.png");
}Et la fonction create est celle-ci :
function create(){
var fond = game.add.tileSprite(0,0,game.width,game.height,"fond");
dessineGraphe(chemin);
aff = game.add.text(0,0,0);
turtle = game.add.sprite(240,30,"tortue");
turtle.z = 3;
turtle.anchor.setTo(0.5);
turtle.scale.setTo(0.5);
turtle.angle = 90;
var walk=turtle.animations.add("walk")
turtle.animations.play("walk",16,true);
fond.inputEnabled=true;
fond.events.onInputDown.add(essai,this);
}Ce n’est pas tout : Il y a les déclarations de variables, les fonctions manger etc. Le source complet (avec les graphes) est ici
Pour créer une variante de ce jeu, il suffit de modifier
- les coordonnées des sommets du graphe
- les définitions des arêtes du graphe
- le cas échéant, la largeur des traits
- le nombre total de rubis à ramasser
Ce qui donne lieu aux variantes ci-dessous, concernant d’autres graphes hamiltoniens. Tester si un graphe quelconque est hamiltonien est un problème assez difficile pour que la théorie du jeu soit évitée dans cet article.
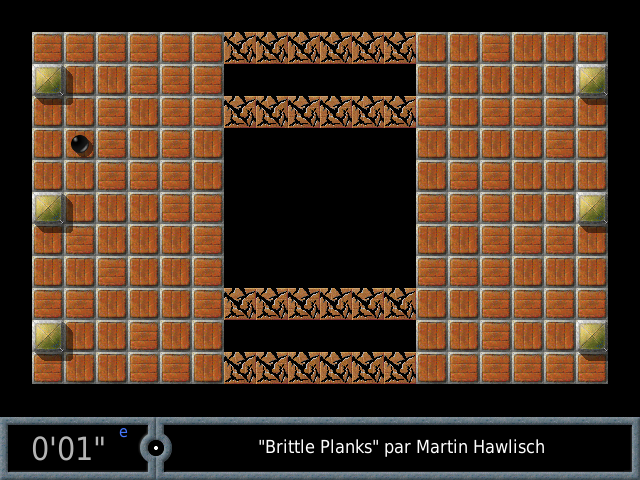
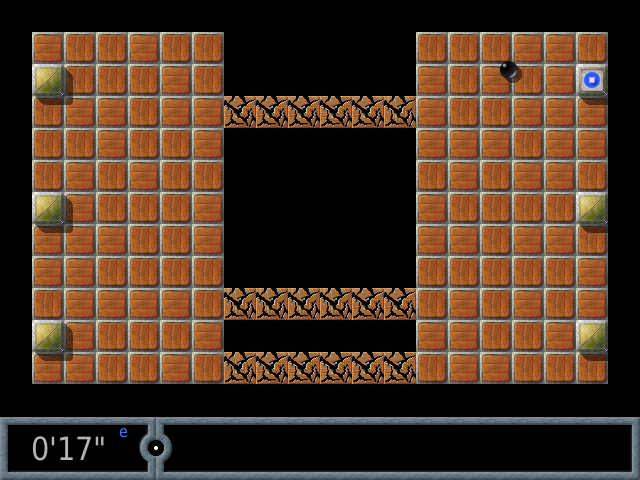
Voici les 4 jeux de type icosien sur des polyèdres réguliers, programmés en Phaser :
- Euh attendez, pourquoi seulement 4 jeux, alors qu’il y a 5 polyèdres réguliers ?
- Oui, on n’a pas fait le jeu sur un tétraèdre.
- Alors là c’est un peu l’arnaque : 5 polyèdres réguliers, 5 jeux, c’est comme ça !
- Mais c’est que ...
- Taratata ! Remboursez les 0€ que j’ai payés pour ces jeux libres et gratuits !
- Mais pour le tétraèdre, le graphe est un graphe complet à 4 sommets, sur lequel tout circuit est hamiltonien : Il est impossible de perdre !
- Ah bon alors dans ce cas le jeu sur tétraèdre est encore moins intéressant que les autres, lesquels sont seulement un peu trop faciles...
- On peut toujours considérer le jeu sur un tétraèdre comme un exercice de programmation,en fait c’est plus ludique de créer des jeux, que de les tester...
Édouard Lucas a relativement peu écrit sur ce jeu, parce qu’il lui trouvait un air de déjà-vu : Une équivalence possible se montre avec une variante du jeu de dominos :

Le jeu icosien comme variante du solitaire
C’est un de ses correspondants qui a suggéré à Lucas une variante du jeu de solitaire qui se révèle équivalente au jeu icosien :

Pour le vérifier, on peut essayer de jouer en ligne au jeu de solitaire suivant (cliquer sur l’image) :
Si on trouve ce jeu difficile, on peut s’entraîner sur la version cubique ci-dessous ; le plus dur n’est pas de trouver la solution mais de voir en quoi elle est équivalente à la recherche d’un circuit hamiltonien...
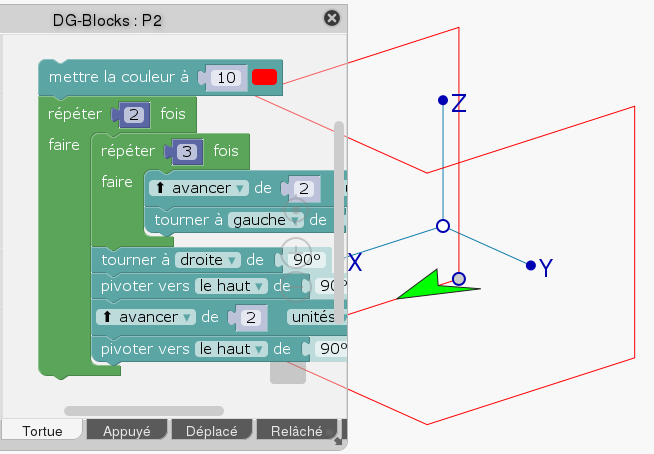
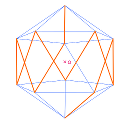
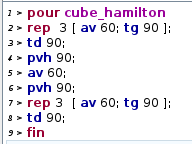
Pour la version 3D du jeu, il faut un logiciel de 3D ; mais finalement, le tracé d’un circuit hamiltonien est une affaire de tortue ... Logo ! Par exemple, dessiner un pentagone en Logo se fait avec quelque chose comme
repete 5 [ av 80 tg 72]
Ce script ne fait rien d’autre que parcourir un circuit hamiltonien sur le pentagone (puisque les 5 sommets sont parcourus et 5 des arêtes, à vrai dire les 5 seules arêtes, aussi). Pour que la tortue puisse dessiner les arêtes d’un polyèdre ou un polytope régulier sans avoir à se téléporter, il faudra donc qu’elle dessine plusieurs circuits hamiltoniens en 3D ou en 4D. On va étudier séparément le cas de la dimension 3 (avec DGPad) et celui de la dimension 4 (avec GeoTortue) ci-dessous.
Addendum : Un autre jeu basé sur les circuits hamiltoniens.
Bien avant la découverte du jeu icosien, un autre jeu était déjà pratiqué depuis des siècles, et finalement assez similaire : Le problème du cavalier. La première étude mathématique du problème date de 1759 et, par chance, a été rédigée en français. La voici assortie d’un commentaire :
| L’article d’Euler | Le commentaire | Le source du commentaire | La version d’Ed Sandifer |

























Commentaires