Préparation de la palette restreinte

Comme pour les activités précédentes, une adaptation de la palette de CaRMetal a été nécessaire. Nous avons donc mis à disposition des élèves, dans l’onglet construction que les icônes nécessaires à la construction du rectangle. Pour la deuxième partie de la séance, les icônes cercle étaient aussi présents (sauf le cercle compas).

On trouve dans l’onglet construction les icônes suivantes : point, milieu, droite, demi-droite, parallèle, perpendiculaire, segment, cercle et cercle de rayon fixe (ces deux derniers icônes serviront surtout pour la deuxième partie de la séance). Dans l’onglet test, nous avons laissé les icônes : points alignés, parallèles, perpendiculaire, point appartenant à une droite.

Présentation de l’activité de construction

Les élèves ont à leur disposition le classeur .zirs de CaRMetal dans lequel se trouvent les deux fichiers : celui pour la construction et celui du problème.
Pour cette première partie, les élèves doivent construire un rectangle (figure classique, usuelle c’est à dire connue des élèves depuis la maternelle) en utilisant le logiciel de géométrie dynamique. La consigne suivante leur est donnée à l’oral : « Vous devez construire un rectangle en utilisant le logiciel. En même temps que vous construisez ce rectangle, vous devez écrire ce que vous faîtes à chaque étape de votre construction. Vous pouvez ensuite valider votre construction en utilisant le Monkey. »
On peut envisager de revoir avec les élèves les propriétés du rectangle : côtés parallèles deux à deux de même mesure, quadrilatère ayant quatre angles droits, diagonales de même longueur qui se coupent en leur milieu. Ces propriétés sont notées au tableau et restent visibles tout le long de la séance.
On laisse les élèves faire le travail sans plus d’indication si ce n’est le rappel de certains icônes. Pour les groupes d’élèves les plus rapides, on peut leur montrer comment bien achever le rectangle en repassant sur les droites avec des segments puis en cachant les droites « support de construction » avec l’outil « cacher ».
Les fiches de travail sont distribuées au début de la séance et les élèves notent les étapes de la construction au fur et à mesure de son déroulement.
Ensuite, les élèves peuvent valider leur figure en utilisant le Monkey. La figure, pour être valide doit absolument résister au mouvement.
Après cette phase de construction et de rédaction, on procédera à la mise en commun ; l’enseignant veillera à choisir des exemples de construction pertinents justes et faux afin de les soumettre à discussion : est-ce juste ? pourquoi ? qu’aurait-il fallu faire ? Quels tests peut-on utiliser pour vérifier les propriétés de la figure construite ? (Monkey, outils du test onglets)... sont des exemples des questions que l’on peut poser aux élèves.
On veillera à la qualité et à la pertinence du vocabulaire utilisé par les élèves.
A la fin de cette mise en commun, on aboutira à un programme de construction.

Les attendus

Il est fort probable que dans un premier temps les élèves reproduisent avec le logiciel ce qu’ils font sur papier (ils seront sur des démarches perceptives) : ils vont dessiner un rectangle « à main levée » en utilisant l’icône segment se basant sur le crénage des traits pour faire des segments « droits » (terme utilisé par les élèves). Mais l’utilisation du Monkey invalidera la construction. Pour ces élèves, il faudra reprendre avec eux les propriétés du rectangle.

On attend que les élèves écrivent cela (bien entendu, il existe d’autres programmes de construction justes ; ici, nous n’en donnerons qu’un seul à titre d’exemple) :
étape 1 : je crée un segment (noté ou non [AB])
étape 2 : je trace la perpendiculaire à [AB] ou au segment, passant par A
étape 3 : je trace la perpendiculaire à [AB] ou au segment, passant par B
étape 4 : je place un point C sur une des perpendiculaires tracées précédemment
étape 5 : je trace la parallèle à [AB] passant par C
étape 6 : je nomme la nouvelle intersection D
Par la suite on tracera ensuite les segments [AB], [BC], [CD] et [DA] et on cachera les droites supports pour terminer le rectangle.

Les productions erronées

Cette séance est la troisième que les élèves réalisent dans un environnement de géométrie dynamique. ce fut cependant le premier exercice de construction d’un figure pour les élèves. Cette activité qui a pu paraître simple aux premiers abords pour les élèves s’est révélée difficile.
Les premières constructions sont perceptives et donc invalidées par l’utilisation du Monkey, les élèves ayant tendance à effectuer, reproduire les gestes de la géométrie papier-crayon (gestes qui seront invalidés par l’environnement de la géométrie dynamique)
Rudy et Brice
Quand on regarde leur production avant toute utilisation de tests ou de Monkey, visuellement, la figure semble correcte.

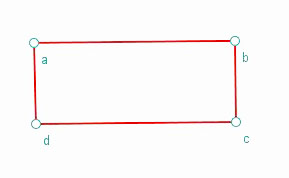
Pour ces deux élèves, on est dans une géométrie perceptive ; les caractéristiques du rectangle ne sont pas exprimées par les élèves. Le rectangle est reconnu « au jugé » d’après son apparence.
Quand on lui demande comment il peut être sûr qu’il a devant lui un rectangle, il répond que « ça a la forme d’un rectangle ».
Après l’utilisation du Monkey, ils constatent que leur rectangle ne résiste pas au déplacement (à leur grande stupeur).
Si on fait le test parallèle sur leur figure, on constate que les segments [AB] et [CD] sont parallèles. Pour le reste, il n’y pas de côtés perpendiculaires.
Lors de l’analyse de cette figure (hors présence des élèves car cela prendrait trop de temps), nous repassons en palette normale (c’est à dire que nous allons décocher l’environnement restreint) afin de pouvoir activer l’icône afficher/masquer les objets cachés. Cela va nous permettre de voir et comprendre ce que les élèves ont fait.
Voici une copie d’écran de leur travail une fois affiché les objets cachés :

Des tests ont été réalisés par les élèves montrant des objets parallèles ou perpendiculaires qui sont les droites tracées en bleue.
Les points d’intersections sont corrects mais les points a et b ont été placés sur deux autres droites coulissant sur la droite (ab).

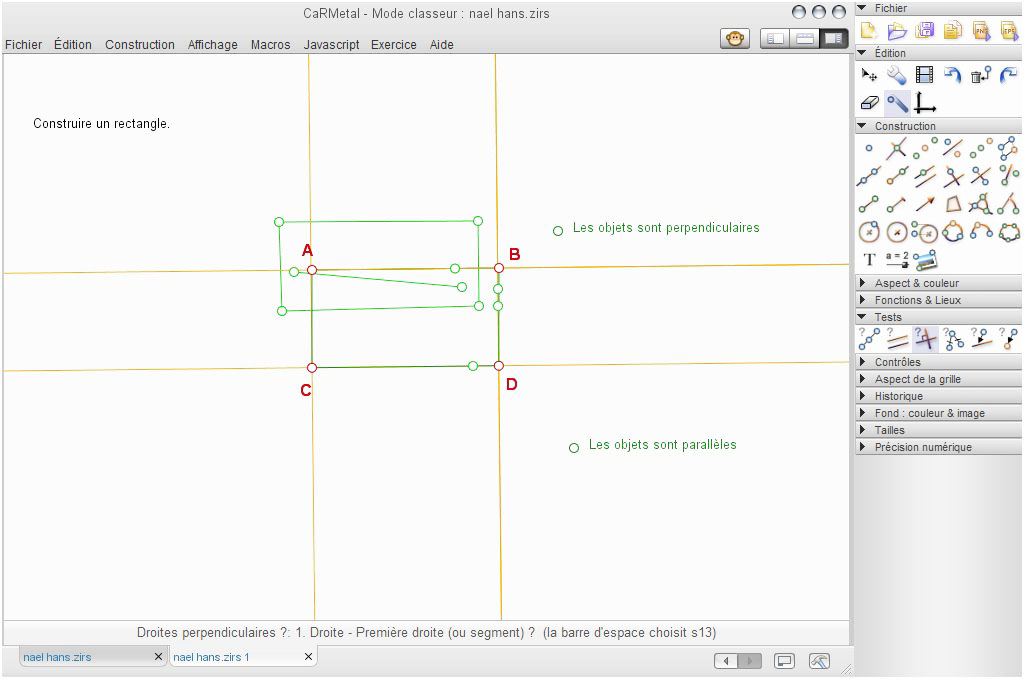
Naël et Hans
Pour une meilleure compréhension, nous avons nommé les points du rectangle construit. On peut voir sur la capture d’écran suivante que ces deux élèves ont utilisé les tests parallèle et perpendiculaire avec comme résultat que les objets sélectionnés étaient parallèles et d’autres objets étaient perpendiculaires.

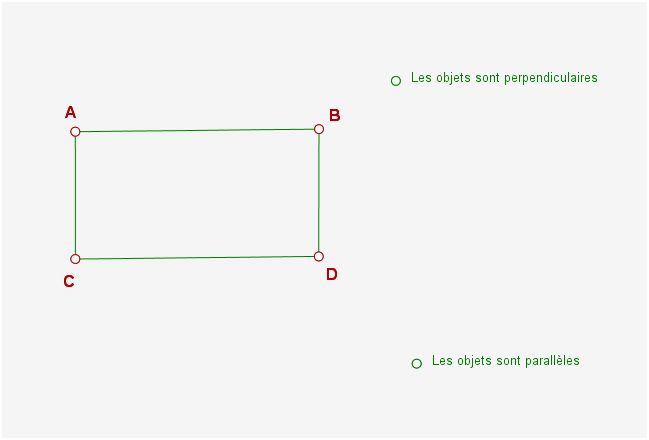
Or lorsque l’on veut valider la figure par le Monkey, on s’aperçoit que la figure construite ne résiste pas au déplacement. Les seuls côtés restant parallèles étaient les segments [AB] et [CD]. Ce qui nous a amené à repasser en environnement non restreint pour voir ce que les élèves nous avaient cachés.
L’hypothèse venait du fait qu’il avait du y avoir une précédente construction sur laquelle le test perpendiculaire a été fait. Voici ce que cela donne une fois les objets cachés affichés :

Une première figure avait été réalisée comme pour le groupe d’élèves précédent : ils avaient réalisé le rectangle en utilisant que les segments et le perceptif pour ajuster le figure.
Pour Naël et Hans, la trace écrite correspond au premier rectangle construit et qui a été caché par la suite ; voici ce qui a été écrit :
étape 1 : je mets un point
étape 2 : je trace un segment AB
étape 3 : je trace un segment BC
étape 4 : je trace un segment CD
Les élèves n’ont pas eu le temps d’écrire leur dernière phase.

Les productions justes

Félix
La figure construite par ce groupe d’élèves résiste au déplacement :

Mais voyons ce qui a été réellement fait par ces élèves en montrant les objets cachés :

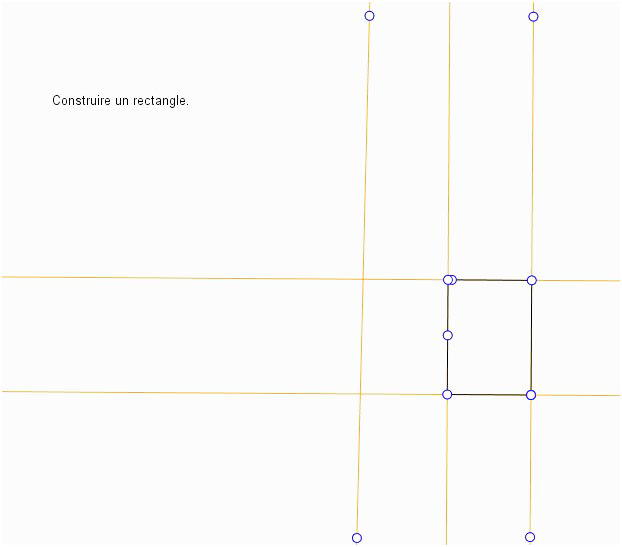
Il semblerait qu’il y ait eu plusieurs essais sur la construction des points.

Nahya, Marion et Chloé
La figure construite par ce groupe d’élèves résiste aussi au déplacement :

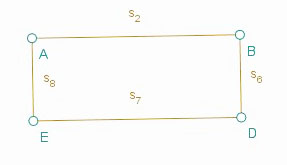
En affichant les objets cachés, on a ceci :

La construction est correcte et ces élèves ont réalisé les tests afin de s’assurer de la valider des propriétés du rectangle.
Maintenant si on regarde leur trace écrite, nous constatons que le programme de construction qu’elles ont réalisé est correcte. Voici leur production écrite :

Tom et Quentin
On peut faire les mêmes remarques que précédemment même si les tests effectués sur la figure sont moins nombreux :

Emmano et Quentin
La construction est juste et quand on observe ce qui a été fait, on a un programme de construction juste (comme nous le montre l’image ci-dessous).

Si on s’intéresse à leurs écrits, nous constatons qu’il est correct dans la démarche mais avec des « approximations dans le vocabulaire utilisé » :
voici leur retranscription :
étape 1 : je trace un segment [AB]
étape 2 : je trace une droite E perpendiculaire à [AB]
étape 3 : je trace une droite perpendiculaire à l’intersection de B
étape 4 : je trace une droite perpendiculaire aux droites E B

En ce qui concerne les autres écrits, ces derniers ont été peu utilisables.

Extraits vidéo de la séance

Premier extrait vidéo

Commentaires :
Manifestement ces élèves n’ont pas compris ce qu’est la géométrie dynamique malgré les deux séances d’appropriation du logiciel et d’instrumentation. Les élèves n’ont pas senti la différence. On constate qu’ils fonctionnent comme dans l’environnement papier-crayon. Sur le segment, au lieu de le modifier, ils l’effacent et le reconstruisent.
Les exercices d’instrumentation étaient en définitive des exercices de précision et non des exercices mettant en jeu la notion de géométrie dynamique. En visant la précision, on a perdu de vue d’autres aspects de la géométrie dynamique.

Deuxième extrait vidéo

Commentaires :
C’est le premier exercice de construction des élèves.
On constate bien l’ambiguïté qu’il y a dans la validation : alors que dans une séance en environnement papier-crayon on valide les dessins (sur écran) , en environnement informatique avec la géométrie dynamique, le Monkey fait que la construction du rectangle n’est pas correcte car la figure ne résiste pas au déplacement.
L’utilisation du Monkey permet de faire prendre conscience aux élèves de leur démarche perceptive dans la construction du rectangle.

Troisième extrait vidéo

Commentaires :
Dans cet extrait, l’élève a bien reconnu les propriétés affines de la figure (côtés parallèles deux à deux) mais pas les propriétés euclidienne (les angles droits) alors que le rectangle est une figure connu depuis le cycle I.
Cet extrait vidéo illustre un résultat bien connu des psychologues (cf.Piaget) sur le fait que les propriétés affines sont reconnues bien avant les propriétés euclidiennes. Comme ces propriétés affines sont reconnues avant, elles deviennent un outil de construction (cf. Charnay ERMEL). Les savoirs sur l’angle droit sont peut-être trop récents pour être des outils.

Quatrième extrait vidéo

Commentaires :
On constate qu’au deuxième essai, les élèves ont bien compris l’utilisation du logiciel et le sens mathématiques de la tâche à accomplir( il faut maintenir l’angle
Les élèves analysent bien leur erreur et pour cela ils utilisent l’outil droite perpendiculaire.

Conclusion

Spontanément certains élèves tracent le rectangle au jugé. La validation par le Monkey disqualifie la production de manière très claire pour les élèves. Après ce premier échec, ces derniers vont combiner les dessins au jugé et les propriétés affines de la figure et de nouveau vont utiliser le Monkey pour valider leur construction et là l’analyse de l’erreur risque d’être moins aisée du fait qu’une partie de la figure est correcte.
A la fin de cette première activité, on peut quand même dire que les élèves ont assez bien réussi la construction du rectangle.
On peut remarquer un point qui a interpellé les élèves :
Une des premières difficultés est qu’un rectangle est constitué de segments. dans un environnement papier-crayon, il est assez aisé de le réaliser à partir de segments ce qui n’est pas le cas dans environnement e la géométrie dynamique : les élèves devant construire le rectangle avec des droites supports pour les segments et notamment des droites perpendiculaires ou parallèles. Dans cet environnement, le segment [AB] et la droite (AB) sont deux objets différents. pour les élèves, le segment [AB] est inclus dans la droite. Ainsi on peut dire que les représentations et les schèmes d’actions des élèves sont perturbés.
En résumé, l’élève va rester pour résoudre un problème sur ses schèmes d’actions d l’environnement papier-crayon avec les outils qu’il a l’habitude d’utiliser et c’est seulement après la non validation par l’utilisation du Monkey qu’il va se tourner vers d’autres schèmes d’action et outils.
Autre remarque : l’écrit ; il est difficile pour la majorité des élèves d’écrire ce qu’ils font en même temps qu’ils le réalisent. En effet, les activités sur l’ordinateur sont des activités qui se réalisent en acte alors que le passage à l’écriture demande une conceptualisation (cf. Vergnaud)
La pratique de la géométrie dynamique (par l’interaction qu’elle permet avec leurs propres productions) est un moyen d’accélérer la transformation des savoirs en outils de construction.

Le problème posé aux élèves

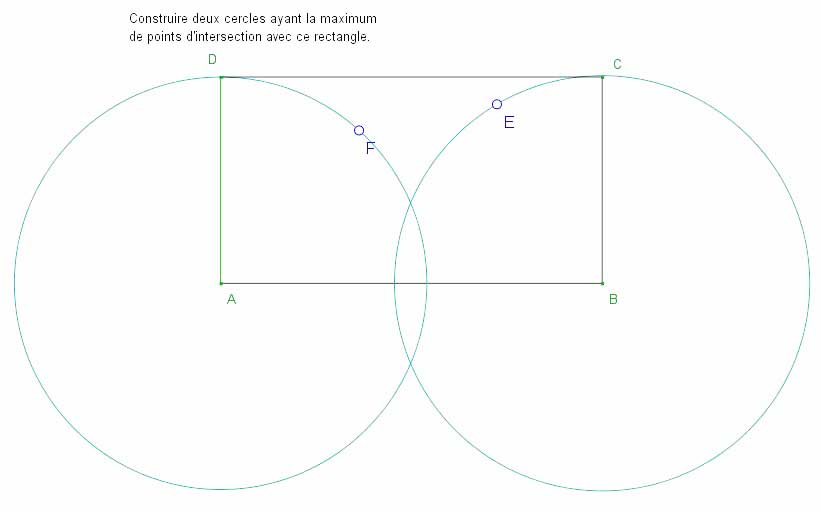
Les élèves vont sur le fichier problème du classeur de CaRMetal. Sur ce fichier est déjà tracé un rectangle dont on aura fixé les sommets.
La consigne donnée à l’orale est la suivante :
« A partir de ce rectangle, vous allez devoir construire deux cercles ayant un maximum de points d’intersection avec ce rectangle. Dans un premier temps, essayer d’estimer le nombre de points d’intersection, notez le, puis tester avec le logiciel. »
Pour ce problème, nous avons ajouter à la palette d’outils de construction, en plus des outils nécessaires à la construction du rectangle, les deux premières icônes du cercle : le cercle par centre et point et le cercle de rayon fixe afin de permettre l’apparition de procédures différentes chez les élèves.
L’utilisation de l’icône cercle « par centre et point » doit permettre aux élèves qui le choisissent d’avoir deux paramètres pour modifier le cercle : le centre et le point M (sur le cercle).
Avec l’icône "cercle de rayon fixe, les élèves n’ont qu’à gérer qu’un point supplémentaire. Et en décochant la case fixe dans l’inspecteur d’objets, ils peuvent aussi changer le rayon du cercle et l’ajuster comme ils le veulent.
Dans l’environnement papier-crayon et dans une perspective d’investigation, cette séance aurait été délicate à mettre en œuvre car une fois les cercles dessinés, les élèves ne pourraient plus agir sur eux. Avec la géométrie dynamique, les rayons des cercles peuvent être ajustés en affinant à la souris les positions des centres des cercles ou le rayon. C’est bien là la différence entre l’environnement papier-crayon et l’environnement de la géométrie dynamique.
La solution
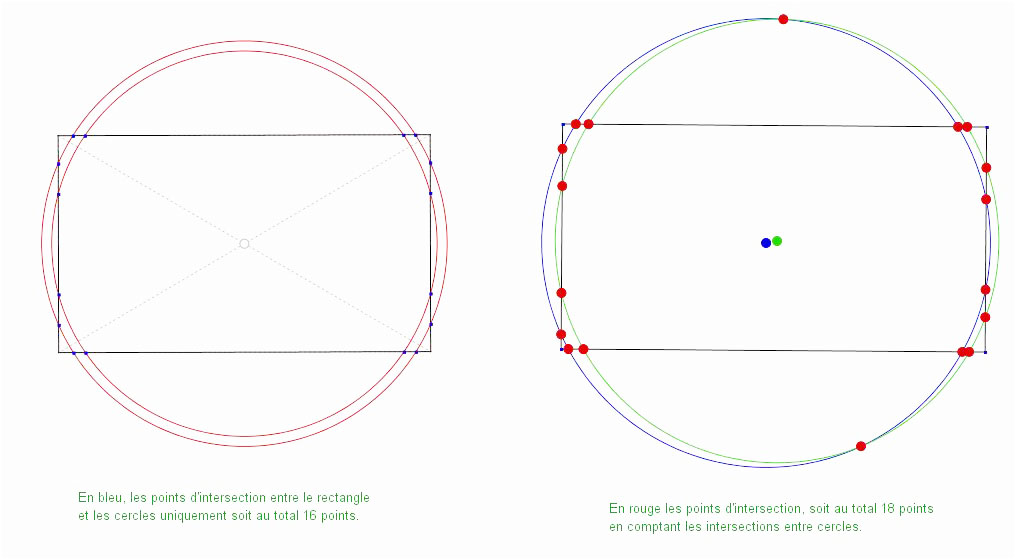
Si on ne compte pas le nombre d’intersections entre les deux cercles, on obtient seize points comme nous le montre l’image ci-dessous :

Pour avoir les dix-huit points d’intersection, il faut décaler les centres des cercles, contrairement au premier cas où les centres sont le milieu du rectangle soit l’intersection des diagonales du rectangle.
Lors de la mise en commun, on veillera à demander aux élèves de justifier ce nombre d’intersections : on attend qu’ils disent qu’il ne peut y avoir que deux points d’intersection entre une droite et un cercle et comme le rectangle a quatre cotés, on aboutit en tout à huit intersections pour un cercle soit au total seize points avec les deux cercles.

Ce que l’on attend des élèves

Dans un premier temps, on s’attend à ce que les élèves placent le centre des cercles sur deux des sommets du rectangle. Si c’est le cas, il faudra leur faire compter le nombre d’intersections et leur dire qu’il y en a plus que ce qu’ils ont trouvé.
Ils peuvent aussi placer le centre des cercles approximativement au milieu du rectangle et ajuster le rayon du cercle en déplaçant le centre, « réglant » le rayon (dans l’inspecteur d’objet) ou en déplaçant le cercle s’ils ont utilisé l’icône cercle de rayon fixe, soit en « tirant » sur le cercle ou aussi en déplaçant le centre s’ils ont utilisé l’icône cercle.

Les productions des élèves

Des cercles dont les centres sont sur les sommets du rectangle
Quelques productions ont montré que des élèves avaient placé le centre d’un des cercles sur un des sommets du rectangle et dont le rayon était la largeur du rectangle comme on peut le voir ci-dessous :

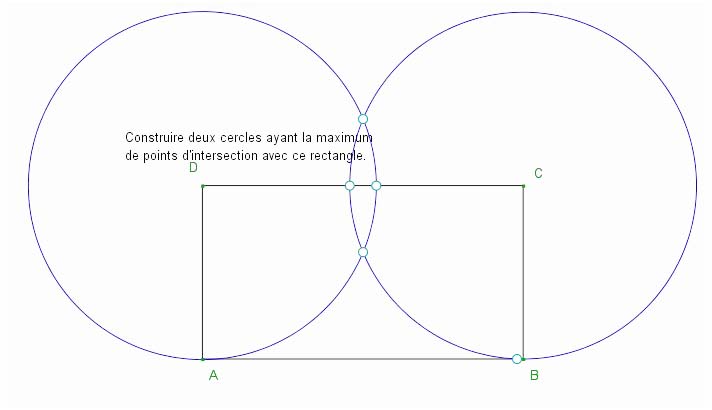
Des cercles dont le centre est au milieu du rectangle
D’autres productions ont montré que les élèves avaient placé à vue d’œil le centre des deux cercles au milieu du rectangle. Un seul groupe s’est servi de l’intersection des diagonales pour trouver le milieu.
Seules les deux dernières sont justes :

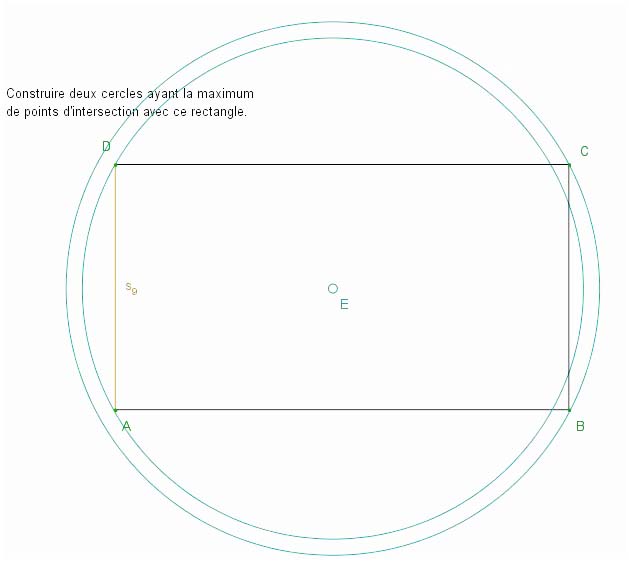
Bilan
Dans cette séance, il n’y avait ni objets complexes ni de propriétés caractéristiques. Les élèves devaient simplement mettre en place une démarche permettant par la simple narration de recherche d’arriver à avoir une démonstration mathématique correcte. L’intérêt d’utiliser un logiciel dans ce type d’exercice est de permettre d’ajuster les objets (ici les cercles) pour essayer d’avoir le plus d’intersections possibles. On peut bien entendu ajuster le rectangle ce qu’a priori les élèves n’ont pas fait car ce fut le premier objet construit et qu’il n’est pas habituel pour eux de le modifier.
Cette partie de la séance n’a pas été à la hauteur de nos attentes.
En effet, une fois les cercles placés, les élèves n’ont pas essayé de les déplacer pour les ajuster sur le rectangle. Cela peut s’expliquer par le fait qu’il n’y a pas eu auparavant de séance d’instrumentation sur les cercles, c’était la première fois qu’ils les utilisaient.
Il est donc intéressant de commencer à faire de la géométrie dynamique tôt de manière à ce que les élèves s’approprient mieux les concepts en jeu.

Pour les groupes ayant trouvé les seize points d’intersection, les élèves n’ont pas su donner une justification de leur résultat. Leur réponse était « on la fait un peu au hasard ». Ce problème n’est pas une activité habituelle pour les élèves qui sont plutôt habitués à construire et donc ces derniers ne sont pas rentrés dans une phase de recherche d’investigation, où ils pouvaient essayer, ajuster etc. Dans cette activité, ils ont travaillé comme dans un environnement papier-crayon : une fois la construction des cercles faites, ils se sont contentés de la réponse qu’ils voyaient à l’écran.