Le logiciel de géométrie dynamique DGPad est un logiciel pour tablettes, mais qui fonctionne aussi sur ordinateur. Au moment où cet article est écrit, c’est une webapp, donc qui ne fonctionne qu’en ligne. Elle est néanmoins destinée à devenir rapidement une application autonome après les premiers retours d’utilisateurs.
Quelques précisions techniques
Sous Android il faut utiliser Firefox, sous iOS, Chrome ou Safari.
Sur ordinateur, on peut glisser les fichiers .txt proposés au téléchargement dans cet article, sur la fenêtre principale de l’application (du navigateur). Sur tablette, soit on dispose d’un système de gestion de fichiers, soit on utilise un nuage comme DropBox ou autres.
Le fonctionnement des outils contextuels, fait pour tablettes, est suffisamment original pour fortement conseiller de regarder au moins les premières vidéos de présentation sur le site de DGPad avant de se servir de l’application.
Un tour d’horizon assez large du logiciel, une première analyse de ses choix et une présentation de ses possibilités techniques sera proposée de manière structurée dans le numéro 35 de MatheMATICE (mai 2013).
La problématique de l’article
Mais, en attendant, les auteurs de cet article souhaitaient montrer quelques unes de ses possibilités dans le cadre de cette question : comment pourrait-on faire des tableaux de fils dynamiques avec ce logiciel naissant qui, certes, a des macros, mais n’a pas encore d’expressions algébriques disponibles directement dans l’interface utilisateur ?
On suppose que le lecteur a déjà joué à cela, soit par exemple avec les séquences de Geogebra, soit encore avec les CaRScripts de CaRMetal (comme on l’a déjà fait ici - premier onglet)
C’est bien entendu un prétexte pour parler des scripts (naturellement disponibles dans DGPad puisque le logiciel est entièrement écrit en JavaScript) et même de l’utilisation de fonctions récursives ...
En toile de fond [1] c’est aussi une illustration de nos capacités, comme enseignants, à adapter nos techniques usuelles (nos schèmes d’action et nos réflexes culturels) à un nouvel environnement, qui a - temporairement - d’autres contraintes que celles que l’on connaît d’habitude et pour lequel nos pratiques spontanées ne peuvent s’appliquer.
Comme les figures s’exportent très facilement, elles seront - pas toujours mais souvent - dans le corps du texte.
• Une technique de lieu de segments, dans laquelle on ne fait que donner la main au logiciel.
• Une méthode utilisant le nommage de points : c’est la première réellement efficace, mais assez subtile à mettre en œuvre. Son algorithme mérite d’être regardé de près et peut être utilisé dans différentes situations (comme en ISN probablement).
• Une méthode qui veut éviter le nommage des points (d’où la récursivité).
• Un retour à la géométrie, en construisant des graduations : plus flexible que les deux précédentes, mais plus gourmande en points.
1. Comme lieu
Tableaux de fils comme lieu de segments.
Ce premier onglet est aussi l’occasion de montrer rapidement le fonctionnement du logiciel aux personnes qui ne l’ont pas encore utilisé.
Tracé des deux segments
On construit trois points, puis on les joint par deux segments. Pour cela, on sélectionne un des points :
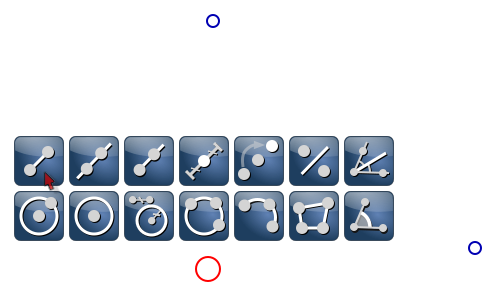
On constate que la palette d’outils qui apparaît, correspond à tout ce qu’on peut faire subir à ce point ; on choisit le segment. Mais on ne doit pas relâcher l’outil sinon on aurait la création d’un autre point au hasard : Au contraire, on fait glisser l’outil de construction
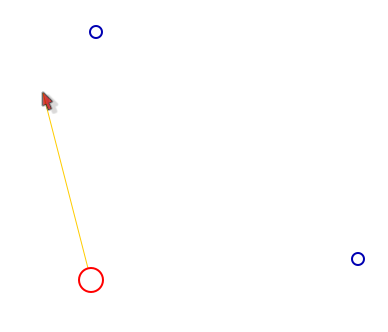
jusqu’à l’autre extrémité :
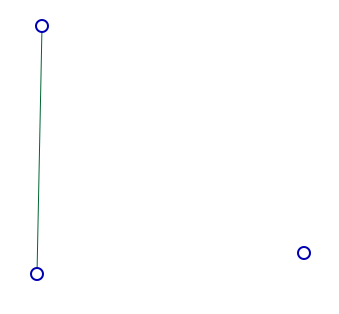
On fait pareil pour construire l’autre segment (horizontal).
Construction d’un point sur segment
Pour attacher un point au segment, on sélectionne celui-ci :
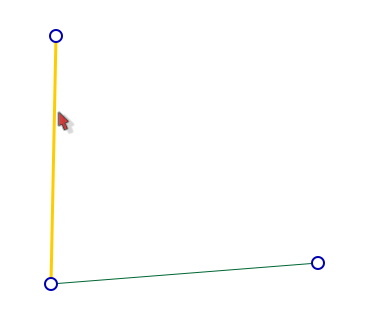
On choisit alors le premier outil de la palette (le point) :

Report de longueur
On veut reporter la longueur allant de l’extrémité haute du segment au point mobile, depuis l’extrémité basse du segment. Le point de départ de cette construction étant l’extrémité haute du segment, on le sélectionne, et là, l’outil de report de longueur :
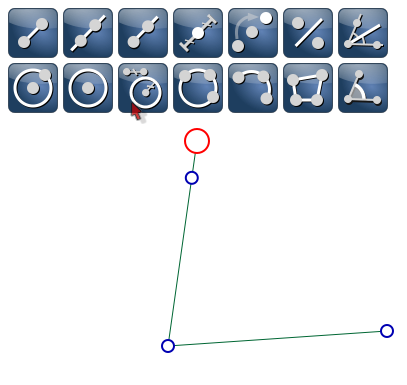
On fait glisser cet outil vers l’autre point définissant la longueur à reporter :
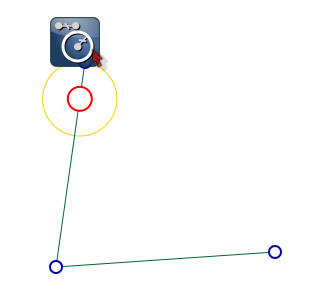
puis on fait glisser le même outil vers l’origine du repère [2] :
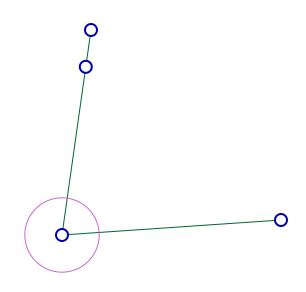
Tendre le fil
On veut que la longueur reportée soit sur le segment horizontal : Pour cela on construit l’intersection du cercle juste construit et dudit segment ; on le fait par sélection simultanée des deux objets :

Puis on choisit l’outil « point » :
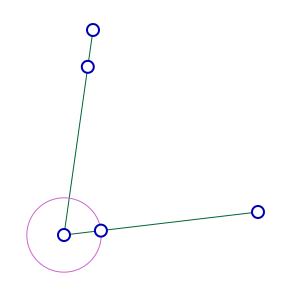
Enfin on joint ce point au point mobile par un segment :

Figure finale
Comme le segment qu’on vient de construire dépend d’un point sur segment, il possède un nouvel outil « lieu » :

Il suffit alors d’activer cet outil pour finir la figure.
La voici : On peut vérifier en bougeant l’un des trois points, qu’on a toujours une conique (en fait une parabole) :
On voit que l’enveloppe tracée est celle de droites, pas de segments, et qu’on n’a aucun contrôle sur le nombre de fils tendus. Donc on va essayer, dans les onglets suivants, de faire un tableau de fils bornés.
2. Par nommage de points
Algorithme de nommage séquentiel des points obtenus par milieux itérés
Principe : Comme on ne dispose pas de possibilité de traitement d’un pas de subdivision d’un segment, une méthode consiste à utiliser des milieux successifs. Dans cette approche, on se limite à des partages des segments en un nombre qui est une puissance de 2, en pratique, 16 ou 32.
Or, si on envisage de partager un segment en 16, le premier milieu sera le 8° point, puis les suivants les 4° et 12° ... et il faut donc les nommer en conséquence.
L’algorithme consiste à relier le point A1 au point B15, le point A2 au point B14 etc. Il faut donc que les points A1, A2 etc soient alignés dans cet ordre, ainsi que les points B1 à B16. Les points A1, A2 ... A15 seront construits par milieux, et les points O (qui remplace à la fois A0 et B0), A16 et B16 seront construits d’avance sur la figure, ainsi que les segments [OA16] et [OB16]
Construction pré-JavaScript
On construit donc dans DGPad, et on renomme, les objets en question :
Puis on exporte la figure en choisissant le mode texte :
Enfin on sauvegarde le résultat sous le nom tableau_fils.txt [5]. La suite des opérations se fera dans un éditeur de texte [6], sous la forme d’un programme JavaScript à ajouter dans le fichier obtenu.
Pour charger un fichier, on clique sur l’icône représentant une flèche sortant d’un nuage (car DGPad est basé sur le Cloud computing, et tout fichier est considéré comme placé sur le Cloud), et on sélectionne le fichier tableau_fils.txt avec l’outil filepicker.io qui apparaît alors.
Algorithme de tracé et nommage des points
Les points étant définis comme des milieux, il est nécessaire avant de construire l’un d’entre eux, que les extrémités du segment dont il est le milieu soient préalablement construites. La relation « est milieu de » est représentée par un arbre binaire construit en profondeur mais dont les sommets sont nommés en largeur. Le meilleur moyen de construire la double boucle qui réalise cela, est de commencer par la fin : Les derniers milieux construits seront A1, A3, A5 etc parce que les milieux d’indice pair auront tous été déjà construits. On les parcourra donc par pas de 2, en commençant par 1. Au stade précédent, on construira A2, A6, A10 et A14 parce que les autres milieux auront déjà été construits auparavant : Par pas de 4, en commençant par le premier d’entre eux.
Donc le pas est une suite géométrique de raison 1/2, de premier terme 16. Et dans cette boucle sur le pas, les points sont parcourus pas par pas, en commençant par la moitié du pas :
for(pas=16; pas>1; pas/=2){
for(n=pas/2; n<16; n+=pas){
a=n-pas/2;
if (a==0) {a="O"} else {a="A"+a;}
b=n+pas/2;
b="A"+b;
MidPoint("A"+n,a,b);
}
}Diverses additions
Dans la seconde ligne « for », n+=pas additionne le pas à la valeur courante de n ; les créations des variables a et b font de même, en soustrayant ou additionnant la moitié du pas à n. Mais dans le test et dans les deux dernières affectations, l’addition désigne la concaténation entre chaînes de caractères : JavaScript convertit automatiquement les nombres en texte parce que le premier terme de l’addition n’est visiblement pas un nombre (il est entre guillemets) et donc le second est censé être lui aussi traité comme du texte. C’est ainsi que se fait le nommage automatique des points.
Le premier point définissant le premier milieu ne s’appelant pas A0 mais 0, il a fallu ajouter un test pour régler ce cas.
Une boucle similaire permet de construire et nommer les points B1, B2, B3 etc. Chaque fois, au fur et à mesure, on met h:1 dans leur style pour les cacher.
Tendre les fils
Maintenant ça devient facile : On joint le point A15 au point B1, le point A14 au point B2, etc. Donc on joint le point A(16-n) au point Bn dans une boucle sur n :
for(n=1; n<16; n++){
Segment("A"+(16-n),"B"+n);
}Le tableau de fils ainsi construit est bien dynamique, comme on peut le vérifier en bougeant un des trois points :
3. Par récursivité
Utiliser la récursivité pour ne pas nommer les points
En terme de modification de nos schèmes d’action, l’onglet précédent, avec son algorithme sur l’arbre des milieux parcouru en profondeur dont les sommets sont nommés en largeur, nous avons été bien servis.
Mais c’est aussi un très bon plat, et dans un cours d’algorithmique c’est même un plat de résistance qui peut être resservi, au moins pour analyse de ce qu’il fait ... et ce pourrait être l’occasion de présenter aussi un logiciel de géométrie dynamique à l’interface tactile innovante ...
Le principe
Dans cet onglet, on se propose d’observer que, puisque le meilleur moyen de parcourir un arbre en profondeur est de le faire récursivement, la récursivité permet de simplifier considérablement le script ; cerise sur le gâteau (celui qui vient juste après le plat de résistance), l’algorithme récursif suivant permet également de se passer du parcours en largeur (du nommage des points).
L’algorithme de partage par les milieux successifs peut être perçu autrement que dans « la recherche de la largeur », il est même essentiellement récursif :
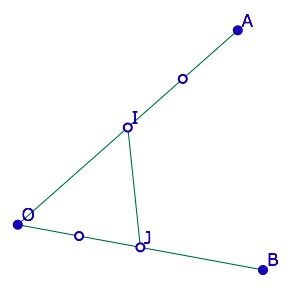
Étant donnés deux segments [OA] et [OB],
• on prend les milieux, I et J
• on applique la démarche, de manière récursive, sur [IA] et [OJ], puis sur [OI] et [JB].
On voit que la fonction récursive doit tenir compte de quatre points initiaux et non pas trois. Elle est très simple à écrire, il suffit de traduire en JavaScript ce qui précède :
function fils(a1,a2,b1,b2,k){
var m1=MidPoint(a1,a2); STL(m1,"h:1");var n1=MidPoint(b1,b2);
STL(n1,"h:1");
Segment(m1,n1);
if (k>0) {fils(m1,a2,b1,n1,k-1); fils(a1,m1,n1,b2,k-1);}
}
fils(O,A,O,B,4);Et pour trois points on applique la fonction avec deux points confondus, comme ci-dessus, ce qui donne cette figure pour un partage des segments en 32 (copie d’écran) :
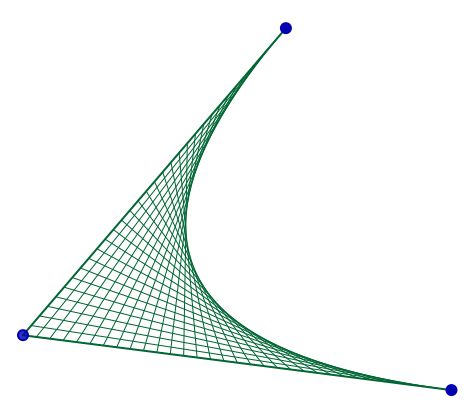
Applications immédiates
Ceci étant fait, on peut enrichir la fonction fil d’une couleur, et l’appliquer à des figures régulières comme dans ces exemples (manipulables à la souris ou au doigt).
D’autres exemples sont proposés en téléchargement en fin d’article comme celui-ci (copie d’écran) :

Et, toujours sans expression, de manière uniquement géométrique, on peut même ajouter un curseur : il fait tourner la construction intérieure bleue dans la plus grande, recyclage géométrique de ce qui est fait, de manière analytique dans cet article à l’onglet « fun » (toujours en copie d’écran) :
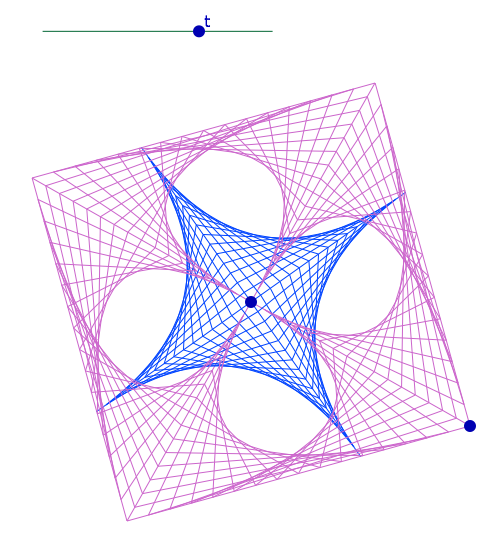
Utilisation des figures en téléchargement
Quand on charge des figures comme celles-ci, dans la version disponible au moment de la rédaction de cet article, on ne voit pas la figure se construire peu à peu - comme ce serait le cas avec des CarScripts - mais seulement à la fin de l’exécution du script, ce qui peut prendre quelques secondes.
4. Avec la géométrie
Retour à une construction plus classique
Avec Thalès, on peut subdiviser un segment en autant de subdivisions qu’on veut, ce qui permet de faire des tableaux de fils classiques à 10 points au lieu des puissances de 2 nécessaires dans les onglets précédents :
Le début est le même que dans l’onglet 2, sauf que les extrémités des segments ne s’appellent plus A16 et B16, mais A10 et B10. DGPad a nommé automatiquement S1 et S2 les deux segments ; on en aura besoin plus bas pour les intersections.
Graduation auxiliaire
On crée une graduation par des symétries centrales itérées ; le début de la graduation est O, le point suivant s’appelle C1, et C2 est défini comme symétrique de O par rapport à C1 ; ensuite, le point Cn est le symétrique de C(n-2) par rapport à C(n-1) :

Projection des graduations sur [OA10]
Ensuite, on joint le point C10 au point A10 par une droite, et les parallèles à cette droite par les points Cn coupent le segment S1 en les points An :
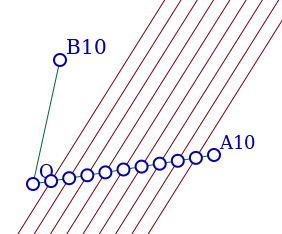
Ces points A1, A2, A3 etc sont cachés, ainsi que les parallèles, pour laisser voir le tableau de fils :

Projection des graduations sur [OB10]
On fait pareil, avec les mêmes points auxiliaires Cn, pour construire les points Bn :

Tendre les fils
Comme précédemment :

Et hop : Un tableau de fils dynamique à 10 fils :


Commentaires