Un réseau (géométrie) du plan est un nuage de points (théoriquement infini) de la forme mu+nv, où u et v ne sont pas colinéaires et m et n prennent toutes les valeurs entières possibles. En dimension 3, les réseaux sont utilisés en cristallographie, mais en dimension 2, ils engendrent des pavages, les pavés étant ici les domaines de Voronoï des points du réseau. La classification des réseau de Bravais donne les trois domaines de Voronoï possibles pavant le plan :

1) Famille cristalline monoclinique

Un cas typique est celui où u=(40,0) et v=(-10,30). Les entiers m et n bouclent d’un nombre négatif à son opposé pour couvrir toute la fenêtre.

Voici le script :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40-n*10,240+n*30]
dessineVoronoi nuage, 'magenta', 0.5

En général, le domaine de Voronoï d’un réseau plan est donc formé d’hexagones :

On ne peut s’empêcher de trouver une certaine ressemblance avec une pelure d’oignon vue au microscope :

Ceci n’a rien de surprenant si on pense que pour grandir, les cellules d’oignon cherchent à occuper tout l’espace qui leur est disponible. Des cellules de Voronoï devraient donc apparaître si les cellules d’oignon poussent en même temps.

L’azurite cristallise dans ce système.

2) Famille cristalline orthorhombique

Dans le cas particulier où l’angle est droit, les cellules sont des rectangles. Voici le script :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40,240+n*30]
dessineVoronoi nuage, 'blue', 0.5

Les hexagones sont devenus des rectangles :

Le soufre cristallise dans ce système.

3) Famille cristalline tétragonale

Ce cas particulier du précédent est celui des entiers de Gauss : Les cellules sont carrées. Le script est le suivant :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40,240+n*40]
dessineVoronoi nuage, 'blue', 0.5

Tiens, on dirait le pavage de ma cuisine :

La pyrite cristallise dans ce système.

4) Famille cristalline hexagonale

Un cas particulier important du premier cas (général) est celui où les vecteurs u et v font un angle de 60° et ont la même norme. Dans ce cas les cellules sont des hexagones.

Voici la recette du nid d’abeilles en CoffeeScript :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40+n*20,240+n*20*racine(3)]
dessineVoronoi nuage, 'brown', 0.5

Le résultat :

La couleur de miel a été choisie pour montrer la ressemblance avec les insectes les plus voronoïdiens qui soient :

Le béryl cristallise dans le système hexagonal.

On peut ajouter des variables aléatoires à l’abscisse et à l’ordonnée pour donner un aspect plus naturel au diagramme de Voronoï. Par exemple, avec la structure en nid d’abeilles perturbée :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40+n*20-10*alea()+10*alea(),240+n*20*racine(3)-10*alea()+10*alea()]
dessineVoronoi nuage, 'brown', 0.5

La couleur marron évoque plus des plaques de boue séchées :

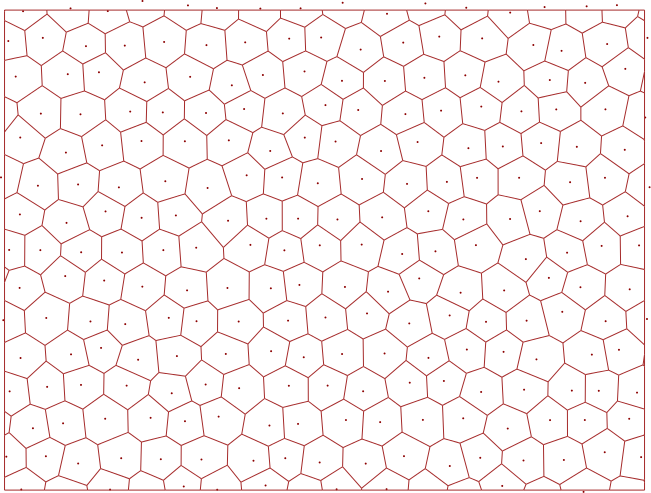
Ceci n’a rien d’étonnant, puisque la forme que prennent les croûtes de boue ou de peinture en séchant est la conséquence de cellules de Benard :

Avec le réseau carré perturbé, on obtient des écailles de serpent :

nuage = []
for m in [-20..20]
    for n in [-10..10]
        nuage.push [320+m*40-10*alea()+10*alea(),240+n*40-10*alea()+10*alea()]
dessineVoronoi nuage, 'blue', 0.5

Une vraie peau de serpent pour comparer :

Finalement, autant rendre les coordonnées des points complètement aléatoires, pour commencer uniformes dans la fenêtre :

nuage = []
for n in [1..200]
    nuage.push [640*alea(),480*alea()]
dessineVoronoi nuage, 'red', 1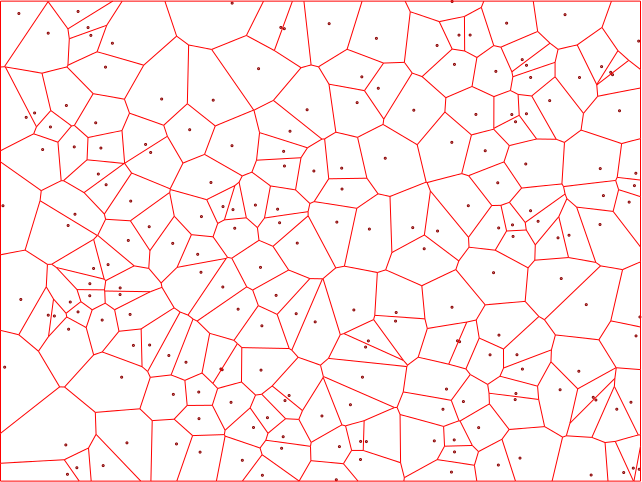

Pour continuer, gaussiens centrés sur (320,240) :

nuage = []
for n in [1..50]
    T = alea()*2*pi
    R = -80*ln(alea())
    nuage.push [320+R*cos(T),240+R*sin(T)]
dessineVoronoi nuage, 'orange', 1

Enfin, on dispose des points aléatoirement dans un anneau de rayon intérieur 160 et de rayon extérieur 200 :

nuage = []
for n in [1..80]
    T = alea()*2*pi
    R = 160+40*alea()
    nuage.push [320+R*cos(T),240+R*sin(T)]
dessineVoronoi nuage, 'cyan', 1

Le résultat :

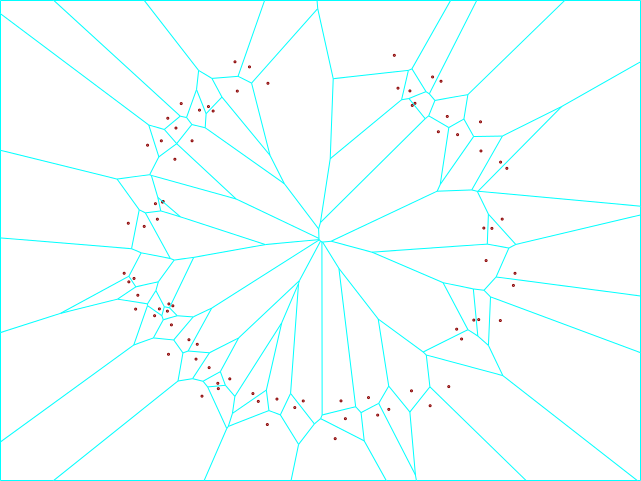
La ressemblance avec une coupe de minéral vue au microscope, est intéressante :

Un bon moyen pour avoir des diagrammes de Voronoï équilibrés, c’est de s’arranger pour que près de chaque point, se trouvent d’autres points. Ce qui se passe lorsque les points sont sur une spirale.

Un premier exemple est ce script :

nuage = []
R = 20
for n in [1..50]
    T = n*1.2
    R *=1.05
    nuage.push [320+R*cos(T),240+R*sin(T)]
dessineVoronoi nuage, 'darkGreen', 0.5

Le résultat :

Un autre exemple (spirale logarithmique) :

nuage = []
R = 20
for n in [1..200]
    T = n*0.4
    R *=1.025
    nuage.push [320+R*cos(T),240+R*sin(T)]
dessineVoronoi nuage, 'darkGreen', 0.5

Le résultat :

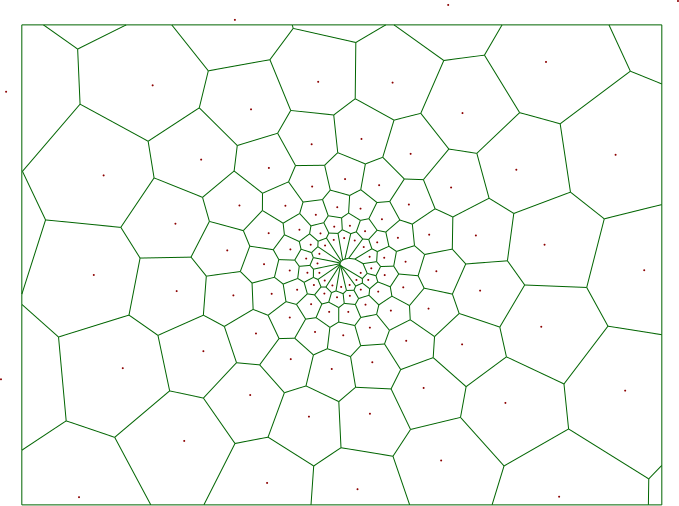
Il ressemble à la texture du fruit à pain :

Et bien entendu, le tournesol, bien connu des lecteurs de ce site :

nuage = []
for n in [1..500]
    T = 137.5*n
    R = racine(n)*10
    nuage.push [320+R*cosinus(T),240+R*sinus(T)]
dessineVoronoi nuage, 'darkGreen', 0.5

Et le vrai, pour comparer :

Les ensembles de Julia donnent parfois aussi des diagrammes de Voronoï intéressants :

Avec 0,285+0,013i

c=new Complexe 0.285,0.013
z = new Complexe 0
nuage = []
for n in [1..100]
    z = (z.fois z).plus c
    nuage.push [320+100*z.Re,240+100*z.Im]
dessineVoronoi nuage

On itère la fonction z²+c avec c=0,285+0,013i, et à chaque fois, on ajoute au nuage le point d’affixe z, correctement redimensionné.

Le résultat :

Le petit bonhomme de pain d’épices

Le script :

nuage = []
P=[0.1,-0.2]
for n in [1..200]
    P = [1-P[1]+abs(P[0]),P[0]]
    nuage.push [200+100*P[0],100+100*P[1]]
dessineVoronoi nuage, 'darkOrange', 0.5

Le dessin obtenu :

L’attracteur de Hénon

Le script produisant ce célèbre attracteur :

nuage = []
P=[0.1,-0.2]
for n in [1..200]
    P = [1-1.4*carré(P[0])+P[1],0.3*P[0]]
    nuage.push [320+200*P[0],240+300*P[1]]
dessineVoronoi nuage, 'darkMagenta', 0.5

Et son diagramme de Voronoï :

Suite aux travaux de Michel Mendès France en théorie des nombres, Pierre-Marc Mazat a dessiné dans mathemaTICE des suites de points groupés en spirale. Voici la suite de ses travaux, avec les diagrammes de Voronoï de ces nuages de points, sans les segments qui les joignaient pour montrer l’ordre de leur construction.

Avec la suite ln(n)⁴

Le cadrage adéquat est celui-ci :

f = (n) -> puissance(ln(n),4)
nuage = []
P = [50,50]
for n in [1..400]
    t=2*pi*f(n)
    P = [P[0]+20*cos(t),P[1]+20*sin(t)]
    nuage.push P
dessineVoronoi nuage, "blue", 0.5

Le diagramme de Voronoï obtenu :

Avec la suite n^1,5

Le script :

f = (n) -> puissance(n,1.5)
nuage = []
P = [100,100]
for n in [1..200]
    t=2*pi*f(n)
    P = [P[0]+20*cos(t),P[1]+20*sin(t)]
    nuage.push P
dessineVoronoi nuage, "blue", 0.5

Le diagramme de Voronoï obtenu :

Avec la suite n³/1013

Le script :

f = (n) -> n*n*n/1013
nuage = []
P = [320,100]
for n in [1..400]
    t=2*pi*f(n)
    P = [P[0]+20*cos(t),P[1]+20*sin(t)]
    nuage.push P
dessineVoronoi nuage, "blue", 0.5

Le diagramme obtenu :

Avec la suite n²/321

Le script :

f = (n) -> n*n/321
nuage = []
P = [0,240]
for n in [1..600]
    t=2*pi*f(n)
    P = [P[0]+20*cos(t),P[1]+20*sin(t)]
    nuage.push P
dessineVoronoi nuage, "blue", 0.5

Le diagramme obtenu est périodique :

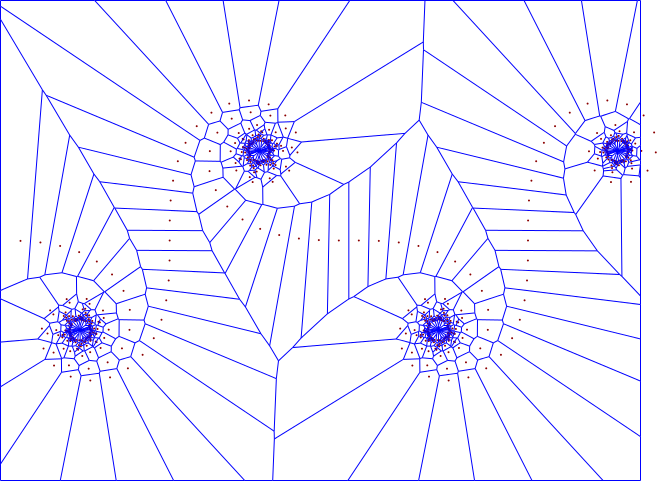
Avec la suite n³/1002

Le script montre le cadrage optimal :

f = (n) -> n*n*n/1002
nuage = []
P = [320,160]
for n in [1..1000]
    t=2*pi*f(n)
    P = [P[0]+10*cos(t),P[1]+10*sin(t)]
    nuage.push P
dessineVoronoi nuage, "blue", 0.5

Le diagramme est étonnamment symétrique :

Le logiciel de retouche d’image ImageJ possède un filtre « Voronoï ». Par exemple, en appliquant sur une image blanche le filtre « salt and pepper » qui engendre un nuage de points uniformément distribués (points noirs, d’un pixel chacun), le filtre Voronoï, on obtient quelque chose comme ceci :

Ce filtre sert à améliorer des images de cellules prises au microscope, pour les isoler et les compter.

Pour Blender, Voronoï est une texture. Par exemple, voici une « icosphère » bleutée, mais non texturée :

Pour lui donner un aspect moins uniforme, on modifie selon un diagramme de Voronoï, l’emplacement des points la composant. Pour texturer un objet, cliquer sur l’icône en forme de damier (en haut à gauche) puis, à l’aide du double triangle à droite, dérouler un menu dans lequel on peut choisir la texture « Voronoï » (par défaut c’est « nuage ») :

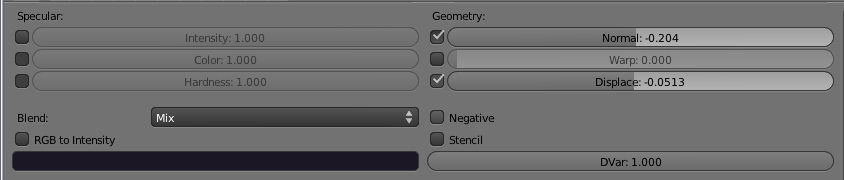
L’effet choisi a consisté ici à

• choisir une couleur magenta foncée (en bas) pour les creux
• appliquer la texture au rayon local de la sphère (« displacement », légèrement négatif)
• appliquer aussi la texture au vecteur normal (« normal », là aussi légèrement négatif) :

L’effet obtenu est un peu extraterrestre :

Ce n’est plus Voronoï, c’est plutôt verrue-noï !