Voici les points du programme de cycle 1 qui sont travaillés par cette activité :

Dans les onglets suivants, on aborde la construction du nombre et l’apprentissage de l’écriture.

L’activité a été menée en Grande Section, vers la fin du premier trimestre. La plupart des élèves disent ne pas savoir lire, mais tous savent écrire des lettres l’une après l’autre, comme avec l’activité sur les automates.

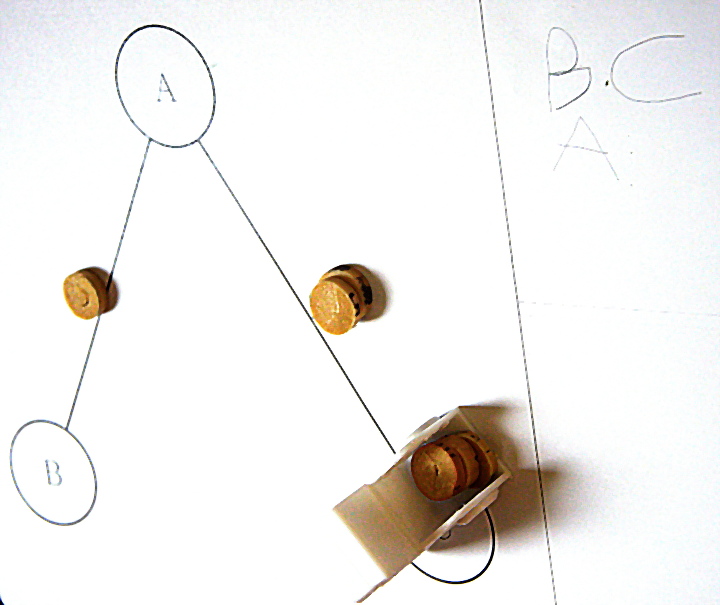
Mais écrire la deuxième lettre à droite de la première n’est pas encore naturel, l’écriture se fait parfois verticalement :

Ceci dit, la lettre suivante est quand même écrite à la droite du A :

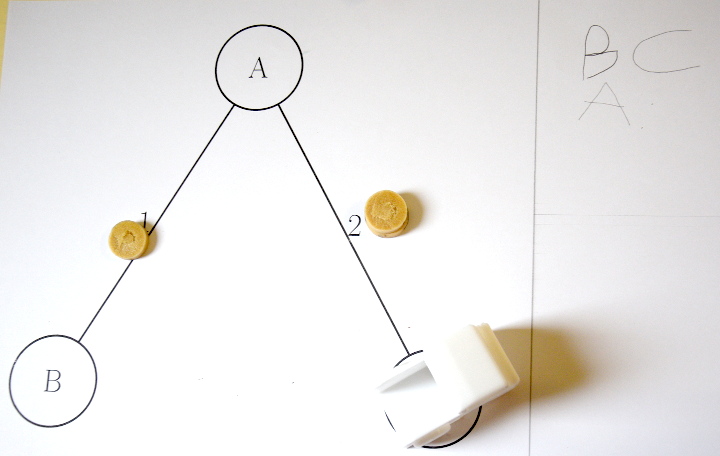
Et même lorsque le texte « BAC » est bien écrit de gauche à droite, on peut apercevoir un « C » à l’envers :

La camionneuse peut estimer le nombre de jetons dont elle aura besoin, soit avant d’avoir choisi le point de départ, soit après.

Sur des graphes simples, cela suppose que

• l’on sache quel chemin on va effectuer,
• l’on lise les chiffres donnant les montants aux péages,
• l’on estime le total de ces nombres,
• l’on compare ce total au nombre de jetons dont on dispose déjà,
• l’on sache alors combien de graines on doit demander en plus...

Comme dans le jeu de Fang, on voit alors une difficulté liée à la soustraction :

• Combien de jetons te faut-il ?
  • 6.
• Combien en as-tu déjà ?
  • 4.
• Combien dois-je alors t’en donner en plus ?
  • 6.

Dans le graphe ci-dessous il faut 3+2=5 jetons :

Or la camionneuse a demandé seulement 3 jetons pour faire le trajet :

Elle n’a donc pas encore perçu que « trois plus quelque chose » c’est plus que 3 [1].

Lorsque la camionneuse a réussi à finir le trajet avec un camion alors vide, elle a réalisé une optimisation, mais aussi une addition.

Par exemple on voit ici que 3+2 est égal à 5 (nombre initial de jetons dans le camion) :

Avec un tas de 3 jetons et un tas de 2 jetons, en GS, un bon moyen de savoir combien il y a de jetons en tout, est de les compter tous, mais pour cela il faut les regrouper. Plusieurs élèves ont du mal à faire ce regroupement préalable et comptent les tas (2) au lieu de compter les jetons (5).

Et ici, avec ce graphe :

est posée l’addition 3+5 :

En effet le camion est vide et donc le nombre initial de jetons est la somme des versements aux deux péages (3 et 5). Mais si à ce stade la camionneuse ne se souvient plus du nombre initial de jetons, elle devra compter les jetons, et pour cela :

• comprendre que ce sont les jetons qu’il faut compter et non les tas de jetons (la réponse 2 a été donnée plusieurs fois),
• penser à regrouper les 3 jetons et 5 jetons en un seul tas,
• compter les 8 jetons obtenus,

ou alors faire l’addition (on reconnaît une quinaire à laquelle 3 sont ajoutés, et on connaît la somme 5+3).

Ce graphe permet d’aborder la notion d’algorithme, puisqu’il faut en premier lieu estimer (avant de jouer) le besoin de la camionneuse en jetons (sa fiche de frais). Voici une trace de recherche constatée :

1. Le premier choix effectué a été celui de 6 jetons (probablement par imitation, les voisines ayant choisi aussi 6 jetons avant de commencer leur périple).
2. Constatant que 6 jetons ne suffisent pas (après avoir payé 3 jetons, il n’en reste plus que 3 au lieu des 5 attendus), il aurait été naturel de demander plus que 6. Mais le choix suivant a été 2 jetons.
3. Cela ne suffisant pas (même pour le premier péage), le choix suivant a été 3 jetons (l’élève n’a pas encore l’ordre des entiers : il faut bien plus que 2 jetons mais aussi plus que 6).
4. Après avoir demandé 4 jetons et constaté que cela ne suffisait toujours pas, une explication a été donnée à l’élève : il faut plus que 6 jetons.
5. Malgré cela, l’élève a demandé 5 jetons (en pensant peut-être que 5 est plus grand que 6).
6. Puis l’élève a demandé 10 jetons qui lui ont permis de faire le trajet jusqu’au bout. Mais avec un surplus à l’arrivé. À la question de savoir si on pouvait faire avec moins que 10 (mais plus que 6) la réponse n’est pas venue, faute de temps.

Plus loin on verra des additions à plus que deux nombres, sur des graphes plus complexes.

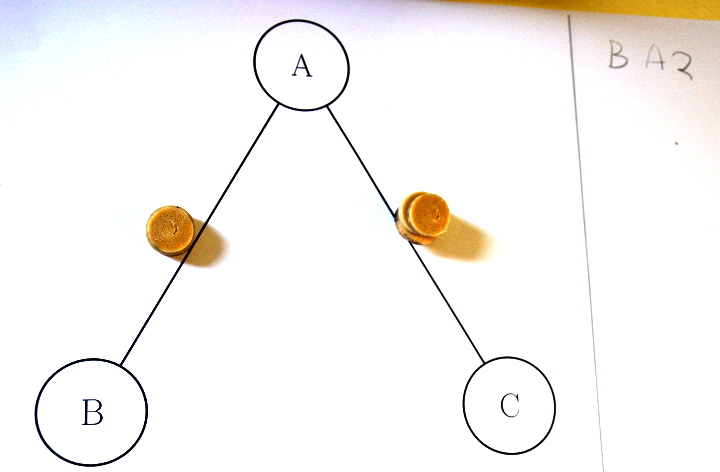
Jusqu’à présent on ne voyait que des chemins hamiltoniens : parcourir une fois seulement chaque sommet. Par exemple si on commence par A on est obligé de repasser par A et le chemin n’est plus hamiltonien. Il est alors nécessaire de commencer ailleurs qu’en A [2].

Mais avec ce graphe :

on est censé parcourir un circuit hamiltonien, c’est-à-dire revenir au point de départ. La confusion a parfois mené à des « erreurs » :

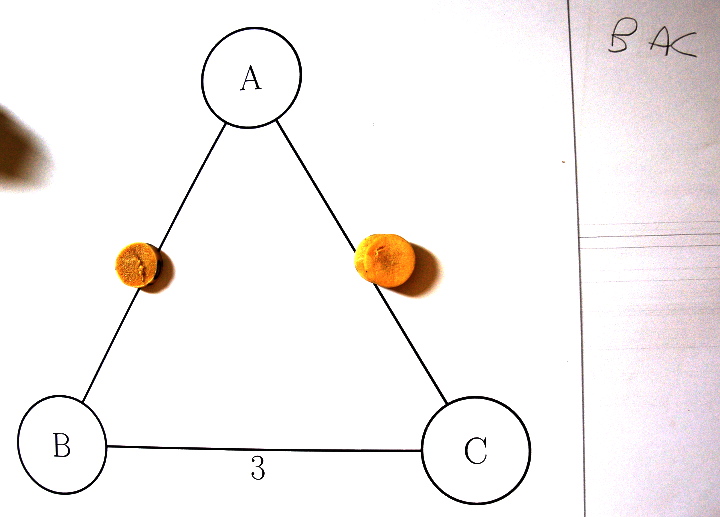
En fait comme le graphe est lui-même un circuit, peu importe où on commence, on aura besoin de 1+2+3=6 jetons si la camionneuse rentre chez elle à la fin de sa tournée :

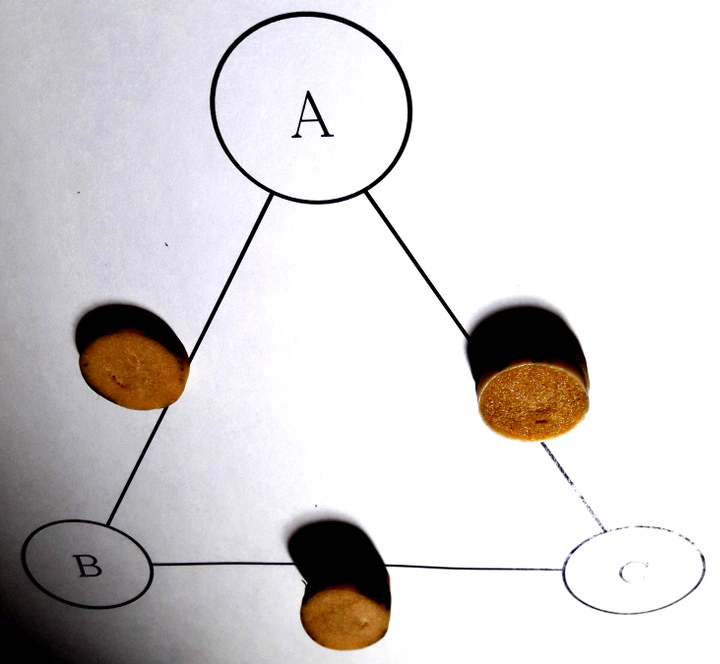
On remarque une tendance naturelle à adopter un algorithme glouton, consistant ici à payer d’abord le moins possible, c’est-à-dire

• partir de B
• aller vers A :

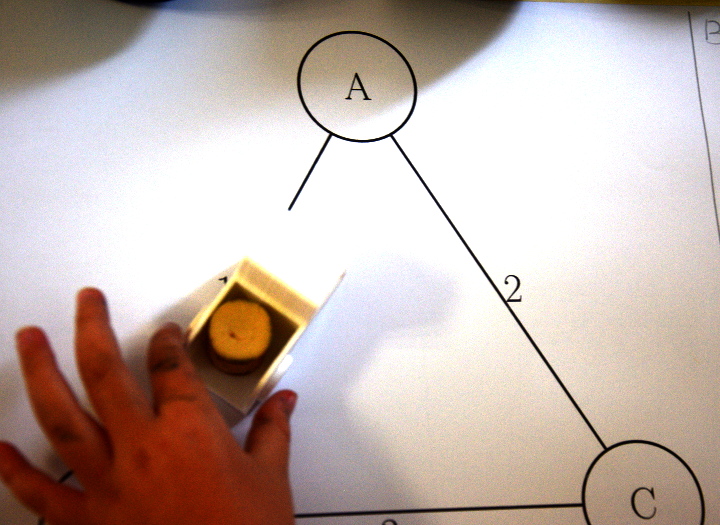
• payer un jeton au passage,
• de B, aller vers C (en laissant deux jetons au passage) :

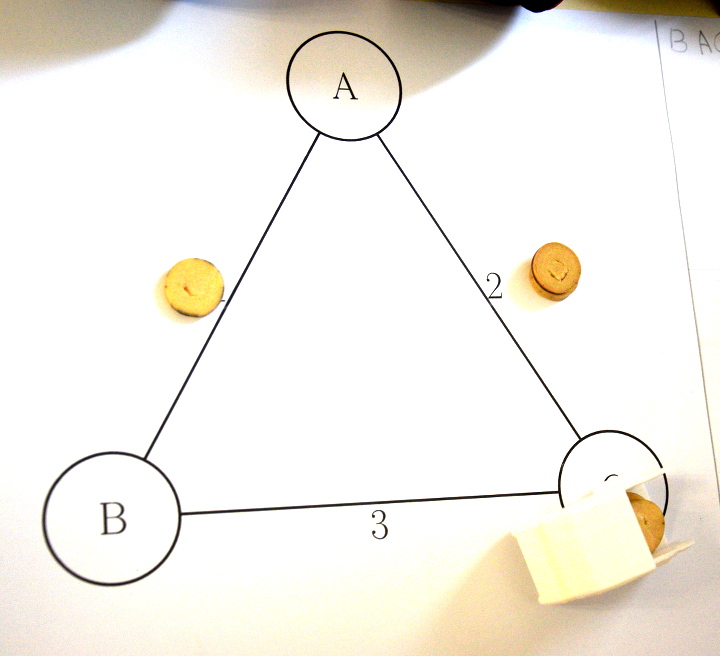
• puis finir en allant à nouveau vers A ce qui consomme les 3 derniers jetons.

Le fait qu’on aurait eu les mêmes besoins en commençant par une autre ville de départ, signifie que 1+2+3=2+3+1=3+1+2=3+2+1=2+1+3=1+3+2.

Place à ce graphe donné au concours Centrale-Supélec 2023 :

Le problème du voyageur de commerce n’a de sens que sur un graphe hamiltonien. Dans ce cas, il est d’usage qu’une fois toutes les villes parcourues, la camionneuse revienne à son point de départ. Après avoir joué sur des graphes plus simples, ce n’est pas spontané :

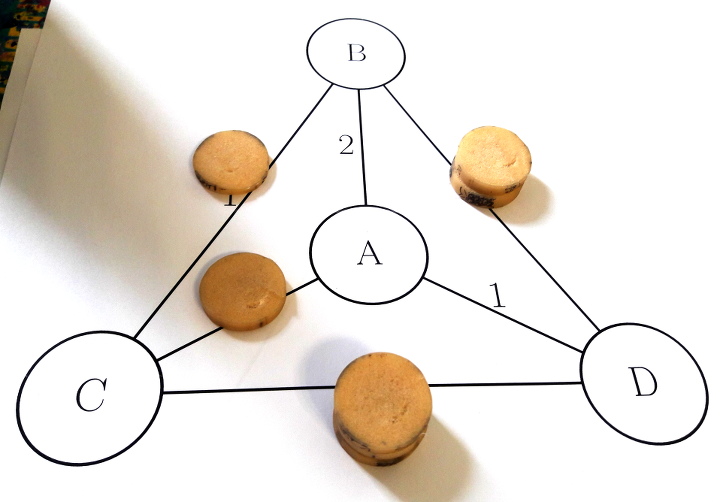
En fait, l’apprentissage d’un jeu complexe ne peut se faire qu’au sein d’une progression, et lorsqu’on franchit un palier, c’est par une modification de la règle du jeu (ici, il faut, en plus, revenir au sommet de départ) ce qui peut naturellement perturber des élèves de Grande Section.

Ici on voit une recherche en avant (BACBD à suivre de A probablement) écrit BCAD sur la feuille :

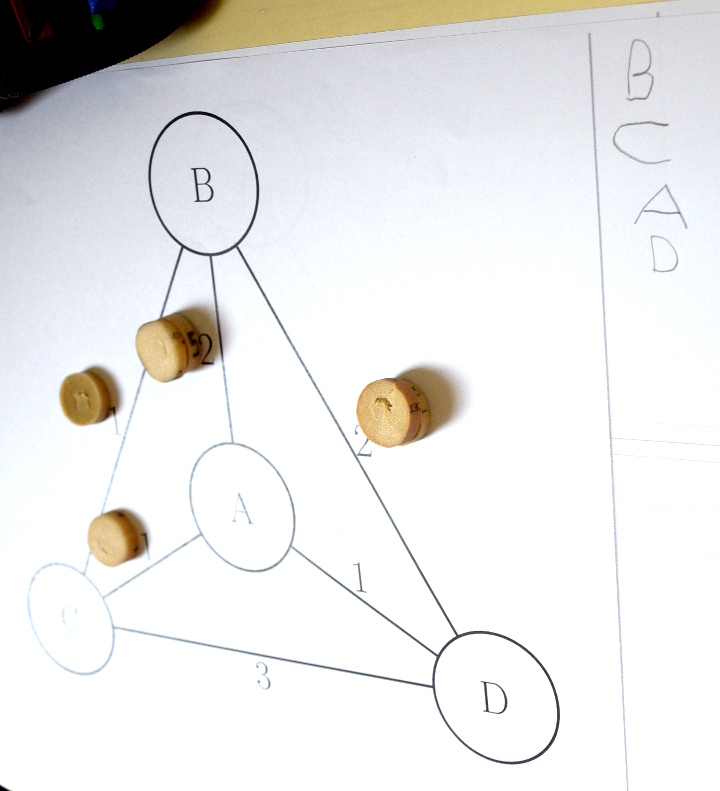
On remarque que BCADA était gagnant mais dans ce cas il aurait fallu laisser un jeton au péage DA et non deux jetons au péage AB qui n’a pas été emprunté.

Les plus motivées ont choisi aussi ce graphe qui attirait leur regard :

Avec ici une erreur sur l’arrivée (DEBCAE au lieu de DEBCAD qui a induit un payement inutile de 3 jetons sur le péage -inutile- de AE) :

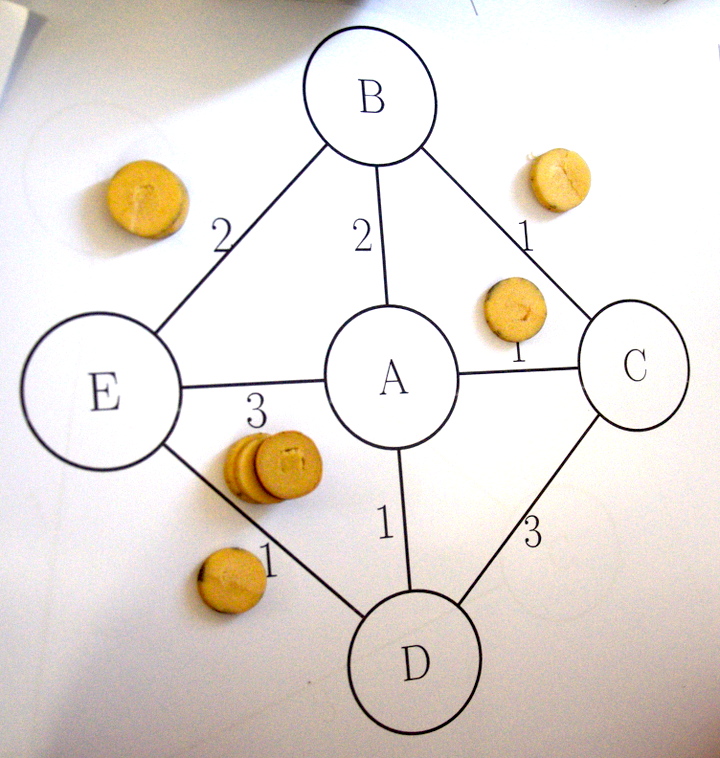
Le trajet a donc coûté 8 jetons sans même revenir au point de départ (D). Alors que DEBCAD n’en aurait coûté que 6 (1 de plus à payer encore, parmi les 2 dans le camion) :

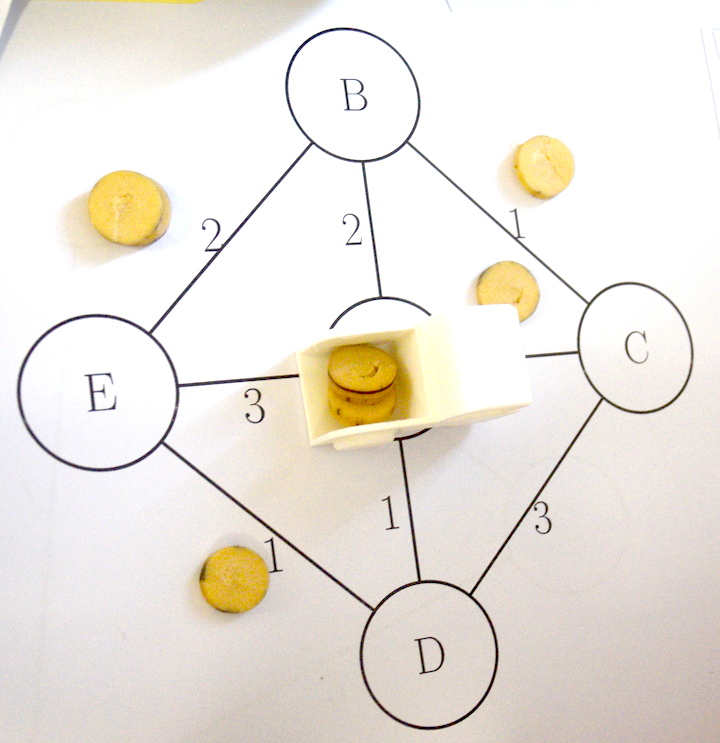
On voit là une perturbation de la tâche « trouver le trajet » par la tâche « payer le bon montant » : dans le premier cas, le fait qu’il reste encore 3 jetons dans la benne, incite la camionneuse à passer par ce trop tentant péage 3. Alors que dans le second cas, en n’ayant que 7 jetons au départ, la camionneuse voit qu’elle ne peut pas passer par cette impasse et a donc tendance à finir correctement, non parce qu’elle doit revenir au point de départ, mais parce qu’elle n’a plus d’autre choix.

L’activité mobilise

• la comparaison des nombres (nombre de jetons à comparer avec le montant au péage, nombre initial de jetons à comparer avec le total des sommes laissées aux différents péages, ...),
• le comptage (pour savoir combien de jetons il y a en tout),
• l’addition des nombres (pour estimer le coût total, on additionne les montants des différents péages traversés),
• la soustraction (pour savoir combien il restera de jetons après avoir effectué le tour).

En début de Grande Section, ces notions ne sont pas simples, surtout lorsqu’il y a des grands nombres (dépassant 10 au total). Par contre, trouver d’instinct un circuit hamiltonien est assez naturel pour la plupart des élèves. C’est la verbalisation de l’algorithme qui est plus difficile [3].

Avec les mêmes graphes, on peut aussi jouer à un autre jeu :

• On donne à la joueuse, le graphe, un camion et des jetons (sans oublier de lui demander combien il lui en faudra).
• On lui demande de poser le camion sur un sommet de son choix (ou alors on le choisit pour elle).
• On lui montre un autre sommet qui servira de destination.

Et maintenant, elle n’est plus chargée de parcourir toutes les villes, mais seulement d’aller à la destination désignée. En payant le moins possible.

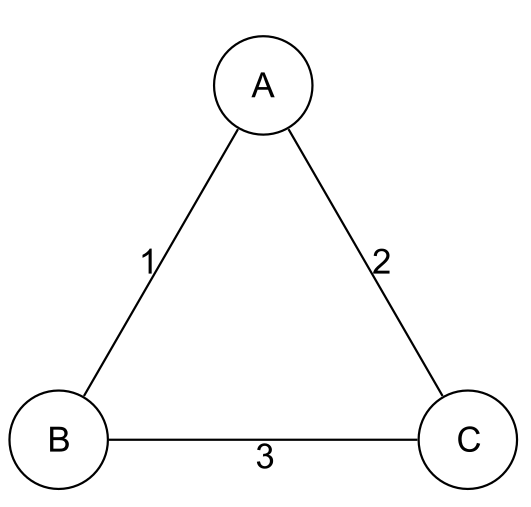
On reprend ce graphe (qui se trouve être hamiltonien mais ici ce n’est plus nécessaire) :

Pour aller de A à E il vaut mieux éviter de prendre le chemin direct qui coûte 3 jetons, alors qu’en effectuant un détour par D on paye 1+1=2 jetons seulement.

De même, le trajet de C à D par route directe coûte 3 jetons, alors qu’en effectuant un détour par A on paye 1+1=2 jetons.

Pour aller de C à E, on peut passer par A (mais alors on paye 4 jetons en tout), ou prendre l’un des chemins

• CBE de coût total 3 (1+2)
• CADE de coût total 3 aussi (1+1+1)

Ce graphe est issu du sujet zéro de NSI (2023) :

On demande de trouver le chemin le moins cher allant de G à E.

On commence par placer le camion en G, avec suffisamment de jetons (sinon on recommencera tout avec un plus grand nombre de jetons) :

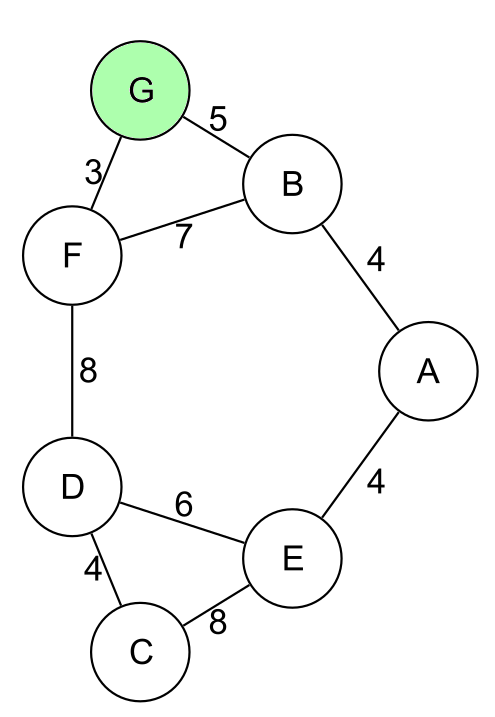
Pour démarrer le trajet, on a deux choix, F et B :

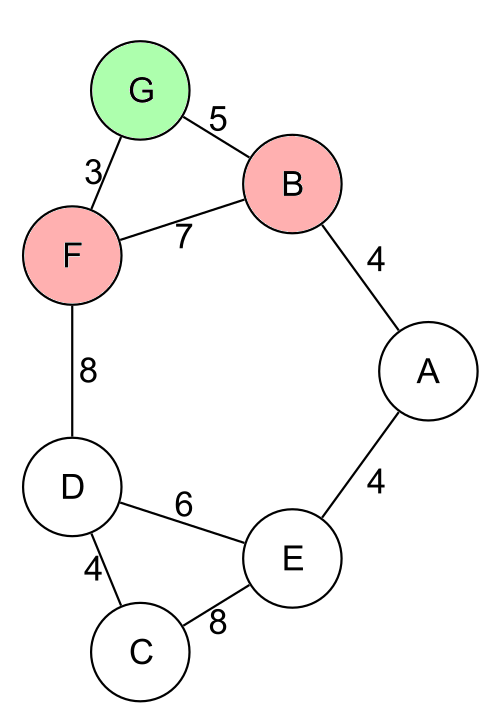
Le péage entre G et F étant moins cher que celui entre G et B, on a tendance à commencer par celui-ci. Mais

• si on commence par F, on va ensuite en D (B n’est pas avantageux),
• si on commence par B, on va ensuite en A :

Or le trajet GFD (dont on ne sait pas encore s’il va vite vers E) coûte 3+8=11 jetons et le trajet GBA ne coûte que 5+4=9 jetons. Donc a posteriori le choix de B devient plus probablement intéressant.

De fait, on constate que E est adjacent à la fois à D et A, avec un coût total

• 3+8+4 = 15 jetons pour GFDE
• 5+4+4 = 13 jetons pour GBAE

Le meilleur trajet est donc finalement GBAE avec un coût total de 13 jetons :

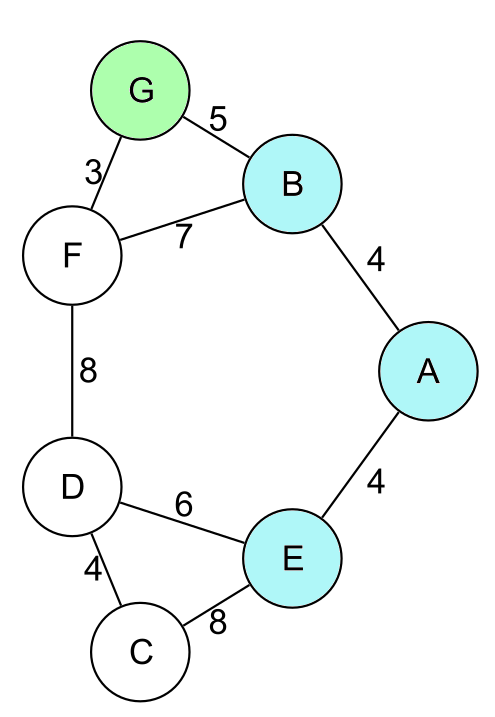
Un élève de GS ayant testé l’activité a bien trouvé ce trajet mais a eu du mal à estimer le nombre de jetons nécessaires (une vingtaine).

Le coloriage par couches de couleurs (vert, rouge,cyan) est appelé parcours en largeur d’abord et est à la base de l’algorithme de Dijkstra datant de la fin des années 1950.

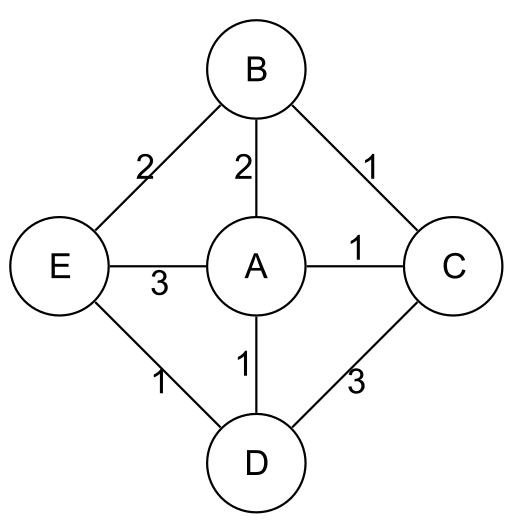
Le jeu suivant a été proposé par Alcuin d’York à Charlemagne comme exercice de maths :

Le camion, d’une capacité de 3 jetons maximum, est placé en B où se trouvent 6 jetons. La camionneuse doit en livrer le plus possible en C, mais en laisser un à chaque passage à un péage.

Une solution simple est de prendre 3 jetons (le maximum possible) puis aller en A (il ne reste alors plus que 2 jetons) et en C. Il ne reste alors plus qu’un jeton à déposer en C. Et il n’y a plus de jeton, le camion est alors bloqué en C.

Une meilleure solution est de

• prendre 3 jetons (le maximum),
• aller en A (il ne reste alors que 2 jetons),
• déposer un jeton en A (il n’en reste alors qu’un),
• revenir en B (le camion est alors vide),
• prendre les 3 jetons restants,
• revenir en A (il ne reste alors que 2 jetons),
• prendre le jeton qui était en A (ce qui fait un total de 3 jetons),
• aller en C (il ne reste alors que 2 jetons),
• déposer en C les 2 jetons restants.

Soit le double de la solution simple précédente !

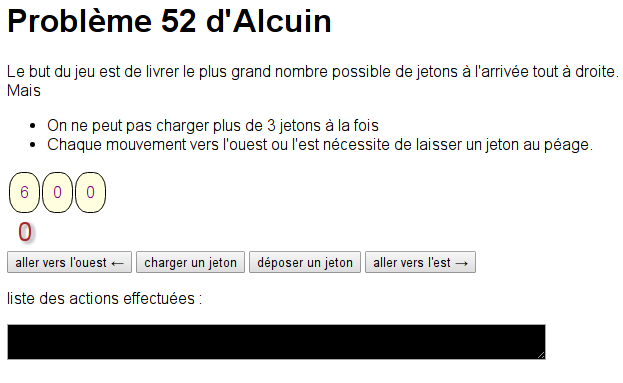
Sur le même graphe à 2 péages, on peut aussi essayer le jeu suivant :

Le camion, d’une capacité de 5 jetons maximum, est placé en B où se trouvent 10 jetons. La camionneuse doit en livrer le plus possible en C, mais en laisser un à chaque passage à un péage.

Dans ce cas de figure, on peut livrer jusqu’à 4 jetons en C.

Pour tester les jeux de l’onglet précédent, on peut utiliser l’une des pages web suivantes (les arêtes ne sont pas dessinées, ni les montants des péages qui valent tous 1) :

• Avec 6 jetons au départ, capacité du camion 3 :

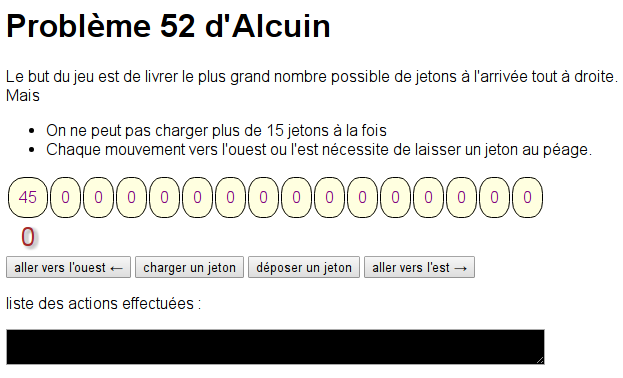
• Avec 10 jetons au départ, capacité du camion 5 jetons :

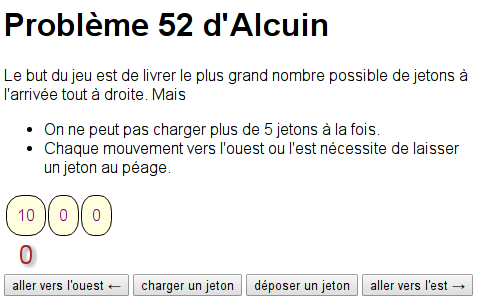
Les situations vues dans les onglets précédents peuvent servir à démarrer une progression vers le jeu classique d’Alcuin. Ici on présente des situations similaires (pas au niveau de GS, et pas jouables avec le matériel actuel puisque la capacité du camion est 15 jetons).

Le jeu suivant est similaire aux précédents, à ceci près qu’il faut trouver où effectuer le stock intermédiaire (essayer de placer un maximum de jetons 10 sommets plus loin que le départ) :

Et celui-ci est un peu plus complexe, avec 12 péages entre le départ et l’arrivée :

Et celui-là est encore plus complexe, avec le besoin de faire non pas une escale pour un stock intermédiaire, mais deux (reste à savoir où !) :

Enfin l’étape finale de cette progression est le problème originel d’Alcuin, avec un chemin de longueur 30 et 90 jetons au départ, la capacité du camion (un chameau chez Alcuin) étant de 30 :

Dans le jeu originel d’Alcuin, il s’agissait de livrer le plus grand nombre possible de jetons à une distance donnée du départ. On peut en faire un jeu à plusieurs joueuses, la (les) gagnante(s) étant celle(s) qui en livre(nt) le plus.

Une variante est apparue au milieu du XX^e siècle où le camion ne va plus déposer les jetons à un endroit prédéterminé, mais continuer sa route le plus loin possible. Dans les deux cas il faut (à cause du péage dans le second cas) un maximum de jetons.

Cette variante permet de faire une sorte de course, où la ganante est celle qui a réussi à aller le plus loin possible. En voici une version avec affichage des arêtes (sans mention du péage égal à 1), où il s’agit d’aller le plus loin possible avec un camion (ou une jeep, véhicule réputé gourmand en carburant) avec 6 jetons au départ, la capacité du véhicule étant de 3 jetons maximum (ce qui permet de dessiner les constellations) :

Les 45 jetons à livrer dans l’onglet précédent deviennent une course où il faut essayer de dépasser la distance 20 :

Et le problème initial d’Alcuin devient une course où on essaye d’aller au-delà de la distance 40 :