Nous sommes enseignantes, l’une en mathématiques, l’autre en lettres modernes, au collège Henri-Matisse de Saint-Pierre, un collège doté des moyens RAR cette année, et devenant ECLAIR à la rentrée 2011.
Notre sixième est une sixième standard dans notre établissement : hétérogène, mais avec beaucoup d’enfants en difficultés tant sur le plan des apprentissages (près de la moitié de nos élèves ont obtenu des résultats inférieurs à 33% de réussite aux évaluations nationales de CM2) que sur celui du comportement en classe.
Dans le cadre du socle commun de connaissances et de compétences, et précisément dans l’optique d’aider chaque élève à mieux progresser, nous avons réuni une équipe pédagogique autour d’un travail commun : des pratiques de classe et des évaluations centrées sur l’acquisition des mêmes connaissances, capacités et attitudes, dans toutes les disciplines :
| apprendre | s’informer | raisonner | réaliser | communiquer | s’investir | vivre ensemble |
Cela se traduit, sur le bulletin trimestriel, par une grille transversale commune, déclinée en points verts, orange et rouges, où la note est secondaire. Nous mettons donc l’accent sur l’évaluation des attitudes attendues dans toutes les disciplines et indispensables à l’exercice du métier d’élève.
Pour donner plus de sens aux apprentissages et motiver les élèves, nous avons également choisi de faire le lien entre les mathématiques, le français et la culture de nos élèves, en leur proposant d’écrire des « contes mathématiques réunionnais ». Pour mener à bien ce projet, nous avons animé tout au long de l’année une heure hebdomadaire de maths–français. Nous avons aussi emmené les enfants au CALÉ (Centre Académique de Lecture et d’Écriture) de l’Entre-Deux pendant une semaine, à la fin du mois de novembre.
Voici donc le déroulé de cette expérience, telle que nous l’avons menée au fil de l’année.
I - L’AVANT CALÉ : L’HEURE DE « FRANÇAIS-MATHS »
Nos ambitions étaient de travailler, d’une part sur l’univers du conte merveilleux, d’autre part sur la résolution de problèmes mathématiques. Nous attendions des élèves des narrations de recherche sur des problèmes existants puis l’élaboration, par les élèves, de problèmes mathématiques susceptibles de devenir des supports de contes.
1. Tâtonnements et difficultés
Dès le début de l’année, nous avons lancé nos élèves sur la narration de recherche d’un problème de type rallye. Le problème nous paraissait simple. C’était, du moins nous le pensions, surtout de la prise d’information.
Les difficultés ont été multiples :
- D’une part les élèves n’ont pas compris l’énoncé, ils n’ont donc pas pu prélever les informations utiles. Et ils n’ont pas trouvé de stratégie de résolution du problème.
- D’autre part, avec deux enseignantes de matières différentes, les élèves ne savaient pas trop ce que nous attendions d’eux (Pouvaient-ils poser des questions sur le problème de maths à la prof de français ? Et la prof de maths, pourquoi voulait-elle une rédaction ? ...etc.).
À la fin de l’heure, le problème n’était pas fini : la tâche était trop longue, trop complexe et de ce fait démotivante.
Mais nous aussi, nous avons été en difficulté : nous découvrions la co-animation en même temps que l’équation suivante : deux fois plus de profs = deux fois moins d’efficacité !
Les heures passaient sans que les narrations de recherche n’avancent : les élèves ne comprenaient pas ce que nous attendions d’eux, et nous ne réussissions pas à le leur expliquer clairement.
2. Recherche de solutions et premières réussites
Nous avons alors mis de côté les problèmes que nous pensions traiter en narration de recherche et avons choisi d’aborder des tâches moins complexes, relevant de la lecture d’énoncés. L’objectif de l’exercice n’était pas de trouver la réponse, ni de faire le calcul. Nous voulions que les élèves réfléchissent au sens de l’énoncé et des données : quelles sont les informations qui permettent de répondre à la question, de quoi ai-je besoin pour répondre ? Il s’agissait de mettre l’accent sur l’importance de la démarche et de la réflexion avant de faire des calculs. Nous voulions faire passer l’idée que résoudre un problème mathématique, c’est avant tout mener une démarche de réflexion, un travail de logique, et par conséquent des essais, des tâtonnements, les calculs n’étant qu’une étape, et pas la première.
Par la suite, nous avons toujours mis en valeur la démarche engagée plus que l’aboutissement du problème.
Finalement, nous avons trouvé une activité que les élèves ont pu accomplir en une heure ! Ils ont travaillé en collaboration. De notre côté nous avons réussi à co-animer la classe en prenant chacune en charge certains groupes (et non pas en tournant de groupe en groupe), nous nous sommes clairement partagé les rôles.
La tâche complexe était suffisamment simple pour être accomplie en une séance, ce qui a motivé les élèves qui ont eu le sentiment d’avancer et de réussir. Il s’agissait d’un problème de logique mobilisant des connaissances en mathématiques (additionner des grands nombres) et en français (un énoncé simple à reconstituer sous forme de puzzle puis à traiter).
Le français était un véritable outil pour résoudre le problème mathématique. En effet il leur fallait faire le lien entre leurs connaissances des règles de ponctuation et de grammaire et les mots écrits sur chaque pièce du puzzle pour reconstituer les phrases. Une autre connaissance mise en œuvre était l’écriture des nombres en lettres. En effet, le sens de l’écriture des nombres (la numération) donnait aussi des éléments de réflexion pour la reconstitution des phrases. Ainsi les étiquettes “cinq mille” et “cent mille” ne pouvaient pas s’accrocher.
Du point de vue mathématique, les élèves étaient en résolution de problème puisqu’ils ont pris les informations sur chaque étiquette, ils ont fait le lien entre leurs connaissances en grammaire et en numération pour reconstituer le puzzle, ils ont ensuite eu à répondre à la question posée. Quant au problème mathématique en lui-même, les élèves ont choisi la bonne opération (ici aucune difficulté, il s’agissait d’une addition) puis ont mis en œuvre l’addition des grands nombres. Ils ont alors répondu à la question avec les bonnes unités (le nombre d’habitants), l’objectif était plus de penser à préciser l’unité qu’à la choisir.
3. Nos trois dernières séances avant le CALÉ
Les vacances d’octobre approchaient et nous avons dû revoir nos objectifs : nous voulions toujours que les problèmes mathématiques soient le ressort des intrigues, mais nous n’avions plus le temps de laisser les élèves créer les problèmes. Nous avons alors choisi de traiter trois énigmes mathématiques, puisque les élèves seraient en trois groupes. À eux ensuite de choisir le problème et de fabriquer la trame. Histoire de les “mettre dans le bain”, nous avons habillé les problèmes en les plaçant dans un contexte de contes traditionnels :
II - LE CALÉ : L’ÉCRITURE DES « CONTES MATHÉMATIQUES RÉUNIONNAIS »
1. Le déroulement de la semaine
Au CALÉ les élèves étaient répartis en trois groupes hétérogènes. Chaque groupe a pu rendre visite à un artisan différent : un bardottier, un artisan du café et un du choka (le choka est une plante dont les feuilles sont utilisées dans l’artisanat).

Les visites ont été l’occasion d’enrichir le vocabulaire des enfants, d’élargir leurs horizons et de découvrir des savoir-faire. Le but pédagogique était de découvrir le patrimoine local pour y situer les contes et ainsi fournir un cadre à l’énigme mathématique.
Tout au long de la semaine, les élèves ont élaboré les contes très progressivement, ne passant à l’écriture qu’au dernier moment. Ainsi, après avoir réuni les éléments constitutifs du conte (les personnages, les lieux, le vocabulaire du patrimoine local pouvant être utilisé), les élèves ont élaboré la trame narrative à l’oral, en groupe. Les premières difficultés pour les élèves ont été la verbalisation des idées. Beaucoup avaient du mal à les exprimer clairement, à respecter l’ordre chronologique, à visualiser les déplacements du héros. Tout ce travail à l’oral nous a semblé très long, mais il a permis aux élèves de s’approprier l’histoire et le problème. Cette activité, relevant plus traditionnellement du cours de français, a été une vraie valeur ajoutée à la compréhension du problème mathématique. En effet, réfléchir à la trame a obligé les élèves à maîtriser les données du problème (de quoi dispose le héros, quelles sont ses difficultés, dans quel ordre interviennent les indices ?).
Cette construction de la trame narrative a nécessité une prise de recul par rapport au problème qui n’a été possible qu’une fois le problème parfaitement compris. Là encore le français a permis d’enrichir la réflexion des élèves.
2. Le nœud du problème
La principale difficulté que les élèves ont rencontrée était de faire le parallèle entre la définition du conte mathématique - définition que nous avons élaborée ensemble - , et celle du conte merveilleux. En effet nous voulions créer une structure qui réponde à la fois à une logique narrative et à une logique mathématique.
Le héros est confronté à un problème mathématique qu’il doit résoudre (pour réussir à accomplir une mission) ;
il doit donc réfléchir, élaborer des hypothèses,
demander de l’aide auprès de personnages qui vont lui donner des indices ;
à la fin, il réussit à résoudre son problème, et cela va changer sa vie.
Partant de cet objectif, les élèves ont donc construit une trame : ici, celle de Zaphir et les cerises de café.

3. Trois problèmes, trois contes
Avant de passer à l’écriture même du conte, les élèves ont reformulé le problème mathématique afin de bien se l’approprier. Les problèmes avaient été cherchés et corrigés en classe avant le CALÉ, mais cette étape a été nécessaire pour chaque groupe. Une réflexion collective s’est ensuite engagée pour faire le lien entre l’activité artisanale visitée plus tôt dans la semaine et le problème mathématique choisi. Notre objectif était de placer le problème mathématique au cœur de l’intrigue, à savoir que la progression du héros devait être celle de la résolution du problème.
L’univers est bien celui du conte merveilleux, car il y a de la magie et des personnages qui font partie de la culture réunionnaise (Grand-mère Kalle), et la trame narrative suit la démarche de résolution de problème. Le héros découvre son problème et l’explicite dès le début du conte. Les personnages rencontrés servent à donner des indices, que les élèves ont imaginés à partir de leurs propres conjectures (celles qu’ils avaient émises lors de leur résolution de l’énigme mathématique). Voici la trame à laquelle ils ont abouti :
A. Zaphir et les cerises de café : Zaphir est un esclave qui, pour sortir de sa condition, se voit offrir 10 cerises de café, qui ne pousseront que s’il les plante de façon à obtenir 5 lignes de 4 cerises.
B. Le problème de Monsieur Tétia : M. Tétia est un bardottier qui doit transporter sur sa petite barque son civet de canard, son petit-fils et grand-mère Kalle (sorcière locale qui effraie les enfants), sachant d’une part que sa barque ne peut accueillir qu’une personne et une chose, à la limite deux personnes, d’autre part que le petit-fils risque de dévorer le civet, et grand-mère Kalle le petit-fils !!! Hors de question d’associer ces deux couples dans la barque...
C. Jacqueline et les deux pots : Jacqueline est une artisane qui fabrique des savates en choka, et découvre une recette permettant de fabriquer des savates magiques... à condition de résoudre un problème d’eau.
III - L’APRÈS CALÉ
1. Bilan du CALÉ
À la fin de la semaine, les élèves sont repartis avec le conte écrit collectivement par le groupe. Beaucoup d’entre eux ont été valorisés et les plus timides ont pris confiance en eux. Ils ont essayé de l’oraliser à la fin de la semaine.
Le conte qui nous a paru le plus abouti, non d’un point de vue littéraire, mais pour ce qui concerne la « mise en histoire » du problème mathématique, est celui de « Jacqueline et les deux pots ». En effet, au début du conte, l’héroïne, Jacqueline, artisane du choka, se fixe elle-même une mission : celle de fabriquer des savates en choka pour ses petits-enfants (pour Noël) ; or, l’apparition du problème mathématique va être l’élément qui fait entrer le merveilleux dans l’histoire, et en crée donc tout l’intérêt. Si Jacqueline réussit à résoudre le problème mathématique, elle ne va pas se contenter d’offrir des savates en choka à ses petits-enfants, mais elle va leur donner des savates magiques, c’est-à-dire des savates qui rendent heureux !
Elle trouve donc une recette pour fabriquer les dites savates. Pour que la magie fonctionne, il faut avoir exactement 4 litres d’eau. Or, Jacqueline n’a que deux pots, un de 3 litres et un de 5 litres.
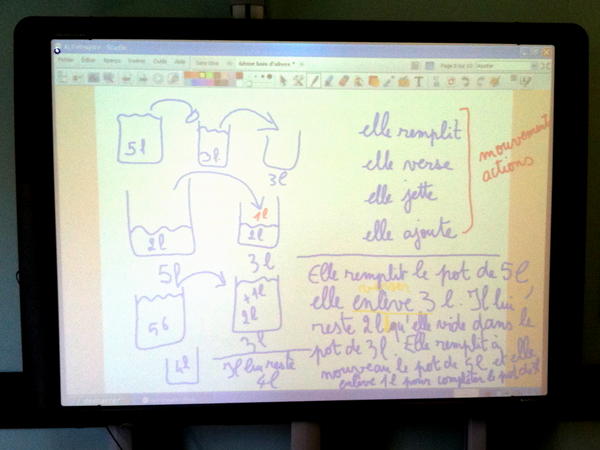
D’autre part, au fil de l’histoire, Jacqueline se fait scientifique, du moins elle adopte une démarche de résolution de problème : elle réfléchit, fait des calculs, pose des hypothèses, expérimente des essais de remplissage avec ses pots... et en plus elle raisonne ! Quand le facteur vient la voir et se mêle innocemment de remplir et vider ses pots, Jacqueline l’observe, analyse ce qu’il fait, interprète et conclut... et comprend qu’à l’aide du facteur, elle a résolu son problème d’eau : elle a réussi à obtenir exactement 4 litres d’eau avec ses deux pots. Il ne lui reste plus qu’à fabriquer les savates magiques, et ça marche, ses petits enfants les ayant chaussées deviennent tout heureux !
Dans ce conte la résolution du problème mathématique « coule de source », c’est elle qui fait progresser la narration et mène l’intrigue vers sa propre résolution. Logique mathématique et logique narrative vont de pair.

Tout est lié : le problème mathématique donne une valeur ajoutée à l’activité artisanale, il est le ressort de l’intrigue, il introduit le merveilleux dans le conte et il transforme les personnages :
- Il permet le bonheur des petits-enfants de Jacqueline.
- Jacqueline devient une scientifique, et qui plus est ravie de l’être...
Moralité du conte : qui sème des maths récolte du bonheur !
Plus sérieusement, les élèves se sont approprié les problèmes (et la démarche de résolution), ils les ont parfaitement intégrés, « digérés », et les ont... aimés !
2. L’oralisation
Nous avons envisagé de faire reprendre les deux autres contes aux élèves afin de les enrichir en renforçant les liens entre la progression de l’histoire et la résolution du problème. Mais ces deux contes avaient déjà leur propre logique narrative, et la tâche nous a semblé trop ardue. Nous avons donc laissé les contes écrits tels quels, et avons préféré poursuivre notre travail par l’oralisation et la mise en scène.
Nous avons donc fait appel à une association, FAIR (et notamment à Fatima Hanini), pour nous aider à mettre en scène et en film les trois contes. Nous voulions aboutir à une production qui ne soit pas uniquement écrite, pour développer d’autres compétences chez nos élèves : la mémorisation des textes, l’oralisation face à la caméra, le jeu silencieux (permettant d’exprimer des émotions sans la parole)...
IV - CONCLUSION
Cette aventure a été positive à plusieurs égards :
- Le projet a permis une cohésion du groupe classe et une prise en compte de chaque élève, même les plus en difficultés, à chaque étape de son élaboration.
- Le projet a aussi permis de donner du sens aux attitudes attendues et évaluées en classe tout au long de l’année (dans toutes les disciplines).
Nous disposions de peu de temps et d’argent, et les trois films (visibles sur le site, avec les textes des contes) sont de facture très artisanale ; mais ce travail a permis à des élèves de mettre en oeuvre des compétences qu’ils n’auraient sans doute jamais développées autrement cette année ; d’ailleurs, tous nous ont dit à quel point ils avaient apprécié ce projet, et particulièrement sa phase finale, celle de la création des trois films.
Le travail de cette année s’inscrit complètement dans l’esprit du socle commun de compétences et de connaissances, car les élèves ont eu à résoudre de multiples tâches complexes, et ont travaillé en inter et en trans-disciplinarité. En effet :
| On fait du français parce que | compétences | On fait des maths parce que |
|---|---|---|
| - on apprend la conjugaison au passé simple et imparfait ; on acquiert du vocabulaire et une culture | Apprendre | - on apprend une méthodologie pour résoudre des problèmes |
| on s’informe sur
- les contes merveilleux - le patrimoine |
s’Informer | - on prend l’information utile dans l’énoncé |
| - on analyse les contes lus
- on fait la synthèse des points communs entre les contes lus - on élabore la trame narrative des contes écrits |
Raisonner | - on fait des essais, on émet des hypothèses
- on valide ou non ses hypothèses, on développe son esprit critique |
| - on conçoit et on réalise des contes (tâche complexe menée à bien : construction d’un récit intéressant, pertinent, cohérent) ; on les oralise et on les met en scène | Réaliser | - on met en pratique une démarche en s’aidant de schémas, en faisant des calculs |
| - on met le conte en phrases : correction de l’expression écrite, puis de l’expression orale | Communiquer | - on raconte comment on a trouvé et ce qu’on a trouvé |
| - on s’implique personnellement dans le projet | s’Investir | - on s’implique personnellement dans le projet |
| - on respecte et on prend en compte les autres (groupes et classe). | Vivre ensemble | - on respecte et on prend en compte des autres (groupes et classe). |
Enfin, nous avons pu constater à maintes reprises à quel point travailler le français pouvait faire progresser en maths - et vice-versa ; mais aussi, à quel point les convergences entre ces deux matières a priori éloignées étaient nombreuses, pour ce qui concerne la mise en oeuvre et la mise en forme d’une réflexion logique et rigoureuse.
Nos remerciements les plus chaleureux vont à Séverine Henry et à toute son équipe du CALÉ de l’Entre-Deux, ainsi qu’à l’association FAIR (notamment Fatima et Sylvain), sans qui tout ce projet n’aurait pu aboutir.

Commentaires