La logique épistémique traite non seulement de la valeur de vérité de propositions telles que 2+2=4 ou la carte de Daniel est rouge, mais aussi de l’accessibilité que plusieurs personnes ont à ces valeurs de vérité. Ces personnes sont nommées agents [1], et de même qu’on note ¬, ∧ et ∨ la négation, la conjonction et la disjonction en logique épistémique comme en logique propositionnelle, on note K_D(p) la proposition épistémique « p est vraie et Daniel le sait », avec les notations analogues K_M(p), K_F(p) et K_A(p) pour dire respectivement que Marc, Franck ou Alain sait que p est vraie.

Les quatre agents étant supposés logiciens, toute proposition p vraie dans la logique classique vérifie automatiquement K_D(p) et idem pour les autres agents ; mais aussi K_D(K_F(p)) par exemple. Ainsi,

• 2+2=4 (théorème de la logique classique)
• K_D(2+2=4) (Daniel, parfait logicien, sait que 2+2 font 4)
• K_M(2+2=4) (Marc aussi, se débrouille en logique)
• K_F(K_M(2+2=4)) (Franck sait que Marc est logicien, et sait donc que Marc est au courant pour 2+2)
• etc

Comme il n’y a pas de limite au nombre d’opérateurs du type K_A devant une proposition de la logique classique, on réunit toutes ces propositions où 2+2=4 est précédé d’un nombre quelconque de ces opérateurs, sous une nouvelle proposition notée NP(p) et se lisant « p est de notoriété publique ». Ainsi,

• 2+2=4 (si, si !)
• chacun des 4 agents est suffisamment bon logicien pour savoir que 2+2=4 ;
• les 4 agents se connaissent suffisamment bien pour savoir que les autres agents sont au courant pour 2+2 ;
• etc

Ce qu’on note simplement NP(2+2=4) : Le fait que 2+2=4 est notoire parmi les 4 agents.

Dans cet exercice de Rallye, la couleur de la carte de Daniel n’est justement pas de notoriété publique : Au début, Daniel ne connaît pas cette couleur, et Marc sait que Daniel ignore cette couleur (alors que lui-même la connaît).

Par contre, une proposition peut être vraie sans que Alain le sache (évidemment, ceci n’est pas vrai pour une proposition de la logique classique). Par exemple, on sait (enfin Alain sait) que

• F♥ ∨ F♠

(la carte de Franck est rouge ou elle est noire), et donc

• K_F(F♥ ∨ F♠)

(Franck sait que sa carte est dans une de ces deux couleurs), mais aucune des propositions suivantes n’est vraie :

• K_F(F♥)
• K_F(F♠)
• K_A(F♥)
• K_A(F♠)

(Franck, comme Alain, ignorent laquelle des deux couleurs est dans la main de Franck)

Comme on ne s’intéresse pas à la couleur des deux cartes non distribuées, on est face à 8 mondes où sont données les couleurs des cartes des trois agents :

• F♥→M♥→D♥ (monde impossible puisqu’il n’y a que deux cartes rouges dans le jeu) ;
• F♥→M♥→D♠
• F♥→M♠→D♥
• F♥→M♠→D♠
• F♠→M♥→D♥
• F♠→M♥→D♠
• F♠→M♠→D♥
• F♠→M♠→D♠

Une proposition épistémique est considérée comme vraie si elle l’est dans tous les mondes possibles (les 7 derniers ci-dessus). Mais si une proposition est de la forme K_Ap, pour qu’elle soit vraie, il faut que p soit vraie dans tous les mondes accessibles à l’agent A. Les flèches ci-dessus figurent la relation d’accessibilité entre les mondes de Franck, de Marc et de Daniel telle que donnée dans l’énoncé. La relation d’accessibilité est supposée transitive : Tout ce que sait Marc est connu de Franck, et donc il faudrait rajouter une flèche allant directement de Franck à Daniel ; celle-ci est supposée sans être dessinée. Pour le deuxième des mondes ci-dessus (le premier des mondes possibles), le diagramme complet ressemblerait plutôt à ceci :

Dans ce monde, les propositions suivantes sont vraies :

• F♥
• M♥
• D♠
• K_M(D♠) (d’après la flèche, comme Marc voit la carte de Daniel, Marc sait que celle-ci est noire)
• K_F(M♥)
• K_F(D♠) (la relation d’accessibilité étant, dans ce problème, transitive).
• mais ¬K_F(F♥) (Franck ignore la couleur de sa carte)

Comme M♥ ∧ D♥ ⇒ F♠ (parce qu’il n’y a que deux cartes rouges dans le jeu), et que Franck est logicien, on a

• K_F(M♥ ∧ D♥ ⇒ F♠)

Or le fait que Franck est logicien, s’exprime en partie par l’axiome suivant de la logique épistémique : K_F(p⇒q) ⇒ (K_Fp ⇒ K_Fq) ; dans le cas présent, cet axiome permet de déduire que

• K_F(M♥ ∧ D♥) ⇒ K_F(F♠)

Dans le monde suivant :

• F♠→M♥→D♥

la proposition suivante devient alors vraie (alors qu’elle ne l’est pas dans les autres mondes) :

• K_F(F♠)

Or, l’affirmation de Franck s’exprime ainsi en logique épistémique :

• ¬ K_F(F♥) ∧ ¬ K_F(F♠)

(Franck ne sait pas que sa carte est rouge, et il ne sait pas que sa carte est noire) ; cette affirmation est contradictoire avec K_F(F♠) d’après cet axiome de la logique propositionnelle :

• ¬ K_F(F♥) ∧ ¬ K_F(F♠) ⇒ ¬ K_F(F♠) ;

On a montré par l’absurde que le modèle F♠→M♥→D♥ est à éliminer.

Donc (d’après l’onglet précédent), il ne reste plus que 6 des mondes initiaux (l’un est impossible, un autre exclu par l’affirmation de Franck) :

1. F♥→M♥→D♠
2. F♥→M♠→D♥
3. F♥→M♠→D♠
4. F♠→M♥→D♠
5. F♠→M♠→D♥
6. F♠→M♠→D♠

Par ailleurs, toujours d’après l’onglet précédent, la proposition ¬ (M♥ ∧ D♥), affirmée indirectement par Franck, devient de notoriété publique entre les trois agents (et même les 4, Alain, étant à l’écoute des trois, ne perd aucune miette de leur conversation). C’est-à-dire

• ¬ (M♥ ∧ D♥)
• K_F (¬ (M♥ ∧ D♥))
• K_M (¬ (M♥ ∧ D♥))
• K_D (¬ (M♥ ∧ D♥))
• K_A (¬ (M♥ ∧ D♥))
• mais aussi K_MK_F(¬ (M♥ ∧ D♥))
• K_DK_F(¬ (M♥ ∧ D♥))
• pire : K_DK_MK_F(¬ (M♥ ∧ D♥))

On voit là tout l’intérêt de la notation NP(¬ (M♥ ∧ D♥))...

La règle de DeMorgan permet de réécrire ¬ (M♥ ∧ D♥) sous la forme M♠ ∨ D♠. Comme ce fait est devenu notoirement public, on a

• D♥ ∧ (M♠ ∨ D♠) ⇒ M♠
• K_M(D♥ ∧ (M♠ ∨ D♠)) ⇒ K_M(M♠)
• D♥ ⇒ K_M(M♠)

Or ceci est contradictoire avec l’affirmation de Marc : ¬ K_M(M♥) ∧ ¬ K_M(M♠), de laquelle découle ∧ ¬ K_M(M♠).

On a donc démontré par l’absurde que les mondes 2 et 5 ci-dessus sont également à écarter.

Il ne reste donc que 4 mondes qui puissent modéliser les affirmations de l’énoncé :

1. F♥→M♥→D♠
2. F♥→M♠→D♠
3. F♠→M♥→D♠
4. F♠→M♠→D♠

Ces mondes ont en commun la couleur de la carte de Daniel, laquelle est donc déterminée. Cette couleur devient d’ailleurs de notoriété publique, puisque maintenant que Daniel connaît la couleur de sa carte, tous la connaissent (les deux autres, parce qu’ils l’avaient vue), mais aussi

• K_MK_D(D♠)
• K_FK_D(D♠)
• K_FK_MK_D(D♠)
• K_AK_D(D♠)
• K_AK_FK_D(D♠)
• etc

Par conséquent, la phrase suivante de l’énoncé était superflue :

Daniel affirme alors qu’il connaît, lui, la couleur de sa carte

En résumé :

1. Après la déclaration de Franck, Daniel sait que Franck ne sait pas quelle est la couleur de la carte de Franck ;
2. cela ne permet pas à Daniel de savoir quelle est la couleur de sa carte.
3. Mais Marc aussi, sait que Franck ignore la couleur de la carte de Franck ;
4. Malgré cela, Marc ne sait toujours pas quelle est la couleur de la carte de Marc.
5. Mais Daniel sait que Marc sait que Franck ignore la couleur de sa propre carte ;
6. et comme Daniel sait aussi que Marc ne connaît pas la couleur de sa propre carte, Daniel sait maintenant quelle est la couleur de sa propre carte.
7. Et comme Alain suit tout cela, Alain sait maintenant aussi quelle est la couleur de la carte de Daniel.
8. Alain a un peu le vertige...

Alain et Daniel connaissent maintenant la couleur de la carte de Daniel, et c’est tout. Ils en savent maintenant autant que Marc, qui n’a pas réussi à acquérir de nouvelles informations. Celui qui en sait le plus (et depuis le début), c’est Franck, qui connaît, outre la couleur de la carte de Daniel, celle de la carte de Marc.

On constate que celui qui au début du jeu, avait le moins d’informations sur le jeu, est le seul à pouvoir dire à la fin, la couleur de sa carte. C’est la conséquence du fait que par leurs affirmations, les tricheurs lui ont apporté les informations qu’ils avaient sur la couleur de sa carte, alors que lui ne pouvait, et pour cause, apporter d’information sur la couleur des autres cartes.

La logique épistémique est toutefois insuffisante à elle seule, à expliquer l’évolution des informations lors du dialogue entre agents. On lui substitue de plus en plus d’autres logiques :

• la logique du dialogue
• la logique des questions
• la logique doxastique, où à la notion de connaissance (non révisable parce que nécessairement vraie), on substitue celle de croyance révisable à la lumière de nouvelles informations : On peut croire à quelque chose de faux.

C’est une démarche voisine que celle initié par Thomas Bayes, qui, en donnant à chaque croyance un poids (ici, sa probabilité), permet de voir comment évoluent les croyances des agents lors des différentes phases du dialogue entre eux. L’inférence bayésienne consiste à évaluer comment les différentes déclarations des agents, modifient les probabilités des différents mondes vus ci-avant. Tout d’abord, on leur attribue des probabilités a priori, et ensuite, chaque affirmation d’un agent mène à leur remplacement par des probabilités conditionnelles.

Probabilités a priori

Toutes les probabilités auront pour dénominateur la factorielle de 5, soit 120, puisque c’est le nombre de manières d’ordonner les 5 cartes avant d’en distribuer 3.

• Le monde F♥→M♥→D♥ a bien entendu une probabilité nulle puisqu’il n’y a en tout que deux cartes rouges dans le jeu complet.
• F♥→M♥→D♠ peut être obtenu de 6 (nombre de façons de permuter les 3 cartes noires) fois 2 (nombre de manières de permuter les deux cartes rouges) soit 12 manières possibles ; sa probabilité est donc 12/120=1/10=0,1.
• F♥→M♠→D♥ et F♠→M♥→D♥ sont également de probabilité 1/10=0,1.
• F♥→M♠→D♠ est défini par le choix d’une carte rouge distribuée à Franck (deux possibilités) et de deux cartes noires (parmi trois : 3 possibilités) distribuées à Marc et Daniel. Ce nombre de possibilités doit être multiplié par 2 (échange de la carte rouge et de la carte noire non distribuées) et encore par 2 (on ne change pas la configuration en échangeant les cartes de Marc et Daniel) ; soit 24 possibilités ; donc sa probabilité est 24/120=⅕=0,2.
• F♠→M♥→D♠ est aussi de probabilité ⅕
• F♠→M♠→D♥, aussi a pour probabilité ⅕.
• F♠→M♠→D♠ est de probabilité 1/10 puisqu’il y a 6 manières de ranger les cartes noires, fois deux manières de ranger les deux cartes rouges non distribuées.

On vérifie que 0,1+0,1+0,1+0,2+0,2+0,2+0,1=1 comme il se doit.

Probabilités modifiées par l’annonce de Franck

Comme on parle de probabilités, on ne notera plus la conjonction « et » par un ∧ mais par la notation probabiliste ∩.

L’annonce de Franck est liée à l’évènement conditionnant M♠ ∪ D♠ ; la probabilité de cet évènement est 0,9 d’après les résultats ci-dessus (la probabilité de son contraire est 1/10). D’après la définition des probabilités conditionnelles, les probabilités ci-dessus sont divisées par 9/10, soit

1. F♥→M♥→D♠ n’est plus de probabilité 1/10, mais maintenant sa probabilité a augmenté ; elle est passée à 1/9.
2. F♥→M♠→D♥ voit aussi sa probabilité passer de 1/10 à 1/9 ;
3. mais F♠→M♥→D♥ est maintenant de probabilité (conditionnelle) nulle.
4. F♥→M♠→D♠ voit sa probabilité passer de ⅕ à 2/9.
5. F♠→M♥→D♠ est aussi de probabilité 2/9 maintenant.
6. F♠→M♠→D♥, aussi a pour probabilité 2/9.
7. F♠→M♠→D♠ voit sa probabilité passer de 1/10 à 1/9, une augmentation donc.

Probabilités modifiées par l’annonce de Marc

Par son annonce, Marc change à nouveau l’univers de probabilité, l’évènement conditionnant étant le contraire de M♠ ∩ D♥. Ce dernier est la réunion des deux évènements 2 et 6 ci-dessus, et leur probabilité va donc devenir nulle ; de plus, ils sont disjoints et la probabilité de leur réunion est 1/9+2/9=⅓. La probabilité de l’évènement conditionnant (qui est la réunion des évènements 1,3,4,5 et 7) est donc 1-⅓=⅔. Chacun de ces évènements va donc voir sa probabilité divisée par ⅔ ; soit

1. F♥→M♥→D♠ dont la probabilité 1/10 est passée à 1/9, a comme nouvelle probabilité ⅙.
2. F♥→M♠→D♥ voit sa probabilité devenir nulle (incompatible avec l’évènement conditionnant) ;
3. mais F♠→M♥→D♥ reste de probabilité nulle.
4. F♥→M♠→D♠ dont la probabilité était passée de ⅕ à 2/9, est maintenant passée à ⅓.
5. F♠→M♥→D♠ est aussi de probabilité ⅓ maintenant.
6. F♠→M♠→D♥, est maintenant impossible (ou plutôt incompatible avec l’évènement conditionnant).
7. F♠→M♠→D♠ voit sa probabilité passer de 1/9 à ⅙.

Par addition, on peut donc en déduire la probabilité des couleurs des cartes de chacun :

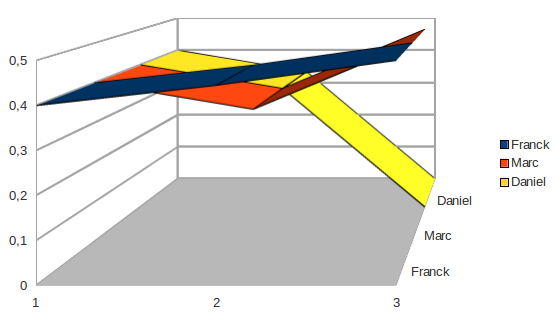
• P(F♥)=⅙+⅓=½ (mais après être passée à 4/9 après l’annonce de Franck) ;
• Donc P(F♠)=½ aussi (après être passée à 5/9 lors de l’annonce de Franck).
• P(M♥)= ⅙+⅓=½ (sa valeur initiale était ⅖ comme pour les autres, et elle était passée à ⅓ lors de l’annonce de Franck ; elle n’a donc fait qu’augmenter lors des différentes annonces).
• P(M♠)=½ (mais comme elle valait ⅗ au début, elle a décru en commençant même par augmenter à ⅔).
• P(D♠)=1 (valeur initiale : ⅗ puis après l’annonce de Franck, ⅔).
• P(D♥), initialement égale à ⅖, est descendue à ⅓ après l’annonce de Franck, pour finalement chuter à 0 après l’annonce de Marc.

Voici l’évolution temporelle des probabilités que la carte de chacun soit rouge :

et l’évolution des probabilités que la carte de chacun soit noire :