Le calcul par le caviar

lundi 11 mai 2015
par  Alain BUSSER

Ce jeu est similaire au jeu de la vie et au jeu des alligators, par les points suivants :

  • Il s’agit d’un jeu de vie artificielle ;
  • C’est un jeu à zéro joueur ;
  • Ce jeu est Turing-complet.

En effet il s’agit d’un système de tague d’Emil Post, apparu en plusieurs étapes (1921, 1943 et 1947) dans les travaux que celui-ci consacrait au problème du mot.

théorie du jeu
Simulation de tag-systems en ligne, et en CoffeeScript
Alain Busser 2015
le jeu en ligne avec animations
c’est en touchant qu’on apprend
Alain Busser 2015

historique de la notion

Ces travaux, largement antérieurs à la construction des premiers ordinateurs, viennent de l’algèbre, et plus particulièrement la théorie des groupes [1].

La vie est-elle un système de tague ?

Non [2].

Le jeu parle donc de poissons pondant des œufs : C’est un jœufs ! Au début du jeu, on a une population initiale d’œufs appelée axiome [3]. Ci-dessous ce sont les 6 œufs bleus posés sur le sable en-dessous de l’eau. En effet la moitié supérieure de l’écran est un aquarium dans lequel évoluent les poissons.

Dans le sable, on voit une sorte de poste (!) de pilotage, essentiellement formé d’un tableau. Celui ci-dessus indique que

  • lorsqu’un poisson bleu pond, c’est toujours un œuf rouge suivi d’un œuf vert [4] ;
  • lorsqu’un poisson rouge pond, c’est juste un œuf bleu [5] ;
  • lorsqu’un poisson vert pond, c’est toujours trois œufs bleus [6].

Mais ce n’est pas tout : Lorsqu’un œuf éclot, il donne naissance à un poisson de la même couleur que lui, et celui-ci va pondre ses œufs tout à droite. Et en plus, lorsqu’un œuf éclot, il détruit un certain nombre de ses voisins dans l’explosion [7]. Enfin, un volcan sur la gauche amène juste assez de chaleur pour permettre à l’œuf le plus à gauche d’éclore en premier.

Définir un micromonde se fait donc en modifiant les règles de reproduction, ainsi que la population initiale (ou axiome).

Collatz

En fait, l’exemple ci-dessus simule la suite de Collatz [8]. Voici comment on peut le programmer en Bourne-Again shell :

axiom='bbb'
while [ ${#axiom} -gt 1 ]
do
    eggs=${axiom:0:2}
    case ${eggs:0:1} in 
        'b')
            axiom=$axiom'rv';; 
        'g')
            axiom=$axiom'b';; 
        'v')
            axiom=$axiom'bbb';; 
    esac
    axiom=${axiom#$eggs} 
    echo $axiom 
done

Le symbole « dollar » placé devant le nom d’une variable, donne sa valeur. Mais si après le nom de la chaîne de caractères on met des nombres il y a découpage ; et si on met le symbole « dièse » on obtient la longueur de la chaîne. gt signifie « greater than » et esac clôt les tests case. Enfin la concaténation est notée le plus simplement du monde...

On va voir ci-dessous comment on peut modifier le jeu pour qu’il simule le problème de Post (1921). Tout d’abord on actionne les curseurs pour que

  • Il n’y ait plus que deux couleurs donc plus que deux règles ;
  • Le rayon d’action de l’explosion-éclosion d’un œuf soit 3 et non 2 (l’œuf détruit 2 voisins en éclosant).

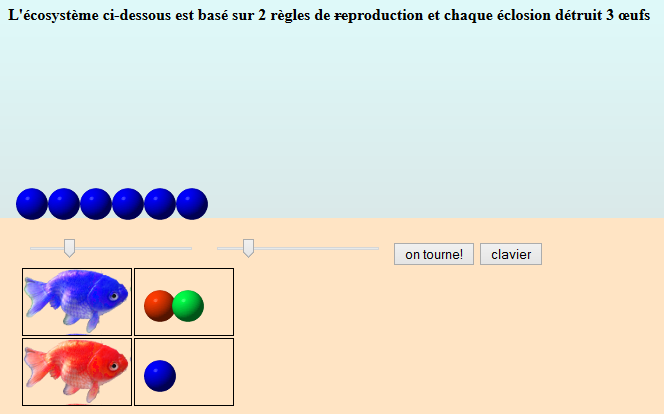
On voit que le tableau ne comporte plus que deux lignes, le poisson vert ayant disparu. Maintenant on voudrait que le poisson bleu ponde deux œufs. On peut ajouter des œufs à la règle de production en les faisant glisser du bas de l’écran vers l’entrée du tableau choisie, mais on doit d’abord enlever les œufs rouge et vert, ce qu’on fait en tapant deux fois sur le poisson bleu (chaque « tap » enlève le dernier œuf) :

Ensuite on fait glisser deux fois de suite l’œuf bleu en bas vers la case devenue vide du tableau :

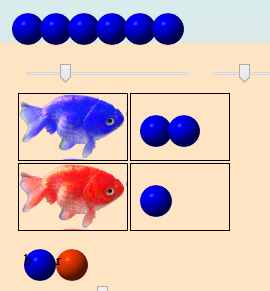
Pour le poisson rouge, la pondaison est plus prolifique et plus multicolore : Deux œufs rouges, un œuf bleu et un troisième œuf rouge. Donc, un tap sur le poisson rouge pour enlever l’œuf bleu, puis on fait glisser successivement l’œuf rouge deux fois, l’œuf bleu et encore l’œuf rouge :

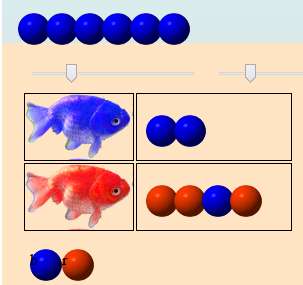
Cet écosystème a une évolution dépendant grandement de l’« axiome » c’est-à-dire de la configuration des œufs bleus et des œufs rouges initiale. Par exemple la population oscille si sa configuration initiale est formée de trois œufs bleus suivis d’un œuf rouge. Pour enlever le dernier œuf de l’axiome, il suffit de le casser en tapant dessus :

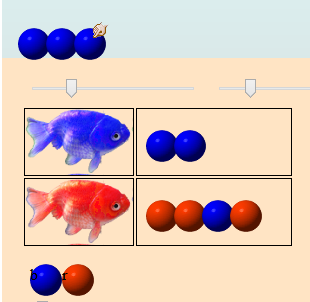
Une fois qu’il ne reste plus que 3 œufs bleus, on fait glisser l’œuf rouge du bas (marqué « r ») vers l’axiome pour enrichir celui-ci d’un œuf rouge :

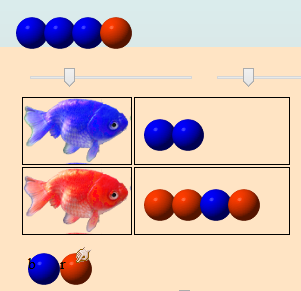
Maintenant on peut jouer. En touchant l’eau (pas l’axiome, au-dessus de celui-ci) on déclenche une éruption volcanique qui fait éclore l’œuf de gauche. Comme celui-ci est bleu il en sort un poisson bleu pendant que l’œuf et ses deux voisins se désagrègent :

Ce poisson va alors, comme il a été programmé pour cela, pondre deux œufs bleus après l’œuf rouge, ce qui ne suffit pas à compenser la perte des trois œufs bleus, et la population est maintenant en danger :

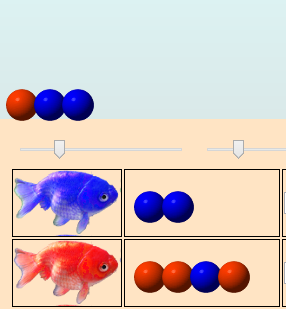
Ensuite, le poisson bleu file vers la droite de l’écran, et quitte cette zone volcanique sous-marine. Si ensuite on tape à nouveau sur l’aquarium, c’est l’œuf rouge qui va éclore puisqu’il est tout à gauche. Il va donc donner naissance à un poisson rouge :

Heureusement d’ailleurs, parce que les trois œufs ayant été détruits dans l’éclosion, il n’y a plus d’œuf. Mais le poisson rouge pond 4 œufs :

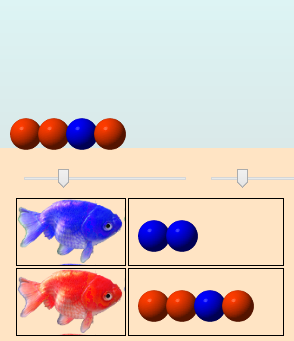
Le premier d’entre œufseux est rouge, il en sort donc un poisson rouge :

La population augmente donc à nouveau :

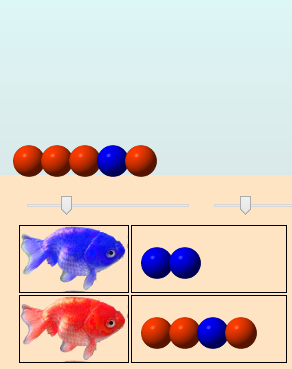
D’autant que le premier œuf étant toujours rouge, il en sort à nouveau un poisson rouge :

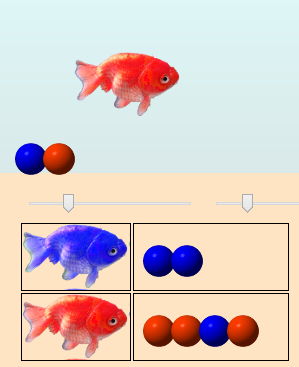
On arrive à une population de 6 œufs :

Mais cette fois-ci le poisson qui sort est bleu :

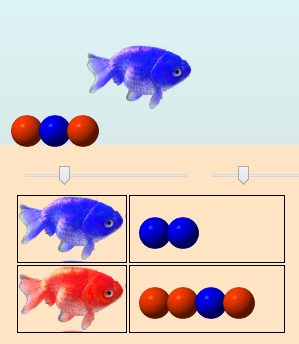
ce qui fait redescendre la population à 5 œufs :

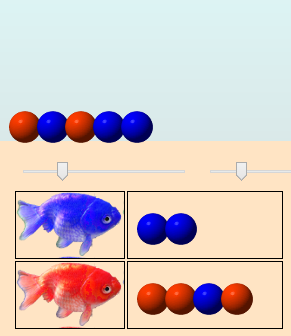
Le poisson suivant est donc rouge :

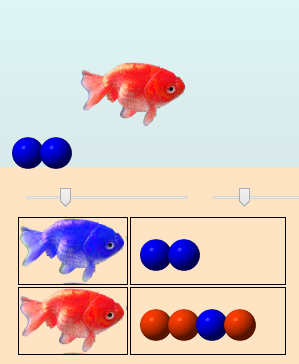
La population repasse alors à 6 œufs :

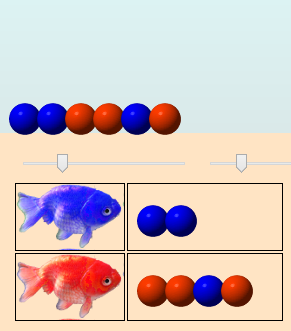
Mais le poisson suivant est bleu :

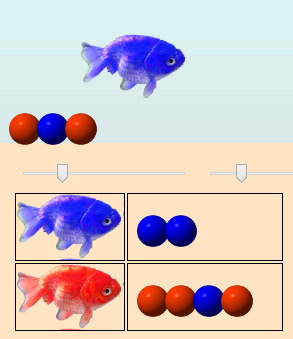
La population obtenue est la même que l’avant-dernière :

La population est donc finalement périodique de période 2, donc ne risque plus de s’éteindre. D’autres populations s’éteignent comme par exemple celles ne comportant que des œufs bleus. Saurez-vous en trouver d’autres ?

version bash

Ici on ne sait pas si la boucle finit alors on boucle 20 fois, pour voir :

axiom='rrbrbr'
for n in <span class="base64" title="PGNvZGUgY2xhc3M9InNwaXBfY29kZSBzcGlwX2NvZGVfaW5saW5lIiBkaXI9Imx0ciI+c2VxIDEgMjA8L2NvZGU+"></span>; do
    egg=${axiom:0:3} 
    case ${egg:0:1} 
        'b')
            axiom=$axiom'bb';; 
        'r')
            axiom=$axiom'rrbr';; 
    esac
    axiom=${axiom#$egg} 
    echo $axiom 
done

Turing

En fait, il résulte d’un théorème de Wang (1963) que les tague systèmes de Post sont Turing-complets (à l’exception des 0-tags ou des 1-tags). Ainsi, on peut simuler un système de tague avec une machine de Turing : Le poisson, dont l’état interne est représenté par sa couleur actuelle, et qui agit sur une bande représentée par le caviar. Dans ce cas le nombre d’états visible est égal au nombre de symboles (les couleurs).

Dans le jeu ci-dessous, il y a 7 couleurs possibles (donc 7 règles de production possibles) :

couleurs symboles
bleu b
rouge r
vert v
magenta m
cyan c
jaune j
noir n

On peut enregistrer ou communiquer un micromonde par des chaînes de caractères, en ouvrant le clavier (en appuyant un nombre impair de fois sur le bouton idoine) et en copiant-collant les chaînes de caractères obtenues (attention : Elles se mettent à jour lors de l’évolution de l’écosystème) .

La version du jeu en ligne ci-dessous utilise le clavier [9] pour entrer ou modifier les règles et l’axiome : toucher le bouton « clavier » puis programmer un micromonde afin de l’explorer :

Calculviar

L'écosystème ci-dessous est basé sur 3 règles de reproduction et chaque éclosion détruit 2 œufs

          Conclusion provisoire

          • Il est possible de transformer ce jeu à 0 joueur en un jeu à un joueur (« réussite » ou « solitaire (patience) »), en donnant une population à atteindre et en demandant au joueur la population initiale permettant d’arriver à cette population « finale ». On peut même en faire un métajeu en demandant également pour quelles règles de production on peut arriver à ce but [10]
          • Pour les enfants les plus tactiles, les œufs peuvent être représentés par des perles de différentes couleurs et on peut jouer sur un collier, par exemple pour le problème de Post ci-dessus, à chaque tour de jeu, on enlève les 3 perles de gauche, on regarde la couleur de la plus senestre d’entre elles, et si elle est bleue on enfile 2 perles bleues à droite, sinon on enfile une rouge, une bleue et deux rouges. Avec des perles de grande taille sur des barres de métal, le PE peut « afficher » les règles au tableau. La version individuelle est assez bon marché avec des perles de plastique comme on en vend pour les petites filles.
          • Les enfants aveugles peuvent jouer aussi si les perles sont de forme ou de taille différente.
          • Le jeu est praticable sitôt que l’enfant distingue les couleurs et sait compter jusqu’à 4, donc a priori assez jeune.
          • La version logicielle ci-dessus permet de modifier les règles pendant qu’on joue, ce qui va beaucoup plus loin que l’imaginait Post, en particulier avec la notion, non encore explorée à ce jour, de système de Post non déterministe...

          Addendum

          Les nouveaux programmes de collège incitent à faire programmer par les collégiens ce genre de système, de préférence avec un outil de programmation graphique. Voici la version Sofus :

          La grammaire transformationnelle est codée par un bloc fait de tests sur la prémisse et de conclusions à retourner dans chaque cas :

          Pour programmer le système de Post, on répète les opérations suivantes :

          • Ajouter à la fin du mot r, le suffixe calculé par la fonction tag appliquée à la première lettre du mot r ;
          • enlever les trois premières lettres de r se fait en remplaçant r par le mot commençant à la quatrième lettre et finissant à la fin ;
          • il n’y a plus qu’à ajouter le nouveau mot r en bas de l’affichage.

          En Sofus, tout le programme est ici :

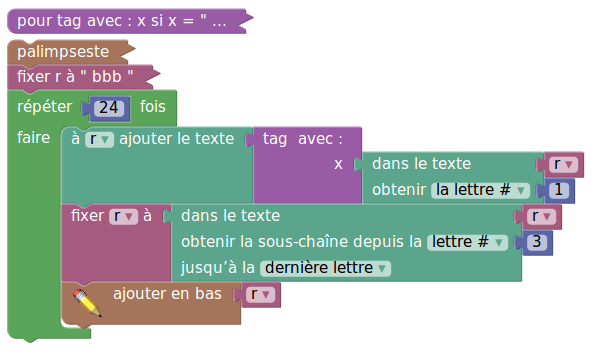
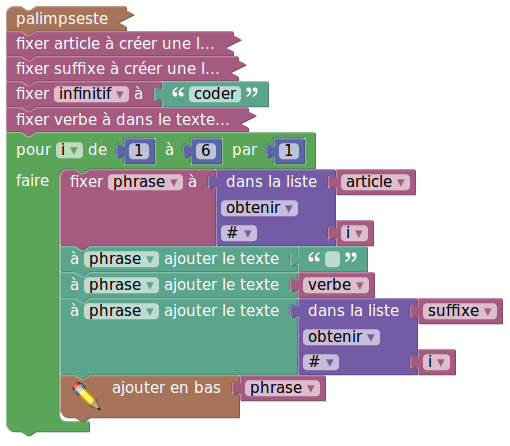
          En fait, on peut même réaliser un logiciel de conjugaison à l’aide de ces techniques de découpage [11]. La fonction tag vue ci-dessus permet aussi de se lancer dans la cryptographie : On boucle sur les lettres du mot et on « tague » chacune par un texte qui va constituer le mot codé. Mais en dehors des babas fans du groupe Abba, on en vient vite à chercher des méthodes de cryptage plus efficaces que la fonction définie lettre par lettre.


          [1] Suivant les recherches de Thurston sur la géométrie hyperbolique en dimension 3, on considère par exemple les matrices U et V suivantes :

          On vérifie par le calcul que le carré de la première matrice est le cube de la seconde. Ceci permet de simplifier des produits des matrices U et V comme UUVUVVVVUUV (en remplaçant par exemple VVV par UU). Il y a une centaine d’années, Axel Thue demandait s’il y avait un moyen de savoir sans effectuer les produits de matrices, si deux produits du type UUVVUVUUVVVUV et VVUVUUVVU sont égaux : Thue cherchait un algorithme permettant de comparer des produits de matrices. Cette question est connue sous le nom de problème du mot. Les opérations comme le remplacement de VVV par UU s’appellent des règles de réécriture. Le problème du mot a été un des sujets de recherche d’Alan Turing dans les années 1950. Mais dès le début des années 1920, Emil Post s’est intéressé au cas particulier des « systèmes semi-thuéens » (problème du mot pour les semi-groupes, cas où les matrices ne sont plus forcément inversibles). C’est dans le cadre de ces réflexions sur un problème de nature algébrique que Post a inventé le problème exposé ci-dessus.

          Emil Post était logicien, il cherchait avant tout à modéliser l’évolution des états internes d’un logicien lors de la rédaction d’une démonstration mathématique en logique propositionnelle : Une démonstration n’est jamais qu’une manipulation de chaînes de caractères, comme remplacer p∧(p ⇒ q) par p∧q. Aussi dans ces jeux de manipulation de chaînes de caractères, on appelle

          • axiome la chaîne de caractères initiale ;
          • règles (de production, pas de déduction) les étapes de l’algorithme appliqué à la chaîne de caractères) ;
          • théorèmes les productions successives (chaînes de caractères obtenues).

          Par la suite, Post est passé à autre chose, mais à la fin de la seconde guerre mondiale, presque en même temps et indépendamment l’un de l’autre, Emil Post et Andreï Markov (mathématicien soviétique) ont montré que les systèmes de réécriture sont Turing-complets.

          Une dizaine d’années plus tard, presque en même temps et indépendamment l’un de l’autre, Stephen Cole Kleene et Noam Chomsky ont fondé la théorie des langages sur des notions similaires, le théorème de Kleene et la grammaire générative et transformationnelle, respectivement.

          Avec l’algèbre, la logique, la calculabilité et la théorie des langages, le problème de Post est donc central en informatique théorique.

          [2] car, alors qu’un système de tague modifie in situ une chaîne de caractères, la biosynthèse des protéines est effectuée par des ribosomes qui lisent une chaîne de caractères (l’ARN messager) et écrivent une autre chaîne de caractères (la protéine). pour autant,

          • la construction de la protéine par le ribosome est analogue au jeu ci-dessus, en assimilant les acides aminés aux perles qui sont pondues sur la droite de la figure (l’axiome représentant la protéine) ;
          • le ribosome étant lui-même fait d’acides nucléiques, est « écrit » dans la même langue que la chaîne de caractères qu’il lit (un peu comme dans le jeu ci-dessous) ;
          • la notion d’étiquette (biologie) est similaire à l’ajout de lettres à la fin d’un mot ; on touche là à la bioinformatique...
          • voir la typogénétique d’Hofstadter aussi.

          [3] le mot est d’Emil Post, logicien, qui voulait ainsi modéliser le travail d’un logicien en train de rédiger les étapes successives d’une démonstration

          [4] cela a pour effet de colorier la rangée d’œufs bleus alternativement en rouge et en vert, ce qui a à son tour pour effet de représenter par la couleur du premier œuf, la parité du nombre total d’œufs

          [5] cela a pour effet de diviser par 2 le nombre d’œufs bleus, cette division ne se faisant que si le premier œuf est rouge, c’est-à-dire si le nombre d’œufs bleus était pair

          [6] ce qui multiplie par 1,5 le nombre d’œufs bleus si celui-ci était impair, c’est-à-dire si le premier œuf était vert

          [7] ici, le voisin de droite, c’est donc un 2-tag system puisque 2 œufs disparaissent à l’éclosion : Celui qui a éclot et son voisin.

          [8] d’après un algorithme de Liesbeth de Mol

          [9] parce que la programmation sans clavier utilise jQuery-UI qui entre parfois en conflit avec spip, et que cet article est rédigé en spip. La version en ligne n’utilise que jQuery, pas jQuery-UI...

          [10] On peut aussi chercher des configurations non atteignables comme un Jardin d’Éden (automate cellulaire).

          [11] Pour les verbes du premier groupe, on

          • extrait la racine verbale du verbe, en enlevant le « er » final, ce qui se fait en gardant le mot (initialement à l’infinitif) privé de ses 2 dernières lettres ;
          • boucle sur les personnes, en créant une phrase formée de
            • l’article (en fait un pronom) ;
            • un espace séparant l’article du verbe
            • la racine verbale
            • la terminaison (suffixe)

          Pour se faciliter la vie, on crée une liste de sujets (article) et une liste de terminaisons (suffixe) :

          Pour avoir la racine verbale on découpe le verbe à l’infinitif :

          Enfin la constitution de la phrase se fait à la façon Sofus, en ajoutant progressivement des morceaux de phrase par concaténations successives :

          On peut aussi demander le verbe par une entrée textuelle. Cela permet d’avoir des variantes comme

          je programme
tu programmes
elle programme
nous programmons
vous programmez
elles programment

          Prolonger cette activité à des verbes des groupes 2 et 3 est un exercice intéressant sur les tests (sur l’avant-dernière lettre du verbe à l’infinitif).


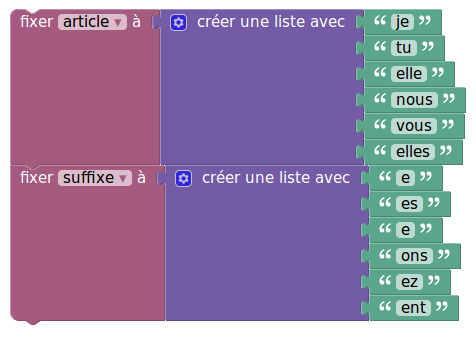
          Commentaires