Analyse de la géométrie du cycle 3 par ERMEL

ERMEL est une Equipe de Recherche pour l’enseignement des Mathématique à l’école ELémentaire de l’INRP. Ce paragraphe reprend, de manière succincte, l’analyse théorique (de 80 pages) que propose ERMEL pour la géométrie du cycle 3, dans son ouvrage de 2006.

Cet onglet est constitué - pour l’essentiel - d’extraits de la partie théorique de l’ouvrage ci-contre.

Pour l’équipe ERMEL, si la géométrie du cycle 3 est une géométrie instrumentée, c’est pour faire vivre une géométrie des propriétés des objets : les instruments sont des outils qui permettent une validation par les propriétés.

L’équipe ERMEL présente d’abord la géométrie comme une modélisation du monde sensible. Le travail géométrique en cycle 3, même s’il est encore imbriqué avec le monde sensible dans lequel l’élève évolue, par le rôle décisif du langage, participe à l’élaboration d’un « savoir géométrique » sur les figures qui sont, pour ERMEL, des « objets de pensée ». On s’inscrit ici dans une approche platonicienne de la géométrie, celle des figures idéales, approche classique et relativement mythique sur laquelle les historiens des mathématiques sont plus nuancés (Tournès).

L’équipe ERMEL pointe en particulier une différence essentielle entre le cycle 2 et le cycle 3 en terme de capacité d’anticipation sur les objets de l’espace. Au cycle 2 on reste dans une approche concrète de l’espace. Les tâches, accomplies dans l’action, n’ont aucune capacité d’anticipation (*) alors qu’au cycle 3, les situations concrètes sont modélisées par des représentations d’objets idéalisés sur lesquels - par les situations proposées - il va être nécessaire d’anticiper, en particulier avec l’usage des instruments ou des propriétés géométriques.

(*) Nuance sur l’anticipation

Exemple d’anticipation sur l’espace en cycle 2

Cette question (capacité d’anticipation des élèves) semble être une des lignes directrices de Roland Charnay dans l’élaboration de la collection CAP Maths. On pense, en géométrie, à ses activités d’introduction du quadrillage (travail sur le message en CP) et en particulier à cette activité d’anticipation sur les points de vue en CE1 - les 3 cônes ci dessus - qui tente, même partiellement sur une ingénierie spécifique, d’infirmer cette constatation générale.

Dessins, figures et représentations

Tout d’abord on distingue deux types d’objets ceux du monde sensibles et ceux de la modélisation, les objets « idéaux » ou objets géométriques. D’une manière générale, l’équipe ERMEL parle de dessin quand il y a trace par un outil dans un espace graphique. Il cite les traces de Socrate dans le sable, l’environnement papier crayon, et l’environnement numérique : logiciel-écran d’ordinateur. Les figures sont alors des objets de la géométrie euclidienne, ce sont des constructions de l’esprit, décrites par un texte, une formulation, ou des propriétés. Une figure est alors représentée dans un espace graphique (dessin) ou dans le monde sensible (maquette).

En géométrie dynamique (GD dans la suite), le « dessin » de l’écran est une instance de la figure. L’élève manipulant les points de base de la représentation graphique, agit sur des instances de la figure pour vérifier, selon les cas, sa résistance à la déformation ou au contraire observer des invariants. L’hypothèse que la GD modifie sensiblement le rapport aux figures a été longuement étudiée depuis 1990, soit depuis 20 ans. Désormais il est reconnu, y compris dans les programmes scolaires, que le GD est un nouveau paradigme pour l’enseignement de la géométrie (Michèle Artigue - Colloque DEGESCO - Février 2007).

Les constituants des savoirs géométriques

Pour ERMEL, ces constituants s’organisent en trois niveaux :
– Les objets : ils peuvent être matériels, du monde sensible, comme des gabarits de rectangle, de carrés, de losange ... ou théoriques (« géométriques »), comme les points ou les droites, mais aussi carré, rectangle, losange ... comme figures idéales.
– Les relations : ce sont les liens entre les objets. Il y a tout d’abord le parallélisme et l’orthogonalité (pour les droites), puis l’appartenance. Ensuite l’égalité de longueur. ERMEL place aussi à ce niveau le repérage, l’isométrie et la similitude.
– Les énoncé ou propriétés : ce sont les liens entre objets et relations. En pratique ces énoncés peuvent se présenter sous la forme d’une propriété d’un objet (le cube a 8 sommets) ou de ce qui sera plus tard un théorème comme la transitivité du parallélisme.

L’ouvrage de ERMEL étant orienté vers la résolution de problème, les énoncés au cycle 3 sont essentiellement présentés sous trois aspects :
– Ils peuvent être implicitement contenus dans certaines méthodes de construction.
– Ils sont d’abord des solutions implicites de certains problèmes. Typiquement « Est-il possible de construire un triangle avec deux angles droits ».
– Ils sont aussi des outils pour valider une solution, en particulier quand la perception ne permet pas de conclure.

Les énoncés mathématique au cycle 3 sont du côté des outils, ce ne sont pas des objets d’étude en soi.

La question de la validation

La validation pratique, opérationnelle, a de nombreuses limites quand on commence à vouloir être précis. Une des premières limites est la relation entre une procédure et son exécution : quand il y a invalidation, laquelle est invalidée ?

Pour certains cette question est un des aspects à considérer pour rendre compte d’un certain rejet de la pratique géométrique en classe. Dans certaines classes cette difficulté formerait un consensus pour ne pas aller au dela dans les constructions géométriques dans le monde sensible, physique.

Un seconde limite de la validation pratique est la difficulté de formulation et de critique des procédures de résolution. C’est une situation générale mais que l’on voit plus particulièrement quand il faut rendre compte d’actions ou de gestes fugaces dont on n’a pas toujours conscience.

On verra un peu plus loin que la pratique de la GD n’exclu pas cette difficulté de gestes fugaces dont on n’a pas conscience. Seulement dans ce cadre, il est beaucoup plus facile pour le maitre d’anticiper avec précision ces gestes et il est facile de les faire reproduire individuellement ou collectivement.

Ces deux points - un fois observés en classe par les élèves - permettent d’installer un passage à une validation organisée autour des propriétés, par l’intermédiaire du débat. ERMEL dégage deux arguments :
– Le débat pousse à l’explicitation de ce à quoi l’action ou la perception ne permet pas de dégager.
– Les élèves ont alors recours à un langage qui les libère (en partie) de l’action, et sollicite d’autres types de validations, tout en participant à la conceptualisation du vocabulaire géométrique utilisé.

L’équipe ERMEL insiste alors sur le rôle décisif du langage dans l’évolution des preuves :
– Il permet la distinction des différents types de preuves (action, mesure, images mentales, usage des propriétés)
– Et les distinguer des « preuves élèves », en particulier l’évidence construite sur l’expérience sociale et la connaissance partagée.
– Il permet de reconnaitre le statut différent des critères engagés, qu’ils soient techniques ou mathématiques.

Il ne faut pas minimiser les difficultés de ce passage d’une validation « par l’évidence de l’action », si efficace au cycle 2, à une validation par l’utilisation de propriété des objets. Tout comme il y a en arithmétique un décalage temporel important dans les procédures de l’addition comme objet ou comme outil, on retrouve ici ce décalage temporel entre l’utilisation des propriétés en acte et leur disponibilité comme savoir dans des débats argumentés. On sait qu’il peut y avoir de 1 à 2 ans de décalage sur le simple prolongement d’un trait, c’est-à-dire la transformation d’un segment en droite. Nous verrons das les onglets suivants en quoi la pratique de la géométrie dynamique peut être un facteur accélérant dans certaines situations.

D’une manière générale ERMEL mentionne que la validation en géométrie fait appel à des procédures plus théorique que dans le registre numérique, de part sa mise en mots plus complexe, l’utilisation d’un vocabulaire spécifique, mais qui prend aussi tout son sens.

Il y a bien entendu beaucoup d’autres développements dans la première partie de l’ouvrage d’ERMEL, nous n’avons retenu que quelques fils directeurs.

Les figures en géométrie dynamique

Les sorties graphiques (1) produites par un logiciel de géométrie dynamique sont certes des dessins dans un espace graphique, mais surtout, parce qu’elles sont manipulables, des instances de la figure géométrique envisagée. Comme telles les relations entre les objets doivent résister au mouvement des points de base. Ainsi un rectangle désigné comme tel doit rester à l’écran un rectangle dans la manipulation : les propriétés du rectangle doivent être conservées, et donc les relations entre les objets de base, définissant le rectangle doivent être conservées

On voit qu’utiliser la géométrie dynamique va obliger à certaines contraintes dont celle de travailler tout de suite en terme de relations entre les objets - ici orthogonalité des côtés adjacents - et des propriétés des objets, par exemple qu’un rectangle est un quadrilatère ayant 4 angles droits.

Les propriétés implicites apparaissent très vite aussi en GD

On comprend du même coup la pertinence de l’analyse d’ERMEL pour ce qui est des propriétés : elles sont toujours implicitement présentes dans les construction, et ce sera de la vigilance de l’enseignant de rester dans l’objectif des programmes et ne pas aller au delà, en particulier de laisser ces propriétés du côté des outils, et ne pas les regarder comme des objets d’étude : cela ne peux pas se faire avant la classe de 4°, même si on argumente avec ces propriétés comme outils à partir de la classe de 6°.

Toujours sur l’exemple de la construction d’un rectangle, en supposant acquis que des droites sont parallèles si elles ont une perpendiculaire commune, définition courante en CE2 que l’on travaille par exemple par pliages successifs (2), alors la construction d’un rectangle consiste à prendre une seconde perpendiculaire à deux droites parallèles. On voit que l’on active - implicitement donc - des propriétés sur l’orthogonalité et le parallélisme (3) (ici qu’une perpendiculaire à une droite est perpendiculaire à toute parallèle à cette droite) qui ne sont qu’au programme de 6°, en tant que propriétés utilisable pour argumenter.

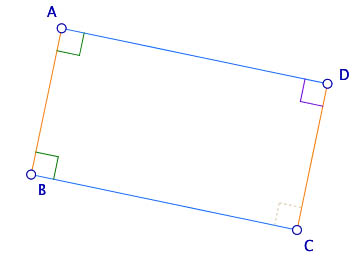
Puisque la définition du rectangle est d’avoir 4 angles droits, il faut valider l’orthogonalité en C. Avec un logiciel de GD on dispose d’outils de tests, dans l’environnement papier crayon, on vérifie à l’équerre ou au gabarit d’angle droit. Dans les deux cas on valide, avec un outil, du monde sensible ou logiciel, que le quatrième angle est droit, et donc que le quadrilatère ainsi construit est un rectangle : on est bien dans une géométrie instrumentée, les instruments servant à vérifier les propriétés des objets.

La validation du 4° angle droit est donc instrumentale. Par contre, en CM2, on peut envisager de proposer des tâches d’argumentation sur le fait que si on a construit (4) trois angles droits, alors on sait, par les relations entre les objets, que les côtés opposés sont deux à deux parallèles car on a deux paires d’angles droits, en A et B puis en A et D : on a donc mis en évidence une propriété du rectangle.

On voit bien qu’ici peuvent intervenir des « preuves élèves » qui mettent en jeu le savoir social (« c’est comme cela qu’on fait un rectangle »), ou l’évidence de la construction. Elles peuvent par exemple se traduire par des affirmations du type « comme c’est un rectangle alors le 4° angle est droit », type d’affirmation encore très prégnante en fin de collège, et qui est exactement, en logique, la réciproque de ce qu’il faudrait montrer si on voulait faire une preuve.

Que serait alors une démarche de type « objet d’étude » sur l’orthogonalité en D ?

Réflexion pour la formation

Ce qui suit n’a aucun sens ni en primaire, ni même au collège, mais on peut envisager de le proposer en formation des enseignants sur le logiciel, pour manipuler les outils, et réfléchir sur les questions d’incidence en géométrie plane.

Le contexte : à partir d’une droite (AB) on construit (5) deux perpendiculaires à cette droite en A et B puis à partir d’un point D de cette droite perpendiculaire passant par A, on construit la perpendiculaire à (AD) en D, elle coupe la parallèle à (AD) en C.

Au lieu de tester si l’angle en C est droit par un outil de vérification de conjecture, on peut aller plus loin et par exemple :

– construire la perpendiculaire à (BC) issue de D et voir si C appartient à cette droite : alors les droites sont confondues.
– construire la perpendiculaire en C à (AD) et appeler E l’intersection avec (AD), puis tester si E est confondu avec D.
Dans les deux cas on voit bien que l’on est dans un contexte fortement axiomatisé car, pour conclure, on utilise dans tous les cas des caractérisations d’incidence, à savoir que par deux points il ne passe qu’une seule droite.

Il est clair qu’une telle démarche n’est pas accessible au collège.

La relation entre les objets comme invariant résistant au mouvement

Ainsi, en géométrie dynamique, on s’extrait du contexte de la simple représentation statique des figures de l’environnement papier-crayon en y ajoutant cette contrainte d’une nécessité de respecter les relations entre les objets - voire leurs propriétés - pour que la figure produite résiste au mouvement.

Dans CaRMetal, il y a même un outil pour « secouer la figure » afin que l’élève puisse vérifier lui-même cette résistance au mouvement.

Un exemple de l’utilisation du Monkey

Dans cet extrait de 8 s, on voit (plus ou moins car la figure est petite) que le carré orange - qui est un vrai carré - est non déformé dans le mouvement aléatoire alors que le carré perceptif bleu, lui est toujours déformé dans le déplacement aléatoire des points

Même si on peut ne pas être tout à fait d’accord avec le fait d’être encore face à un dessin comme l’affirme ERMEL, il est clair en revanche que cette nouvelle contrainte ne fait que reculer la représentation des figures, elle n’aboutit évidemment pas spontanément au concept de figure géométrique au sens de Platon. Ce qui fait la force de la GD et de sa manipulation directe est que la nouvelle représentation embarque nécessairement beaucoup plus de géométrie que le contexte papier-crayon dans lequel la pratique scolaire, de fait - par des reproductions de dessins, des mesures - installe ce qui voudrait être des constructions géométriques dans des pratiques de réalisations de dessins géométriques : en clair, il n’y a qu’un minimum de référence à des propriétés géométriques.

Une présentation de Colette Laborde

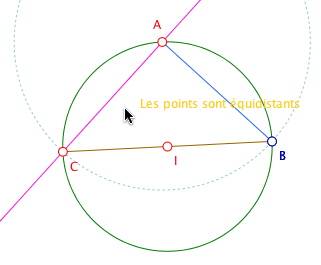
Lors du colloque TICE de l’IREM de Lille, de juin 2008, Colette Laborde - qui a beaucoup œuvré, par ses recherches en didactique, pour la reconnaissance institutionnelle de la géométrie dynamique (représentée alors par le logiciel historique Cabri Géomètre) - a proposé une activité pour entrer dans cette représentation de la figure comme devant résister au mouvement, dans un contexte scolaire de cycles 3. L’activité suivante n’est pas la première à effectuer par les élèves, on peut commencer par des activités d’appropriation de l’interface avec moins d’enjeu dynamique directement pris en charge par les élèves, comme on le verra au prochain onglet. Mais c’est une activité que l’on peut proposer pour introduire les règles de validation des figures géométriques.

On dispose d’une voiture, déplaçable par un point - ci dessous l’unique point gras - à laquelle il manque une roue. Il s’agit d’utiliser les outils à disposition (les palettes étant personnalisées) pour ajouter la roue manquante à la voiture.

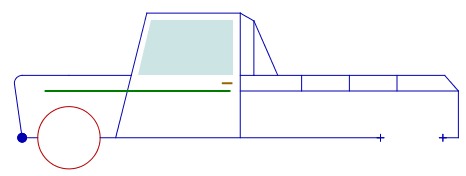
Une première démarche, appelée par Colette Laborde, l’activité du garagiste, consiste à prendre un cercle par centre et rayon fixe (a priori) et d’ajuster à vue le rayon à la roue, comme ceci :

Puis on valide en tirant sur l’avant de la voiture, qui suit, sauf la roue :

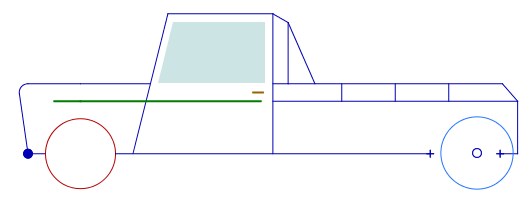
Ce comportement de la roue incite à accrocher la roue à la voiture, ce qui se fait facilement avec l’outil "cercle par centre et point. Les élèves parviennent, plus ou moins rapidement à cette situation :

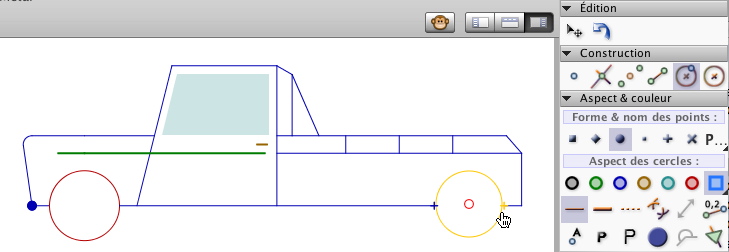
Nous reviendrons dans l’onglet suivant sur la difficulté d’utilisation de cet outil, mais ici la situation proposée par Colette Laborde est particulièrement bien conçue puisque, les élèves voulant accrocher la roue à la voiture, vont désigner naturellement un point de la voiture.

La validation par le déplacement produit alors quelque chose comme :

Ce qui commence à énerver passablement quelques élèves qui comprennent alors « qu’il faut aussi accrocher le milieu à la voiture ». Ces élèves là ont fait un premier pas vers la géométrie dynamique : ils ont compris qu’il fallait définir (« accrocher à la figure ») le milieu à partir de deux points de la voiture pour que la construction de ce point soit bien relative à la figure, intrinsèque, et donc associée à son mouvement.

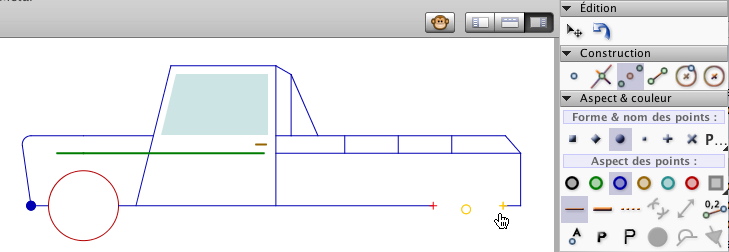
Bien entendu la compréhension est en acte, on reste encore dans une validation justifiée par l’action (en partie aussi parce que validée par le mouvement). Par ailleurs la validation est un simple mouvement de translation, avec une voiture invariante. Cette simplicité peut induire des représentations erronées.

Une représentation de l’aspect intrinsèque se fait lentement, au fil des activités, accompagnée par la mise en place d’un vocabulaire plus précis, spécifique au travail propre à la géométrie dynamique. Mais il est clair que la prise du milieu « pour accrocher la voiture » est un pas important vers l’appropriation des relations entre les objets et des propriétés associées, qui n’a aucun équivalent - en terme de validation - dans l’environnement papier crayon.

La voiture version « Formation des enseignants ».

C’est une figure (dans le classeur en ligne et téléchargeable en fin d’article) où il faut encore mettre la roue manquante. Régulièrement utilisée en formation, de nombreuses solution ont pu être testées, là encore avec parfois des « connaissances sociales implicites ». Un stagiaire a réussi a faire une construction correcte avec seulement 3 objets intermédiaires avant la roue finale.

On pourrait croire qu’il faut une bonne connaissance du logiciel pour faire cette roue en trois objets intermédiaires seulement. En fait, non, c’était bien au début d’une première séance sur le logiciel. Simplement le stagiaire a eu une idée originale. Son propos n’était pas du tout d’optimiser le nombre d’objets. La réactivité du logiciel - qui anticipe les construction d’objets pendant la manipulation - a fait le reste : elle permet d’apprendre sur le logiciel et d’optimiser en temps réel sa propre démarche.

C’est donc un exemple de l’efficacité du logiciel en terme d’outil d’auto-apprentissage ... et de celle des stagiaires qui savent être eux aussi très réactifs dans leurs propres apprentissages.

Des figures pour apprendre à cliquer correctement

Dans un premier temps les élèves transposent naturellement sur l’écran leurs représentations des dessins géométriques de l’environnement papier-crayon. Cela se traduit par l’utilisation des outils « au jugé », sans référence explicite aux relations en jeu entre les objets.

L’introduction de la géométrie dynamique en cycle 3 aura un sens si on parvient assez rapidement à installer ce changement de paradigme géométrique. C’est bien entendu à la charge de l’enseignant d’accompagner cette transformation. Le propos de cet onglet est d’installer un accompagnement préliminaire en acte, simplement opérationnel, sans véritable enjeu de conceptualisation. Cela peut se faire, sur la base d’un contrat d’apprentissage des icônes, par une instrumentation de l’outil logiciel, c’est-à-dire par son apprentissage de base.

L’objectif visé ici est tout à fait élémentaire : que les élèves prennent l’habitude de vérifier que le point qu’ils veulent sélectionner est bien surligné, et qu’ils apprennent qu’il l’est si on se rapproche du point sans être nécessairement sur lui avec le curseur de sélection.

On propose donc aux élèves des activités de tracés de segments pour apprendre à cliquer sur un point, si possible rapidement. Ensuite, on fera la même chose pour le cercle car il y a plus de problème dans le cas du cercle.

Puisqu’il s’agir d’installer - quand même - aussi cette première règle de géométrie dynamique : la validation de la figure se fait par la conservation de sa cohérence interne (ses relations ou ses propriétés) par le mouvement, il convient de proposer la même validation.

Voici donc quelques figures utilisables à cet effet (dans le classeur téléchargeable en fin d’article). Elle sont basées sur des tableaux de fils, puis des tableaux de cercles. Les élèves peuvent avoir des tableaux de fils différents.

Premier tableau : fils intérieurs à un rectangle.

Dans les trois figures suivantes, on travaille essentiellement sur des segments. Même si des explications sont rappelées sur la figure, plusieurs consignes peuvent être données oralement. Par exemple choisir des couleurs de segments par quadrant on par couples de quadrants.

En pratique on ne montre les noms des points que quand on en a besoin. Selon la classe, la pratique géométrique, on peut ou non s’en passer. Une fois le « dessin dynamique » terminé on cachera les points.

Deuxième tableau : fils sur le contour d’un rectangle.

Cette deuxième figure propose une activité peut-être plus simple. On peut rapidement ne plus avoir besoin des noms des points.

La validation permet de vérifier que l’on a bien cliqué sur tous les points. Voici une version qui mélange les deux, avant, puis après déplacement des points A et B.

Un retour papier crayon en CM2 donne par exemple ceci :

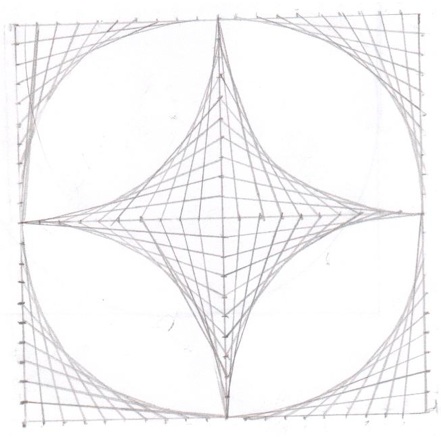
Troisième tableau : avec les diagonales d’un carré.

Il y a deux fois plus de segments, c’est donc plus long à faire. Là aussi il peut être intéressant de varier ou non les couleurs. On notera l’alternance des couleurs sur les diagonales pour mieux se repérer. Noter tout de même que selon la classe, le codage peut être superflu : il suffit de regarder le codage pour comprendre ce qu’il a à faire, et l’effacer pour effectuer la tâche.

Bien entendu de nombreuses autres variantes sont possibles, mais ce n’est qu’un exercice d’appropriation du surlignage jaune des objets sélectionnés : il n’y a pas d’enjeu mathématique, juste de l’instrumentation du logiciel.

Le tracé de cercles

En pratique il est souvent plus difficile pour les élèves de construire des cercles car il y a souvent ajustement du cercle au jugé, sans construire le cercle passant par un point. Cela vient naturellement de l’usage du compas dans l’environnement traditionnel. Le compas est d’abord un instrument de report de longueur : une fois l’ouverture donnée, on peut commencer le cercle où l’on veut. Les élèves transposent cela dans l’usage du compas logiciel : ils cliquent comme s’ils posaient le crayon quand l’ouverture du cercle leur semble - à vue - correcte. Mais le compas de la géométrie dynamique ne fonctionne pas comme cela : le rayon est donné par le second clic, et il faut un petit apprentissage pour s’approprier cet outil.

Par exemple pour le simple tracé de la rosace archétypique de l’école primaire, voici les gestes sur lesquels il convient d’être vigilant dés les premières utilisation du compas (la fiche élève « Du bon usage de la souris » rappelle ces consignes) :

Ce qu’il faut éviter : ci-dessus, à gauche le cercle est tracé à vu, comme sur un dessin, il n’est pas construit « passant par O ». L’élève va construire un nouveau point sans comprendre ce qu’il a fait (les « gestes fugaces » de l’analyse ERMEL) , ni pourquoi le cercle ne fait pas ce qu’il voulait : l’élève transpose son vécu « papier-crayon » à l’écran. À droite le surlignage de tous les cercles montre que le logiciel va prendre leur intersection et non pas le point O. Même si c’est un point superposé à O (au même endroit) cela complexifie grandement la figure, en particulier en terme d’interprétation.

Ce qu’il faut faire : ci-dessous, à gauche, on veut prendre l’intersection des deux cercle, donc on pose - avec l’outil point - le curseur sur l« intersection, les deux cercles sont surlignés, l’intersection est bien créée. À droite, c’est bien le point O qui est surligné, donc le cercle va bien être construit comme »passant par O".

Pour répéter ce geste tout en faisant une figure intéressante, voici un exercice de tracé qui correspond au limaçon de Pascal : sur un cercle donné, on se donne des points. On construit les cercles de centre ces points passant par un point fixe A. Voici la figure originale :

Les difficultés de l’utilisation sont résumées dans le montage suivant : on voit bien qu’il faut attendre le curseur de la main qui surligne le point que l’on veut prendre, sinon on prend l’intersection de deux cercles, ce qu’il faut éviter, même si, mathématiquement c’est le même point (l’élève construit alors beaucoup de points les uns sur les autres et ne comprend plus ce qu’il se passe ... ).

La figure est validée en déplaçant ou bien le point A (tous les cercles passent bien par A) ou bien le centre du cercle (tous les points du cercle ont bien été pris). En fait la figure proposée aux élèves est un peu plus sophistiquée, elle permet d’animer le point « 1 » (en rouge dans la vidéo suivante). Là encore c’est un mouvement qui valide que la figure est correcte. CaRMetal permet de continuer la figure pendant les animations, et ici en particulier, comme on le voit dans la vidéo, on peut déplacer le point A pendant que les cercles tournent

Vidéo du limaçon (8 s - 11 Mo)

Retour au papier-crayon

Ces quelques activités d’apprentissage du logiciel peuvent aussi être l’occasion de motiver à faire la même chose aux instruments usuels sur une feuille de papier, ne serait-ce que pour colorier les parties obtenues par intersection. Le travail des élèves est facilité en donnant un contexte préalable avec les points marqués. On trouvera en fin d’article des figures CaRMetal paramétrées (pour le nombre de points), ainsi que des versions imprimées prêtes à l’emploi. Le dernier onglet revient sur ce point en précisant les utilisations et quelques détails techniques.

Voici quelques exemples de travaux d’élèves, effectués - hors temps scolaire - dans le CM2 de Jean Daniel Nourby et la 6° de Virginie Morel, sur la cardioïde qui est le cas particulier du limaçon ci-dessus quand le point A est aussi sur le cercle de départ. Tout d’abord deux versions assez classiques :

et déjà motivantes

Et une version surprenante, d’une élève de 6° qui, en faisant ses cercles depuis le point A (comme quoi les procédures personnelles induisent souvent des visons personnelles), a su faire abstraction des intersections de cercles pour voir les cercles de rayon croissant au début, et a proposé ce coloriage :

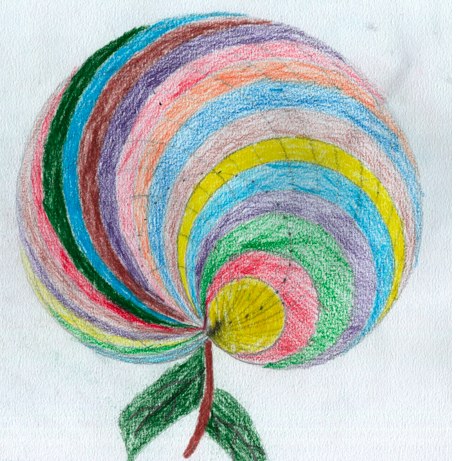
Le travail sur ordinateur, libérant des difficultés techniques, permet d’entrer plus facilement dans la compréhension d’une tâche de type algorithmique (ici répétition d’une tâche avec une modification à chaque étape), et, dans une logique d’expression plus artistique, peut ainsi motiver à revenir à un travail sur papier pour exprimer plus avant sa créativité. C’est la même chose avec les tableaux de fils, comme celui-ci :

où l’on voit bien qu’une certaine irrégularité dans l’application manuelle au départ ne perturbe pas l’esthétique générale produite.

Premières figures géométriques

Dans l’onglet précédent nous avions privilégié la manipulation de la souris, nous allons maintenant proposer des pas à pas élémentaires, mais indispensables pour réaliser ses premières figures géométriques et les premières investigations de propriétés géométriques.

L’idée est de donner quelques premières bases géométriques et quelques bonnes pratiques d’utilisation des outils, en particulier pour optimiser son choix d’outil.

Construction d’un rectangle

On reprend rapidement ce qui a été dit dans un onglet précédent en insistant cette fois sur la façon de cliquer sur les objets. Un rectangle est un quadrilatère qui a 4 angle droits. En pratique on en construit 3 et on vérifie que la quatrième est droit.

Autre définition envisageable ; un rectangle est aussi formé de deux paires de droites parallèles dont deux sont perpendiculaires. Cette dernière définition est plus conceptuelle mais elle a l’avantage de mettre en jeu des parallèles et de ne pas avoir à vérifier que le quatrième angle est droit. Dans cette définition on suppose connu que des droites sont parallèles quand elles ont une perpendiculaire commune.

Dans les deux cas, la construction est alors celle-ci :

Une pratique optimale pour réaliser cette figure peut être celle-ci :
– Prendre une droite (ou un segment), défini par deux points, A et B.
– Sélectionner l’outil « Perpendiculaire », et choisir (clic) le segment, puis le point A, le segment, puis le point B. On a un segment (ou une droite) et deux perpendiculaires à [AB] qui devient la perpendiculaire commune à ces deux droites.
– Toujours avec le même outil (sans le re-selectionner donc), choisir la deuxième perpendiculaire, et, en se rapprochant d’elle on choisit un point C : on a donc trois angles droits.
– Sans même avoir construit le quatrième point, commencer à construire les 4 côtés du rectangle, le point D est pris à la volée en s’approchant de l’intersection des deux droites qui doivent être toutes les deux surlignées pour le construire.
– On gomme les droites pour ne garder que les segments.

On notera que dans cette construction, on n’a pas utilisé d’autres points que ceux nécessaires à la figure, ainsi le rectangle est directement manipulable par A et B (qui peuvent se déplacer dans le plan), et C (qui peut se déplacer sur une droite). D’autres construction, avec les parallèles, selon comment elles sont pratiquées, introduiraient des points supplémentaires et donc une manipulation du rectangle obtenu à la fois plus complexe et moins directe (ce qui arrive souvent quand on laisse explorer les possibilités des outils pour faire un rectangle.

Construction d’un carré (à partir d’un côté).

– On commence de la même façon avec un segment [AB] et les deux perpendiculaires en A et B.
– Pour reporter la longueur AB sur la perpendiculaire, il suffit d’utiliser le cercle de centre B passant par A. Il coupe la perpendiculaire à [AB] en B en un point C.
– Note technique : plutôt que de choisir l’outil intersection qui ne sert vraiment que dans des cas plus complexes, on habituera les élèves à prendre le point C à la volée, c’est-à-dire avec l’outil point en se rapprochant de l’intersection, en cliquant quand le cercle et la droite sont surlignés en jaune.
– En fait on peut faire mieux, et, sans avoir construit C, sélectionner tout de suite l’outil « Perpendiculaire » et montrer une des deux droites déjà tracée (par exemple celle passant par A) et ensuite aller à l’intersection du point C : le logiciel construit C et la perpendiculaire passant par C.
– On termine comme pour le rectangle en nettoyant la figure avec le gomme et en construisant les côtés

Chacun est convaincu que ceci est une des constructions optimales d’un carré de côté donné. C’est l’occasion d’observer tous les implicites qu’il y a en géométrie car en pratique on a construit un quadrilatère ayant 3 angles droits et deux côtés consécutifs de même longueur. Ce n’est seulement qu’en 5° que l’on pourra argumenter sur de type d’optimisation. Avant, que cela soit suffisant est une propriété - outil - du carré. Néanmoins, la construction achevée, on peut vérifier avec les outils proposés que l’on a bien un carré. Nous allons le faire dans la deuxième partie de cet onglet.

Un quadrilatère à contraintes plus faibles

On peut proposer aux élèves de construire un quadrilatère ABCD ayant les côtés [AB] et [BC] de même longueur (même technique que le carré ci-dessus) et avec des angles droits en A et en C. L’intérêt est de proposer une figure qui a presque les mêmes prémisse du carré tout en étant bien différente. On l’utilisera aussi dans la deuxième partie de cet onglet. On obtient une figure de ce type (en ayant laissé le cercle de construction sur lequel est pris le point C).

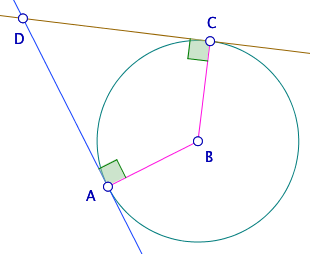
On appelle généralement ce quadrilatère un cerf-volant. Il a ses diagonales orthogonales sans se couper en leurs milieux. Ce cerf volant a aussi deux angles droits.

On peut aussi supprimer la contrainte « de même longueur » pour une figure encore plus générale : quadrilatère avec seulement deux angles droits.

Utilisation des outils de tests

On a déjà dit que la géométrie dynamique apporte un nouveau paradigme, en particulier en validant des relation ou des propriétés par l’invariance dans le mouvement, c’est-à-dire par validation d’une propriété sur de nombreuses instances de la figure.

Un autre changement de paradigme, peut-être cognitivement plus délicat que la manipulation directe des figures, est l’utilisation des outils de vérification des relations entre les objets. D’une part les outils sont radicalement différents. Pour reprendre les expressions d’ERMEL, ils sont « du côté de la théorie », du côté du géométrique. Pour tester un angle droit on n’utilise plus une équerre ou un gabarit du monde sensible, mais l’icône de test « Droites perpendiculaires ? ». Dans le monde sensible on valide à l’instrument une perception. La validation est, en définitive, elle aussi perceptive. Même si elle est objectivée par l’instrument, cette validation engage quand même la responsabilité de l’utilisateur, par sa manipulation de l’outil, par sa lecture de l’information produite par l’outil. Dans l’environnement numérique, si l’intuition est encore du côté perceptif pour la conjecture que l’on va vérifier, une fois cliqué sur les prémisse de l’outil de test, l’utilisateur n’a plus d’appréciation sur l’usage de l’instrument, le perceptif et l’utilisateur disparaissent dans l’évaluation de la relation étudiée et la production du résultat : on clique et le logiciel renvoie son test. L’évaluation n’est pas faite dans le monde sensible de l’écran, mais en interne, du côté de la géométrie.

C’est donc un changement radical qui fait entrer l’élève bien-sûr dans l’univers des propriétés géométrique, mais plus généralement dans un monde numérique (B2i) contemporain où de nombreux tests de validation sont effectués par des machines et n’auraient aucun sens à l’échelle humaine (test de validation des processus de micro ou nano technologie par exemple).

L’utilisation du test de parallélisme ou de perpendicularité ne pose pas de problème particulier. Les test d’alignement de trois points ou d’appartenance d’un point à une droite sont assez simples aussi même s’il convient d’être prudent si on veut jongler avec : cela nécessite une gymnastique conceptuelle non triviale pour les élèves de passer de l’un à l’autre, mais cela renforce bien entendu les représentations de l’alignement en terme d’appartenance. On peut, sur les exercices suivants, alterner un test d’alignement de trois points et l’appartenance de l’un des points à la droite passant par les deux autres.

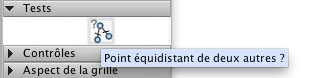
Par contre l’usage du test d’équidistance pour montrer que des longueurs sont égales n’est pas une simple instrumentation simple de cet outil, mais bien une instrumentalisation. Si on veut vérifier sur un quadrilatère que les côtés [AB] et [BC] sont de même longueur, on aurait pu, comme dans la construction de C, chercher à savoir si C appartient au cercle de centre A passant par B, mais cet outil n’existe pas (pas encore dans la version utilisée au moment de cette rédaction). On utilisera donc - ce qui est conceptuellement la même chose - que A est à même distance de B et C, en montrant les points A, puis B et C. Mais on comprend bien que pour les élèves on passe d’un discours sur les points à un discours sur les longueurs, même si « à même distance » n’est pas nécessairement du registre de la mesure.

Vérification du carré

Par construction les angles en A et B sont droits, les côtés [AB] et [BC] sont de même longueur. Selon la construction faite pour la troisième perpendiculaire, un des deux derniers angles est connu comme étant droit.

On peut vérifier ainsi que :
– Le quatrième angle est droit (et quel est ce quatrième angle à vérifier ?)
– Les côtés [BC] et [CD] sont de même longueur
– Les côtés [CD] et [DA] sont de même longueur
– Les côtés

DA et [AB] sont de même longueur

Propriétés des diagonales

On peut commencer par construire le milieu I de B et D et tester si I appartient [AC] en vérifiant si I est aligné avec A et C. On comprend bien que c’est une démarche volontairement conceptuelle. Selon la classe et la pratique géométrique on commencera par tracer les diagonales et vérifier l’appartenance de I à [AC], ce qui est plus facile à voir et à s’approprier. On peut ensuite tester si I est équidistant de A et C. Alors I est aussi le milieu de A et C.

On peut tracer les diagonales [AC] et [BD]. Et tester si elles sont orthogonales.

Malgré tous ces tests, ces propriétés pour les élèves relèvent de l’évidence puisque cela se voit sur la figure. On peut alors recommencer les mêmes tests sur le quadrilatère précédent, et commencer à prendre conscience qu’une propriété d’une figure n’est pas une évidence en soi, qu’elle peut particulariser une figure (parfois la caractériser), d’autant que sur cette figure, on peut déplacer C pour que le milieu de [BD] vienne sur [AC] et alors ABCD devient - visuellement - un carré :

« visuellement » car en manipulation directe on n’arrivera jamais à l’angle droit « exact » pour le logiciel. Il ne faut pas tester la propriété sur l’illustration de droite, les tests logiciels sont trop précis.

Droites concourantes par appartenance d’un point à une droite

Là encore il s’agit d’instrumentaliser un outil pour l’utiliser à autre chose que ce qu’il est prévu de faire. Ce paragraphe est proposé à titre informatif, il est conceptuellement trop délicat pour le proposer à des élèves de l’école primaire, mais serait réalisable en collège.

On se propose de travailler avec l’orthocentre d’un triangle pour observer une propriété, la conjecturer, et chercher une façon de valider la conjecture avec les outils de test que nous avons à notre disposition.

À partir d’un triangle ABC on construit les trois hauteurs (les perpendiculaires à un côté passant par le troisième sommet du triangle). On peut s’apercevoir, en déplaçant les points A, B, ou C d’un invariant frappant : les trois hauteurs semblent passer par un même point. Comment valider cette conjecture ? On peut prendre l’intersection de deux hauteurs (pour ne pas se tromper, exceptionnellement avec l’outil intersection et bien montrer cette fois les deux droites et pas l’intersection car il y a trois droites). On peut prendre les hauteurs issues de A et B. Notons H ce point, il appartient donc à deux hauteurs.

Alors les trois droites passent par un même point - et ce sera H - si H appartient à la troisième hauteur, celle issue de C, ce que l’on peut valider avec le test d’appartenance. Chacun comprendra que ce passage (concours

de présentation des outils du logiciel quand il s’agissait d’utiliser les tests dans le logiciel pour confirmer les propriétés à construire.

Cet onglet propose des activités de reproduction de figures, dans un registre géométrique (ie non numérique) pour faire fonctionner le vocabulaire et les relation entre les objets. L’investigation porte essentiellement sur la prise d’information pour rendre compte de la figure à produire en terme de propriétés géométrique.

Nous avons fait le choix d’utiliser des exercices de la collection CAP Maths, directement associée aux productions de ERMEL. Mais chacun peut adapter ce travail général d’investigation à d’autres figures.

Exemple 1 : activité sur les cercles de rayon fixe

Ce premier exemple semble en contradiction avec ce qui précède car il va utiliser les mesures. En ce sens il est à prendre comme un exercice de transition vers une re-géométrisation des activités géométriques. Techniquement, pour l’élève, c’est l’occasion d’utiliser en situation de construction l’outil « cercle de rayon fixe ». Pour l’enseignant, cet exercice est aussi un prétexte pour illustrer les possibilités d’investissement des propriétés des objets en réinterprétant les relations métriques.

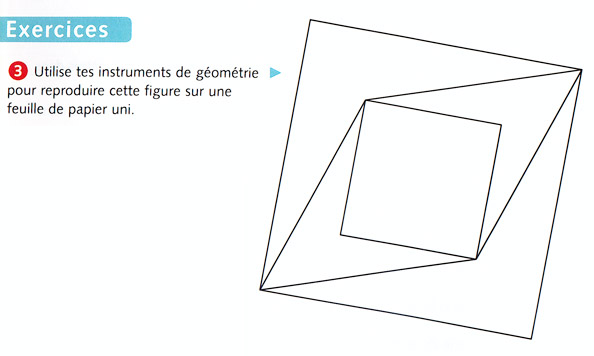
L’exercice est tiré du fichier élève de CAP Maths CM1, il s’agit de reproduire cette figure :

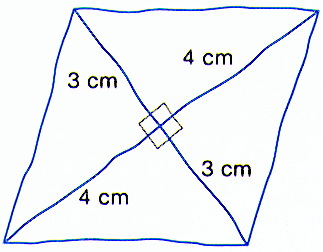
Dans l’environnement papier-crayon, on commence par construire deux droites orthogonales. Ensuite l’élève peut mesurer 3 cm directement sur la figure à partir du point d’intersection - on est alors dans la construction d’un point d’une droite à une distance donnée d’un point fixe. L’élève peut aussi prendre un écart de 3 cm au compas, à partir de sa règle - on est alors dans le report d’une longueur au compas. Dans un cas la situation se place principalement dans un registre numérique, dans l’autre dans un registre géométrique, la mesure étant alors comme un gabarit, dont on veut vérifier la qualité de la mise en œuvre.

Dans l’environnent numérique, tout d’abord la disponibilité des outils est une variable didactique importante, d’autant qu’elle induit les pratiques et les réflexions des élèves.
Dans ce cas là, l’élève voit qu’il ne dispose que d’un type de cercle, celui dont on peut donner le rayon.

Une organisation de l’activité peut commencer par une réflexion sur l’interprétation du dessin en terme de propriétés de la figure : il s’agit de construire un quadrilatère dont on connait des contraintes sur les diagonales. Le point d’intersection des droites orthogonales (notons le O pour la suite) est à 3 cm des deux sommets sur une des diagonales et à 4 cm des deux autres sommets sur l’autre diagonale.

Après cette première phase de une mise en mots géométriques du dessin proposé, on aborde, dans une deuxième phase, l’interprétation de ces données en relations géométriques. En terme de cercle, on cherche à ce que la petite diagonale soit réinterprétée comme le diamètre d’un cercle de centre O et de rayon 6, les sommets étant alors les deux points d’intersection de la diagonale et de ce cercle.

Nous avons volontairement conservé un vocabulaire un peu flou (comme celui des élèves), car la difficulté est d’interpréter le mot « diagonale » une fois comme un segment, une diagonale du quadrilatère, et une fois comme l’une des deux droites initiales perpendiculaires entre elles. En pratique on parlera de l’intersection de la droite et du cercle pour obtenir les sommets du quadrilatère sur une diagonale.

Selon la classe (CM1 ou CM2), la place de cette activité dans la progression géométrique et l’usage préalable du logiciel, on peut ensuite soit guider la construction - en structurant en étapes - soit laisser les élèves chercher eux mêmes (on aura rappelé la construction d’un cercle de rayon 3).

D’expérience, si on laisse les élèves construire d’abord les deux cercles avant de construire les 4 points, c’est assurément intéressant, mais réservé à des élèves qui savent - comme il est dit dans les instructions officielles - « extraire une figure simple d’une figure complexe », c’est-à-dire ici savoir placer correctement les points. En général il est préférable de préparer, sur fiche, des étapes : d’abord un cercle, les deux sommets, un autre cercle, les deux autres sommets.

Finaliser la figure

Pour construire le quadrilatère final, il peut être vraiment intéressant de tracer les segments avec la mesure affichée. On arrive alors à ceci :

On obtient un quadrilatère dont les quatre côtés sont de même longueur, les élèves peuvent connaître son nom. La propriété mise en évidence peut être abordée pour faire fonctionner le vocabulaire, mais ce n’est pas un exigible du cycle 3 (seulement au programme de 5°) : diagonales orthogonales, se coupant en leurs milieux.

Par contre, si on a fait afficher la mesure des côtés du losange, il faut aller un peu plus loin. En effet, trouver 5 comme mesure, sans autre précaution, peut inférer une règle 3 - 4 - 5 comme « trois nombres consécutifs ». Aussi on proposera une dernière activité, à savoir remplacer le cercle de rayon 3 par un cercle de rayon 5 : les cercles initiaux sont 4 et 5. On obtient bien une longueur identique pour tous les côtés du quadrilatère, mais pas 6.

Le zoom à la molette

On notera que le zoom dans CaRMetal se fait à la molette. Mais il n’y a pas de modification des longueurs, c’est seulement l’échelle qui est modifiée (autrement dit c’est un vrai zoom). Cela permet d’aller loin dans la précision, par exemple pour le lycée. On peut zoomer jusqu’à 400 fois.

Exemple 2 : propriétés sur les carrés

Dans ce deuxième exemple, extrait du CAPMaths CM2, nous abordons réellement les relations géométriques de la figure et les outils de la géométrie dynamique pour explorer les figures. L’activité d’investigation va consister à dépasser l’évidence perceptive pour décrire la figure à reproduire en terme de relations et de propriétés. Cette description amenant ensuite naturellement à un programme de construction

Dans l’environnement papier-crayon, on peut mesurer les longueurs des côtés, et vérifier à l’équerre les angles droits. On constate alors, aux imprécisions de mesure prés, que carré extérieur à ses côtés de longueur double par rapport à ceux du carré intérieur. Mais ce n’est pas essentiel pour la construction, le plus important étant les positions des sommets. Plus encore sur les diagonales, les mesures sont arrondies pour valider les positions. On voit bien les nombreux implicites (nécessaires) pour s’entendre sur un rapport de longueur entre les diagonales : on comprend qu’il est de 2 même si les mesures ne donnent pas tout à fait ce rapport là. Le même résultat peut être obtenu aussi au compas, sans mesurer les longueurs, en ayant mis en évidence le centre du carré intérieur par l’intersection des diagonales. Dans ce cas, seule la précision de la manipulation du compas est en jeu, et là aussi les imprécisions amèneront à faire l’hypothèse d’un rapport 2.

La construction dans l’environnement papier-crayon est moins guidée que dans dans une figure dynamique. Pourtant, de fait, tous les élèves partent pratiquement toujours du carré extérieur. La construction est longue, mais elle participe aussi de l’apprentissage de la manipulation des outils de constructions géométriques.

Les enjeux d’une transcription numérique de l’exercice

La version numérique est différente. Et le travail d’investigation pour valider la figure à reproduire va l’être aussi.

On se donne donc une figure (les quadrilatères ABCD, MNPQ et ANCQ) ainsi qu’un segment [AB], en marron - qui représente un premier trait tracé par report au compas - à partir duquel on demande de reproduire la figure.

Il y a de nombreuses différences avec l’environnement papier-crayon. Tout d’abord on peut modifier la figure par les points O et A (mais aussi les points marrons A et B). La figure reste « pareil » comme disent les élèves, mathématiquement on dirait « semblable » : la figure se translate par O et change de taille et d’orientation en déplaçant A. Cela permet d’installer plus concrètement que l’on ne s’intéresse pas au dessin mais bien à la figure, c’est-à-dire aux relations entre les éléments qui la composent. Ensuite cela permet de placer les quadrilatères dans toutes sortes de configurations (instances) sans direction privilégiée. On notera aussi qu’il n’y a pas de mesure, et on se propose de reproduire la figure dans un registre uniquement géométrique.

Une deuxième différence est dans l’implicite de séquentialité de construction : le fait que les figures dynamiques ont des points « de base », privilégiés pour la manipulation des figures, donne des indications précieuses pour commencer la construction de la figure, indications qui n’existent pas dans l’environnement papier crayon. C’est la raison pour laquelle on a proposé dans cet exercice, les points A et B pour reproduire la figure : on reprend bien l’idée que l’on va travailler d’abord sur le quadrilatère extérieur, mais on impose aussi une modification de ses propres éléments de base, le côté au lieu du centre et d’un point.

La troisième différence, plus cognitive que les deux précédente, est l’utilisation des outils de vérification des relations entre les objets. Nous l’avons déjà analysée à l’onglet « Premières figures ».

Détermination des propriétés d’une figure

Il s’agit d’une version faible de ce que l’on appelle l’investigation en général, alors que l’exercice proposé dans l’onglet « Problème ouvert » était plus large sur ce point puisqu’il validait, par une argumentation, ce que l’on avait recherché.

Dans cet exercice, on demande aux élèves de mettre en œuvre les relations entre les objets pour vérifier les propriétés qui définissent les figures intermédiaires. Ainsi, dans un premier temps on demande aux élèves de vérifier que ABCD est bien le quadrilatère qu’ils imaginent (un carré), et d’en rendre compte sur fiche. Puis on analysera les positions des points pour envisager la construction.

Vérification de la nature de ABCD. On veut justifier que c’est un carré. Il faut d’abord vérifier les 4 angles droits (instrumentation immédiate). C’est alors déjà un rectangle. Ensuite que les 4 côtés sont de même longueur (1). On a déjà mentionné (onglet « Premières figures ») que l’outil utilisé demande à être instrumentalisé : il faut apprendre à utiliser l’outil « équidistant », plus orienté sur les points : [AB] et [AD] ont même longueur si A est équidistant de B et D. En cliquant sur cet outil, il faut montrer d’abord le sommet A et ensuite les deux points dont on test l’équidistance à A.

Vérification de la nature de MNPQ : même démarche si on le souhaite, mais cela peut aussi ne pas être fait car on peut construire MNPQ sans utiliser sa nature, avec les tests suivants.

Alignement des points A, M, O, P, C. On se souvient que le test d’alignement vérifie l’alignement de 3 points. On fera les alignement que l’on a besoin, mais cela fait beaucoup car il n’est pas question de faire des raisonnement logiques sur les implications d’alignement. En pratique, il est plus simple de construire la droite (AC) et de vérifier, avec le test d’appartenance, que les autres points sont bien sur cette droite. Dans cette situation, une réflexion sur l’appartenance d’un point à une droite est bien plus économique qu’une autre sur de nombreux alignement. La difficulté conceptuelle - effective chez beaucoup d’élèves - pour passer de l’un à l’autre est ici uniquement dans le choix d’une droite. Dans la fiche de travail on peut choisir de guider les élèves en proposant de construire une droite précise, ou simplement de construire une droite à partir de deux de ces points, on aura alors des productions différentes.

Relation entre A, M et O. On a déjà plusieurs fois utilisé, dans cette activité, le test d’équidistance pour rendre comptes de longueurs égales, mais ce n’était pas dans un contexte de points alignés. Il est possible que les élèves ne transposent pas la propriété sur des points alignés, sauf éventuellement si on a traité auparavant les exercices associés sur le carré à l’onglet « Premières figures ». Ayant constaté l’alignement des trois points A, M, O, et maintenant les longueurs égales, on en déduit que M est le milieu de A et O. On fera de même pour la position des autres sommets du carré intérieur. Il est clair que l’utilisation des tests du logiciel place l’activité beaucoup plus du côté des relations géométriques que la même activité dans l’environnement papier-crayon, où, à force de mesures, on finit par entrer dans la logique d’une reproduction de dessin.

La construction de la figure. Les recherches précédentes des relations entre les objets et les activités préalables peuvent maintenant être assemblées pour construire d’abord le carré ABCD (comme fait précédemment dans l’onglet « Premières figures ») puis en prenant les quatre milieux, MNPQ et en terminant par le troisième quadrilatère dont on pourrait observer que c’est un losange.

Variante de cet exercice

Sur la même double page, le fichier CAPMaths propose cet autre exercice qui n’est qu’une variante de celui-ci, les points utilisés étant les mêmes, seuls l’agencement des segments changent.

On pourrai proposer une variante de celle-ci, si on souhaite que les élèves n’aient pas les mêmes figures à faire, ou que l’investigation soit (légèrement) différente. Par exemple, au lieu de mettre les sommets du carré extérieur à une distance double du centre, on peut les mettre à la distance de la longueur du carré intérieur. Voici sur une figure les deux constructions possible, à partir du carré intérieur cette fois. En vert, la figure comme proposée dans CAPMaths, en rose, la variante en prenant comme distance la longueur AB comme en atteste l’utilisation du cercle.

Dans les deux cas, on procède avec un cercle puisqu’il s’agit cette fois de construire le grand carré à partir du petit. Dans le cas de la figure du fichier CAPMaths, on prendrait le cercle de centre A passant par O pour faire - avant l’heure - le symétrique d’un point, mas en réinvestissant le vocabulaire et les propriétés de base du cercle, ici rayon et diamètre : on a a construire un diamètre connaissant un rayon. Le cas de la nouvelle variante est peut-être « plus simple » au sens où les points n’étant pas alignés on est plus naturellement dans une démarche de report de longueur.

Exemple 3 - construction sur un cercle

Voici un dernier exemple, toujours tiré du fichier CAPMaths CM2, qui présente un nouvel intérêt.

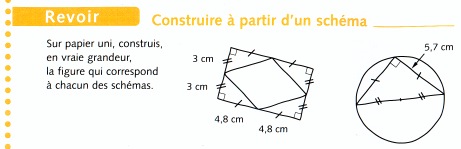
Nous ne ferons que la figure avec le cercle, sans préciser de mesure au segment donné comme initial. Une première analyse de la figure peut être proposée, avant la réalisation. On peut s’attendre à ce qu’un point soit délicat - si du moins les élèves commencent à anticiper sur les constructions géométriques, car une fois construit le triangle et le milieu I du côté [BC] opposé à l’angle droit A, il n’y a aucune raison a priori, pour que le cercle de centre I passant par B ou C passe aussi par le sommet. Les élèves les plus dans l’anticipation peuvent être gênés par cette contrainte supplémentaire, et même penser qu’elle est liée à la longueur 5,7 cm.

Dans cette activité, une fois la figure terminée, on invite les élèves à observer une propriété non attendue : le cercle de centre I passant par B semble aussi passer par A. On proposera alors de valider la propriété observée par un test : par exemple que I est équidistant de C que de A et interpréter ce résultat en terme de rayon du cercle.

Notes de l’onglet

(1) C’est la définition usuelle. Mais les élèves peuvent savoir - selon la classe et la pratique géométrique que c’est un rectangle avec deux côtés consécutifs de même longueur, dans ce cas il n’y qu’un test à faire.

Conclusion de cet onglet

L’activité de « programme de construction » est difficile à mettre en œuvre au cycle 3, dans l’environnement papier-crayon, pour plusieurs raisons dont la difficulté à repérer puis exprimer les tâches à effectuer en terme de relations géométriques, et l’organisation séquentielle de ces tâches.
La pratique de la géométrie dynamique, sur des activités de reproduction de figure, parce qu’elle s’affranchit de la dimension sensible des outils dans l’évaluation des relations, permet d’introduire une démarche d’analyse géométrique systématique des figures avant leur reproduction.

La construction de la figure par l’élève juste après cette analyse, sur la même figure, évite le recours - mathématiquement lourd en cycle 3 - à l’écriture d’un programme de construction tout en ayant cette dimension d’analyse et de production croisée : l’activité de communication que l’on a pu faire dans l’environnement papier/crayon se retrouve partiellement dans le rapport que l’élève entretien avec les réponses produites par le logiciel aux tests qu’il lance. C’est l’effet miroir largement analysé des E.I.A.H (environnements informatiques d’apprentissages humains) appliqué à l’apprentissage des relations géométriques.

Enfin, une continuité de ces activités de reproductions de figure au sein d’un logiciel de GD est assez naturellement la reproduction des figures dans l’environnement papier crayon, par exemple dans les moments d’autonomie en classe. La phase d’exploration et de description géométrique étant déjà faite, une première réalisation effectuée de manière numérique, la tâche aux instruments physiques est alors plus centrée sur la précision de leur utilisation pour les tracés.

Compléments techniques pour une utilisation en « papier-crayon »

Outre l’intérêt intrinsèque de l’utilisation de la géométrie dynamique en classe pour une meilleure appropriation des concepts géométriques, la facilité à reproduire - en les comprenant - des figures simples et esthétique peut motiver à faire ces figures esthétiques « soi-même », c’est-à-dire dans l’environnement habituel, celui où il y a une trace physique de sa production.

Pour cela, les élèves peuvent être aidés en leur fournissant des grilles de travail pré-établies, l’objectif mathématique étant de favoriser l’usage des instruments physiques pour un travail soigné, hors temps scolaire bien entendu.

Dans cet onglet nous proposons différentes trames, largement paramétrées, et nous expliquons comment s’en servir. Ces trames sont construites par programmation dans un langage interne au logiciel qu’il n’est pas du tout nécessaire de connaitre pour les utiliser. Les fichiers fournis sont : le classeur des 6 trames, directement utilisable, le classeur des 6 figures, avec les scripts non lancés pour les enseignants du secondaire qui peuvent être intéressés par les scripts, et des dossiers zippés de quelques productions directement utilisables.

Le principe général d’utilisation

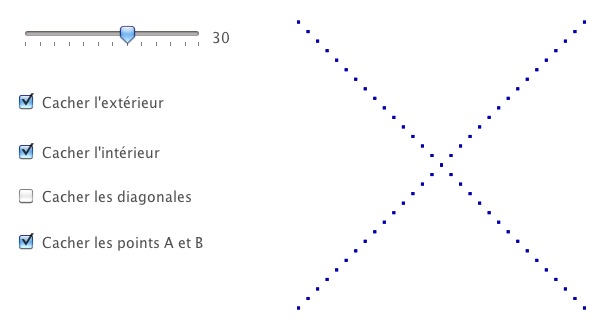
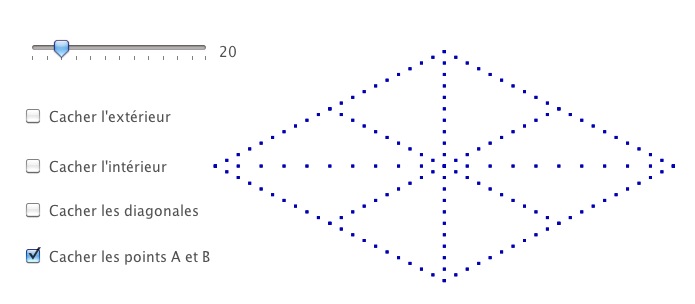
Il y a trois figures de base, carré, hexagone, pentagone. Chaque figure est produite en deux exemplaires, avec des points fins ou avec des points en gras. Les points en gras peuvent servir pour des brouillons, des élèves ayant des difficultés à voir les points ou pour des impressions sur imprimante A3.

Chaque figure dispose d’un curseur pour déterminer le nombre de points par segment, et de plusieurs cases à cocher pour afficher ou non certaines parties. Les copies d’écran suivantes sont nécessairement réduites, et peuvent faire illusion sur la taille des points car l’utilisation est prévue pour une dimension bien plus grande (voir plus bas) simplement en zoomant sur la figure.

Trois exemples de la trame carrée

Le nombre de points par segment va de 12 à 40 et il est toujours pair. Comme il y a trois cases à cocher, il y a 8 variantes de cette figure. En voici une seconde, dans le mode « Gras »

qui correspond à la dernière figure élève montrée dans l’onglet "Premières Manipulations. Quelques élèves ont besoin d’indicer à nouveau les points :

Puisque l’on peut déplacer les points A et M, on peut aussi modifier la forme du motif général, par exemple comme ceci :

Deux exemples de la trame hexagonale

Le principe est le même mais le nombre de variantes bien plus élevé. En voici une :

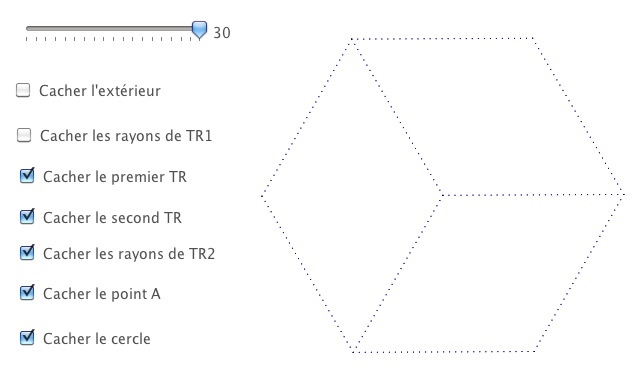
S’il y a 32 variantes possibles, toutes ne sont pas pertinentes, seules 16 sont intéressantes (ce qui est déjà beaucoup).

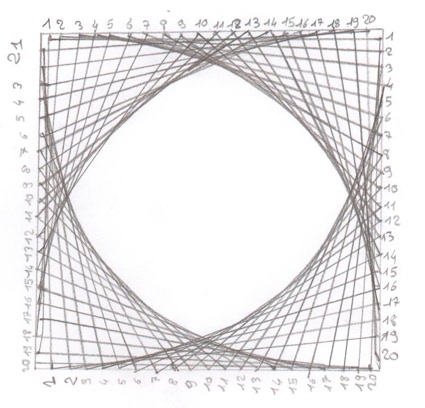
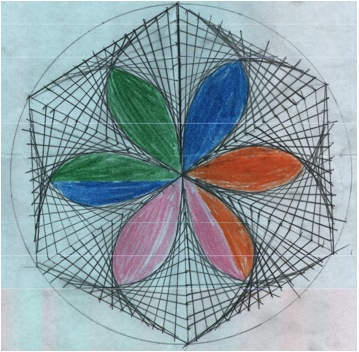
Rappelons que l’objectif est de faire travailler l’usage précis des instruments, ici la règle, et de laisser les élèves exprimer une créativité géométrique par un coloriage particulier. voici deux productions d’élèves (CM2 et 6°) :

Puisque les figures sont disponibles, y compris en ligne, même si ce n’est pas du tout l’objectif, parfois les élèves font la figure dans le logiciel et la colorie ensuite, c’est le cas avec un élève de 6° :

Un exemple de la trame pentagonale

Malgré les choix des options, en pratique, le nombre de sommet impair ne permet pas vraiment beaucoup de variantes significatives comme l’hexagone.

Mais on peut faire des choses assez jolies comme cette figure (sur logiciel ici)

Avec les cercles

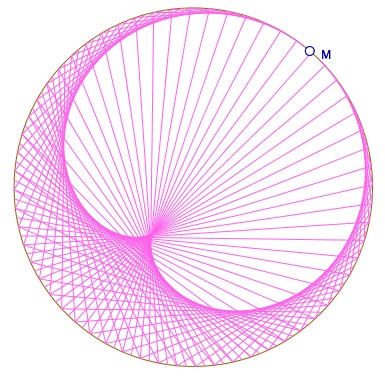
Nous avons déjà parlé du limaçon de Pascal et de la Cardioïde par le tracé de cercles. Pour cette dernière le point A de l’illustration ci-dessous est seulement un des points du cercle choisi par l’élève.

Mais la cardioïde peut aussi s’obtenir par l’enveloppe de segments. C’est en particulier la raison du numérotage possible des points dans la figure proposée (pour une première approche avec le logiciel) :

car il faut faire deux tours et relier le point n au point 2n. Deux versions sont disponibles, en ne nommant qu’un tour, et les élèves doivent trouver tout seul un algorithme de type local : « quand (l’indice de) l’extrémité d’un segment augment de 1, l’autre extrémité augmente de 2 ». On arrive à des productions papiers qui peuvent ressembler à ceci (ici en version dynamique, on peut déplacer la cardioïde par M).

Mais comme on l’a vu ci-dessus avec l’exemple du carré, pour un exercice comme celui-ci les élèves ont besoin de numéroter les points. Aussi une version spécifique permet d’avoir les indices sur les deux tours. Il n’y a plus de calcul à faire mais l’objectif est bien de percevoir l’algorithme précédent avant de passer à la production papier. La figure ressemble alors à celle-ci :

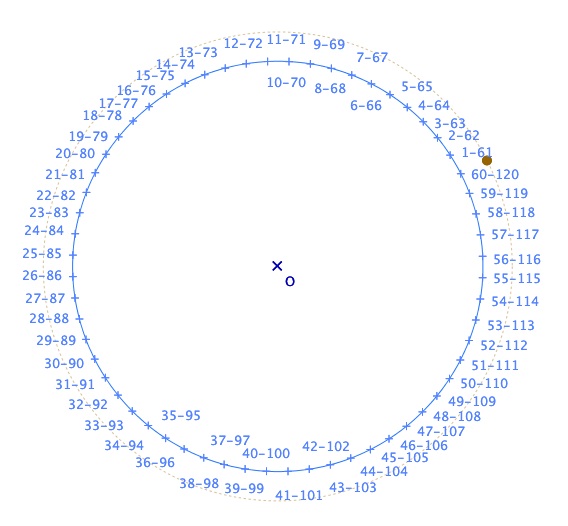
Et l’on voit bien qu’il est préférable d’apprendre un algorithme plutôt que d’utiliser un document aussi difficile à lire. Chacun remarquera d’ailleurs que ce type de document , peut aussi être l’occasion d’un travail de réinvestissement arithmétique.

L’utilisation des figures pour produire des documents papier

Pour une sortie A4, on peut utiliser les figures à points normaux. Pour une sortie A3 on utilisera les figures à points en gras (par exemple pour faire des affiches d’exposition). Si on dispose d’un grand écran on peut agrandir au zoom la figure. Ensuite faire une exportation PNG. Celle-ci ne prend que la figure, il n’y a ni le curseur ni les boites à cocher. Mais surtout, en PNG, on peut agrandir trois fois les dimensions de la figure

Ce qui permet des sorties tout à fait satisfaisantes pour une utilisation par des élèves.

En fin d’article on peut télécharger toutes les figures. Si quelques exemples de copies d’écran agrandies sont immédiatement utilisables, il reste préférable de télécharger le logiciel et d’utiliser les figures pour faire ses propres choix dans les options et le nombre de points.