Pour composer l’urne décrite par Condorcet ci-dessus, on commence par créer un sac vide (en fait, une liste vide transformée en sac) puis on y ajoute 90 fois de suite une boule blanche, et 10 fois de suite une boule noire :

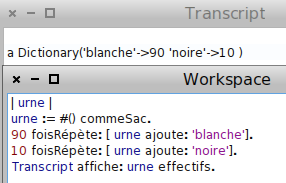
Ensuite, une main innocente est modélisée par auHasard ; ici sollicitée 8 fois :

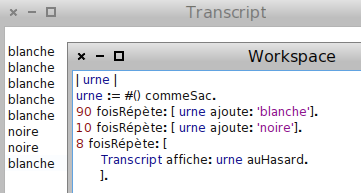
Pour répéter 1000 fois le tirage (avec remise) d’une boule dans l’urne, le plus simple est de créer un autre sac initialement vide et d’y stocker, au fur et à mesure, les résultats des tirages ; après ça on peut faire des statistiques sur ce sac, par exemple afficher ses effectifs :

Cette simulation de tirages avec remises permet de découvrir expérimentalement les variables binomiales : Par exemple, le nombre de boules blanches dans l’expérience avec 8 répétitions ci-dessus suit une loi binomiale de paramètres 8 et 0,9.

On peut enrichir l’exemple des billets de Laplace, avec des billets sur lesquels quelque chose est imprimé : Des cartes à jouer. Pour construire un jeu de 32 cartes, on choisit une liste de valeurs (as, 7, 8, 9, 10 et les figures) et une liste de couleurs (carreau etc.). Puis on boucle sur les valeurs, et sur les couleurs, en concaténant (par une virgule en MathsOntologie) la valeur, le mot « de », puis la couleur, et en ajoutant la carte ainsi construite dans le jeu de cartes (un sac évidemment) :

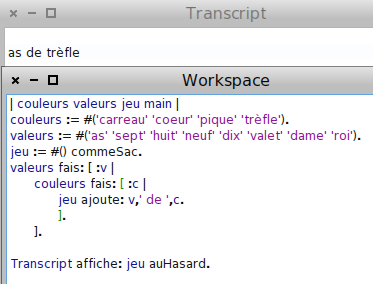
Pour simuler une main au poker, on pense à répéter 5 fois le tirage d’une carte :

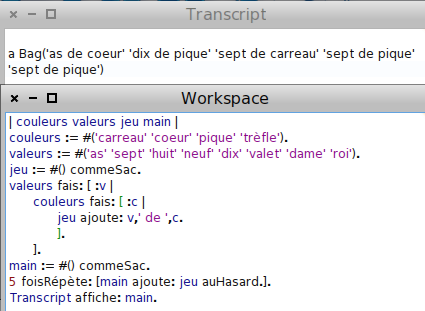
Las ! Le 7 de pique est sorti deux fois dans l’exemple ci-dessus. Cela est dû à ce que le tirage est fait avec remise, ce qui permet d’avoir deux fois (voire plus même si c’est rare) la même carte. En stockant ladite carte dans une variable carte avant de la placer dans la main (encore un sac !) on ne résout certes pas le problème :

(c’est le valet de pique qui est sorti deux fois).

Cependant, il suffit d’enlever cette carte (plus précisément toutes les cartes qui lui sont égales) du jeu pour avoir un tirage sans remise, comme le prouve le nombre de cartes restantes dans le jeu :

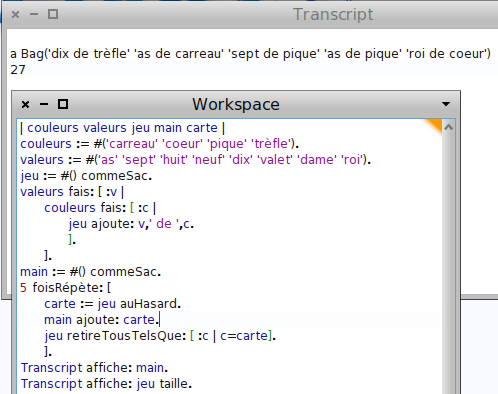
Les tirages sans remises permettent de constituer des échantillons, sur lesquels des activités intéressantes peuvent être menées en classe.

Poker à 52 cartes

Le modèle d’Ehrenfest complète les tirages sans remises : Non seulement on ne remet pas la boule dans l’urne, mais on la met dans une autre urne. Il faut donc

• numéroter les boules pour savoir dans quelle urne se trouve la boule choisie ;
• avoir deux urnes : L’une initialement pleine, l’autre initialement vide ;
• choisir une boule au hasard, et stocker son numéro dans une variable éponyme ;
• Si cette boule est dans l’urne 1, l’en enlever, et la placer dans l’urne 2 ; sinon faire le contraire :

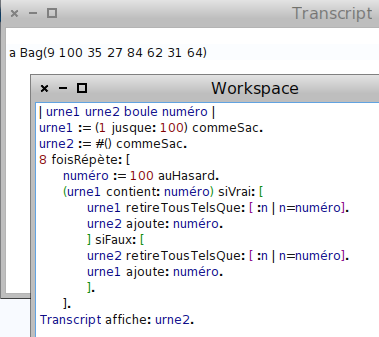
Évidemment, il est rare après 8 répétitions que l’urne 2 contienne moins de 8 boules, parce que la probabilité de tirer une boule d’une urne presque vide, est très faible. Après 100 tirages, la situation est différente :

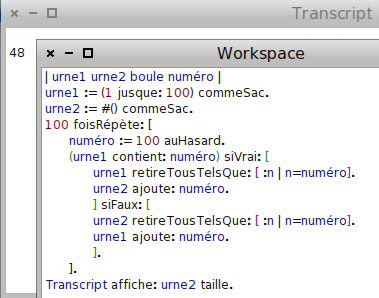
Ci-dessus, il ne reste plus que 48 boules dans l’urne 2, parce que plusieurs d’entre elles sont retournées à l’urne 1.

On peut étudier l’évolution du nombre de boules de l’urne 2 par un procédé similaire à celui du premier onglet :

• créer une « collection ordonnée » initialement vide (avec stats := #() commecollectionOrdonnée)
• à chaque répétition, y stocker le nombre de boules dans l’urne 2 (avec stats ajoute: (urne2 taille))
• observer le résultat après un millier de prélèvements (notamment, son écart-type).

version MathsOntologie

L’urne de Polya quant à elle, enrichit la notion de tirage avec remise : Non seulement on remet la boule dans l’urne, mais on en ajoute une de même couleur. Pour mettre un peu de gaité, plutôt que les boules blanches et noires de Condorcet, on prend des boules rouges et bleues ; et on s’intéresse à l’évolution de la proportion de boules rouges. Il suffit pour cela, de rajouter au sac, un duplicata de la boule qu’on vient de tirer :

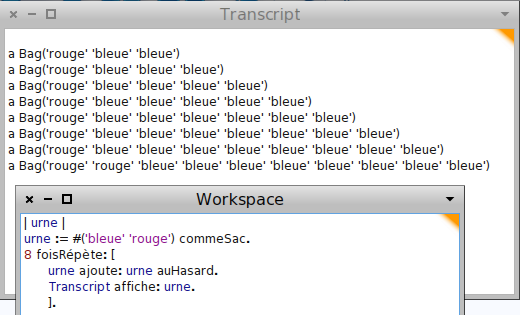
On constate une stabilité (nombre de boules bleus croissant) dans l’instabilité (du fait qu’il y a beaucoup de boules bleues, il y a peu de chance de tirer une boule rouge, et donc de modifier leur nombre). Comme on s’en doute, l’inverse peut aussi arriver, et d’autres situations intermédiaires :

Les proportions de boules rouges semblent équiprobables, comme on le vérifie en recommençant 100 fois une expérience de Polya à 9 boules :

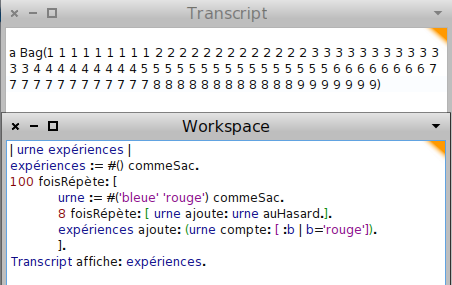
Même avec 1000 répétitions, le tableau des effectifs montre que les répartitions sont équiprobables sur l’ensemble des nombres de 1 à 9 :

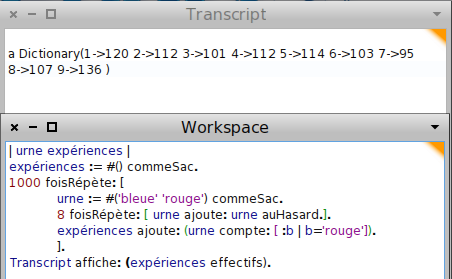
Les diagrammes en bâtons le confirment visuellement :

avec 81 boules

Le tableau des effectifs est peu utile à cause de sa longueur :

Aussi un regroupement par classes est-il préférable :

Lui aussi montre une équiprobabilité.

Ce micromonde n’est pas nécessaire pour étudier ce modèle, un algorithme numérique suffisant :

1. En appelant r le nombre de boules rouges et b le nombre de boules bleues, on initialise r et b à 1 ;
2. Dans une boucle,
   1. on commence par calculer un nombre pseudoaléatoire entre 0 et 1 (« random ») ;
   2. S’il est plus petit que r/(r+b) on incrémente r ;
   3. sinon on incrémente b
3. on affiche la nouvelle valeur de a/(a+b).

Mais c’est quand moins intuitif que le modèle avec le sac.

Urne de Polya

Expérience

Comment ça marche

Au départ, l'urne contient deux boules, une bleue et une rouge. À chaque répétition, on extrait au hasard une boule de l'urne, et on rajoute dans l'urne une boule de même couleur.

Tout recommencer

Tirer une nouvelle boule

L'urne contient 1 boules rouges et 1 boules bleues; soit un total de 2 boules actuellement.

Sur le long terme

À la longue, la proportion de boules rouges se stabilise mais sur quelle valeur ?

Replacer 380 fois une boule

En recommençant plusieurs fois l'expérience, on constate qu'à peu près toutes les répartitions entre 0 et 100% sont atteintes asymptotiquement:

Statistiques sur 8 répétitions

On répète 1000 fois l'expérience de répéter 8 ajouts de boules:

Répéter 1000 fois l'expérience

Statistiques sur 50 répétitions

On répète 1000 fois l'expérience de répéter 50 fois l'ajout de boules:

Répéter 1000 fois l'expérience

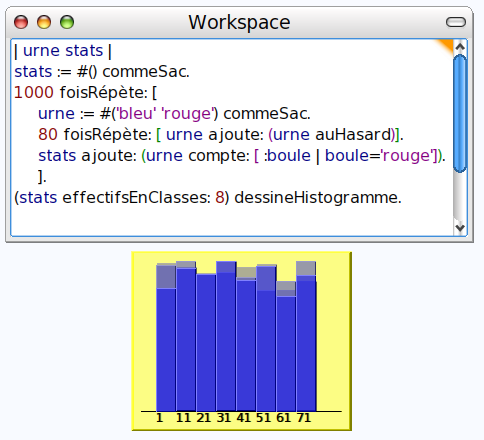
Comme le diagramme en bâtons des effectifs est peu lisible, on lui préfère un histogramme :

Modèle des urnes d'Ehrenfest

Avec deux urnes, l'une initialement vide

Règle du jeu : On tire au hasard une boule, repérée par un numéro (non lisible ci-dessous) et on la change d'urne. Initialement, toutes les boules sont dans l'urne bleue (à droite).

On s'intéresse à l'évolution à long terme: Y a-t-il une configuration d'équilibre ?

Simulation avec 200 boules

Évolution à plus long terme

Avec 4000 boules