Géry Huvent nous a aimablement communiqué un résultat classique du Wasan (mathématiques traditionnelles japonaises) qui est apparu comme la clé permettant de traiter simplement et efficacement le théorème des cercles inscrits égaux. Après la présentation de la nouvelle preuve qui en résulte, nous reviendrons, du point de vue didactique, sur les étapes de notre recherche.

Nouvelle preuve élémentaire du théorème des cercles inscrits égaux

Résultat préliminaire

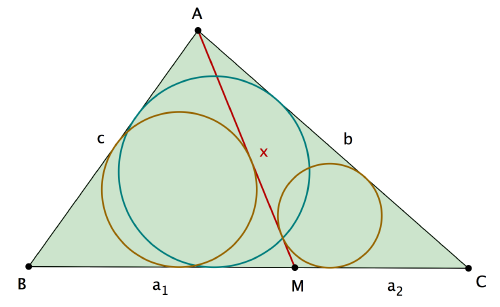
Soit un triangle ABC (de côtés a = BC, b = CA, c = AB) partagé en deux triangles ABM (de côtés $a_1=BM$, x = MA, c = AB) et AMC (de côtés $a_2=MC$, b = CA, x = AM). Si on note p, $p_1$, $p_2$ leurs demi-périmètres respectifs, on a

$p_1+p_2=\dfrac{1}{2} (a_1+x+c+a_2+b+x) =p+x.$

Pour éliminer x de cette relation, utilisons le fait que $\cos \widehat{AMB}+ \cos \widehat{AMC}=0$. Cela s’écrit successivement :

$\dfrac{a_1^2+x^2-c^2}{2a_1x}+\dfrac{a_2^2+x^2-b^2}{2a_2x}=0\ ;$

$\dfrac{(a_1+x)^2-c^2}{2a_1x}+\dfrac{(a_2+x)^2-b^2}{2a_2x}=2\ ;$

$2x=\dfrac{(a_1+x+c)(a_1+x-c)}{2a_1}+\dfrac{(a_2+x+b)(a_2+x-b)}{2a_2}\ ;$

$2x=\dfrac{2p_1(2a_1-2p+2p_2)}{2a_1}+\dfrac{2p_2(2a_2-2p+2p_1)}{2a_2}\ ;$

$x=\dfrac{p_1(a_1-p+p_2)}{a_1}+\dfrac{p_2(a_2-p+p_1)}{a_2}\ ;$

$x=p_1+p_2-\dfrac{pp_1}{a_1}-\dfrac{pp_2}{a_2}+\dfrac{ap_1p_2}{a_1a_2}.$

En reportant cette valeur de x dans la relation initiale $p_1+p_2=p+x$, on obtient

$p=\dfrac{pp_1}{a_1}+\dfrac{pp_2}{a_2}-\dfrac{ap_1p_2}{a_1a_2}.$

En multipliant les deux membres de l’égalité par $\dfrac{a_1a_2}{pp_1p_2}$, il vient successivement :

$\dfrac{a_1a_2}{p_1p_2}=\dfrac{a_2}{p_2}+\dfrac{a_1}{p_1}-\dfrac{a}{p}\ ;$

$1-\dfrac{a}{p}=1-\dfrac{a_1}{p_1}-\dfrac{a_2}{p_2}+\dfrac{a_1a_2}{p_1p_2}\ ;$

$\boxed{1-\dfrac{a}{p}=\left(1-\dfrac{a_1}{p_1} \right) \left(1-\dfrac{a_2}{p_2} \right)}\,.$

En notant R, $r_1$ et $r_2$ les rayons des cercles respectivement inscrits dans les triangles ABC, ABM et AMC, et h la hauteur commune issue de A de ces trois triangles, cette relation s’écrit aussi

$\boxed{1-\dfrac{2R}{h}=\left(1-\dfrac{2r_1}{h} \right) \left(1-\dfrac{2r_2}{h} \right)}\,.$

(car, par exemple dans le triangle ABC, l’aire S vaut $S=pR=\dfrac{1}{2}ah$, ce qui donne $\dfrac{a}{p}=\dfrac{2R}{h}$). On a ainsi une relation multiplicative simple entre le rayon du cercle inscrit dans le grand triangle et les rayons des cercles inscrits dans les deux petits.

Ce résultat se généralise immédiatement au cas d’un partage $(M_0=B, M_1, \dots, M_{n-1}, M_n=C)$ du segment [BC]. En notant $r_i$ le rayon du cercle inscrit dans le triangle $AM_{i-1}M_i$, il vient

$\boxed{1-\dfrac{2R}{h}=\left(1-\dfrac{2r_1}{h} \right) \left(1-\dfrac{2r_2}{h} \right) \dots \left(1-\dfrac{2r_n}{h} \right) }\,.$

En effet, il suffit d’appliquer le résultat obtenu pour deux triangles à $AM_0M_1$ et $AM_1M_2$, puis à $AM_0M_2$ et $AM_2M_3$, et ainsi de suite jusqu’à $AM_0M_{n-1}$ et $AM_{n-1}M_n$.

Le théorème des cercles inscrits égaux

Considérons maintenant un partage $(M_0=B, M_1, \dots, M_{n-1}, M_n=C)$ tel que $r_1=r_2=\dots=r_n$, c’est-à-dire tel que tous les triangles $AM_{i-1}M_i$ aient des cercles inscrits de même rayon, que nous allons noter r. On a alors

$1-\dfrac{2R}{h}=\left( 1-\dfrac{2r}{h} \right)^n,$

soit encore

$r=\dfrac{h}{2} \left( 1- \left(1-\dfrac{2R}{h} \right)^{1/n} \right),$

ou, pour revenir à une expression en fonction des côtés (sachant que $p=(a+b+c)/2$ et $S=\sqrt{p(p-a)(p-b)(p-c)}$),

$\boxed{r=\dfrac{S}{a} \left( 1- \left(1-\dfrac{a}{p} \right)^{1/n} \right)}\,.$

Si l’on considère maintenant un triangle de la forme $AM_iM_{i+k}$ formé de k triangles consécutifs du partage, avec $k \geq 2$, et si l’on note $r_{i,k}$ le rayon de son cercle inscrit, on a

$1-\dfrac{2r_{i,k}}{h}=\left( 1-\dfrac{2r}{h} \right)^k = \left( 1-\dfrac{2R}{h} \right)^{k/n},$

soit encore

$\boxed{r_{i,k}=\dfrac{S}{a} \left( 1- \left(1-\dfrac{a}{p} \right)^{k/n} \right)}\,.$

Ce rayon ne dépend pas de i, donc tous les triangles $AM_iM_{i+k}$ ont des cercles inscrits de même rayon.

Retour didactique sur notre cheminement

Une conception traditionnelle de la communication en mathématiques nous conduirait naturellement à supprimer l’article précédent, aussi laborieux qu’obscur, pour ne laisser sur le site que cette preuve, si rapide, directe et claire.

Mais, en tant que formateurs d’enseignants, nous rencontrons là l’occasion rêvée d’une « narration de recherche » mettant en évidence le cheminement vers une démonstration, l’évolution des représentations d’un problème au fur et à mesure de son appropriation, ou encore l’implicite des données comme obstacle primordial au dépassement d’une situation. Si le sujet n’est bien sûr pas nouveau, son domaine d’application est intéressant : alors que généralement on propose ce type d’analyse sur de grands problèmes historiques où la part de difficulté ontologique relativise la dimension didactique, ici, sur un cas concret élémentaire, avec comme sujets des enseignants ordinaires aux prises avec des mathématiques déjà largement parcourues, nous proposons une analyse que chacun pourra transférer sur ses élèves et leurs difficultés à chercher en classe.

En effet, en formation initiale des enseignants, il est parfois difficile de convaincre les futurs collègues des difficultés éprouvées par les élèves à entrer aussi rapidement que le laissent supposer les programmes dans les concepts engagés au collège ou au lycée. C’est pour cela que nous avons choisi d’analyser, à des fins de formation et de transposition didactique, sur le cas simple de ce problème, notre propre comportement et le difficile travail de compréhension des preuves tant que l’on n’a pas trouvé la clé de cette compréhension.

La recherche préliminaire de la longueur AM dans le cas n = 2

Tout d’abord, on peut constater une nouvelle fois que, même pour des enseignants, la façon dont le problème est posé exerce une influence durable sur l’orientation des recherches.

L’article de Tangente, à propos du problème des cercles inscrits égaux, donnait deux indications. Tout d’abord on précisait ce qu’était une preuve élémentaire : cela signifiait ici « sans sinus hyperbolique ». Ensuite, « pour prendre un bon départ », la revue invitait à calculer la longueur du segment de partage d’un triangle en deux triangles ayant des cercles inscrits égaux.

Après coup, on voit bien que la contrainte d’élémentarité contenait une information précieuse sur la nature du problème : si une fonction hyperbolique devait débloquer facilement la situation, on aurait pu en déduire que le problème relevait d’un processus d’exponentiation sur ses données géométriques, qu’il s’agissait de transformer une somme (les aires de la réunion de deux triangles contigus de sommet A, c’est immédiat) en un produit, à mettre en évidence, utilisant les rayons des cercles inscrits :

si on note $\omega_A(T) = 1-\dfrac{2r}{h}$, le lemme initial de cette page dit que $\omega_A(T_1 \cup T_2) =\omega_A(T_1)\,\omega_A(T_2)$.

Mais, en fait, nous n’avons vu cette information qu’au moment de conjecturer la formule des $r_{n,k}$. Et, comme nous allons le voir plus loin, sans en tirer toutes les conséquences.

Par ailleurs, la seconde indication de Tangente nous a pour longtemps orientés vers le calcul de AM, puis, dans le cas général, vers celui des $AM_{i}$ et de leur somme, en nous détournant curieusement des rayons des cercles inscrits, grandeurs naturelles qui auraient dû s’imposer d’elles-mêmes à notre attention puisqu’elles figuraient explicitement dans l’énoncé du problème !

Dès le début, l’expression de la longueur AM du segment de partage pour le cas de deux cercles, même si elle est présentée de manière concise dans les calculs de Jean Marc et Dominique, n’est pas évidente à trouver. De plus, cette valeur est tout de suite perçue comme non pertinente par Yves du point de vue de la géométrie dynamique. Malgré cela, nous persistons aveuglément dans cette voie, l’aide initiale se transformant en obstacle durable.

La première preuve par récurrence

Il est alors intéressant d’observer les articulations entre les motivations et la prégnance des représentations du problème, puis le détachement de ces représentations et leur remplacement par des nouvelles.

La motivation chez Yves est d’abord constructive. Il y a chez lui comme un implicite dynamique — on le voit clairement dans d’autres articles — selon lequel un résultat géométrique sera d’autant mieux compris qu’on saura le traduire en une construction dynamique. En pratique, ce principe (dont on va voir très vite les limites) se traduit tout simplement par une analyse spécifique de la situation pour qu’une solution permette une construction dynamique.

Dans cette optique, le cas n = 2 invite à un regard barycentrique sur M qui aboutit rapidement à une construction — d’autant plus vite que ses collègues lui apportent la valeur de AM sur un plateau. Sa transformation en macro donne des constructions pour les puissances de 2, sans soulever de question, dans un premier temps, sur l’égalité de tous les rayons. La simple poursuite des calculs dans cette voie aboutit à un système de deux équations du troisième degré pour le cas n = 3 :

$(1)\quad (x+b-2y)(2x+2y+b+c)^2 = a^2(x+b+2y)$,
$(2)\quad (y+c-2x)(2x+2y+b+c)^2 = a^2(y+c+2x)$,

dans lequel on voit bien les rôles symétriques de b et c pour les calculs respectifs de x et y, mais sans que l’on puisse réellement exploiter cette symétrie puisque justement on va calculer une seule des deux variables par ce système, l’autre étant donnée par une relation élémentaire du second degré grâce au cas n = 2 toujours applicable dans une partie de la figure.

Le principe implicite dynamique s’est alors transformé en un acharnement dynamique à construire la figure à partir des seules données a, b et c. Puisque la figure a été faite, cet épisode peut encore servir à illustrer la robustesse du logiciel utilisé. On peut le vérifier rapidement sur la figure placée dans le bloc dépliable suivant :

Voir la solution algébrique pour n = 3

<carmetal|doc=1543|largeur=739|hauteur=518>

Les formules que l’on voit dans cette figure montrent bien l’impasse d’un calcul individuel des longueurs des segments de partage pour la construction, mais par ailleurs les calculs barycentriques associés montrent, quant à eux, une régularité récurrente encourageante. Il est très simple d’exprimer les coordonnées barycentriques des points $M_i$ en fonctions des longueurs $x_i$. La motivation constructive initiale se transforme alors, par défaut, en une motivation uniquement démonstrative, à l’encontre du principe qui l’a fait naître : des relations symétriques entre les variables vont permettre une preuve par récurrence purement formelle sans aucune possibilité constructive.

Dans ce mouvement de la motivation, on observe tout d’abord une distanciation vis à vis des longueurs $x_i$ : non seulement on a renoncé à les construire, mais on ne cherche même pas les systèmes d’équations dont elles sont racines, dans la mesure où des relations symétriques en les seules variables $x_1$ et $x_{n-1}$ suffisent à la preuve. Il y a en même temps un attachement à ces variables, à cette démarche, pourtant totalement opaque, parce que l’on sent bien qu’elle va aboutir à une preuve. Et effectivement, en cherchant la relation que doivent vérifier ces variables pour que le théorème soit vrai, on parvient à une relation que l’on peut montrer assez rapidement par récurrence.

Dans un récent article du site Image des mathématiques, un mathématicien rappelait que son travail n’était pas tant de démontrer des théorèmes que de comprendre les démonstrations qu’il écrivait. Manifestement nous sommes encore loin d’un tel objectif. L’opacité que l’on ressent en lisant cette première preuve, par ailleurs élémentaire et séduisante puisqu’elle repose sur des relations entre les coefficients sans aucun calcul explicite, est à la mesure de la distance entre, d’une part, l’approche retenue, le choix des variables, l’expression du problème par ces variables et, d’autre part, les véritables enjeux du problème, dans son rapport à l’exponentiation.

Ainsi, sur cet exemple d’un théorème de géométrie, élémentaire mais éloigné de notre culture, on voit qu’un jeu d’écriture finement mené peut aboutir à une preuve de ce que l’on cherche sans véritablement dégager d’idée pertinente, ni de piste menant à la raison géométrique profonde du résultat.

Le calcul des rayons $r_{n,k}$

Devant ces limites, en particulier pour donner une dimension constructive à cet article... de géométrie dynamique, Dominique prend une autre direction et se propose de calculer le rayon des cercles inscrit égaux, que l’on appellera $r_{n,1}$ par la suite. Afin de mieux prendre en compte les rôles symétriques joués par b et c, il décide de travailler avec p et p - a.

Une réécriture dans cette direction donne rapidement le résultat pour le cas n = 2. Il s’ensuit assez laborieusement un premier traitement exploratoire par radicaux du cas n = 4, qui est perçu comme allant de soi même s’il est un peu technique.

Première version du calcul pour n = 4

En écrivant comme précédemment que l’aire du triangle ABC est la somme des aires des quatre petits triangles, on dégage la formule de base :

$r_{4,1}=\frac{S}{p+AM_1+AM_2+AM_3}.$

En supposant acquis que les cercles inscrits dans les triangles $ABM_2$ et $AM_2C$ ont même rayon, on sait déjà que $AM_2=\sqrt{p(p-a)}$. Reste à calculer $AM_1$ et $AM_3$. Pour cela, on aura besoin de la valeur de $BM_2$, qui est un sous-produit immédiat du calcul de $AM_2$ :

$BM_2=\frac{b-c}{a}\sqrt{p(p-a)}+\frac{2p(p-b)}{a}-c$.

Le demi-périmètre $p’$ du triangle $ABM_2$ est alors :

$p’=\frac{1}{2} (AB+BM_2+AM_2)=\frac{\sqrt{p}}{a} \left[ (p-b)\sqrt{p}+(p-c)\sqrt{p-a}\, \right].$

Il vient ensuite :

$p’-BM_2=\frac{\sqrt{p-a}}{a} \left[ (p-b)\sqrt{p}+(p-c)\sqrt{p-a}\, \right]$ ;

$AM_1=\sqrt{p’(p’-BM_2)}=\frac{p^{1/4}(p-a)^{1/4}}{a} \left[ (p-b)\sqrt{p} + (p-c)\sqrt{p-a}\, \right].$

De façon analogue, en permutant b et c, on obtient la valeur de $AM_3$ :

$AM_3=\frac{p^{1/4}(p-a)^{1/4}}{a} \left[ (p-c)\sqrt{p} + (p-b)\sqrt{p-a}\, \right],$

d’où : $AM_1+AM_3=\frac{p^{1/4}(p-a)^{1/4}}{a} (a\sqrt{p}+a\sqrt{p-a})=p^{3/4}(p-a)^{1/4}+p^{1/4}(p-a)^{3/4}.$

Finalement :

Fin du bloc dépliable

Dans cette première version du cas n = 4, l’expression comme puissance dans $\omega_A(T)$ n’est pas encore mise à jour.

Le cas n = 3 s’avère ensuite autrement plus redoutable, pour les raisons exposées plus haut. Dans un premier temps, comme chez Yves, toutes les tentatives pour calculer individuellement $x=AM_1$ et $y=AM_2$ conduisent à des équations algébriques inextricables. La solution apparaît lorsque Dominique prend conscience que c’est seulement la somme x + y des deux segments de partage qui intervient. Celle-ci est bien sûr symétrique pour le problème et donc s’exprime à partir de p et p-a dans une équation du troisième degré beaucoup plus simple, qui se laisse résoudre explicitement. La solution prend la même forme que dans les cas n = 2 et n = 4, ce qui est certes satisfaisant, puisqu’il en résulte une conjecture générale des plus plausibles, mais aussi décourageant, car on se rend bien compte que, sauf simplifications insoupçonnées, on ne pourra plus résoudre de façon analogue des équations par radicaux à partir du degré 5.

Cependant, sur le plan dynamique, la formule trouvée résout totalement la question : on peut construire les figures pour tout partage, très aisément, ce qui, en définitive, même si ce n’est pas lié, mais parce que c’était l’objectif initial, participe au renforcement de la représentation que nous avons à ce moment du problème.

Peu après, Dominique met en évidence la forme puissance de sa formule pour $r_{n,1}$, ce qui conduit à une autre approche bien plus synthétique pour le calcul de $r_{4,1}$. Avec cette seconde formule, simple, belle et concise, la perception du problème dans un rapport à l’exponentiation était désormais dégagée, sans pour autant que ce rapport devienne consciemment la clé du problème.

Cette première perception aide néanmoins à voir plus loin et, en particulier, à mener le calcul de $r_{n,k}$, démontré rapidement par des considérations sur les puissances et des rapports d’aire égaux : puisque les formules obtenues sont des formules de puissance, les représentations que l’on a du problème, pour bien plus claires qu’elles soient, sont de l’ordre des propriétés multiplicatives des puissances. Cette nouvelle approche est renforcée par les succès auxquels elle a conduit : elle a donné la clé du calcul des $r_{n,k}$ et elle a grandement simplifié la nouvelle preuve pour le cas n = 4. En outre, même si on s’éloigne quelque peu de l’objectivité, la formule obtenue possède, en elle-même, un condensé esthétique auquel un mathématicien n’est pas insensible, comme si le beau, in fine, était aussi un argument en soi... sans que l’on sache exactement quel rapport aux mathématiques cet argument exprime.

Intermède

On peut dégager un invariant de ces deux approches. Dans les deux cas, la volonté d’aboutir permet à chaque auteur de créer des pistes qui aboutissent à ce qu’ils veulent, mais qui chacune, parce qu’elles aboutissent, renforcent leurs auteurs dans leurs représentations : Yves, parce qu’il arrive à sa relation de récurrence, est pris dans ses obscures relations barycentriques entre toutes les variables qui n’ont aucune chance de donner l’ombre d’une explication à ce problème. Dominique, parce que sa formule concise a permis de se dégager d’une somme complexe, difficile à manipuler, et qu’elle est la clé du calcul des $r_{n,k}$, a désormais une vision multiplicative du problème : les puissances sont vues dans leur relations multiplicatives, mais pas dans leur relation à l’addition des aires.

La preuve des $r_{n,1}$

Il en résulte une grande difficulté pour démontrer la valeur des $r_{n,1}$ pour tout n. On voit bien que l’on a des relations de produit : si la formule est vraie pour $r_{p,1}$ et $r_{q,1}$, alors elle est vraie pour $r_{pq,1}$ par le même calcul que pour les $r_{n,k}$, mais comment passer de n - 1 à n, ou de n - 2 et n - 1 à n ? À ce moment de la recherche, on ne perçoit plus le problème que dans un regard multiplicatif : il suffirait de montrer le résultat pour les nombres premiers, mais cela n’a aucune chance d’aboutir simplement (le cas n = 5 paraît déjà très complexe à traiter "à la main"). Par ailleurs, l’échec de plusieurs tentatives de type additif renforce, implicitement, la représentation multiplicative.

Ce point est facilement transférable dans des situations scolaires : c’est typiquement le cas où, par des manipulations diverses que l’on croit nouvelles, on réutilise des variantes de ce que l’on sait déjà pour retrouver en définitive que 0 = 0 (par exemple). Le manque d’idées nouvelles renforce, malgré nous, l’idée qu’il n’y en a pas et qu’il faut persévérer dans sa représentation. Heureusement, l’acharnement humain a lui aussi une certaine efficacité... mais à quel prix ?

Cliquer pour une anecdote sur la confiance relative à l’expérimentation

Dominique avait des difficultés à conclure... Yves repense à cette proposition "le montrer pour les premiers"... mais on s’est tellement trompé sur les nombres premiers (de Fermat, etc.)... Pour couronner le tout, il tombe à ce moment-là sur un article qui parle des limites de l’expérimentation avec ce bel exemple de Jean Paul Delahaye (Complexités, Belin, p. 234) qui dit que la formule

est vraie pour n allant de 1 à 6, ce qui laisse à penser que l’égalité est probablement vraie pour tout n. Mais elle ne l’est pas pour n = 7...

Yves se met alors à vérifier expérimentalement la formule des $r_{n,1}$ pour les premiers nombres premiers comme ci-dessous pour 17 :

<carmetal|doc=1544|largeur=735|hauteur=502>

Ce qui a fait dire à Dominique dans un éclat de rire, en contre-pied de l’exemple de Delahaye : "ce n’est pas non plus parce qu’on n’arrive pas complètement à démontrer une formule qu’elle est fausse !" Naïveté de la confusion du champ expérimental en face d’une détermination renforcée à montrer la relation...

Fin du bloc dépliable

Dominique entreprend alors la résolution par récurrence avec cette approche de la manipulation sur les racines n-ièmes : passer de n - 2 et n - 1 à n par un jeu de manipulations sur les puissances. Ainsi est-il amené à exprimer, en fonction de ses données symétriques, la somme $x=\displaystyle{\sum_{k=1}^{n-1}AM_{k}}$. Pour cela, il met en évidence un coefficient q, invariant des trois triangles en jeu dans sa récurrence, qui n’est autre que le $\omega_A(T)$ du lemme énoncé plus haut. Il s’ensuit alors un calcul assez subtil pour arriver, par un jeu des combinaisons de ces trois triangles à exprimer la somme x dans deux relations linéaires où il ne restera que deux inconnues, dont x. Ce calcul un peu complexe se termine par cette phrase : "Il ne reste plus qu’à revenir progressivement aux notations initiales".

En analysant avec un peu de recul cette démonstration, on peut mettre en évidence un processus assez récurrent en mathématiques. Bien entendu, on ne peut pas parler de "recherche en mathématiques" dans ce travail sur un problème japonais du XVIe siècle, mais pour nous, comme pour des élèves, il s’agissait d’un problème nouveau et on voit ici, comme on peut le voir historiquement dans d’autres preuves mathématiques, un phénomène assez classique : pour parvenir à sa preuve, l’auteur va centrer, de fait, sa démonstration sur l’élément clé du problème (ici le coefficient q dont on a vu qu’il est le cœur du lemme crucial), mais ne voyant cet élément que dans son aspect technique, comme un catalyseur de preuve (ici, il permet d’exprimer x, toujours perçu, lui, comme le nœud du problème), il l’élimine aussitôt pour revenir à son questionnement initial.

Dominique revient donc progressivement "aux notations initiales" et aboutit (après quelques longs jours d’efforts) à la preuve de la formule des $r_{n,1}$, qui, elle-même, contient la preuve du TCIE.

Une transposition comme enjeu de formation

On sait qu’il est souvent difficile d’illustrer le travail des mathématiciens, car les concepts en jeu sont généralement difficiles d’accès (on pense, par exemple, à la preuve de Wiles du théorème de Fermat). Ici, un travail de mathématicien — toutes proportions gardées avec un vrai travail de chercheur en mathématiques — serait, en analysant cette preuve, de s’apercevoir que ce coefficient q, perçu comme expression transitoire focalisant les calculs intermédiaires, est en fait un élément important de ce qui est en jeu.

Lors de la mise en ligne de cette preuve, même si nous avons vu les liens entre les deux preuves, notre représentation totalement multiplicative du problème n’a pas varié. Plus précisément, le passage par les sommes était vu comme un détournement complexe et technique nécessaire parce que l’on n’avait rien trouvé d’autre qu’une preuve par récurrence d’un phénomène essentiellement multiplicatif.

On voit là que si les représentations initiales du problème ont évolué, quand ces représentations donnent des fruits, elles ont tendance à s’ancrer dans la légitimité acquise du fait même de leur succès. Les pistes possibles vers une évolution de ces représentations, seulement perçues en tant qu’épiphénomènes techniques dépourvus de véritable sens mathématique, sont alors inconsciemment évacuées.

De façon générale, il est fréquent qu’une connaissance soit si longue et difficile à installer qu’elle résiste ensuite à tout progrès, cela d’autant plus qu’une représentation s’est déjà révélée assez solide pour produire des résultats de manière durable. Il en est ainsi de tous les changement de paradigmes mathématiques, que ce soit à l’école, avec le passage des entiers aux décimaux (et le concept implicite sous-jacent de densité), au collège, dans la difficile transition de l’arithmétique à l’algèbre, au lycée, avec les approches fonctionnelles (théorèmes locaux et globaux), ou à l’université, quand les structures algébriques s’appliquent à des espaces fonctionnels topologiques.

Dans tous ces cas, une connaissance bien établie, déjà pertinente, efficace et fructueuse est soit mise en défaut, soit balayée par d’autres concepts plus riches. Le travail essentiel des enseignants est alors d’accompagner ces changements de paradigmes et de dégager les passages procéduraux pertinents d’un champ conceptuel à un autre, plutôt que de simplement présenter des connaissances nouvelles de manière concise et élégante, ce à quoi on voudrait parfois résumer notre métier.

En ce qui nous concerne, sans vouloir aucunement nous dédouaner, les enjeux n’étaient certes pas les mêmes et le contexte non plus : après avoir chacun consacré une bonne partie des vacances à l’étude du TCIE dans un contexte de loisir et non d’apprentissage, il fallait passer à autre chose tout simplement. Malgré tout, il est intéressant de noter que la démonstration du théorème de deux manières différentes n’a pas engendré une véritable remise en cause des représentations ayant conduit à ces preuves.

La preuve par la trigonométrie hyperbolique

Contacté comme spécialiste bien connu des Sangaku, Géry Huvent, sans même avoir l’information de Tangente à propos d’une approche hyperbolique possible, voit tout de suite l’intérêt de passer par les sinus hyperboliques. Pourquoi ? "Parce que, dans cette situation, c’est un changement de variable que j’impose à mes élèves." Son calcul du rayon du cercle pour un partage en n donne alors, avec $t_{k}=\arg\text{sh}(x_{k}/h)$ dans son repère, $r =\dfrac{h}{2}\times\left( 1-\exp\left( t_{k-1}-t_{k}\right) \right).$ D’où la suite arithmétique des $t_{k}$ et la raison $\rho=-\ln\left( 1-\dfrac{2r}{h}\right)$ qui n’est autre que $-\ln\left( \omega_A(T)\right).$

Il s’agit là d’une première approche de Géry. Sa démonstration analytique, faite rapidement après la lecture de notre article mis en ligne, est technique, avec pour objectif premier de montrer plus simplement le résultat proposé par Dominique. On notera effectivement que c’est une preuve directe, sans récurrence.

La preuve de Géry en général et cette expression de r en particulier montrent bien que, dans ce problème, il y a davantage un rapport à l’exponentiation qu’un simple rapport mutliplicatif à la puissance. Chacun le sent, mais ce rapport reste encore flou, comme mis en évidence (produit ?) par ce changement de variable des $t_{k}$, loin des préoccupations géométriques initiales. L’article de Tangente lui-même ne comportait-il pas d’ailleurs cette phrase : "À se frotter au problème on en vient à se demander si la question est de nature géométrique" ?

Si chacun est assez émerveillé — en fait plus qu’autre chose — devant la mise en évidence de la raison arithmétique et de son lien direct avec la valeur de q de la preuve de Dominique, il est encore trop difficile de voir dans ce terme $\omega_A(T)$ autre chose qu’un invariant technique.

Les limites du cas particulier

Il faut probablement en chercher la raison dans un autre point important de la compréhension des mécanismes qui sous-tendent une preuve : la généralisation d’un cas particulier.

Avant que Géry ne s’aperçoive, en fouillant dans sa documentation sur les Sangaku, qu’en fait ce résultat est la conséquence, assez banale en définitive, d’un résultat plus général, nous nous étions tous bien entendu focalisés sur les données initiales du théorème, à savoir les cercles inscrits égaux. Or la véritable compréhension des enjeux du problème est dans le rapport entre les données quand les cercles ne sont pas égaux (c’est encore le lemme ci-dessus)... On se retrouve ainsi dans l’un des changements de paradigme cités plus haut, à savoir le passage du statique (local) au variationnel (global) qui, lui, va fournir de nouvelles clés. L’exponentiation dans sa globalité fonctionnelle, comme vue dans la relation des $\omega_A(T),$ n’était pas perceptible, car il n’y avait pas de variation sur les rayons.

Ce lemme, vite démontré avec nos arguments élémentaires usuels (au final, on n’utilise rien d’autre que la formule d’Al-Kashi), est effectivement la clé du théorème comme le voit dans la preuve publiée en tête de l’article : des rayons variables confèrent tout leur sens au cas particulier des rayons égaux et à la forme que l’on a trouvée pour les $r_{n,1}.$ (Voir aussi une version épurée de la preuve par la trigonométrie hyperbolique sur le site de Géry Huvent.)

Cet exemple est une belle illustration de la difficulté à trouver certains résultats quand ils ne sont que des cas particuliers de résultats plus généraux. Ici, il ne nous serait pas venu rapidement à l’esprit de faire varier les rayons des cercles pour un résultat plus simple. Et pourtant, faire varier des données pour dégager un invariant est habituel en géométrie dynamique, voire, plus généralement, en mathématiques. Cependant, nous étions dans des représentations qui cherchaient une valeur précise, solution d’un problème bien particulier : même nos outils contemporains d’investigation ne pouvaient nous être utiles, car nous n’avancions pas sur la bonne voie.

Conclusion

La compréhension des propriétés géométriques qui sont à la base du théorème des cercles inscrits égaux n’est pas venue des découvertes personnelles des auteurs des deux preuves précédentes. En définitive, les formateurs se sont retrouvés dans la situation que vivent quotidiennement leurs étudiants : après avoir cherché longtemps avec leurs connaissances premières et trouvé des solutions aussi longues que maladroites, une autre solution, élémentaire, élégante, construite sur un concept différent, arrive de l’extérieur...

En la circonstance, bien que rompus à la géométrie "occidentale" du triangle, faite de droites concourantes ou parallèles, de points alignés ou cocycliques, nous avons eu du mal à entrer dans le monde des Sangaku, cette autre géométrie du triangle dans laquelle un triangle est avant tout un polygone plein, avec pour objets fondamentaux son aire, son périmètre et son cercle inscrit. Tout notre arsenal personnel de connaissances géométriques et algébriques s’est soudain révélé peu pertinent face à un monde étranger dont les ressorts cachés étaient différents.

L’expérience fut incontestablement enrichissante : nous avons vécu ce que vit un élève chaque fois qu’il aborde un nouveau chapitre du programme dont les clés lui sont encore inconnues. Comment ne pas être persuadés après cela qu’il est important de faire travailler les élèves sur des problèmes ouverts, de leur laisser un temps très important de recherche, de reconnaître enfin leurs tâtonnements, expérimentations, conjectures et erreurs comme significatifs d’une activité scientifique véritable méritant d’être valorisée ? On a trop tendance, dans l’enseignement, à se centrer sur un seul aspect du travail mathématique, celui qui consiste à démontrer un résultat aux contours bien identifiés, donné directement par le professeur sous une forme épurée. À ce propos, les narrations de recherche, comme celle que nous avons tenté de rédiger, sont justement des activités expérimentées dans certaines classes et analysées dans certains IREM, en tant qu’outil pour diversifier le travail mathématique et exercer les élèves à un retour réflexif permanent sur leur pratique.