ÉTUDE MATHÉMATIQUE DES NOMBRES MÉTALLIQUES : des proportions harmonieuses d’Euclide à leurs équations caractéristiques et définitions de leurs suites associées

• démarche ..... le nombre d’or ..... le nombre d’argent ..... le nombre de cuivre ..... le nombre de nickel ..... le nombre de cobalt
• coefficients des suites associées ...définition de la suite associée ..... approximation des nombres métalliques (programme en python)
• Limite des nombres métalliques ..... fractions engendrées par les nombres métalliques

RECTANGLES MÉTALLIQUES

• étude du rectangle d’argent ....étude du rectangle de cuivre

SPIRALES MÉTALLIQUES

• la spirale d’or ....... la spirale d’argent ....... étude des rayons d’une spirale métallique ....... la spirale de cuivre ....... trilogie de spirales métalliques

FIGURES MÉTALLIQUES

• les rectangles métalliques ....... les losanges métalliques .......les coquillages métalliques
• les ellipses métalliques centrées ....... les ellipses métalliques non centrées ....... les cœurs métalliques

- I. MÉTHODE GÉNÉRALE D’APPROXIMATION DES NOMBRES MÉTALLIQUES

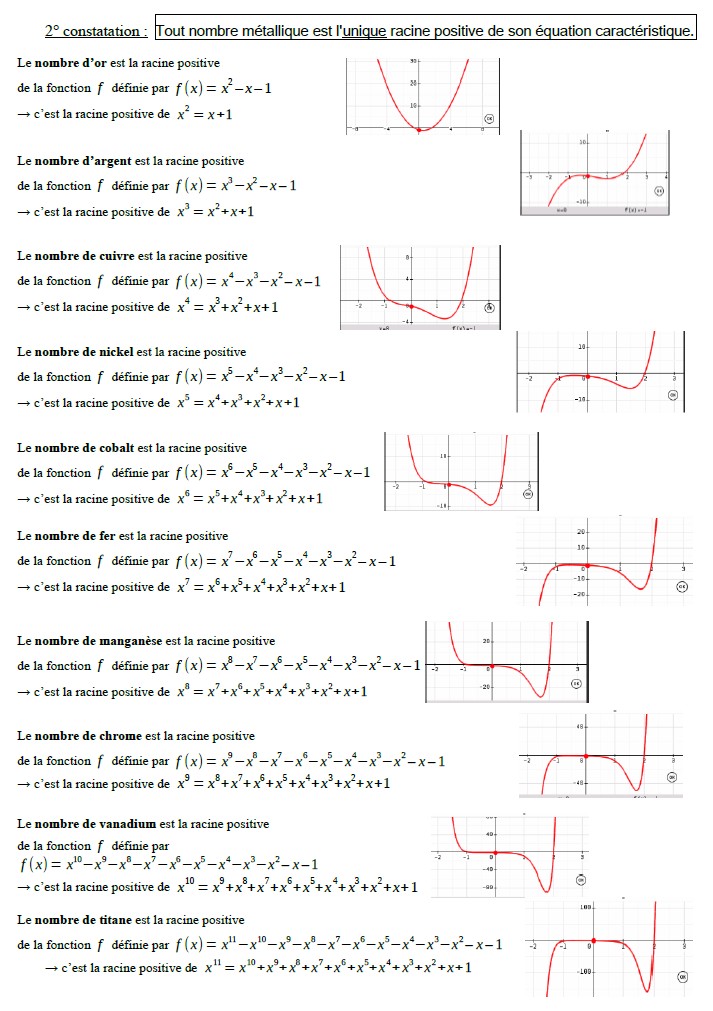
• 2. LE NOMBRE D’OR : DE LA PROPORTION D’EUCLIDE A LA SUITE DE FIBONACCI ..................................................................................................

  

  

• 3. LE NOMBRE D’ARGENT : DE LA PROPORTION D’EUCLIDE A LA SUITE DE TRIBONACCI .................................................................................................

  

  

• 4. LE NOMBRE DE CUIVRE : DE LA PROPORTION D’EUCLIDE A LA SUITE DE QUARTBONACCI ..........................................................................................

  

• 5. LE NOMBRE DE NICKEL : DE LA PROPORTION D’EUCLIDE A LA SUITE DE QUINTEBONACCI ...................................................................................

  

• 6. LE NOMBRE DE COBALT : DE LA PROPORTION D’EUCLIDE A LA SUITE DE SIXBONACCI ........................................................................................

  

• 7. OBSERVATION ET ÉTUDE DES COEFFICIENTS DES SUITES ASSOCIÉES AUX NOMBRES MÉTALLIQUES ........................................................................

• 8. DÉFINITION DES COEFFICIENTS DES SUITES ASSOCIÉES AUX NOMBRES MÉTALLIQUES.................................................................................................

  

• 9. APPROXIMATION DES NOMBRES MÉTALLIQUES .................................................................................................

  

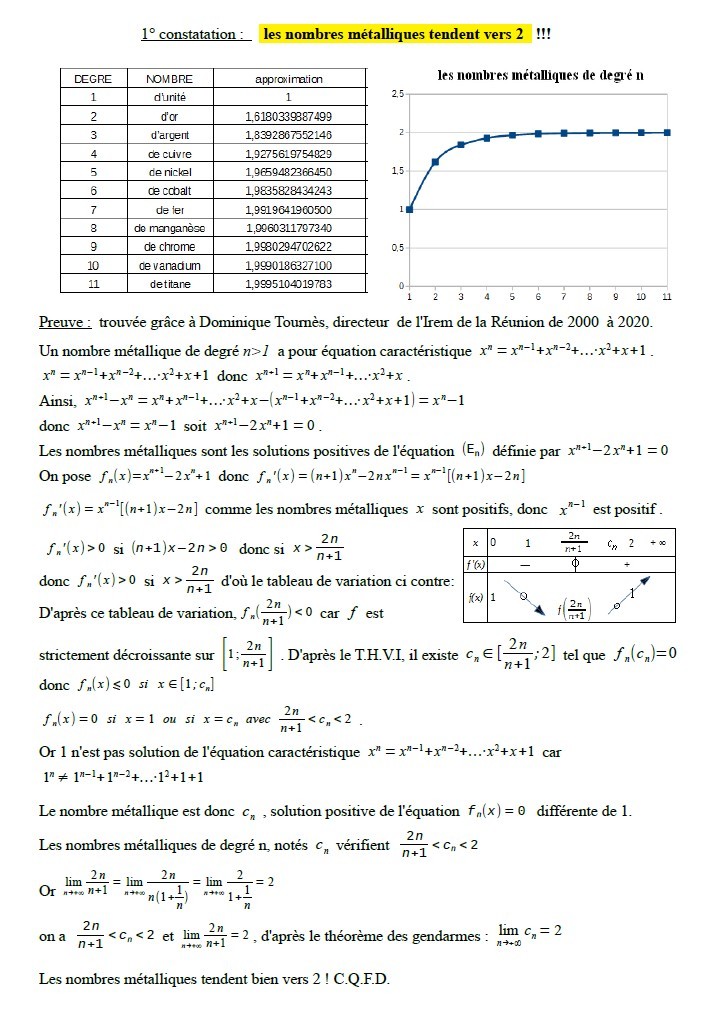
• 10. LIMITE DE LA SUITE DES NOMBRES MÉTALLIQUES .................................................................................................

  

  

• 11. FRACTIONS ENGENDRÉES PAR LES NOMBRES MÉTALLIQUES .................................................................................................

- II. LES RECTANGLES MÉTALLIQUES

.... TOUTES LES FIGURES ONT ÉTÉ RÉALISÉES A L’AIDE DU LOGICIEL CARMÉTAL

• • 1. ÉTUDE DU RECTANGLE D’ARGENT ........................................................................

    

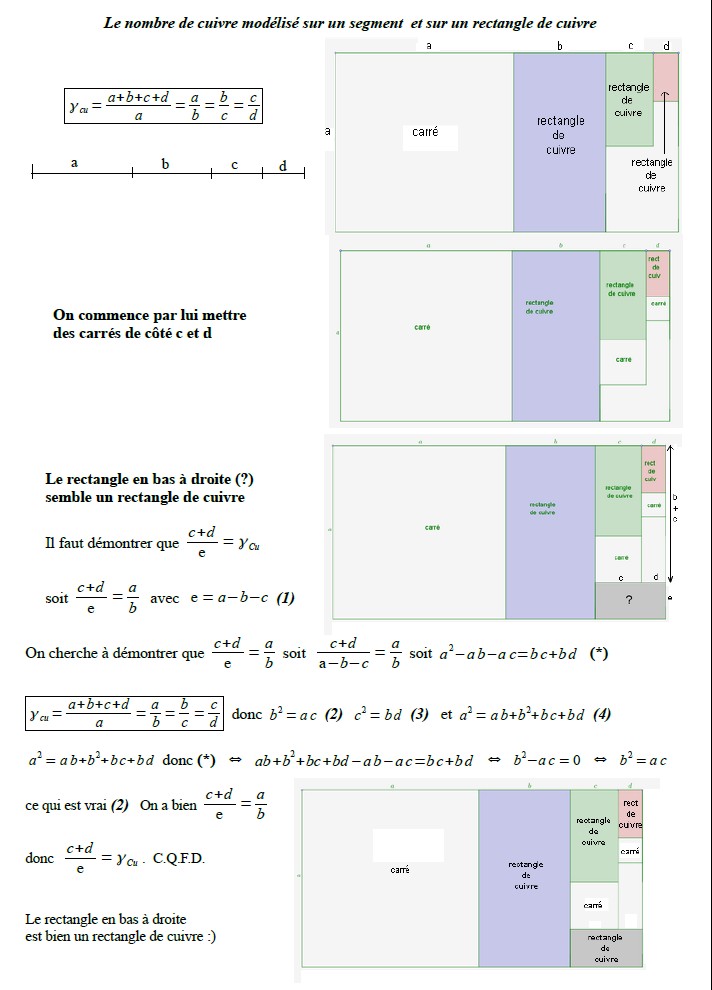
• • 2. ÉTUDE DU RECTANGLE DE CUIVRE........................................................................

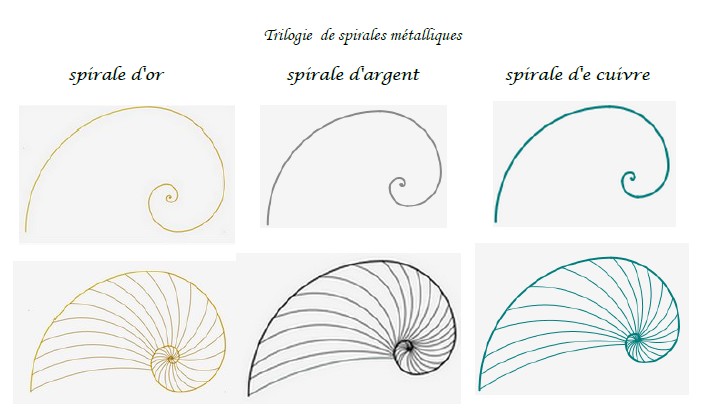
- III. LES SPIRALES MÉTALLIQUES

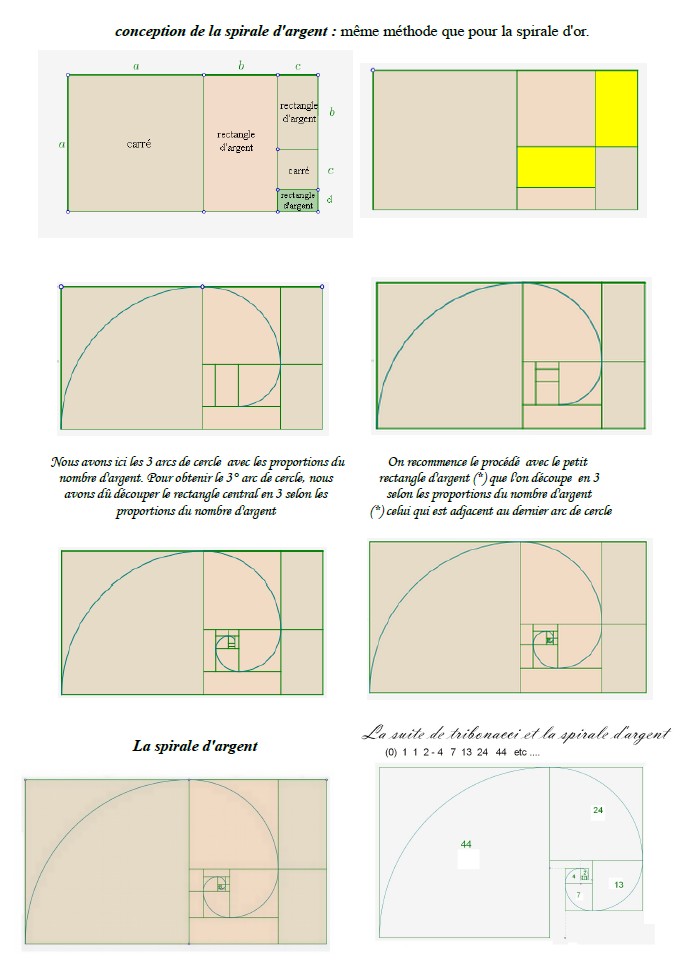
Les spirales métalliques sont constituées d’arcs de cercle dont les longueurs respectent les rapports de proportion des nombres métalliques.

• • 1. LA SPIRALE D’OR

    

• • 2. LA SPIRALE D’ARGENT

    

• • 3. ÉTUDE DES RAYONS DES SPIRALES MÉTALLIQUES

Pour créer la spirale de cuivre, il faut que les quatre premiers rayons utilisent les proportions du nombre métalliques de cuivre.
Afin de réaliser la spirale de cuivre sous le logiciel car métal, il faut savoir déterminer les longueurs des rayons successifs de la spirale de cuivre. Une étude s’impose :

• • 3. LA SPIRALE DE CUIVRE

    

  • 4. TRILOGIE DE SPIRALES MÉTALLIQUES

  • 

- IV. AUTRES FIGURES MÉTALLIQUES

• • 1. LES RECTANGLES MÉTALLIQUES ......................................................................

    

• • 2. LES LOSANGES MÉTALLIQUES ........................................................................

    

• • 3. LES COQUILLAGES MÉTALLIQUES ........................................................................

    

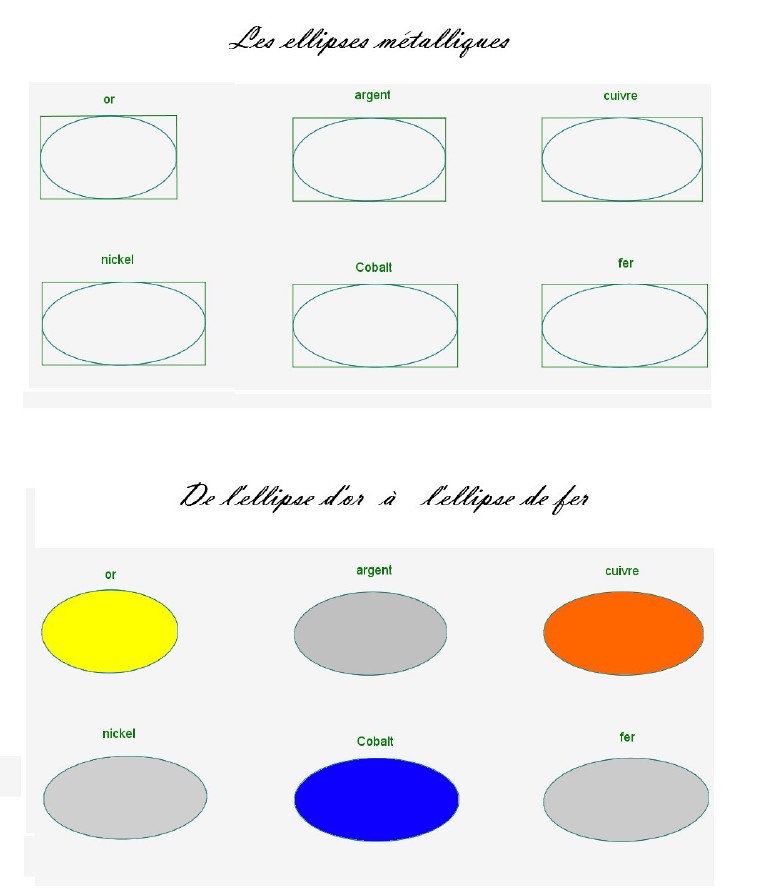
• • 4. LES ELLIPSES MÉTALLIQUES CENTRÉES ........................................................................

ici, on prend les milieux des côtés d’un rectangle métallique et un cinquième point de manière à obtenir une symétrie centrale de centre O, si O est le centre du rectangle.

• • 5. LES ELLIPSES MÉTALLIQUES NON CENTRÉES ........................................................................

Pour définir une ellipse, il faut 5 points.

Ici, on prend les milieux des côtés d’un rectangle métallique et un sommet du rectangle métallique.

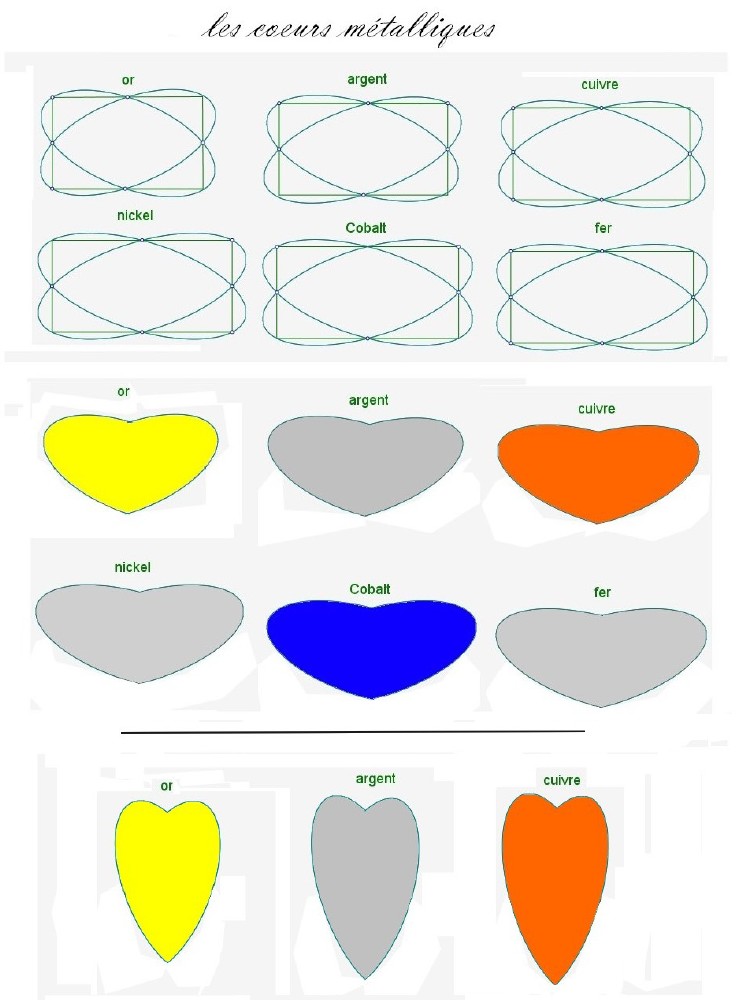
• • 6. LES CŒURS MÉTALLIQUES ........................................................................

Et pour finir, un peu d’amour dans les mathématiques avec cette série de cœurs métalliques :)

– Un grand merci à Dominique Tournès, directeur de l’Irem de la Réunion de 2000 à 2020, qui m’a mis sur la piste des nombres métalliques et m’a soutenu dans mes recherches.
– Un grand merci à mon fils Antonin Bourdin qui m’a mis sur la piste de la limite des nombres métalliques.
– Un grand merci à mon fils Félicien Bourdin qui m’a aidé à peaufiner une démonstration pour prouver que le rectangle d’argent est uniquement constitué de carrés et de rectangles d’argent.
– Un grand merci à Alain Busser pour l’aide sur le logiciel car métal.