Well, mountain lions found me there,
And set me on a eagles wing
He took me past to the outskirts of infinity,
And when he brought me back,
He gave me a venus witch’s ring
(Jimi Hendrix, « Voodoo child »)
Lorsqu’aucun courant ne circule dans un ohmmètre, c’est que la résistance mesurée est infinie ; une échelle homographique (celle de la fonction « inverse ») permet donc de représenter l’infini :
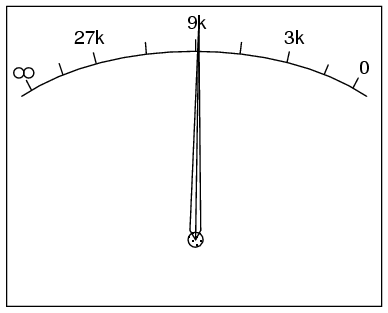
Il y a essentiellement deux manières de traiter l’infini « algorithmiquement » : Le calcul formel, qui considère l’infini comme un symbole sur lequel on peut effectuer des calculs, et le calcul numérique, qui considère l’infini comme un nombre spécial ayant des propriétés spéciales.
JavaScript
En JavaScript, les nombres réels (« float ») sont compris, à cause des limitations de l’ordinateur, entre -1,7976931348623157 × 10308 et 1,7976931348623157 × 10308. Tout nombre inférieur à -1,7976931348623157 × 10308 est donc considéré comme infini négatif, et tout nombre supérieur à 1,7976931348623157 × 10308 est considéré comme infini positif. C’est aussi simple que cela, et surprenamment, ça permet de résoudre pas mal d’exercices sur les limites, parce que l’infini de JavaScript est considéré comme un réel, et les fonctions sur les réels sont parfois définies en ce « nombre ».
Cela permet de boucler de manière raisonnable jusqu’à l’infini (avec CaRMetal) :
for(x=1;x<Infinity;x=Math.pow(2,x)){
Println(x);
}Certes, si on ajoute 1 à tout nombre « trop grand pour la machine », on a encore un nombre « trop grand » :

Ce résultat peut s’interpréter en terme de limite : La limite de x+1 en l’infini est infinie.
De même manière, la limite d’une suite géométrique de raison 2 est infinie :
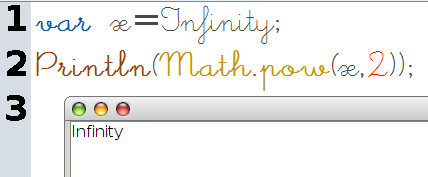
Et la limite de la fonction x3+2x2+3 est aussi infinie :

Plus généralement, JavaScript permet de trouver des limites sans formes indéterminées, comme les « sommes de fonctions de référence » du programme de STI2D. Par exemple, les limites de l’exponentielle, du logarithme :
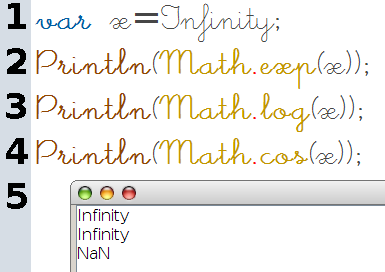
L’abréviation « NaN » de « not a number » montre ici l’absence de limite de la fonction cosinus, mais on a le même affichage avec les formes indéterminées (voir plus bas).
L’inverse d’un nombre trop grand pour être géré par JavaScript, est trop petit pour être distingué de 0 :
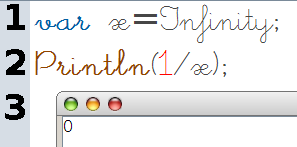
Autrement dit, l’inverse d’un infiniment grand est un infiniment petit...
À l’inverse (!), une division par zéro ne mène pas JavaScript au plantage assuré, mais donne un résultat cohérent avec l’idée que les élèves en cours de formation se font de l’infini :
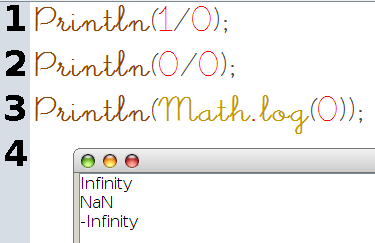
Par contre, le quotient de 0 par 0 ne donne pas l’infini, mais une forme indéterminée (affichée par le « NaN » qui plus haut donnait l’absence de limite identifiable par JavaScript). Pour finir avec l’exemple ci-dessus, la limite de la fonction logarithme en 0 est connue de JavaScript.
L’exemple suivant montre comment les formes indéterminées quotient et produit sont gérées par JavaScript, ainsi que la limite de l’exponentielle en moins l’infini :
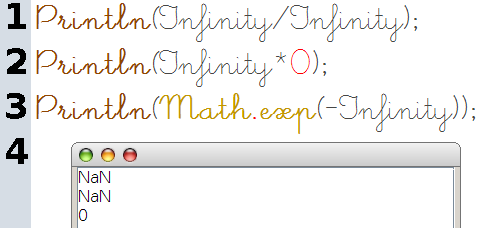
En résumé, la définition de l’infini comme « nombre trop grand » est cohérente avec les propriétés attendues des limites, est statique (image de l’infini par la fonction, plutôt que limite lorsque x tend vers l’infini, et ne gère pas correctement les formes indéterminées. Pour ce dernier cas, il faut un CAS (ou calcul formel), comme on le voit dans les onglets suivants.
GeoGebra
Le calcul formel de GeoGebra [1] effectue un véritable calcul sur les limites, avec l’expression « Limite », suivie de trois arguments :
- l’expression (ou fonction) dont on veut la limite ;
- la variable qui tend vers une limite ;
- la limite vers laquelle tend la variable.
Les exemples de l’onglet précédent s’affichent alors ainsi :

On constate que l’affichage du symbole « infini » est meilleur que le mot « Infinity » de JavaScript, et que, au lieu de dire que la fonction cosinus n’a pas de limite, GeoGebra [2] refuse purement et simplement d’effectuer le calcul.
La calcul formel gère bien mieux que JavaScript, la notion de forme indéterminée :

Cela est dû à ce que le calcul est effectué de façon symbolique plutôt que par divination de l’ordre de grandeur à la JavaScript (si on soustrait un « trop grand nombre » à un autre, on s’attend pas vraiment à trouver quelque chose de prédictible).
Ce calcul symbolique est fait avec des algorithmes du genre
- S’il n’y a pas de forme indéterminée, utiliser les formules de base (par exemple, la somme d’une fonction tendant vers une limite finie et d’une fonction tendant vers l’infini, tend vers l’infini) ;
- La limite d’un polynôme est celle de son terme dominant (de plus haut degré) ;
- La limite d’une fraction rationnelle est celle du quotient des termes dominants du numérateur et du dénominateur.
- et d’autres faits analogues s’il y a des exponentielles ou logarithmes...
Maxima
Le premier logiciel de ce comparatif à gérer les limites était MACSYMA dont l’algorithme de calcul de limite, basé sur la règle de l’Hôpital, est encore utilisé dans son descendant Maxima. Voici l’algorithme [3] :
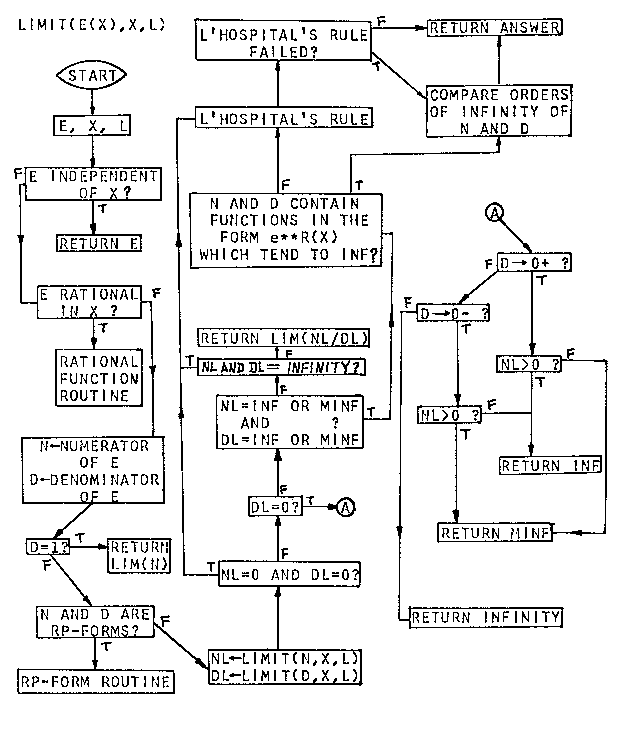
Sur les exemples des onglets précédents, on obtient ceci :

On constate la possibilité de distinguer les limites à gauche et à droite, et l’affichage de la limite de la fonction cosinus comme « indéterminée » ce qui est plus cohérent qu’avec les autres outils vus ici.
Les formes indéterminées sont bien entendu parfaitement gérées :

Les limites sont assez faciles à entrer dans WxMaxima grâce aux fenêtres modales à remplir.
Xcas
Xcas lui aussi, comme tout logiciel de calcul formel, sait calculer des limites :

On constate que la limite de la fonction cosinus est moins lisible qu’avec Maxima, seule la réponse « bounded function » étant fournie.
(entrer ces instructions est plus facile qu’il n’y paraît, grâce au clavier virtuel d’Xcas, sur lequel il suffit de cliquer sur « oo » pour avoir « Infinity »)
Les formes indéterminées sont bien entendu parfaitement gérées :

Géométrie dynamique
Un jour de 2001, un étudiant autrichien, Markus Hohenwarter, s’est dit « tiens, si j’inventais un logiciel qui gère l’infini, à l’aide de la géométrie projective ? ». Il l’a inventé, ce logiciel, lors de son projet de thèse, et l’a nommé GeoGebra. La consultation du code source de ce logiciel révèle les faits suivants :
- Les coordonnées d’un point du plan ne sont pas au nombre de deux mais trois, en ajoutant une coordonnée z égale à 1 (coordonnées homogènes) ;
- La dualité permet d’associer une droite, d’équation ax+by=c, à un point du plan projectif, de coordonnées (a,b,c) ;
- Les formules de Cramer se résument à ce que l’intersection des droites ax+by=c et a’x+b’y=c’ est le point dont les coordonnées homogènes sont obtenues par produit vectoriel entre les vecteurs de coordonnées (a,b,c) et (a’,b’,c’) (déterminants) [4] ;
- Si la troisième coordonnée homogène est nulle, c’est que le point est à l’infini : Les droites sont parallèles.
Ceci permet de simplifier énormément le code source de GeoGebra, la détection des cas particuliers n’étant plus nécessaire.
L’idée de rajouter un point à l’infini à une droite, pour en faire une droite projective, est similaire au comportement de JavaScript lorsqu’on entre (1/0) pour avoir Infinity : le point de la droite dont les coordonnées homogènes sont (1,0) est bien à l’infini.
Quand à DrGeoII, il utilise la notion d’abscisse d’un point sur une courbe, toujours compris entre -0,5 et 0,5, et qui, dans le cas d’une droite, donne un point à l’infini si l’abscisse est -0,5 ou 0,5 :
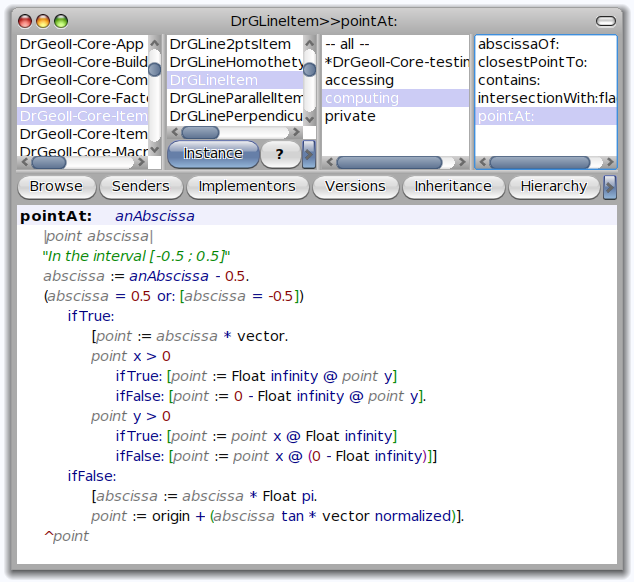
On remarque l’utilisation de la fonction tangente pour que l’abscisse (non linéaire) d’un point soit continue en l’infini (tende vers l’infini si x tend vers -0,5 ou 0,5).
La fonction arctangente permet en effet de tasser les graduations sur un segment, de telle manière qu’on puisse y caser l’infini :
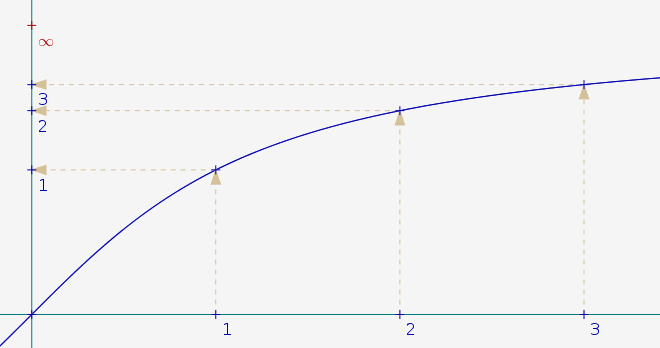
Cela est basé sur le fait que Smalltalk gère l’infini exactement de la même manière que JavaScript [5] avec NaN en cas de forme indéterminée.
Clark
Le nomogramme circulaire de Clark est basé sur la projection stéréographique. La projection stéréographique d’une droite graduée sur un cercle, permet
- de graduer celui-ci ;
- de rajouter l’infini à ces graduations (mais un seul infini, à la fois positif et négatif).
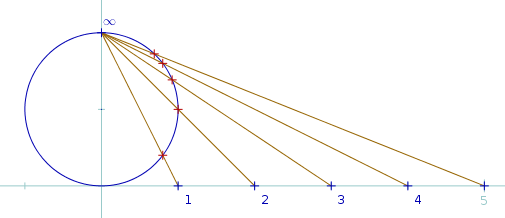
Les graduations sont en effet de plus en plus tassées vers le haut, ce qui laisse de la place pour caser l’infini :

Le nomogramme circulaire de Clark se fabrique en projetant stéréographiquement une demi-droite sur un demi-cercle bleu, une autre demi-droite sur un demi-cercle vert, et un diamètre rouge homographiquement gradué :
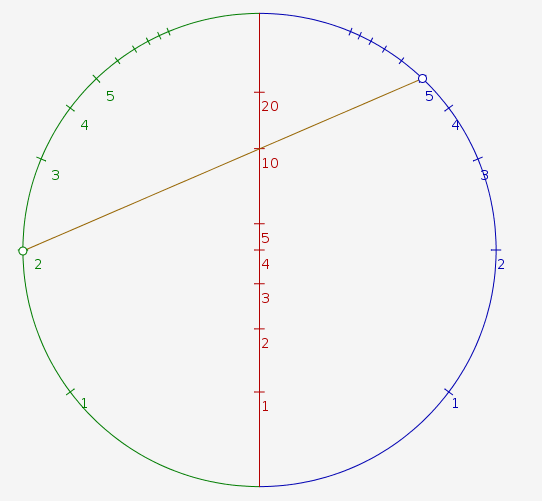
Ci-dessus, on voit comment ce nomogramme peut être utilisé pour multiplier 2 (en vert) par 5 (en bleu) : On joint le 2 vert et le 5 bleu par un segment marron, lequel coupe le diamètre rouge en la graduation 10 (produit de 2 par 5).
Le nomogramme circulaire permet de visualiser le fait que 0 est élément absorbant (« 0 fois n’importe quel nombre, fait 0 ») : En joignant le 0 vert et un nombre bleu, le segment coupe le diamètre rouge en 0, parce que les 0 vert, bleu et rouge coïncident (le produit de 0 par 3 ci-dessous) :

Maintenant, par passage à l’inverse (matérialisé par une symétrie axiale sur le nomogramme circulaire), et parce que les infinis vert, bleu et rouge coïncident également, on « voit » que « le produit de l’infini par un nombre positif est infini » (ci-dessous, le produit de l’infini par 3) :

En effet, si on joint le 3 bleu à l’infini vert, le segment obtenu coupe le diamètre en l’infini puisque ces trois infinis coïncident. De même, « le produit de l’infini par lui-même est infini ».
Enfin, on voit une forme indéterminée : En joignant l’infini vert au 0 bleu, le segment marron coïncide avec le diamètre rouge, et coupe donc celui-ci partout à la fois : Forme indéterminée :

Remarque : Le nomogramme circulaire de Clark permet aussi de voir l’impossibilité de diviser par 0...





Commentaires