En revisitant cet article Initiation à l’algorithmique avec Scratch et Algobox, Exemples de base, écrit en septembre 2009, je souhaite montrer aux élèves comment mettre l’accent sur la notion universelle de fonction en mathématiques. J’ai donc distribué un devoir d’algorithmique à mes élèves de première S et première STMG. Ce devoir présente des algorithmes de base illustrant les notions essentielles d’algorithmique que les élèves rencontreront en mathématiques au cours de leurs années lycée.
 [1]
Depuis cette rentrée scolaire 2018-2019, j’essaye de montrer aux élèves dans la mesure du possible à quel point la compréhension des algorithmes peut les aider dans leur compréhension des mathématiques. J’aborde toute chose sous l’angle des fonctions (voir cet article : « Tout est algorithme, tout est fonction » [2]). En expliquant simplement qu’une fonction, c’est une boîte dans laquelle on entre des objets (nombres, listes d’objets...), et de laquelle ne ressort qu’un unique résultat.

Le devoir d’algorithmique consistait à réécrire les algorithmes d’un devoir d’algorithmique préparé avec le logiciel AlgoBox dans Snap! [3], devoir originel que vous trouverez dans le Port-Folio au bas de cet article.
Il s’agissait ensuite de transformer chaque algorithme en fonction, cela en créant le bloc correspondant dans le logiciel Snap!. Les élèves devaient également écrire un petit commentaire expliquant l’objet de chaque algorithme.
19 algorithmes au total étaient à réécrire sous forme de fonction. [4]

L’utilisation de Snap! permet bien sûr d’assurer la transition entre Scratch que les élèves ont étudié au collège et le langage Python qui est demandé au lycée depuis la rentrée dernière. Mais l’utilisation de Snap! permet bien plus que cela. Il permet d’asseoir la notion de fonction (tant en mathématiques, qu’en informatique) dans l’esprit des élèves.
L’écriture des fonctions en langage Python en devient plus immédiat, plus limpide. Et les élèves, avec leur calculatrice NumWorks [5] écriront à la rentrée [6] les fonctions du devoir en Python.

Ce passage des algorithmes aux fonctions, que ce soit avec Snap! ou avec Python, permet d’épurer chaque algorithme, d’orienter les élèves vers l’essentiel, de ne pas les perdre notamment dans des gestions d’entrées-sorties...

Algorithmique : Les instructions élémentaires

– Déclaration des variables
La plupart des langages de programmation nécessite une phase de déclaration des variables, donc il serait bien d’énumérer avec les élèves la liste des variables dont ils peuvent avoir besoin dans un algorithme.
Voici quelques types de données que les élèves pourront rencontrer :

1. 1. la variable est du type Nombre
   2. la variable est du type Chaîne de caractères
   3. la variable est du type liste de (nombres/chaînes de caractères)
   4. la variable est du type booléen (un booléen ne prend que 2 valeurs : vrai ou faux)

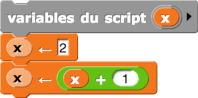
– Affectation
Il s’agit de faire comprendre aux élèves qu’une variable, c’est comme le tiroir d’une commode. Ce tiroir comporte une étiquette (le nom de la variable) ; on y range des objets : le contenu de la variable (par exemple un nombre, une liste de nombres).
Afin de donner aux élèves de bonnes habitudes, ce serait bien de leur faire initialiser leurs variables systématiquement.
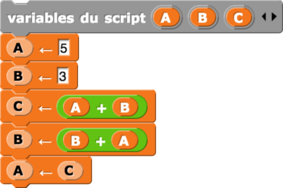
Ce petit algorithme permet d’échanger le contenu des variables a et b.

a ← 2
b ← 3
c ← a
a ← b
b ← c

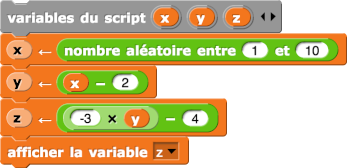
– Calcul
Des calculs sont effectués à partir des variables d’entrée, comme par exemple :

a ← 2
b ← 3
a ← a + b
b ← a - b
a ← a - b

– Entrées / Sorties
Si les variables n’ont pas été initialisées dans l’algorithme, on pourra les lire au clavier par exemple. Une variable doit être affichée pour en connaître le contenu.

Lire a
Lire b
a ← a + b
b ← a - b
a ← a - b
Afficher a, b

Blocs de contrôle : Boucle et itérateur, instruction conditionnelle

– Calcul itératif Pour ... De ... A ...

Lorsque le nombre de boucles est connu, il s’agit d’effecteur un calcul itératif.

 n ← 100
Pour i allant de 1 à n
    action1
    action2
     ...
Fin Pour

Les actions sont effectuées ici 100 fois, le compteur i étant incrémenté (i ← i + 1) à chaque exécution de la boucle.

– Instruction conditionnelle Si ... Alors ... ( Sinon ... )

Si une condition a une valeur logique vraie, on effectue une ou plusieurs actions.

Si condition vraie Alors action1 action2 ... FinSi	Si condition vraie Alors action1 action2 ... Sinon action1b action2b ... FinSi

– Calcul itératif avec fin de boucle conditionnelle Tant Que ... Faire ... ou Faire ... Jusqu’à ...

Le calcul itératif va être exécuté tant qu’une condition a une valeur logique vraie ou le calcul itératif va être arrêté lorsque la condition a une valeur logique vraie.

Tant Que condition vraie Faire
    action1
    action2
    ...
Fin Tant Que

Répéter
    action1
    action2
    ...
Jusqu'à condition vraie
Fin Répéter

Devoir d’algorithmique

En classe, depuis cette année, j’écris tous mes algorithmes avec Snap!.
En effet, j’ai pu créer mes propres blocs Snap! [7] spécifiques à l’écriture des algorithmes (ils sont donnés au bas de cet article), de sorte à obtenir mon propre IDE [8] idéal à l’enseignement de l’algorithmique en classe. Une bibliothèque spécifique à l’écriture des algorithmes en français sera prochainement intégrée aux librairies additionnelles de Snap!.

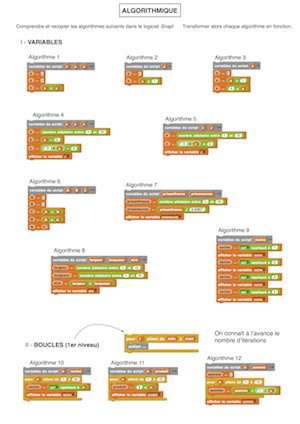
Voici le devoir entièrement réécrit avec Snap! :

Devoir d’algorithmique, page 1	Devoir d’algorithmique, page 2

– Variables

9 algorithmes sont proposés dans le devoir pour illustrer la notion de variables.

Algorithme 1

L’algorithme proposé	fonction correspondante
algorithme 1	fonction 1
appel à la fonction

Code Python	appel à la fonction
def algo1(x,y): return x+y	algo1(2,3)

Déplier tous les blocs
Replier tous les blocs

Algorithme 2

L’algorithme proposé	fonction correspondante
algorithme 2	fonction 2
appel à la fonction

Code Python	appel à la fonction
def algo2(x): return x+1	algo2(2)

Algorithme 3

L’algorithme proposé	fonction correspondante
algorithme 3	fonction 3
appel à la fonction

Code Python	appel à la fonction
def algo3(x): return 4*(x+1)	algo3(2)

Algorithme 4

L’algorithme proposé	fonction correspondante
algorithme 4	fonction 4
appel à la fonction

Code Python	appel à la fonction
def algo4(x): return -3*(x-2)-4	from random import randint algo4(randint(1,10))

Algorithme 5

L’algorithme proposé	fonction correspondante
algorithme 5	fonction 5
appel à la fonction

Code Python	appel à la fonction
def algo5(x): return -3*x+2	from random import randint algo5(randint(1,10)) ce qui donne dans un terminal : Quel a été le nombre tiré au hasard ?

Algorithme 6

L’algorithme proposé	fonction correspondante
algorithme 6	fonction 6
	variante efficace
appel à la fonction

Code Python	appel à la fonction	définition d’une fonction Python épurée...
def algo6(A,B): return [A+B,B+A]	algo6(5,3)	def algo6(A,B): return [A+B,A+B]

Remarque importante : Cet algorithme est l’occasion d’insister sur l’ordre des instructions dans un algorithme. [9]

Algorithme 7

L’algorithme proposé	fonction correspondante
algorithme 7	fonction 7

appel à la fonction

Code Python	appel à la fonction
def algo7(prixenfrancs): return prixenfrancs/6.55957	algo7(100)

Algorithme 8

L’algorithme proposé	fonction correspondante
algorithme 8	fonction 8
appel à la fonction

Code Python	appel à la fonction
def algo8(largeur,longueur): return largeur*longueur	algo8(20,30)

Algorithme 9

L’algorithme proposé	fonction correspondante
algorithme 9	fonction 9
	Le script de la fonction algo9
appel à la fonction

On peut alors appliquer l’algorithme 9 - qui n’est autre que la fonction racine carré - aux nombres d’une liste

Code Python	appel à la fonction
from math import sqrt def algo9(x): return sqrt(x)	algo9(2) liste = [1,2,3,4] map(algo9, liste) ce qui donne dans le terminal :

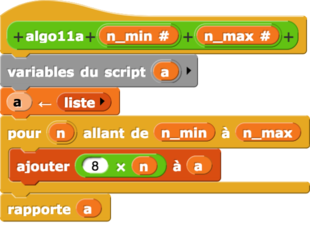
– Boucles de niveau I

3 algorithmes sont donnés dans le devoir pour illustrer la notion de boucles dont le nombre d’itérations est connu à l’avance.

Algorithme 10

L’algorithme proposé	fonction correspondante
algorithme 10	fonction 10

variante efficace

appel à la fonction

Code Python	appel à la fonction
from math import sqrt def algo10(n_min,n_max): a = [] for n in range(n_min,n_max): a.append(sqrt(n)) return a	algo10(1,50)

Algorithme 11

L’algorithme proposé	fonction correspondante
algorithme 11	fonction 11

variante efficace

appel à la fonction

Code Python	appel à la fonction
def algo11(n_min,n_max): a = [] for n in range(n_min,n_max): a.append(8*n) return a	algo11(1,10)

Algorithme 12

L’algorithme proposé	fonction correspondante
algorithme 12	fonction 12

appel à la fonction

Cette somme des inverses des entiers naturels de 1 à 10 peut se calculer très simplement avec la combinaison des 2 fonctions Appliquer/Combiner (map/reduce)

et une variante efficace pour la fonction 12 se trouve donc être

Code Python	appel à la fonction
def algo12(n_min,n_max): somme = 0 for n in range(n_min,n_max): somme = somme +1./n return somme	algo12(1,10)

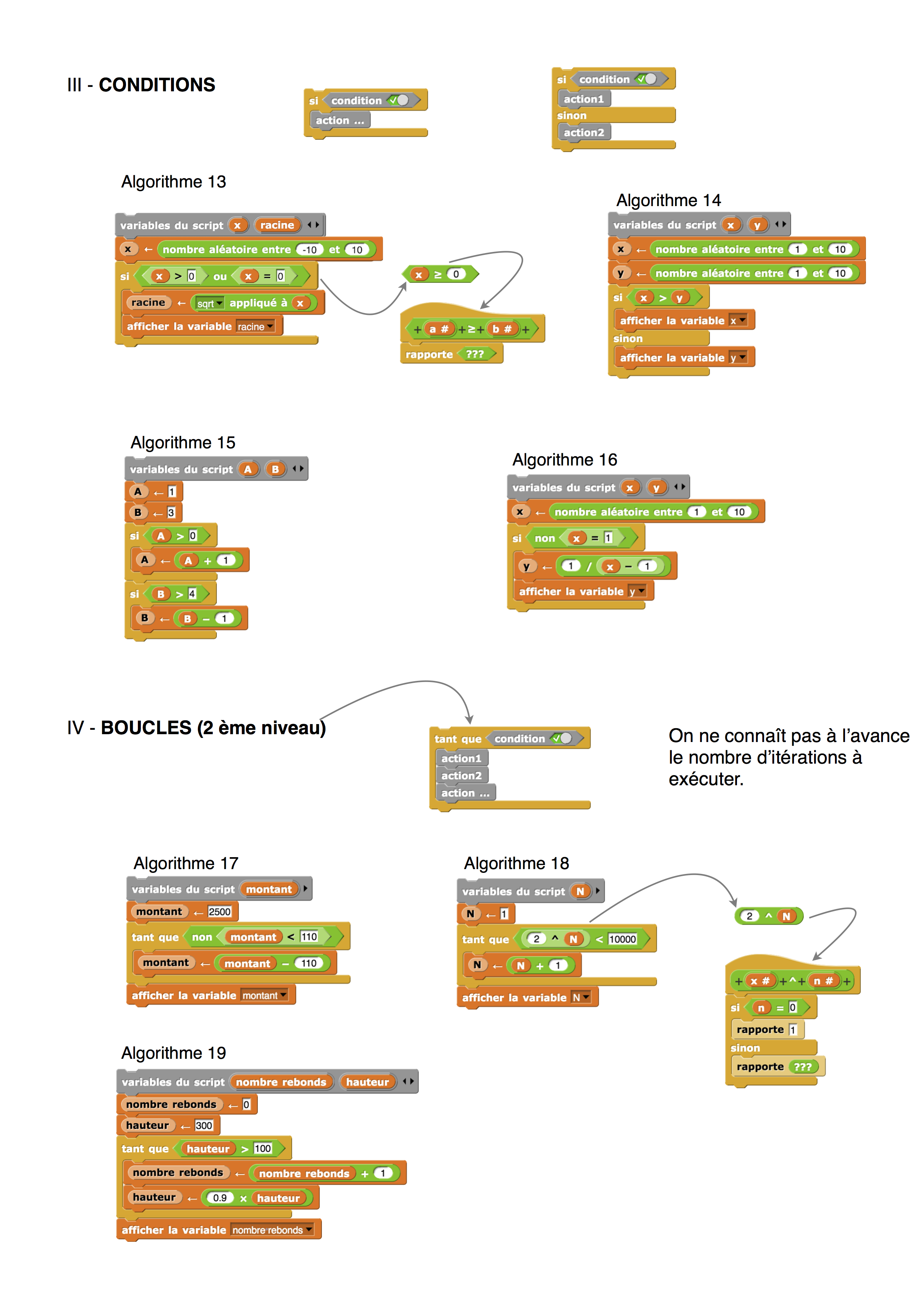
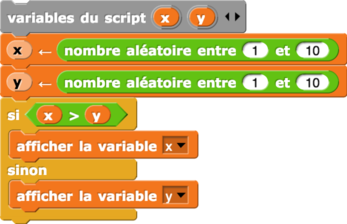
– Conditions

4 algorithmes illustrent la notion d’instructions conditionnelles.

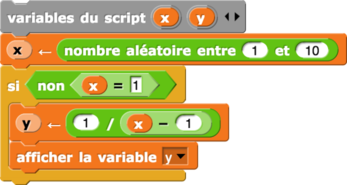
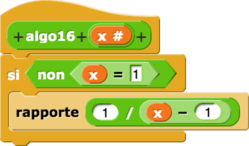
Algorithme 13

L’algorithme proposé	fonction correspondante
algorithme 13	fonction 13

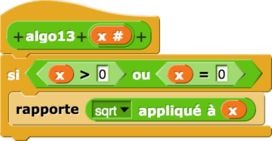
Ce qui donne l’occasion de programmer un booléen

appel à la fonction

Code Python	appel à la fonction
from math import sqrt def algo13(x): if (x > 0 or x == 0): return sqrt(x)	algo13(3)

 [10]

Algorithme 14

L’algorithme proposé	fonction correspondante
algorithme 14	fonction 14
appel à la fonction

Code Python	appel à la fonction
def algo14(x,y): if x > y: return x else: return y	from random import randint algo14(randint(1,10),3)

Algorithme 15

L’algorithme proposé	fonction correspondante
algorithme 15	fonction 15
appel à la fonction

Code Python	appel à la fonction
def algo15(A,B): if A > 0: A = A + 1 if B > 4: B = B - 1 return [A,B]	algo15(1,3)

Algorithme 16

L’algorithme proposé	fonction correspondante
algorithme 16	fonction 16
appel à la fonction

Code Python	appel à la fonction
def algo16(x): if !(x==1): return 1/(x-1)	from random import randint algo16(randint(1,10))

 [11]

– Boucles de niveau II

3 algorithmes sont donnés dans le devoir pour illustrer la notion de boucles qui seront exécutées à l’aide de la réalisation d’une certaine condition.

Algorithme 17

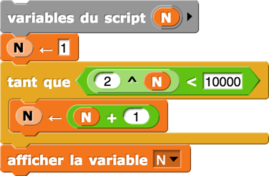
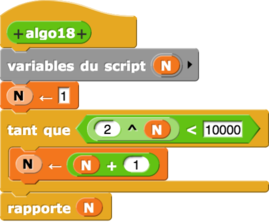
L’algorithme proposé	fonction correspondante
algorithme 17	fonction 17
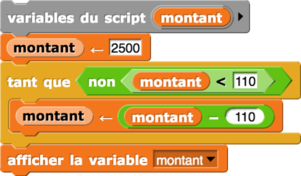
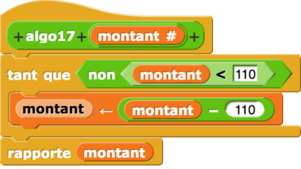
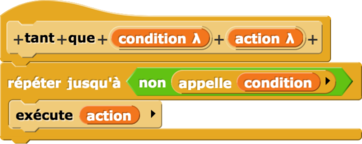
La condition peut évidemment s’écrire :	ou
appel à la fonction
>	2500-22*110 = 80

Code Python	appel à la fonction
def algo17(montant): while montant >= 110: montant = montant-110 return montant	# le montant doit être supérieur ou égal à 110 # afin que la boucle soit exécutée au moins une fois. algo17(2500)

Algorithme 18

L’algorithme proposé	fonction correspondante
algorithme 18	fonction 18
appel à la fonction
Cette fonction renvoie le premier entier naturel N à partir duquel 2^N ≥ 10 000

Vérification

Code Python	appel à la fonction
def algo18(): N = 1 while 2**N < 10000: N = N + 1 return N	# algo18()

Tiens ! Une fonction sans entrée(s). On peut alors décider de paramétrer le nombre 10000 à l’aide d’un passage par argument de cette valeur et de placer le nombre 10000 dans un tiroir qui s’appellera nombre par exemple.

Code Python	appel à la fonction
def algo18(nombre): N = 1 while 2**N < nombre: N = N + 1 return N	# on passe alors le nombre 10000 en argument à la fonction. algo18(10000) # La fonction renvoie 14 # (le premier entier naturel N à partir duquel 2^N ≥ 10 000) # ce qui permet de relancer l'appel à la fonction # avec une nouvelle valeur si besoin : algo18(500000) # La fonction renvoie maintenant 19 # (le premier entier naturel N à partir duquel 2^N ≥ 500 000)

Algorithme 19

L’algorithme proposé	fonction correspondante
algorithme 19	fonction 19
on peut aussi envisager un retour plus détaillé de la fonction
appel à la fonction
Cette fonction renvoie le nombre de rebonds nécessaires à la balle pour passer en dessous de la hauteur 100.

Code Python	appel à la fonction
def algo19(hauteur): nombre_rebonds = 0 while hauteur > 100: nombre_rebonds = nombre_rebonds + 1 hauteur = 0.9 * hauteur return nombre_rebonds	algo19(300) # la fonction algo19 renvoie # le nombre de rebonds nécessaires # à la balle # pour passer de la hauteur initiale # de 300 # en dessous de la hauteur 100.

Blocs spécifiques Snap! pour écrire les algorithmes demandés

– Script pour la flèche d’affectation

La boucle Pour i allant (...)

La boucle Pour i allant de 1 à n
On la trouve dans la librairie Tools à précharger avant Snap! 5, et est intégrée par défaut à Snap! 5.

...et son programme Snap!

La boucle Tant que

un programme Snap! pour la boucle Tant que

On utilise la boucle Répéter ... Jusqu’à ... déjà présente par défaut dans les blocs de contrôle pour créer ce bloc.

Définition récursive de la fonction puissance

une fonction qui renvoie un booléen

Les fonctions : corrigé du devoir d’algorithmique

Vous trouverez la totalité des blocs présentés dans cet article sur le cloud de Snap! Berkeley.
https://snap.berkeley.edu/snapsource/snap.html#present:Username=nathalierun&ProjectName=2018-12-27-Algorithmique.Solution

5 lutins y sont présents, ils correspondent aux différentes parties du devoir :
– le lutin Variables
– le lutin Boucles1
– le lutin Conditions
– le lutin Boucles2
– le lutin algorithmique

Quelques indications sur le barême que j’ai appliqué à ce devoir numérique :
– 0.5 par script transcris correctement
– 0.5 par fonction correcte
– 0.25 pour toute explication correcte du but de l’algorithme, écrite sous forme de commentaire.
1 point pour la présentation générale des résultats (4 lutins).
Avec 19 algorithmes, cela fait bien un barême sur 20 (le total étant tronqué à 20).
Ce barême garantit quasiment la moyenne pour chaque élève qui a rendu son devoir. Je pratique en général une évaluation positive et essaye toujours d’encourager les élèves qui ont rendu quelque chose, pour avoir au moins essayé. Le devoir était globalement assez difficile, mais il m’a permis de voir si les élèves avaient bien compris les algorithmes écrits et les notions de boîte pour les fonctions. Ils ont dû nécessairement distinguer quelles étaient les entrées données à la boîte, et quel était le résultat qui devait en sortir.

Le devoir était obligatoire en première S ( à rendre avant les vacances de l’été austral ) ; et facultatif en première STMG ( à rendre à la rentrée).
Pour la classe de première S, le coefficient appliqué à ce devoir est 4. Je donne aussi régulièrement des devoirs [Wims] à faire en ligne (coefficient 1), des interrogations surprises coefficient 2, et des devoirs sur table (prévenus) coefficient 4, mais encore des projets à faire à la maison qui demandent un lourd investissement personnel comme un devoir sur la fractale de Von Koch (qui comporte de l’algorithmique, des calculs et des dessins papier). Ce dernier est compté coefficient 4.

Quelques remarques de correction :
Dans les erreurs trouvées dans les copies numériques, les plus intéressantes sont :
– Beaucoup de confusion entre les arguments d’entrée et ceux de sortie. Ainsi, les arguments d’entrée sont x, y, z pour l’algorithme 4, alors que seul x est un argument à entrer dans la fonction, y et z sont issus de calcul et seul z est à retourner.
– une élève a codé « rapporter » au lieu de « afficher » dans le script Snap!
– ceci n’est pas une erreur, bien au contraire. Depuis que les élèves connaissent la fonction Snap! « Appliquer » (« Mapper »), ils ne font plus de boucle... car ils ont bien compris que c’est tellement plus direct, tellement plus efficace !

Se former à Snap!

– On pourra suivre ce MOOC de formation à Snap! sur openSAP.

– S’abonner au compte Twitter de Jens Möenig, le développeur principal de Snap!, vous permettra d’être au courant des principales modifications apportées à Snap!.

– La chaîne Youtube de Jens Möenig présente quelques tutoriaux essentiels pour utiliser Snap!.

 [12]

D’autres articles sont consacrés à Snap! sur ce site, faisant l’apologie des algorithmes et des fonctions :

– Programmer des algorithmes avec Snap! ou la programmation visuelle au lycée
– L’héritage des Micromondes LOGO : programmation fonctionnelle au collège avec Snap!, article qui explique pourquoi passer de Scratch à Snap! pour préparer le brevet en physique chimie au collège.
– Pourquoi faire des fractales en classe ? qui permet de visiter l’algorithmique au travers de la géométrie avec Snap!.
– Rouge, Vert, Bleu, de 0 à 255 pour comprendre le codage des couleurs avec Snap!.
Et enfin cet article de fond [13] :
– Tout est algorithme, tout est fonction qui constitue une première approche d’une pensée fonctionnelle du programme de première scientifique.