Le sujet du TP était, pour une fois, court : Écrire un algorithme qui, à partir de la représentation graphique d’une fonction affine (une droite), donne son coefficient directeur et son ordonnée à l’origine.
Voici le sujet au format pdf :
Difficile de savoir comment le TP se serait déroulé : Il ne s’est pas déroulé, en raison d’un orage sérieux : 3 coupures de courant pendant la première heure, et absence totale de réseau pendant la deuxième heure...
Bilan : Un seul élève du premier groupe a réussi à obtenir le coefficient directeur, et au moment où il allait sauvegarder son travail en cliquant sur l’icône représentant une disquette, la foudre est tombée, provoquant une micro-coupure de courant, tout juste assez longue pour éteindre les ordinateurs... De mémoire son script ressemblait à ceci :
var xM,yM,xN,yN;
xM=X("M");
yM=Y("M");
xN=X("N");
yN=Y("N");
var a=(yM-yN)/(xM-xN);
Alert("le coefficient directeur est "+a);Le coefficient directeur est correct, mais si on bouge les points M et N, il ne le reste pas (il n’est pas actualisé).
Sans JavaScript
Pendant le week-end suivant (lorsque l’orage et les fortes pluies ont cessé), un autre élève a trouvé une autre manière d’implémenter l’algorithme, directement sous CaRMetal : Il a créé une expression a égale à :
(y(M)-y(N))/(x(M)-x(N))et il a créé le point d’intersection P de la droite (MN) et de l’axe des ordonnées, puis dans la variable b, placé
y(P)ce qui était inespéré [1] !
Voici son TP (la seule modification qui y a été apportée est un redimensionnement) :
Comme on le voit, le mouvement des points M et N met à jour les deux coefficients !
Corrigé du TP
Pour éviter d’avoir à écrire b=y(M)-a*x(M), on peut très bien créer le point d’intersection O de la droite d et de l’axe des ordonnées comme l’a fait l’élève dont le travail est publié ci-dessus (il faut juste que la grille soit visible).
Sur une figure comprenant les points M, N et O et la droite d, le script suivant évite le problème des données statiques :
/*Correction du TP 5
Seconde ISI 1
LRG, Le Tampon
Novembre 2009*/
var a,b;//coefficients
a=Expression("(y(M)-y(N))/(x(M)-x(N))",-4,-2);
b=Expression("y(O)",-4,-3);
var m=GetExpressionValue(a);
var p=GetExpressionValue(b);
Alert("le coefficient directeur est "+m);
Alert("l'ordonnée à l'origine est "+p);Le script abuse des entrées-sorties : Il crée deux « expressions » dans le langage de CaRMetal et s’arrange pour qu’elles contiennent le coefficient directeur et l’ordonnée à l’origine. Puis (variables m et p), il récupère les valeurs de ces expressions (des nombres) et les affiche.
Lorsque l’utilisateur a fermé les deux boîtes de dialogue, la figure reste manipulable et les coefficients, affichés sans leurs noms, sont mis à jour.
Comme le montre le fichier de l’élève ci-dessus, il est somme toute plus simple de faire la manip directement sous CaRMetal [2]. On peut d’ailleurs faire encore plus simple avec un peu d’expertise de CaRMetal : L’instruction « x(M) » est décrite comme donnant l’abscisse de l’objet M et M n’est donc pas forcément un point : x(d) retourne un résultat numérique, mais qu’est-ce que l’abscisse d’une droite ? En fait c’est l’abscisse d’un vecteur directeur de la droite. Alors l’expression
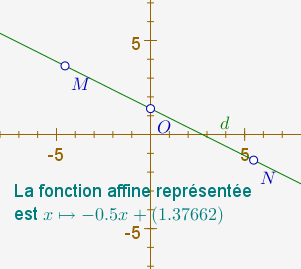
y(d)/x(d)donne le coefficient directeur. Enfin l’usage d’une formule LaTeX [3] permet d’afficher simultanément les deux variables numériques a et b (dès lors que leur nom est en sandwich entre deux symboles « pourcent ») :
La fonction affine représentée
est $x \mapsto %y(d)/x(d)%x+(%y(O)%)$ce qui produit la figure suivante :
Il est d’ailleurs possible de créer une macro « équation réduite » à partir de ce fichier, à condition d’opérer sur deux points A et B liés à d, au lieu des points M et N qui ont servi à définir d.
Conclusions
Avant le déchaînement de Zeus, beaucoup d’élèves semblaient bloqués par la notion d’entrée-sortie, ce qui est surprenant compte-tenu du fait que tous avaient réussi le TP 2. On peut donc estimer que si l’apprentissage des entrées-sorties est très rapide, la notion mérite d’être révisée régulièrement pour pérenniser cet apprentissage.
La manière habituelle pour approfondir le cours sur les fonctions affines est la multiplication d’exercices (voir par exemple la version mathenpoche), ce qui approfondit (assez difficilement d’ailleurs) la connaissance déclarative des élèves sur la question. Ce genre de TP, qui appelle directement leur connaissance procédurale, présente un intérêt nouveau. La version AlgoBox peut être intéressante à tester en classe, même si l’entrée des données est plus pénible avec ce dernier outil. Par contre la programmation sur calculatrice pose problème si on compte autoriser la calculatrice lors du contrôle suivant...

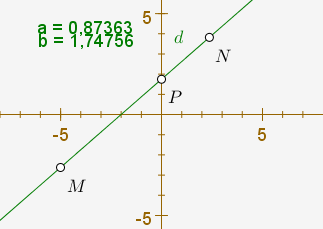
Commentaires