La représentation graphique de $f(x)=x^2e^{1-x^2}$ a été obtenue avec l’outil adéquat, en entrant l’expression
x^2*exp(1-x^2)et les bornes 0 et 1.
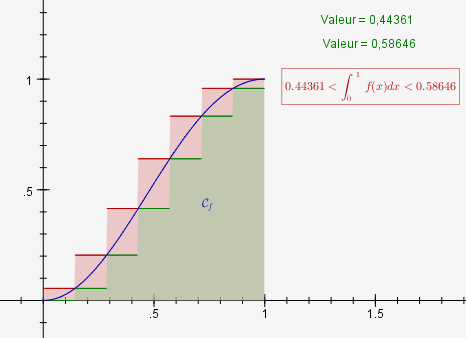
Les fonctions en escalier f2 et f3 ont été rajoutées pour pouvoir calculer leur intégrale. Leurs expressions sont
f(floor(x*N)/N)
f(ceil(x*N)/N)où $N$ est un curseur (en haut à gauche).
Enfin, $S_n$ et $T_n$ sont deux expressions valant
integrate(f2;0;1)
integrate(f3;0;1)
la figure du TP
Il suffit de glisser le curseur de la figure ci-dessus vers la graduation 100 pour finir le TP [1] !
Commentaires