Le problème est posé dans cet article d’un site multi-langages (de programmation). Voici la description qui en est donnée :
Ethiopian multiplication is a method of multiplying integers using only addition, doubling, and halving.
Le problème qui sera traité ici est celui de la sémantique : Que signifient exactement les verbes to double (doubler) et to halve (diviser par 2) ? Aussi surprenant que cela puisse paraître, ces verbes ont des significations différentes pour les uns et les autres, comme on le voit sur les extraits de programmes ci-dessous.
Double(r)
Sur le site rosettacode, la plupart des solutions utilisent une fonction qui calcule le double d’un entier, au lieu d’une instruction qui double un entier. Pourtant, dans le cas de la division par 2, le verbe to halve n’est pas confondable avec la fonction half. En français, il s’agirait de confondre « doubler » avec « le double de » et « diviser par 2 » avec le quotient « la moitié de ». Par exemple la première solution donnée en Python
def halve(x):
return x // 2
def double(x):
return x * 2qui oblige à remplacer le multiplieur et le multiplicande par leur moitié (respectivement double) :
multiplier = halve(multiplier)
multiplicand = double(multiplicand)Python
En fait, en Python, l’instruction « doubler x » ne peut pas être définie comme une fonction, parce que lorsqu’on fait appel à une fonction f(x), la variable x est locale, c’est-à-dire qu’elle n’existe et ne peut être modifiée que dans le corps de la fonction. Par exemple avec ce script :
def doubler(x):
x += x
return x
a = 3
doubler(a)
print(a)Les trois lignes de programme sont en bas : La première a pour effet que a soit égal à 3, et la dernière affiche 3 puisqu’elle affiche a et que a=3. Donc la seconde ligne n’a pas eu d’effet. Pourquoi ? Parce que doubler(a) a eu pour effet d’appeler la fonction f avec 3 dans x. Successivement, il s’est passé ceci :
- la variable x a été créée ;
- Le contenu de a (c’est-à-dire 3) a été copié dans x (à ce stade, x=3) ;
- Le contenu de x (pour l’instant, 3) a été rajouté (+=) à x (« += » voulant dire ’augmenter de", x vaut alors 3+3=6) ;
- Le nombre obtenu (6) est retourné ;
- La variable x ne servant plus à rien est jetée dans la poubelle (« ramasse-miettes »)
Alors a est toujours égal à 3 et x n’existe plus. Bref, raté ! En fait, le problème est que Python est un langage trop évolué et ne sait pas (du moins, simplement) modifier les variables directement dans la mémoire de la machine [1]. Il faut donc, ou bien des langages possédant déjà des instructions du genre « augmenter de » ou « doubler » (exemples typiques : Cobol et Perl 6), ou bien des langages proches de la machine (exemples : C ou l’assembleur). Voici des exemples de ces langages, décortiqués (onglets suivants) :
Cobol
PROGRAM-ID. halve.
DIVIDE n BY 2 GIVING m END-DIVIDE
PROGRAM-ID. twice.
MULTIPLY n by 2 GIVING m END-MULTIPLY
...
IF odd
ADD r TO product GIVING product END-ADD
END-IF
CALL "halve" USING
BY CONTENT l,
BY REFERENCE l
END-CALL
CALL "twice" USING
BY CONTENT r,
BY REFERENCE r
END-CALLVerbeux mais intéressant (on est assez proche de l’anglais naturel, et Cobol date de l’époque où on imaginait qu’un jour on programmerait des ordinateurs à la voix, permettant des choses comme ça).
En bref, Cobol permettant de multiplier ou diviser par 2, on définit des mots « halve » et « twice » à partir de ces instructions. Cobol tombant quelque peu en désuétude, il ne semble pas y avoir eu d’équivalent dans les langages plus modernes, à part les exemples des onglets suivants (et Sofus, pour la version française).
Perl 6
En plus on a la concision puisque voici l’intégralité du code :
sub halve (Int $n is rw) { $n div= 2 }
sub double (Int $n is rw) { $n *= 2 }
sub even (Int $n --> Bool) { $n %% 2 }
sub ethiopic-mult (Int $a is copy, Int $b is copy --> Int) {
my Int $r = 0;
while $a {
even $a or $r += $b;
halve $a;
double $b;
}
return $r;
}Le symbole « dollar » désigne « la valeur de la variable », ce qui fait que $n est le contenu de la variable n ; alors $n div= 2 veut dire que le contenu de n est divisé par 2. Noter que cette abréviation, qui vient de bash, se retrouve aussi dans le très populaire (du moins chez les élèves) php.
Le mot « my » remplace le « local » des autres langages : La variable r initialisée à 0 est intitulée « my r » parce que c’est « mon r à moi tout seul » : C’est une bonne façon de traduire la notion de variable locale. On remarque que l’idée a été reprise dans Scratch, chaque lutin pouvant avoir ses propres variables.
On remarque que le si..alors est développé comme la forme disjonctive d’une implication : Ou bien le contenu de a est pair, ou alors on ajoute le contenu de b à celui de r.
Forth
Forth fonctionne avec une pile, du coup la syntaxe du doublement est très concise : 2/, qui a pour effet de placer 2 sur la pile puis de le remplacer par son produit avec le précédent sur la pile. L’algorithme est donc extrèmement court (tout l’algorithme est présent ici, il n’en manque pas un octet !), comme c’est souvent le cas avec Forth :
: even? ( n -- ? ) 1 and 0= ;
: e* ( x y -- x*y )
dup 0= if nip exit then
over 2* over 2/ recurse
swap even? if nip else + then ;Détaillons la première ligne : On place n sur la pile, puis 1, et on effectue un « and » (qui va remplacer les deux derniers nombres de la pile par leur conjonction bit par bit). Le haut de la pile contient alors n modulo 2 (parce que, en binaire, un « and » avec 1 donne exactement n modulo 2). Ensuite on effectue un test d’égalité avec 0 et on met le résultat en haut de la pile (c’est comme ça que Forth récupère les données, par lecture du haut de la pile).
L’algorithme (fonction « e ») utilise aussi la pile, avec
- dup qui recopie le nombre tout en haut de la pile, au-dessus de lui -même (ce qui constitue une duplication) ;
- swap qui échange le dernier nombre avec l’avant-dernier dans la pile ;
- over qui place une copie de l’avant-dernier nombre de la pile par dessus le dernier (il fait donc comme dup mais recopie l’avant-dernier nombre au lieu du dernier)
- et nip, qui supprime l’avant-dernier nombre de la pile.
Qui dit « pile », dit notation polonaise inversée, donc a priori, utiliser Forth (langage) (qui a été créé pour de l’électronique embarquée, en l’occurence du pilotage de téléscope)) au collège, n’est peut-être pas une bonne idée (euphémisme)...
Fortran
C’est probablement à cause de son âge que Fortran n’est pas muni des barrières qui empêchent de toucher à ses variables :
subroutine halve(v)
integer, intent(inout) :: v
v = int(v / 2)
end subroutine halve
subroutine doublit(v)
integer, intent(inout) :: v
v = v * 2
end subroutine doublit
...
call halve(plier)
call doublit(plicand)Par contre le doublement est obtenu avec v = v * 2 qui a laissé perplexe pas mal de monde depuis la création du langage vers le milieu des années 1950 (c’est un peu en réaction par rapport à cette notation qu’ont été créés, à la fin des années 1950, Algol et Cobol)...
C
pour modifier une variable in situ, le langage C utilise un pointeur (programmation), représenté par une étoile après le nom de la variable. Pour multiplier un nombre par 10, en décimal, il suffit de le décaler d’un chiffre vers la gauche et insérer un 0 à droite. En binaire, cette opération a pour effet de doubler le nombre. Le décalage est noté >>1 si on décale d’un seul chiffre binaire, et le décalage en place (le doublement, quoi) se note >>=1 :
void halve(int *x) { *x >>= 1; }
void doublit(int *x) { *x <<= 1; }
...
halve(&plier); doublit(&plicand);Par contre C n’est ni concis ni naturel, et même si on trouve régulièrement des programmeurs en C qui arrivent en Seconde avec une certaine maîtrise du langage (et qui donc l’ont (auto-)appris au collège), ils ne sont pas majoritaires en nombre...
bash
Le langage bash est, lui aussi, proche de la machine, ce qui là aussi permet de définir des instructions (ou « commandes ») de doublement etc ; là aussi le code est concis, et reprend certaines des idées précédentes :
halve() {
(( $1 >>= 1 ))
}
double() {
(( $1 <<= 1 ))
}
is_even() {
(( ($1 & 1) == 0 ))
}
multiply() {
local plier=$1
local plicand=$2
local result=0
while (( plier > 0 ))
do
is_even plier || (( result += plicand ))
halve plier
double plicand
done
echo $result
}En bash, le symbole $1 représente le premier argument (ou le seul s’il n’y en a qu’un). Donc doubler $1 c’est le décaler d’un chiffre binaire vers la gauche (en ajoutant automatiquement un 0 comme nouveau dernier chiffre). Le diviser (« halve ») par deux c’est le décaler dans l’autre sens (vers la droite, en perdant l’ancien dernier chiffre).
Pour le test de parité, un « et » est effectué, chiffre par chiffre, entre le nombre à tester et le nombre 1 : Tous les chiifres binaires de 1, sauf le dernier, sont nuls, et 0 est élément absorbant pour la conjonction. Donc $1&1 ne laisse que le dernier chiffre de $1, soit 0 ou 1 selon que $1 est pair ou impair.
On remarque que l’évaluation paresseuse des disjonctions est utilisée ici : si le multiplieur (« plier ») est pair alors la disjonction est vraie et il n’est plus nécessaire d’évaluer son second terme. Mais si le multiplieur est impair alors la disjonction a la même valeur de vérité que son second terme qui est alors calculé : Bref, on augmente « result » de « plicand » seulement lorsque « plier » est impair. Voir à l’onglet « perl 6 » pour une façon plus naturelle d’exprimer ce principe.
assembleur
Même principe : Pour doubler, on décale (« shift to the left » abrégé en shl) d’un bit vers la gauche, et pour diviser par 2, on décale vers la droite (« shift to the right » abrégé en shr). On a choisi de faire ces opérations sur le registre ebx :
halve
shr ebx, 1
ret
double
shl ebx, 1
retLe nom de « EBX » désigne la version étendue (« E » ; parce que 32 bits c’est plus étendu que 16 bits) du registre « BX » du 8086 ; « BX » parce que c’est le registre de base (« B »). Les registres principaux du processeur 80386 sont les suivants :
- EAX est l’accumulateur qui est fait pour des choses comme « augmenter de » : Il écrase son ancien contenu par la somme (on s’en sert surtout pour additionner beaucoup de nombres, ce qui fait qu’il accumule les nombres en sommes partielles, d’où son nom) ;
- EBX est donc le registre de base, celui dont on se sert quand on n’en utilise pas d’autres ;
- ECX est le registre compteur, il a un fonctionnement similaire à celui de l’accumulateur mais spécialisé dans les incrémentations constantes (de 1 si on utilise les octets, d’une puissance de 2 dans le cas général) ;
- EDX est le registre de données qui est utilisé pour les échanges avec la mémoire de l’ordinateur.
On a vu plus haut que Cobol permet de doubler (avec « multiply n by 2 ») et de diviser par 2 (avec « divide n by 2 »). Sofus fait en quelque sorte mieux, puisque le verbe « doubler » fait partie du vocabulaire de base de Sofus. Voici donc la solution du problème de rosettacode avec Sofus :
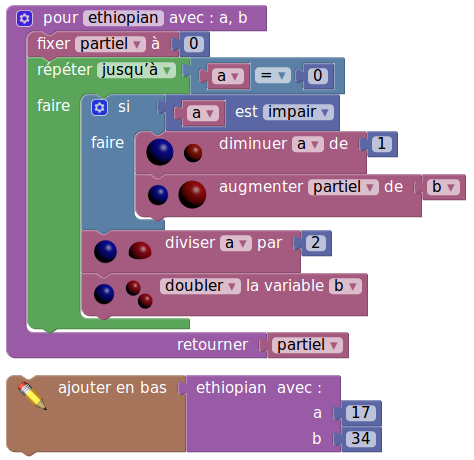
C’est si beau qu’on se prend à rêver que le très obligatoire Scratch (langage) comprenne aussi des instructions comme « doubler » ou « diviser par 2 ». Cela semble tout-à-fait possible, puisque Scratch contient déjà un héritage de Cobol : L’instruction « incrémenter de », dont la fantastique (mais vraie) histoire est narrée [2] ci-dessous :
Scratch 1.4
Au commencement était Mitch Resnick, qui, au milieu d’un chaos cobolien, conçut l’idée de programmer par blocs. Il programma Scratch pendant des mois, avec son équipe du MIT, puis, fatigué par les efforts de programmation (en Smalltalk tout de même), par distraction, il commit l’impensable :
Il ajouta un bloc à la Cobol dans Scratch
Si si, ce bloc, le voici dans toute la splendeur de Scratch 1.4 en anglais (« incrémenter » ayant été traduit par « change » soit « modifier ») :

La traduction littérale étant « modifier n de 1 », on a bien là une instruction de modification sofusienne in situ...
La fatigue de Mitch Resnick lui a fait oublier, soit de créer d’autres instructions similaires (« multiplier par » etc) soit d’enlever cette étrange instruction étrangère. Mais les traductions de « change by » sont un peu surprenantes (voir les autres onglets) :
En français
Dans la traduction française de Scratch 1.4, le bloc sofusien vu précédemment s’est traduit ainsi :

Il s’agit d’une traduction littérale :
- « change » est devenu « changer » (« modifier » ou « incrémenter » eût été plus judicieux)
- « by » est devenu « par » au lieu de « de »...
Mais le pire reste à venir (onglets suivants, sauf le prochain qui est une pause)...
Au Québec
C’est au Québec, probablement sous l’influence de Pierre Couillard, qu’une nouvelle traduction, prenant mieux en compte ce bloc d’incrémentation, est venue : Dans Scratch 1.4 elle apparaît dans le menu des langues, juste sous le français « officiel ». Son nom étant « français (Canada) ». Et là, heureuse surprise, on comprend beaucoup mieux ce que fait cette incrémentation sofusienne :

Alors là, on dirait vraiment du Cobol ! Dans un monde idéal, l’équipe de Scratch aurait tenu compte de la sagesse des québécois et aurait remplacé son bloc sofusien par « to n add 1 ». Et dans ce monde scratchien idéal, l’équipe responsable de la traduction « français officiel » aurait alors suivi, voire précédé (en français ça devait être facile) la traduction québécoise. Mais le monde de Scratch est loin d’être idéal, sinon la version 2.0 n’aurait jamais été programmée en Flash [3]...
En créole
La version créole (haïtien) de Scratch est encore plus mystérieuse :

« mettre n en place de 1 »...
Certes Haïti c’est le pays du vaudou, mais là, on fait mieux que l’affectation traditionnelle qui met 1 à la place de n, on remplace carrément des constantes par des variables !
Il est difficile de deviner de quelle langue s’est inspirée la version créole mais si c’est la version québécoise il y a là un phénomène linguistique particulièrement intéressant !
Scratch 2.0
De mieux en mieux, la version de Scratch qui sera utilisée dans tous les collèges de France et de Navarre dans quelques semaines, dit ceci :

Franchement, il n’est pas illusoire de penser qu’au cours de la simulation d’un programme de calcul, un collégien fasse quelque chose comme ceci :
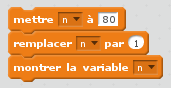
Il n’est pas illusoire non plus de penser que ledit collégien ait du mal à comprendre que n soit égal à 81 et non à 1 (« mais puisque j’ai remplacé n par 1, n devrait être devenu 1 et non 81, n’est-pas M’sieur ? »). Il n’est pas illusoire de penser que le prof de maths qui ne s’attendait pas à ce coup-là soit lui aussi surpris au point qu’il ait du mal à expliquer le comportement illogique du logiciel.
Comment après ces approximations syntaxiques, peut-on exiger de la rigueur d’adolescents qui n’en voient même pas dans le logiciel qu’on leur a imposé (ainsi qu’à leur prof) ?
Snap !
Snap ! est plus cohérent dans sa version française :

Sauf que des mots l’ordre pas très logique n’est [4] : « Ajouter 1 à n » est plus facile à comprendre que « Ajouter à n 1 », surtout s’il n’y a pas de virgule entre « n » et « 1 ».
Il est à remarquer que bien qu’il soit possible d’effectuer une opération in situ dans Snap ! comme le montre ce bloc, là non plus aucun effort n’a été fait jusque là pour généraliser ce genre de bloc, et Snap ! ne possède pas plus de « doubler » que son ancêtre Scratch [5].
Blockly
Blockly lui aussi s’inspire fortement de Scratch et lui aussi est développé en JavaScript. Voici comment sa tortue traduit le fameux bloc sofusien d’incrémentation en place :

Pas mal, à part le côté pléonasme (le plus souvent quand on incrémente c’est de 1). Il est dommage que le bloc « décrémenter de 1 » n’ait pas (encore ?) été ajouté à Blockly. Mais les techniques exposées ici permettent de fabriquer ses propres blocs et c’est la raison pour laquelle Sofus a été programmé dans Blockly et non dans Scratch : Dans le premier cas c’est possible, dans l’autre non...
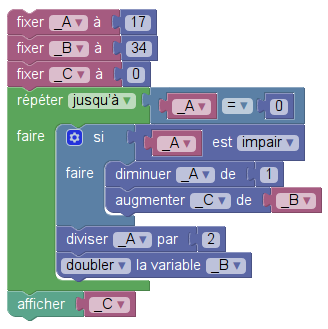
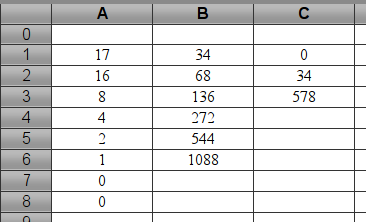
Comme souvent en algorithmique, l’usage du tableur contribue à repérer les valeurs successives des variables, tout simplement en les écrivant l’une en-dessous de l’autre dans une colonne (une colonne par variable) du tableur. Voici le rendu en 4 colonnes obtenu avec le tableur gnumeric :

Ce fichier a été obtenu de la manière suivante :
- Les nombres 17 et 34 à multiplier ont été placés en A1 et en C1 respectivement.
- Le reste de la division de 17 par 2 a été placé en B1, avec la formule =mod(A1 ;2)
- Le produit de C1 et B1 a été placé en D1 avec la formule =B1*C1 (comme ça si le nombre en A est pair, la multiplication donne 0 et on n’a pas besoin, à la fin, de test sur la parité ; c’est de l’algèbre de Boole) ;
- Dans la cellule A2 a été entrée la formule =(A1-B1)/2 qui effectue la division par 2 (après avoir soustrait le nombre 1 si A1 est impair, ce qui garantit que le résultat de la division est entier) ;
- Dans la cellule C2 a été entré le doublement avec =C1*2
- les contenus des cellules B1 et D1 ont été copiés vers le bas en B2 et D2 ;
- Puis toute la ligne 2 a été recopiée vers le bas, 10 fois.
- Enfin, dans la cellule D15 (choisie au hasard) a été entrée la formule =sum(D1:D12) qui donne le produit des nombres entrés en A1 et C1.
Voici le fichier obtenu (exporté en odt pour ne pas nécessiter d’installer un tableur libre, léger, gratuit et très adapté à la statistique inférentielle, merci qui ?), dans lequel il suffit de modifier les contenus de A1 et C1 pour calculer d’autres produits :
Outre le fait qu’avec ce fichier tableur, on a « privilégié le changement de cadre », la version tableur permet de poser une question qui n’avait pas de sens avec la version « algo » :
En allant jusqu’à la ligne 12 comme ci-dessus, quel est le plus grand nombre qu’on peut mettre dans A1 pour que le produit dans D15 soit correct ?
On remarque en passant que la question ne se pose pas pour le second facteur, et même, que cet algorithme ne montre pas que la multiplication est commutative.




Commentaires