Pour être en mesure de manipuler de manière collaborative une même figure géométrique, il faut un serveur et des clients. Le serveur et chacun des clients sont des instances du logiciel CaRMetal. Pour qu’on voie le mieux possible ce qui se passe lors de l’activité, il est idéal que le serveur soit vidéoprojeté. Ainsi chaque client verra simultanément l’effet des actions sur son écran, et l’effet global de l’ensemble des actions sur l’écran du serveur.
La première étape est donc que le prof et chacun des élèves démarrent CaRMetal sur un poste relié au réseau pédagogique du lycée. Le prof vidéoprojette son écran et insiste sur le fait que pour l’instant les élèves ne doivent pas faire la même chose que lui, à savoir démarrer un serveur. Pour cela, il va sur l’entrée réseau du menu de CaRMetal et choisit l’option démarrer un serveur :
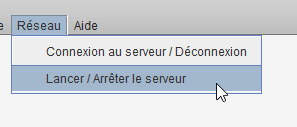
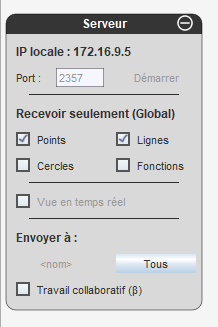
Cela a pour effet d’ouvrir ce cadre dans CaRMetal (toujours vidéoprojeté ; les élèves pour peu qu’ils soient attentifs, voient tout) :
On constate que le numéro de port (2357) est grisé parce qu’il n’est pas possible (pour l’instant) de le modifier ; il n’est donc pas nécessaire d’en parler. Le prof décoche les cases correspondant aux cercles et aux fontions parce qu’on n’en aura pas besoin dans cette activité [1].
Le prof recopie au tableau, en grand, l’adresse IP du serveur (ici c’est 172.16.9.5 mais ça dépend du réseau que l’on utilise évidemment), en disant aux élèves que cette information leur sera nécessaire pour se connecter. Puis il clique sur démarrer ce qui a pour effet ... de démarrer le serveur. Étonnant non ?
On constate que le bouton permettant de démarrer le serveur a disparu. Il faut dire que maintenant que le serveur est démarré, il ne sert plus à grand chose, ce bouton. Mais il reste la possibilité de cocher la case travail collaboratif :
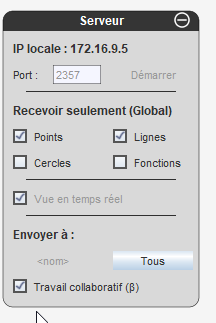
À partir de maintenant, tous les clients qui se seront connectés au serveur manipuleront la même figure qui s’appelle global (du moins du point de vue du serveur) :
Préparation des figures
Les élèves vont configurer CaRMetal pour que les points
- aient la forme d’un cercle (ils représentent les sommets d’un graphe)
- soient en gras (couleur remplie, pour faciliter les problèmes de coloriage)
- aient leur nom (ou plutôt leur alias) affiché dès la création
- soient en bleu (la couleur est modifiable après coup) au moment de la création)
- soient les plus grands possibles pour qu’on les voie de loin
Cela ressemble à ces réglages (à part l’oubli de cliquer sur « A » pour afficher le nom) :
Le serveur crée alors un point sur sa figure (« global ») puis les clients se connectent au serveur.
Le premier client se connecte en naviguant sur le menu réseau mais attention, il ne doit pas cliquer sur lancer un serveur mais sur connexion au serveur. Il lui est alors demandé un identifiant (ici, client1) et l’adresse IP du serveur auquel il souhaite se connecter. C’est ici qu’il est utile d’avoir écrit cette adresse (172.16.9.5 dans l’exemple ci-dessous) au tableau, puisqu’il faut la taper au clavier :
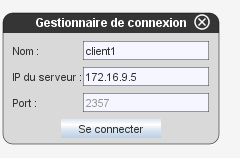
Une fois que le client a cliqué sur se connecter le serveur connaît son nom et son adresse IP (172.16.15.155 ci-dessous) :
Création d’un point
Le client 1 va se dessiner sur le graphe, en créant un point qu’il va nommer client1 (sous forme de l’alias du point) puis tracer un segment (en vert) allant du point serveur (déjà visible sur la figure commune au client et au serveur) et enfin bouger ce point avec la souris. On voit successivement ces figures :
Création et renommage du point représentant le client :
Création de l’arête joignant les deux sommets du graphe :
Mouvement du sommet représentant le client :
| côté client | côté serveur |
|
|
Voir la figure évoluer en même temps sur son propre écran et celui du prof, est une expérience magique, aussi d’autres clients ne tardent-ils pas à se connecter eux aussi.
Le second client vit une expérience très similaire à celle du client 1 : Seul son nom est différent, il entre la même adresse IP (celle du serveur, soit 172.16.9.5) pour se connecter à son tour :
Une fois la connexion effective, le serveur sait que l’adresse IP du client 2 est 172.16.15.154 :
Création du second point
Lorsque le client 2 crée son point, le serveur voit quelque chose de ce genre :
puis, après renommage du point et création de l’arête par le client :
Alors que le client 2 voit, en même temps, ce qu’il a créé :
Exemples
On propose ici des exemples d’activités mettant en œuvre la possibilité de dessiner et modifier des graphes en travail collaboratif, avec CaRMetal :
- Représenter par un graphe le réseau serveur/clients (intranet) que l’on vient de mettre en place
- Imaginer, dessin de graphe à l’appui, d’autres topologies du réseau intranet, ainsi que la liaison entre plusieurs réseaux intranet (« internet »)
- Représenter un réseau social par un graphe et calculer les distances remarquables apparaissant dans ce graphe
- Colorier collaborativement un graphe
Intranet
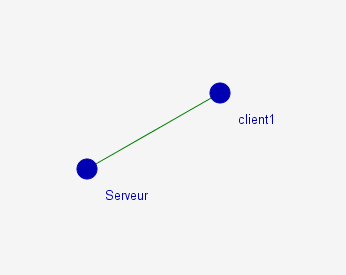
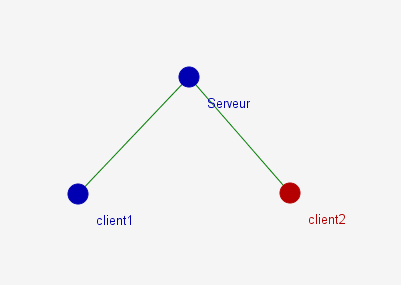
Comme tous les clients sont connectés au serveur, il est impossible à deux clients de communiquer directement entre eux, ils doivent pour cela passer par le serveur :
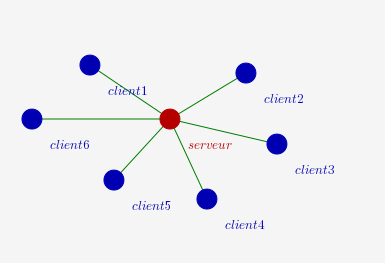
Le serveur est le centre du graphe : Il est le plus proche possible de tout le monde à la fois, puisque sa distance à chaque client est 1. Cette distance minimale est le rayon du graphe.
Par contre, chaque client est plus proche de lui-même que le serveur, mais plus éloigné des autres clients : Pour communiquer avec un autre client il doit passer par le serveur, donc il est à distance 2 de chaque autre client : Cette distance est le diamètre du graphe.
Peer-to-peer
La topologie précédente, qui est un graphe étoile, est fragile, car en cas de panne du serveur, tout le réseau est en panne. On peut lui préférer l’architecture où tout client est serveur en même temps : L’architecture « pair à pair » (pear-to-pear en anglais) correspond, idéalement, à un graphe complet.
Le graphe complet à 15 sommets comprend 105 arêtes ce qui est long à dessiner si on est seul. Le travail collaboratif de CaRMetal peut aider ici, en demandant à chaque client de tracer les 15 arêtes le concernant (en réalité moins puisque certaines arêtes sont dessinées par d’autres clients).
Le graphe complet a ceci de remarquable
- que tous ses sommets sont des centres
- que son rayon vaut 1
- que son diamètre aussi vaut 1.
Internet
Si on relie plusieurs intranet (ici en étoile) par des routeurs eux aussi disposés en étoile, on obtient une structure arborescente. Voici un arbre pouvant représenter Internet ’ordinateurs en bleu, serveurs intranet en rouge, routeurs internet en vert) :
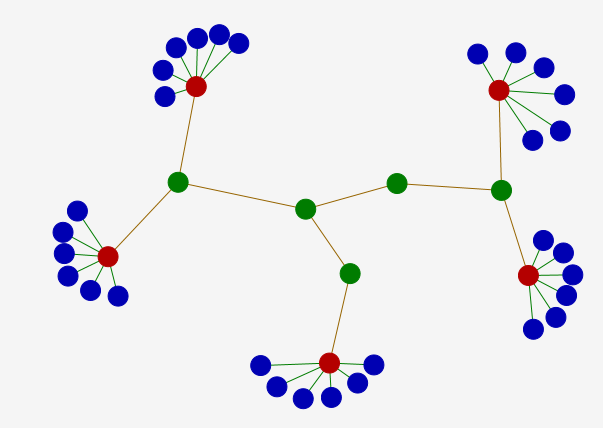
Cet arbre est de diamètre 7 et de rayon 4. Et il est soumis à la même fragilité que les intranets en étoile. On lui préfèrera donc un système où l’intranet est en étoile et l’internet un graphe complet, comme ceci :
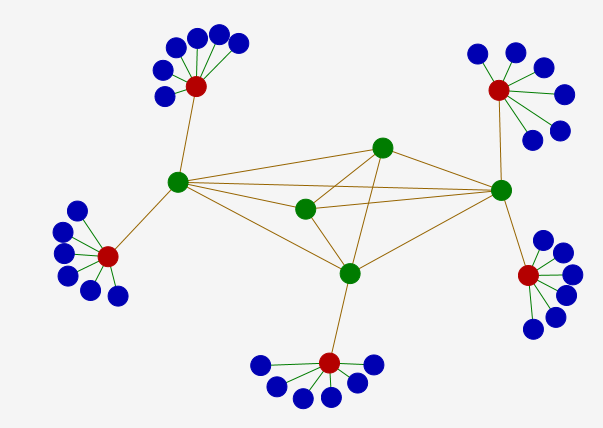
Celui-ci est de rayon 2 et de diamètre 5.
On remarque que les notions de rayon et diamètre d’un graphe, présentées dans le thème 3 du programme de SNT, sont intéressantes à étudier aussi dans le thème 1.
réseaux sociaux
Voici un exercice typique du thème 3 de SNT :
Comme le rayon et le diamètre d’un graphe connexe sont les valeurs extrémales de l’excentricité des sommets du graphe, on peut, même si cette notion n’est pas explicitement au programme, faire calculer et écrire (comme alias des sommets) les excentricités des sommets, en travail collaboratif : Il suffit que chaque élève soit associé à un sommet et se charge de calculer les distances séparant ce sommet de tous les autres sommets : L’excentricité est le maximum de ces distances.
Coloriage
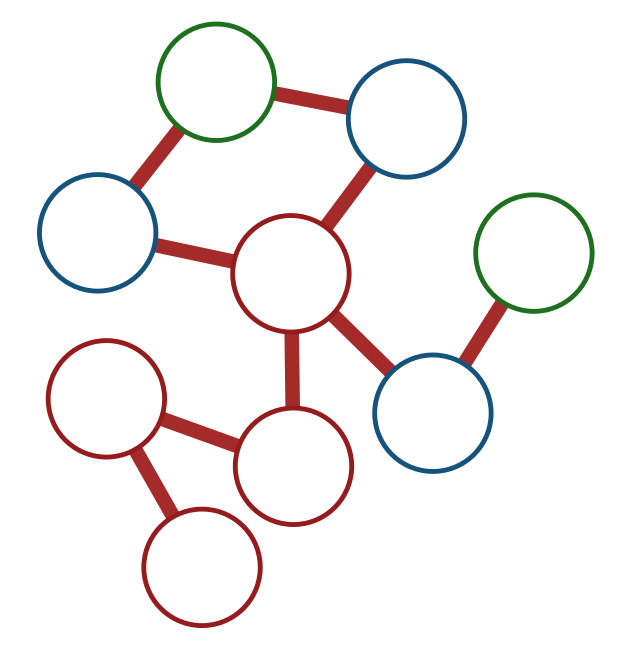
Voici un graphe difficile à colorier en 4 couleurs : Son coloriage est peut-être plus aisé en calcul parallèle, comme cela avait été tenté à Grand-Coude l’année dernière, sous le nom de « jardin de McGregor » :
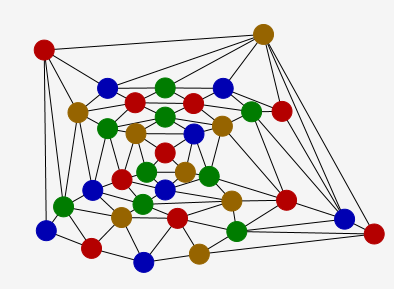
Commentaires