Objectifs / Prérequis

L’objectif de cette séance était que les élèves découvrent par eux mêmes comment calculer l’aire d’un triangle. La notion d’aire a déjà été rencontrée plusieurs fois, et les élèves savent calculer l’aire d’un rectangle ainsi que l’aire d’un triangle rectangle. Ils ont également travaillé, en 6^e et dans les classes antérieures, la notion d’aire par pavage.

Déroulement de la séance

Dès l’arrivée en classe, je les informe que l’on va travailler en groupe pour la résolution d’un problème. Ils savent donc rapidement se retrouver en groupes (les mêmes qu’aux autres séances), installer les tables...
J’énonce donc assez rapidement le problème.
Je les préviens que ce travail est noté, et que je ramasserais en fin d’heure la feuille réponse d’un élève dans chaque groupe, et que donc chaque élève doit avoir sa propre copie !
Je les laisse quelques instants préparer leur feuille, écrire le titre et comprendre la question, puis je leur explique le terme « quelconque » qui n’avait pas été rencontré jusqu’à maintenant et qui aurait pu être un obstacle pour certains.

Tous les groupes se lancent dans l’activité, en commençant par tracer un triangle sur leur feuille (le même pour tous les élèves d’un même groupe) avec des dimensions quelconques.
Je n’ai vu aucun triangle rectangle ni isocèle.
Puis, s’appliquant à bien poser la multiplication, la majorité des groupes multiplient les longueurs de deux côtés, pour ensuite diviser le résultat par deux.

Je passe de groupe en groupe, en leur demandant pourquoi ils pensent que leurs calculs donnent l’aire du rectangle, et pourquoi avoir choisi ces deux côtés plutôt que deux autres... Dans un groupe c’est parce que c’étaient les plus grands côtés... Dans un autre parce que c’étaient les plus petits !!!
Je tente alors de les faire réagir en leur traçant un triangle ayant ces deux longueurs en commun, mais en changeant le troisième côté, de façon à ce que l’aire du triangle soit très visiblement très différente.
Pour certains, l’argument sera suffisant, et ils chercheront une autre piste. Pour d’autres je n’ai apparemment pas été très convaincante, car malgré les autres pistes de recherche que j’ai lancées plus tard, ils ont gardé leur idée et m’ont rendu leur copie finale avec cette même démarche...

D’autres groupes ont eu de bonnes idées et une démarche beaucoup plus scientifique, partant de ce qu’ils savaient faire : calculer l’aire d’un triangle rectangle.
Ils ont alors sans le savoir tracé une hauteur du triangle...

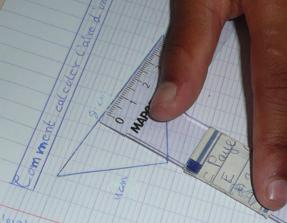
… Mais hélas n’ont pas abouti... De ce que j’ai pu voir, c’est le fait de travailler en groupe qui les a bloqués, chacun d’entre eux ayant une idée différente et n’arrivant pas à l’expliquer à ses camarades... Une élève m’a même dit : « on n’arrive pas à se comprendre, on part dans tous les sens... »

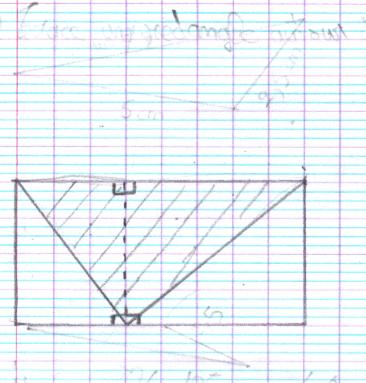
Au bout de 25 minutes de recherche, j’ai donné une piste à toute la classe, pour aider ceux qui étaient en train de se décourager... Je leur ai dit de partir d’un rectangle et d’y inscrire un triangle, en leur faisant plusieurs schémas au tableau...

Plusieurs groupes ont senti qu’il fallait calculer l’aire des deux triangles rectangles, mais aucun n’a réussi à avoir une démarche aboutie.
Cet exemple montre leur confusion : au lieu de calculer séparément les aires des deux triangles, ils ont additionné les longueurs de deux côtés et multiplié par la hauteur...

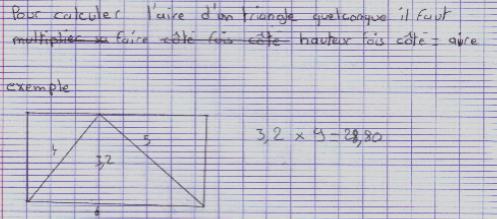
Et d’autres qui étaient sur la piste ont compulsivement effacé tous leurs calculs avant de me rendre leur copie...

Evaluation

Pour cette activité, j’ai évalué et noté le travail de quelques élèves, comme convenu en début d’heure...
J’ai rempli un tableau contenant les items suivants que j’ai collé sur leur copie :

Critères d’évaluation
Pilier 3 :
Rechercher, extraire et organiser l’information utile
Calculer. Appliquer des consignes
Engager une démarche, raisonner, argumenter, démontrer
Présenter la démarche suivie, les résultats obtenus à l’aide de langages scientifiques

Pilier 6 :
Connaître, comprendre et respecter les règles de la vie collective

Pilier 7
Savoir travailler en groupe. Prendre des initiatives

La notation, peu sévère à mon avis, était répartie de la manière suivante : 1 point si la méthode était trouvée, 1 point par capacité du socle réussie. Le travail était donc noté sur 7. Tous ont eu la moyenne, même si personne n’a trouvé la bonne formule.

Ce que j’attendais d’eux pour qu’ils aient « Réussi »...
– Rechercher, extraire et organiser l’information utile : Comprendre le problème, chercher une méthode, calculer une aire, réfléchir pour un triangle quelconque...
– Calculer. Appliquer des consignes : Là j’ai surtout regardé le « appliquer des consignes » en notant s’ils avaient cherché une méthode pour calculer l’aire...
– Engager une démarche, raisonner, argumenter, démontrer : Faire une figure, faire des essais, réagir face aux résultats obtenus...
– Présenter la démarche suivie, les résultats obtenus à l’aide de langages scientifiques : répondre à la question en donnant une explication, utiliser correctement le vocabulaire « aire » et « cm2 »...
– Pour les autres items, cela revenait à évaluer leur attitude face à un travail en groupe.

Bilan

Le bilan de cette séance est très positif, car même si aucun groupe n’a trouvé la bonne méthode, encore une fois tous les élèves ont vraiment travaillé et ont essayé !
J’ai pu me rendre compte qu’ils ne confondaient plus aire et périmètre, qu’ils savaient poser et effectuer une multiplication décimale, que beaucoup ont commencé à chercher dans la bonne direction et donc avaient correctement analysé le problème...
Au niveau du travail en groupe, c’était plutôt bien, ils essayaient vraiment de travailler ensemble.
Je vois aussi clairement leurs difficultés : pour eux une formule mathématique c’est une formule magique, qui sort un peu de nulle part, pourvu qu’il y ait des calculs à faire ! Ils sont encore très loin d’avoir du recul pour comprendre les contre exemple. Enfin beaucoup avaient dessiné le schéma idéal mais n’ont pas su s’en servir...

J’ai volontairement limité la séance à 55 minutes. Certes si j’avais laissé plus de temps certains auraient peut-être abouti, mais pour d’autres ç’aurait sûrement été l’enlisement total, et il m’aurait été difficile de « tenir » la classe...
La séance suivante fut celle du bilan en classe entière, où chacun pouvait participer puisque tous avaient, à leur niveau, réfléchi à la question...