J’ai découvert Snap! début 2016, grâce à un petit mail de Yves Martin, je le remercie infiniment. [1]
[2]
Bref prélude : LOGO et Scratch
Entrée en matière

J’avais commencé la programmation visuelle avec LOGO, conçu par Seymour Papert, dès mes débuts d’enseignante, en 1991 [3]. J’ai une grande admiration pour Seymour Papert et sa conception de l’enseignement des mathématiques. Nous devrions tous lire ou relire Jaillissement de l’esprit. Ordinateurs et apprentissage [4], aux Éditions Flammarion, 1981, car dans ce livre, Seymour Papert pointait déjà du doigt l’enseignement des mathématiques. Sans complaisance, il expliquait pourquoi cet enseignement, tel qu’enseigné alors, conduisait souvent à la phobie des mathématiques. Chercheur et concepteur de logiciels au laboratoire d’intelligence artificielle du MIT, il a consacré sa vie à réfléchir et à faire des expérimentations sur l’enseignement des mathématiques (et aussi de la physique newtonienne) [5].
En relisant ce livre, on s’aperçoit que nous en sommes toujours au même point en France quant à l’enseignement des mathématiques, avec une incompréhension des mathématiques de la part de nos élèves, incompréhension grandissant avec l’évolution du numérique dans la société. Mais, enfin, l’illustration d’algorithmes par leur codage demandée dès le collège (voire dès l’école primaire), est en train d’ébranler une conception archaïque et inadaptée aujourd’hui de l’enseignement des mathématiques.
Le codage arrive partout. Et c’est un phénomène mondial. En 2013, Obama engage les jeunes américains à apprendre à programmer : « President Obama asks America to learn computer science ».
En France, dans l’Éducation nationale, il y a déjà quelques années que les algorithmes sont entrés dans les programmes de mathématiques au lycée (une vingtaine d’années déjà…). Le site académique de mathématiques de la Réunion icosaweb.ac-reunion.fr avait d’ailleurs de très riches ressources en algorithmique. [6]
Mais la programmation en tant que telle n’est entrée dans les programmes de lycée que très récemment (rentrée 2012) avec la spécialité ISN en terminale S.
Quelques enseignants seulement allaient jusqu’à la phase de codage lorsqu’ils élaboraient des algorithmes avec les élèves en classe de mathématiques, soit avec un logiciel, soit avec une calculatrice.

Depuis cette rentrée (2017-2018), le codage et la programmation sont officiellement dans les programmes de collège et d’école primaire. Je dis bien programmation, pas seulement algorithmique. Et l’utilisation du logiciel libre Scratch pour programmer en classe a largement été préconisée par le ministère de l’Éducation nationale. [7]
J’ai montré dans cet article que « Scratch est idéal pour mettre en œuvre de manière ludique et rapide des algorithmes en classe de seconde » et je fais programmer avec Scratch, entre autres [8], dans mes classes de lycée depuis la rentrée 2009. Vous trouverez dans cet autre article, de nombreux exemples de scripts écrits pour débuter en algorithmique de manière progressive avec Scratch.
Snap! : le Scratch qui code du code
Snap! — Build your own blocks — est un langage de programmation visuel en mode glisser-déposer développé par l’université de Berkeley. Snap! est une implémentation largement étendue du code source du logiciel Scratch du MIT Lab. Logiciel libre développé en HTML5 sous licence GPL3, il est développé par Jens Mönig et Brian Harvey. [9].
Snap! est donc une page html et se lance en ligne dans un navigateur mais peut aussi se déployer en local (à partir des sources que l’on télécharge sur Github).
Snap! permet — et c’est de là qu’il tire toute sa puissance — de programmer et d’écrire ses propres blocs (équivalent de la notion de fonction dans le logiciel), d’où son nom d’origine : Build your own blocks.

Snap! permet de faire de la programmation fonctionnelle, et c’est ce qui fait sa force.
En quelques mots, qu’est-ce que la programmation fonctionnelle ?
La programmation fonctionnelle considère le calcul en tant qu’évaluation de fonctions mathématiques. Un programme est donc une application, au sens mathématique du terme, qui ne donne qu’un seul résultat pour chaque ensemble de valeurs en entrée.
Un langage de programmation fonctionnelle doit permettre de passer des fonctions en paramètre, car les langages fonctionnels emploient des types et des structures de données de haut niveau comme les listes extensibles. C’est ce que Jens Mönig appelle des variables first-class [10].
J’ai présenté Snap! à l’IREM de la Réunion le 14 juin 2016 à l’aide d’une carte mentale que je joins en bas de cet article.
J’y démontrais entre autres que Snap! est un langage de programmation qui répond à tous les critères de choix d’un langage idéal pour l’enseignement du codage à l’école [11]. Je joins également un plan de cet exposé en mode texte [12]. Ce plan précise les idées essentielles qui y ont été abordées.
J’y développais aussi pourquoi j’ai été littéralement subjuguée, à la fois par la facilité de programmation que Snap! procure et par les champs d’applications possibles qu’il laisse entrevoir.
Snap! permet de créer des blocs simples très rapidement et d’implémenter des fonctions et processus récursifs simples.
Depuis cette rentrée scolaire, j’utilise Snap! en classe pour accompagner le cours dans mes classes (seconde, première S, seconde ICN et parfois en première STMG) et surtout pour programmer et illustrer des algorithmes écrits avec les élèves. Parmi les élèves, Snap! fait l’unanimité, lors de son utilisation, dès la première séance. La prise en main est assez immédiate et la pratique régulière familiarise les élèves rapidement avec son environnement.
Plus je l’utilise en classe, plus je le trouve adapté à l’enseignement des mathématiques.
Scratch ou Snap! en classe ?
Peu importe au final, le principal, c’est de faire agencer des blocs de scripts aux élèves dans le bon ordre afin qu’ils apprennent à créer, comprendre et à lire un code source déjà écrit. Cela correspond à mon sens à l’apprentissage de la lecture d’une langue étrangère ayant un alphabet différent du nôtre (exemple : le chinois). La phase d’écriture peut venir bien plus tard, et sera d’autant plus facile à aborder que la lecture aura été comprise.
Il me semble que cela est beaucoup plus facile d’apprendre à lire que d’apprendre à écrire, car savoir lire relève juste d’une mémoire visuelle, tout comme savoir reconnaître des blocs de programmation. Il ne s’agit pas de faire de nos élèves des programmeurs, mais il s’agit bien de leur faire comprendre ce qu’est un algorithme, et de leur en faire créer et exécuter. Il ne s’agit pas de les écrire car cela ajouterait la difficulté liée à la syntaxe du langage de programmation choisi.
Autant se consacrer à l’essentiel : la compréhension des algorithmes.
– Scratch va sortir une version 3 basée sur Blockly. On peut déjà avoir une idée du rendu ici.
Cette version 3 de Scratch sera présentée au colloque international Scratch 2017 qui se déroulera à Bordeaux du 19 au 21 juillet 2017. Scratch2017BDX sera dédié au 10e anniversaire de Scratch et au 50e anniversaire de son prédécesseur, LOGO. J’y présenterai cette communication sur la programmation visuelle : « From Scratch to Snap!, what visual programming brings to my students. »
Lors d’une interrogation publique postée sur la liste educ@april.org de l’April le 2 mars 2016 sur le choix de Scratch ou de Snap! pour programmer en classe, je mettais en avant les atouts de Snap! :
– Snap! est codé en HTML5, son exécutable est donc une page HTML/javascript de quelques Koctets.
– Le logiciel est libre sous licence Gnu Affero GPL version 3, ses sources sont donc téléchargeables sur son dépôt dédié sur Github et donc Snap! est utilisable en local en classe.
– Les projets Snap! se sauvegardent soit au format XML (toujours seulement quelques kilooctets), par le menu « Exporter », soit sur le cloud de l’université de Berkeley dédié à Snap!, soit dans un dossier local lié à votre navigateur.
– Codage de blocs avec paramètres d’entrée avec ou sans retour (véritable fonction au sens mathématique du terme : nous sommes au coeur de la notion universelle de fonction soulignée dans le nouveau programme de seconde soumis à la lecture des enseignants).

|
– Il est aussi très simple dans Snap! de créer des procédures récursives telle que n !.
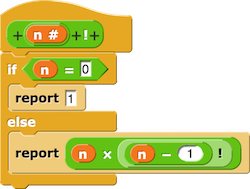
|

|
– Ce logiciel open-source permet de créer un exécutable « stand-alone » de son projet, et cela est proposé pour les trois plateformes : Linux, Mac et Windows ! [13]
– Ce logiciel en ligne est dédié à la transcription de projets Scratch en Snap!, ce qui permet d’importer des projets Scratch dans Snap! [14].
– Il existe un forum consacré au logiciel. Les développeurs répondent volontiers et sont en général très réactifs.
La réaction d’un enseignant [15] à cette interrogation publique est donnée au bas de cet article [16].
Arrêtons nous un moment sur le lutin de Snap! par défaut.
– Le lutin de Snap! par défaut est issu de ce que Seymour Papert appelle la géométrie tortue.
Cette géométrie tortue créée par Seymour Papert est une géométrie dynamique informatique.
La géométrie d’Euclide repose sur une entité fondamentale qui est le point et un certain nombre d’axiomes. Le point d’Euclide n’a aucune propriété intrinsèque : ni dimension, ni couleur...
La géométrie tortue, elle, repose sur « La tortue » — entité fondamentale de la scène (notre univers sur l’écran) (car ici, il s’agit bien d’une géométrie exclusivement réalisable sur un ordinateur avec sortie écran) — qui est dynamique.
En effet, la tortue est définie par sa position et son orientation.
Le lutin de Snap! par défaut a une forme qui respecte scrupuleusement les consignes de Seymour Papert dans son livre Jaillissement de l’Esprit. La tortue (ici le lutin ou sprite en anglais) possède bien une position et une orientation. |
Dans la géométrie d’Euclide, les segments et les angles ne sont pas orientés : en fait, lorsqu’on dessine sur le papier, l’oeil et le cerveau décident inconsciemment du sens dans lequel il faut avancer ou tourner. Dans Snap!, qui relève d’une géométrie tortue, les segments et les angles sont orientés (c’est incontournable : l’ordinateur ne peut pas décider du sens tout seul), ce qui conduit inévitablement à utiliser des nombres négatifs. Ainsi, en programmation visuelle, les élèves utilisent spontanément des nombres négatifs (avance de -10, tourne de -30) avant même d’étudier le chapitre sur les nombres relatifs. Snap! familiarise d’entrée les élèves avec la géométrie moderne (orientée) et conduit les élèves à introduire d’eux-mêmes les concepts de nombre négatif et de repérage pour répondre à un besoin. | 
|
J’ajouterai en vrac aux multiples atouts de Snap! :
– Nombreuses bibliothèques externes à charger qui facilitent le développement. (Pourquoi réécrire ce qui a déjà été fait ?)
– Navigation aisée dans les scripts car l’interface est pensée avec ergonomie.
– Qualité du rendu des images de scripts.
– Une documentation riche est d’ores et déjà disponible en anglais ici.
– Importation des costumes et des sons par simple glissé-déposer dans la zone réservée à cet effet.
– Activation possible d’un mode pas à pas pour le débogage et pour aider le programmeur à comprendre ce qui ne fonctionne pas. C’est très utile pour que l’élève comprenne une erreur de raisonnement.
– Possibilité de mettre en pause l’exécution d’un programme. C’est utile pour noter des valeurs par exemple lorsque l’on n’a pas encore codé leur stockage, ou réalisé une copie d’écran de la scène à un état donné.
– Activation possible d’un mode Turbo.
Et la liste est loin d’être exhaustive...

|
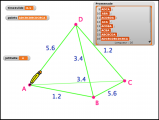
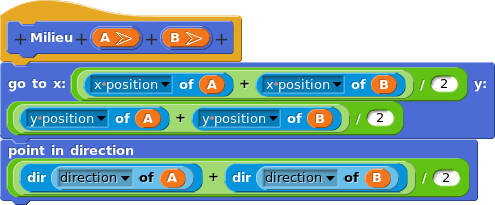
Sur cette image, 5 lutins
– A, B, C, – le milieu de [AB], – le centre de gravité du triangle ABC. En dynamique, on peut demander aux élèves Qui est qui ? |
| Quand on programme dans Snap!, on est tout le temps en train de réfléchir aux objets qu’on manipule. Qu’est-ce qu’un point ? Qu’est-ce que cette variable ? un réel ? une liste ? une fonction ? un lutin ? Qu’est-ce qu’un lutin exactement ? Par quoi est-il défini ? Quels sont ses attributs ou propriétés ? C’est parfois difficile, mais à mon sens, excellent pour faire réfléchir les élèves sur les objets mathématiques. Et puis, par les lutins (ou particules), nous sommes au coeur même de la physique newtonienne. |
De plus, les développeurs sont très actifs. Dans la liste des « ToDo » j’ai relevé une future exportation des images au format svg... Alors là, ce sera « la grande classe » côté graphisme.
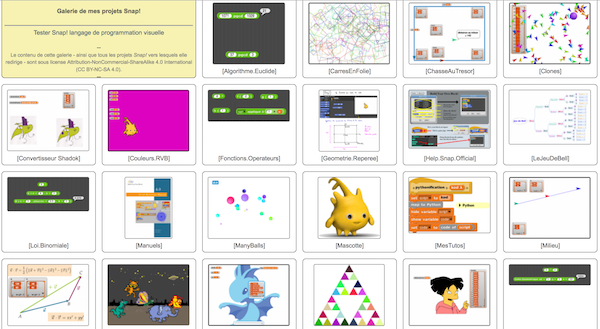
La visite de la galerie d’images d’un choix de scripts créés avec Snap! depuis plus d’un an vous éclairera sur la puissance de Snap!. Chaque script est accompagné d’un lien qui mène au projet en ligne sur le cloud de Berkeley. Chaque script est aussi téléchargeable au format xml (faire importer ensuite dans Snap! pour l’ouvrir).
La galerie étant sous licence Creative Commons Non Commercial Share Alike, vous pouvez copier, modifier et redistribuer à souhait ces projets, sous réserve d’en citer la provenance.
Beauté du code source en images

La beauté du script qui en résulte parfois m’a donné l’idée de créer cette galerie d’images de scripts. Je veux convaincre par l’image de la force de Snap!.
J’ai d’ailleurs présenté cette galerie d’images en mode Sans paroles lors du séminaire IREM du 14 avril 2017 pendant 25 min, présentation suivie d’un débat de 20 min.
Parfois, les mots sont inutiles.
Lisons ensemble ce poème extrait de Jaillissement de l’Esprit, en préliminaire du chapitre IV.
À lire page 42 dans le lien « Mindstorms » au bas de cet article.
Le mille-pattes allait insouciant
Quand le crapaud, en plaisantant,
Lui dit : "Très cher, quand vous marchez,
Ce doit être bien compliqué
De savoir quelle patte avancer ? "
Le mille-pattes en fut si troublé
Qu’il se retrouva au fossé,
Son millier de pattes emmêlé...(Anonyme)
J’adore l’image qui en ressort...
Cette citation soulève le problème d’une pensée trop conscientisée qui peut mener à l’écroulement d’une action entreprise. C’est pour cela, que parfois, en classe de mathématiques, il est bon à mon sens de laisser les élèves créer et découvrir avec Snap! en leur ayant donné quelques consignes pour démarrer. Les notions mathématiques suivront nécessairement. Je pense que l’une des raisons de l’échec de l’enseignement des mathématiques jusqu’à récemment, vient de la notion de rigueur même liée aux mathématiques que l’on a voulu inscrire dans les programmes. Faisons d’abord des mathématiques concrètes, et après, formalisons les, avec rigueur bien sûr. Mais chaque chose en son temps...
Je vous propose maintenant un guide de navigation à travers la galerie snap.nathalierun.net.
– > Premier script avec Snap!

|
– > Repérage dans le plan
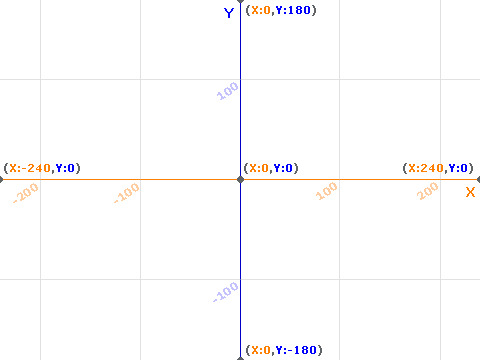
Dès que l’on veut utiliser la scène sur laquelle les objets vont être représentés, on a besoin de connaître le système de coordonnées.
La scène est un rectangle qui mesure par défaut : 480 pixels de large par 360 pixels de haut. Mais Snap! permet de modifier les dimensions de la scène. Après, il faut réfléchir au préalable sur ce que nous voulons comme rendu final. On peut garder les mêmes proportions et passer en 800x600 [17] si l’on veut une plus grande scène et une meilleure définition du rendu sur l’écran.
Du coup, les élèves doivent obligatoirement apprendre à se repérer, et à déplacer leur(s) lutin(s) sur cette scène.
On pourra aller voir les projets de géométrie analytique, qui permettent de couvrir le programme de seconde pour tout ce qui concerne le repérage (repère, coordonnées, milieu, distance, vecteur, équation de droite affine).
L’animation Chasse au Trésor sort tout droit de l’activité 2 page 116 du Sésamanuel de seconde. Cette activité est d’une richesse incroyable et aborde un grand nombre de notions du programme de seconde. Utiliser l’animation permet aux élèves de découvrir par eux-mêmes le sens de variation de la fonction distance du joueur au trésor.
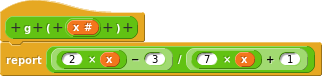
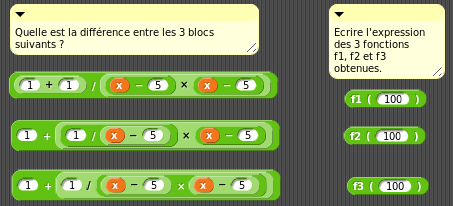
– > Fonctions et opérateurs
Les fonctions peuvent être vues absolument partout, dans tous les projets, car la notion de fonction en mathématiques de lycée est universelle.
Je me limite dans ce paragraphe à quelques exemples de fonctions à variables réelles.

| |

| |

| |
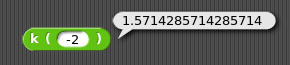
|
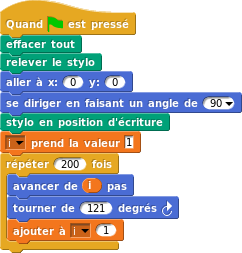
– > Promenades aléatoires
Ces promenades m’ont été inspirées par la lecture d’une fiche de statistiques du document d’accompagnement de seconde des programmes de juin 2000 (« Onze fiches de statistique »). En 2010, je faisais simuler ces promenades aléatoires sur tableur par les élèves (voir cet article sur les simulations). Puis l’idée m’est venue de le faire avec Scratch.
Vous trouverez dans la galerie quelques promenades réalisées importées dans Snap!.
[18]
– > Algorithme d’Euclide
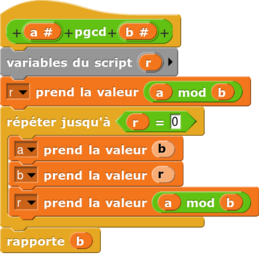
|

|
– > Clonage avec Snap!

– > Suites en première
Pour introduire les suites, j’ai demandé à mes élèves de dessiner le triangle de Sierpinski, avec les consignes suivantes :
FRACTALE DE SIERPINSKI
**********************
Données : Triangle ABC, n le n°d'étape
(le triangle ABC seul représente l'étape 0)
Initialisations :
Triangle ABC
A* milieu de [BC]
B* milieu de [CA]
C* milieu de [AB]
Remplir les triangles BA*C*, A*CB*, C*B*A
Laisser vide le triangle A*B*C*
Recommencer le processus précédent sur chacun des 3 triangles
BA*C*, A*CB*, C*B*A jusqu'à l'étape n.
Construire les étapes 1, 2, 3, 4 et 5.
A chaque étape : donner :
- le nombre de triangles colorés Tn
- leur côté cn
- leur aire individuelle an
- leur périmètre individuel pn
- l'aire totale du domaine couvert An
- le périmètre total des triangles Pn
Ce qui a été fait en classe est ici.
Ci-dessous les calculs faits avec Snap!, à retrouver dans la galerie dans le dossier Sierpinski.


Ce qui me plaît aussi avec Snap! , c’est que l’on peut réaliser de belles choses. |


– > Simulations, Couleurs RVB et autres friandises...
Notons juste ici que le clonage rend les simulations de jeux tels que le jeu de la vie de Conway et autres automates cellulaires très accessibles, pour réaliser du codage consistant en Terminale S ISN.
La galerie propose une simulation réalisable en seconde autour des familles de quatre enfants. Il est amené à être complété et amélioré.
Elle propose également un codage des couleurs RVB afin d’en comprendre le fonctionnement. Cela a déjà fait l’objet de cet article détaillé, Rouge, Vert, Bleu, de 0 à 255.
Vous trouverez également un calcul de loi binomiale, de produit scalaire, un projet sur le second degré, un calcul de la mesure principale d’angles orientés, un convertisseur Shadok, et ce n’est que le début...
Carte mentale de navigation dans la galerie
Je vous souhaite une bonne découverte (ou utilisation) de Snap! ainsi qu’une bonne visite de cette galerie d’images.
Remarque : J’aurais pu mettre dans cet article des liens directs vers chaque notion de la galerie que je souhaite mettre en avant, mais comme cette galerie est amenée à être alimentée régulièrement, les liens ne seraient plus valides [19]. Je vous laisse donc la découvrir seuls, ou linéairement en suivant les points abordés précédemment, ou plutôt à travers cette carte mentale de navigation :







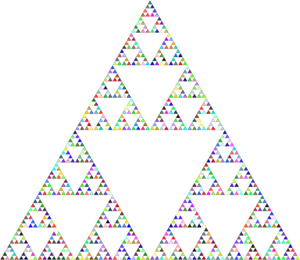

Commentaires