matériel
L’abaque de Gerbert (à imprimer au format A3 sauf si les jetons sont petits) :
Le nomogramme (au format A4) :
Pour les jetons de Gerbert, des tranches de cylindres (tringles à rideau en bois, bouchons de vin, etc) avec des chiffres écrits dessus, font l’affaire. Une machine à découpe laser permet de fabriquer des jetons en contreplaqué, et on peut même envisager d’imprimer en 3D des jetons avec chiffres en relief.
Séance en début de CE 2
Pour éviter d’aborder l’activité trop tard dans l’année (par exemple, lorsque les élèves sont déjà trop formatés « calcul écrit »), une séance a été menée presque au tout début de l’année scolaire, en CE2 b de l’école Aristide-Briand (Le Tampon). En voici le compte-rendu, en trois étapes :
- Activité préliminaire avec les réglettes Cuisenaire :
- Appropriation du nomogramme par les élèves (la phase ayant eu le plus de succès) :
- Abaque de Gerbert pour la multiplication :
L’observation des problèmes rencontrés durant cette séance mène à la proposition suivante, de progression durant les deux années de CE 2 et CM1, sur l’apprentissage de la multiplication :
Voici un exemple de séance a priori abordable durant l’année de CE 2 (période 2 ?) :
Un jardinier doit planter 12 rangées de 13 fleurs chacune. Combien de graines doit-il semer pour cela ?
Il s’agit donc de multiplier 12 (rangées) par 13 (fleurs par rangée). Le jardinier décide alors d’organiser les 12 rangées en
- 10 rangées constituées de
- 10 fleurs blanches
- 3 fleurs rouges (cela fait bien 13 fleurs par rangée)
- 2 rangées constituées de
- 10 fleurs rouges
- 3 fleurs blanches (cela fait aussi 13 fleurs par rangée)
Il envisage donc ce motif :
Cela lui permet de mieux dénombrer le nombre total de fleurs, regroupées en
- 10 rangées de 10 fleurs blanches, soit 10×10 fleurs blanches,
- 2 rangées de 3 fleurs blanches, soit 2×3 fleurs blanches en plus,
- 2 rangées de 10 fleurs rouges, soit 2×10 fleurs rouges,
- et 10 rangées de 3 fleurs rouges en plus (soit 10×3 fleurs rouges en plus) :
Pour les 10 rangées de 3, c’est plus compliqué, mais en tournant la figure
on constate que cela revient à 3 rangées de 10 fleurs rouges chacune : 10×3 = 3×10.
Donc le nombre total de fleurs est la somme de ces 4 nombres. Linguistiquement, on utilise l’associativité de la multiplication, selon laquelle
- deux fois trente,
- c’est deux fois trois dizaines, plus précisément deux fois (trois dizaines), donc c’est
- (deux fois trois) dizaines selon l’associativité, donc c’est
- six dizaines, soit
- soixante.
Avec cela, les quatre termes de 12×13 deviennent :
- 10×10, c’est dix dizaines soit une centaine :
| centaines | dizaines | unités |
| ① |
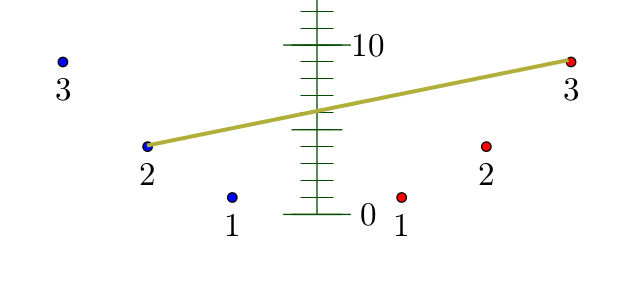
- 2×3, c’est six, comme on peut le vérifier sur le nomogramme si l’apprentissage des tables de multiplication est en cours d’acqusition :
| centaines | dizaines | unités |
| ① | ||
| ⑥ |
- 2×10, c’est deux dizaines :
| centaines | dizaines | unités |
| ① | ||
| ⑥ | ||
| ② |
- 10×3, c’est la même chose que 3×10, soit trois dizaines :
| centaines | dizaines | unités |
| ① | ||
| ⑥ | ||
| ② | ||
| ③ |
Ensuite on peut remplacer les jetons ② et ③ de la colonne des dizaines, par un seul jeton ⑤ dans la même colonne, puisque deux dizaines plus trois dizaines, cela fait cinq dizaines :
| centaines | dizaines | unités |
| ① | ||
| ⑥ | ||
| ⑤ |
Comme on ne change pas un nombre par des déplacements verticaux de jetons dans une même colonne, on peut reconnaître le produit comme
| centaines | dizaines | unités |
| ① | ⑤ | ⑥ |
soit « une centaine, cinq dizaines et six unités » qui se résume en « cent cinquante six ».
On remarque que l’abaque de Gerbert ne nécessite pas l’utilisation du chiffre zéro, ni de retenir les retenues.
On remarque également que, puisqu’on ne retient pas les retenues, on peut effectuer les multiplications partielles dans l’ordre qu’on veut, du moment qu’il y a les 4 produits partiels. D’ailleurs commencer par les produits les plus grands, permet de rapidement se faire une idée de l’ordre de grandeur du résultat : on voit dès le début que le produit fait « cent et quelques ».
Par contre, il est nécessaire de commencer par les produits les plus petits (ou par la droite) si on veut effectuer une multiplication posée :
| centaines | dizaines | unités |
| ⑥ | ||
| ③ | ||
| ② | ||
| ① |
Ensuite on peut résumer
- « trois fois deux égale six et trois fois dix égalent trente » en « trois fois douze égalent trente-six », et
- « dix fois deux égalent vingt et dix fois dix égalent cent », en « dix fois douze égalent cent vingt » :
| centaines | dizaines | unités |
| ③ | ⑥ | |
| ① | ② |
qui ramène à la multiplication posée :
Remarques
Si on utilise les grands carreaux comme séparateurs, on n’a pas besoin du chiffre zéro. C’est seulement si on veut en faire abstraction, qu’on doit l’écrire :
Passer des unités aux dizaines, revient à décaler d’un cran vers la droite, ce qu’on peut faire avec deux doigts seulement avec la méthode de Gerbert : on met un doigt sur chaque jeton et on décale les deux jetons en même temps, ce qui fait passer de
| centaines | dizaines | unités |
| ① | ② |
à
| centaines | dizaines | unités |
| ① | ② |
Adélard de Bath utilisait les parties externes de l’abaque de Gerbert pour poser les opérandes et n’effectuait les opérations qu’à l’intérieur de l’abaque :
| centaines | dizaines | unités |
| 1 | 2 | |
| ----- | ----- | ----- |
| ① | ||
| ⑥ | ||
| ② | ||
| ③ | ||
| ----- | ----- | ----- |
| 1 | 3 |
pour finir par
| centaines | dizaines | unités |
| 1 | 2 | |
| ----- | ----- | ----- |
| ① | ⑤ | ⑥ |
| ----- | ----- | ----- |
| 1 | 3 |
En effet, les calculs intermédiaires n’ont pas à être posés, on ne fait que des simplifications par échanges de jetons.
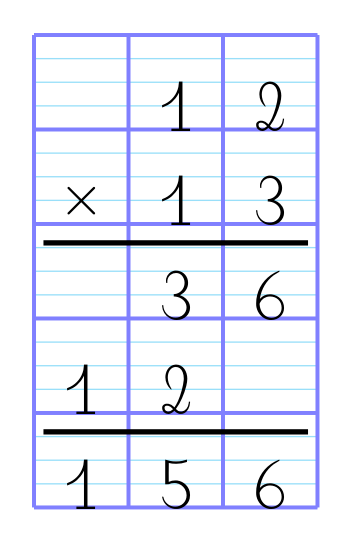
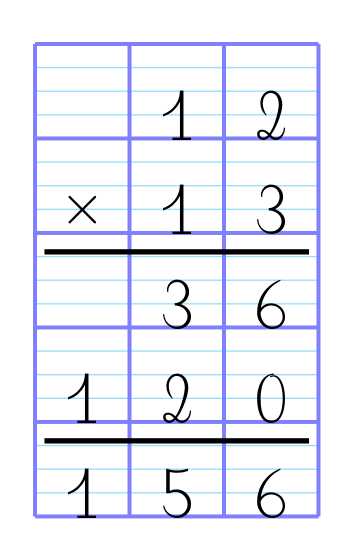
Commentaires