Sans avoir lu les écrits d’Euclide ni ceux d’Ératosthène, il paraît évident que ces deux-là connaissaient et pratiquaient la méthode algorithmique, au sens d’une séquence d’instructions (donc énoncées à l’impératif) :

• Lorsque Euclide calculait un pgcd, c’était par une suite de soustractions successives ;
• Le crible d’Ératosthène se construit étape après étape.

Chez Al-Khawarizmi, les méthodes exposées pour résoudre des équations utilisent des étapes qui doivent être parcourues dans l’ordre si on veut aboutir à la solution.

Chez Descartes, dans le discours de la méthode, on trouve cette description de l’algorithmique (sans le dire) :

diviser chacune des difficultés que j’examinerais, en autant de parcelles qu’il se pourrait, et qu’il serait requis pour les mieux résoudre.

La première informaticienne, Ada Lovelace, proposait un algorithme de calcul des nombres de Bernoulli. Il est vraisemblable que cet algorithme fonctionnait en séquence tout simplement parce qu’il était destiné à la machine analytique de Charles Babbage, laquelle utilisait des cycles comme la mise en mémoire de résultats intermédiaires et la récupération ultérieure de ces résultats.

Le tout premier ordinateur, ENIAC, était financé par un projet parallèle au projet Manhattan, auquel participait John von Neumann. L’architecture proposée par celui-ci est de très loin la plus répandue dans les ordinateurs, or elle impose la démarche algorithmique. D’où l’idée selon laquelle programmer un ordinateur, ça commence par l’algorithmique.

Mais ce n’est pas toujours vrai : Le calcul parallèle est à peu près incompatible avec l’algorithmique, ainsi que l’informatique quantique, et les processseurs vectoriels (utilisés dans les superordinateurs) rend celle-ci désuète. Or le succès grandissant des ordinateurs bi-cœurs et du calcul par réseau mettent le calcul parallèle de plus en plus à la mode.

Dans l’exemple du calcul de la moyenne de 100 nombres aléatoires, la démarche algorithmique (pour la somme des 100 nombres) consiste à effectuer dans l’ordre les opérations suivantes :

1. Créer une variable numérique qui contiendra la somme ;
2. Initialiser cette variable à 0 ;
3. Répéter 100 fois le point suivant :
4. Ajouter à la variable en question, un nombre pseudo-aléatoire entre 0 et 1 ;
5. Une fois qu’on a fini, diviser la somme des 100 nombres par 100.

En JavaScript (sous CaRMetal) cela donne ceci :

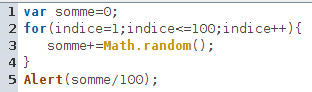
C’est la syntaxe de la boucle qui est complexe en JavaScript...

Et en Python (sous eric4) :

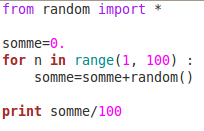
On remarque qu’il a fallu initialiser la variable somme à « 0. » au lieu de « 0 » pour que Python la considère comme réelle et non entière. On remarque également la simplicité de la boucle sous Python, « range(1,100) » désignant une liste d’entiers, comme dans l’onglet « calcul vectoriel ».

Or pour beaucoup d’élèves de Seconde,

• penser à créer une variable,
• penser que pour additionner 100 nombres, il faut additionner les deux premiers d’entre eux, puis additionner le troisième à la somme partielle, etc.
• Passer de cette constatation à la réalisation sur machine,

ce n’est pas facile du tout !

On peut dire que la démarche algorithmique n’est pas naturelle pour un élève entrant en Seconde. D’où l’intérêt de se poser la question de la pertinence de ladite démarche, et de la nécessité de la pratiquer ou la faire pratiquer.

Pour finir cet onglet, je cite Guillaume Connan (article pour Repères) :

Il faut donc être extrêmement attentif à la chronologie des instructions données. C’est un exercice intéressant en soi mais pas
sans danger (c’est d’ailleurs la source de la plupart des « bugs » en informatique).

Le même algorithme en Xlogo est plus simple à écrire, et à lire, parce que la boucle est effectuée sans faire référence à son indice, donc de façon statique : On répète 100 fois l’addition, sans avoir à imaginer la valeur que prend l’indice à chacune des répétitions :

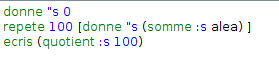
LOGO, comme LISP, OCamL, Haskell etc. est un langage fonctionnel, où la notion d’affectation est superflue, et la « programmation » entièrement basée sur la récursivité. Disons qu’en programmation fonctionnelle [1], au lieu de dire ce que doit faire la machine, on lui décrit la situation, et on la laisse se débrouiller pour trouver la réponse à partir de cette description. Cette façon de programmer permet donc de se passer de la démarche algorithmique. La version programmation déclarative de l’algorithme d’Euclide donne quelque chose comme ceci :

Le pgcd de a et b est égal au pgcd de a et a-b.

On n’y voit aucune affectation, aucune chronologie, et pourtant traduit en JavaScript on a bien un programme (extrait de cet article) :

Voici comment OcamL Light calcule la moyenne de 100 nombres aléatoires :

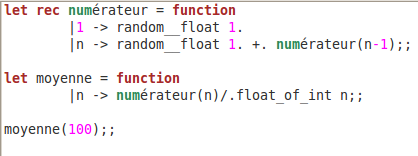
Alors, vaut-il la peine de contourner la difficulté que présente pour certains élèves la démarche algorithmique, et contourner la démarche elle-même en utilisant un langage fonctionnel ? Là encore je cite Guillaume Connan :

Cependant, utiliser des algorithmes récursifs nécessite de maîtriser un tant soit peu... l’axiome de récurrence. Or cette étude a été réservée jusqu’à maintenant aux seuls élèves de Terminale S. L’étude des suites débute depuis de nombreuses années en Première et chaque professeur a fait l’expérience des difficultés des élèves à maîtriser cette notion.

Rajoutons qu’en évoquant la récursivité, et en n’évoquant pas l’affectation de variables, on se met totalement en porte-à-faux par rapport aux impératifs du programme...

Ceci dit, même si la quasi-totalité des logiciels connus sont conçus avec des langages impératifs, donc grâce à l’algorithmique, quelques grandes créations logicielles ont été faites avec des langages fonctionnels :

• Les éditeurs de texte emacs et TeXmacs sont écrits en Scheme qui est une variante de LISP, donc fonctionnelle dans son principe.
• Il en est de même de plusieurs logiciels de calcul formel, notamment Yacas, Derive et Maxima.
• Le logiciel de démonstrations automatiques Coq et son interface CoqIde sont écrits en OCamL.

Sans aller jusqu’à la récursivité, on peut rendre les boucles statiques en utilisant des listes ordonnées (appelées vecteurs) ce qui contourne aussi la difficulté. Par exemple en SciLab, la boucle se rédige

for i=1:100

La notation « 1:100 » désigne la liste des 100 premiers entiers dans un logiciel de calcul matriciel tel que MatLab, Octave, SciLab ou Euler Math Toolbox (le double-point se lit « jusque »). On a donc un indice dans un tableau de nombres : Les 100 valeurs n’apparaissent pas à des moments successifs, mais sont stockées une fois pour toutes à différents emplacements d’un même tableau.

Mais avec SciLab il n’est même plus nécessaire d’écrire la boucle, on peut directement travailler sur le tableau ! Ci-dessous, le tableau des 100 nombres aléatoires est stocké dans la variable a, et la somme des éléments de a s’obtient par sum(a) :

Comme le montre la dernière ligne SciLab ci-dessus, on n’a même pas besoin de calculer la somme et la diviser par 100, puisque SciLab permet également de calculer directement la moyenne par mean.

Le calcul par un processeur vectoriel comme on en trouve dans les superordinateurs fonctionne de cette manière : Au lieu d’opérer sur des nombres, ils opèrent sur des vecteurs c’est-à-dire des tableaux de nombres.

Mais SciLab n’est pas le seul outil qui permet de calculer d’un coup une moyenne de 100 nombres : Les tableurs ont plus ou moins spécialement été conçus pour ça :

1. On entre dans la cellule A1 la formule « =ALEA() » ;
2. On la copie vers le bas, jusqu’à A100 ;
3. On sélectionne une cellule vide, dans laquelle on entre la fonction « =MOYENNE(A1:A100) »

Certes il y a bien eu une itération là-dedans, mais c’est le tableur qui s’en est chargé. L’élève qui manipule le tableur ne voit pas l’itération, et ne suit pas une démarche algorithmique...

Il en est de même pour la calculatrice graphique : Pour une Ti, on peut entrer

$Seq(random(),i,1,100) \rightarrow L1$

Ensuite, bien qu’on puisse écrire un programme pour calculer la moyenne des nombres stockés dans L1, il suffit d’aller dans le menu statistiques, et de choisir « calc » puis « 1-Var stat » pour avoir l’affichage de la moyenne (avec en bonus les quartiles) : Là encore, c’est la calculatrice qui se charge du travail...

Certes, les élèves les plus curieux (et passionnés) adoreront qu’on leur explique comment leur calculatrice calcule une moyenne, mais les autres (et ils risquent d’être nombreux) vont dire « à quoi bon se fouler alors que de toute façon la calculatrice le fait ? »

Dans ce cadre, la pertinence de la démarche algorithmique peut se comparer à l’opinion d’une large proportion de conducteurs qui ne jugent pas utile d’être des experts de la mécanique pour piloter leur voiture !

Depuis que la vitesse des processeurs plafonne à 2 GHz, pour construire des ordinateurs plus rapides, on met plusieurs « cœurs » dans les processeurs (on n’a d’ailleurs pas attendu de dépasser le GHz pour cela). Ce qui mine de rien remet au goût du jour le calcul parallèle, rival de l’architecture de Von Neumann qui incarne aujourd’hui la démarche algorithmique. Et même avec un processeur unique, la programmation événementielle sort du contexte temporel qui préside à la démarche algorithmique puisqu’on attend un évènement pour lancer le processus auquel il doit répondre.

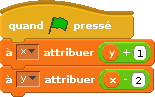
Or dès lors qu’il y a deux processeurs à travailler en même temps sur des variables communes, il y a des risques de conflit, comme le montre l’exemple suivant en Scratch (langage spécialisé dans le calcul parallèle) :

La scène comprend deux lutins, des robots, appelé Rôôô et Beau (évidemment). Le programme de Rôôô est celui-ci :

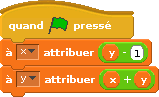
et celui de Beau celui-ci :

Bien malin qui saura deviner la valeur de x après le clic sur le drapeau vert ! En effet tandis que Rôôô essaye de forcer la valeur de x à être égale à 2, Beau essaye en même temps de forcer la même valeur à être égale à 3. Le pauvre x en est tout écartelé !

Exercice

Avec deux variables x et y, et le programme de Rôôô suivant :

et le programme de Beau que voici :

Deviner les valeurs que prennent x et y après le clic sur le drapeau !

Ce genre de conflit (presque complètement en dehors du champ de l’algorithmique) n’a rien de théorique, puisque l’article sur Descartes cité précédemment fait l’objet en ce moment d’un blocage dû à une écriture en commun par des auteurs qui ne sont pas d’accord entre eux sur le contenu de ce qu’ils écrivent :

À noter que pour résoudre ce conflit, le site wikipedia utilise bel et bien le langage de l’algorithmique :

En fait, l’étude des processeurs concurrents se fait par des outils très différents de l’algorithmique, surtout lorsqu’il y a beaucoup de processeurs, comme dans les réseaux de neurones. Dans ce cas l’outil mathématique le plus approprié semble être les automates cellulaires. On peut considérer que dans un de ces superordinateurs à multiprocesseurs, au lieu de partager le travail dans le temps comme le fait l’algorithmique, on le partage dans l’espace, entre les processeurs. Or l’espace a plus de dimensions que le temps (typiquement, 4 dans les cablages optimaux entre processeurs).

Deux exemples de ces superordinateurs distribués :

Le projet SETI, au but un peu original...

Plus mathématique (arithmétique pour être précis), le GIMPS...

Et, avec moins de postes en réseau local, le rendu du film Shrek 3 aurait pris des décennies s’il n’avait pas été fait en calcul massivement parallèle...