À l’ouverture du logiciel, la fenêtre qui s’ouvre est assez classique dans son aspect, et permet assez vite de construire des figures dynamiques : On est en terrain connu :

• L’outil « line » est étrange, car il construit bien une droite mais ne dessine qu’un segment. Ce peut être un avantage pour les exercices sur les coordonnées, les droites parallèles aux axes de coordonnées étant tracées juste dans la partie intéressante (le tracé s’arrête au point d’intersection).
• Il y a deux icônes pour les perpendiculaires, en effet la première construit la droite (en dessinant un segment) et la seconde construit le projeté orthogonal.
• Les angles sont en degrés, mais orientés (l’icône comprend une flèche).
• L’outil « symétrique » sert à la fois pour les réflexions et les symétries centrales, malgré ce que laisse penser l’aspect de son icône.

La figure ci-dessus (à droite) montre le début de la construction d’un hexagone régulier. On constate que par défaut, le point d’intersection (GeX laisse choisir parmi les deux points) est représenté dans une couleur différente des points libres. Le nommage des points est automatique, mais on peut les renommer.

Mais le plus original avec ce logiciel de géométrie dynamique, c’est la possibilité non seulement de vérifier une conjecture (est-ce que l’hexagone est vraiment régulier) mais le cas échéant, d’en obtenir une démonstration.

Pour vérifier une conjecture, on clique en haut de la figure sur "prove" et là, on choisit "to prove", ce qui permet de choisir la conjecture (par exemple, entrer les noms des trois points dont on souhaite prouver qu’ils sont alignés).

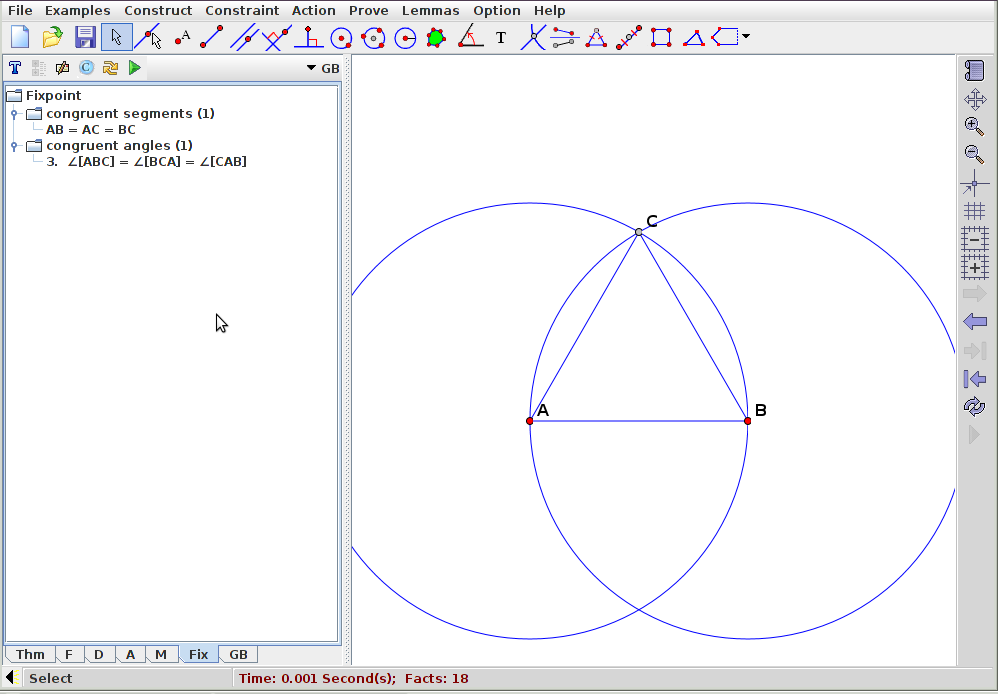
Constatant que parmi les propriétés qu’on peut conjecturer, il n’y en a aucune sur la nature d’un hexagone, on essaye à défaut de prouver que le triangle $ABC$ est équilatéral. C’est là qu’intervient le cadre de gauche dans la figure ci-dessus : On y apprend l’historique de la construction et la propriété à démontrer : Que $ABC$ est équilatéral. Tout impatient, on clique alors sur le triangle vert pour obtenir la démonstration, et on a ceci :

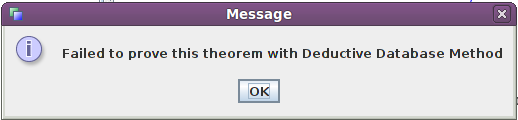
Morale : Gex est capable de faire des démonstrations mais pas toujours... Pour essayer d’en savoir plus, on peut voir s’il est possible de choisir une autre méthode de démonstration. On peut, et les méthodes de calcul formel confirment que le triangle est bien équilatéral (voir l’onglet "centre de gravité" pour voir ce qu’elles produisent). D’ailleurs, Gex "sait" que le triangle est équilatéral puisque si on demande l’affichage des "points fixes" de la base de données (onglet "Fix" en bas), on aperçoit que l’égalité des trois longueurs et l’égalité des trois angles sont apparues dans la base de données. Il s’agit peut-être d’un bogue, le logiciel étant encore en cours d’élaboration.

Dans la figure ci-dessous, il s’agit de démontrer que $(AB)\bot(FG)$ :

Les méthodes de calcul formel permettent de le faire en calculant un produit scalaire, mais cette fois-ci la méthode déductive fonctionne, en produisant une stratégie de démonstration, dont voici le début :

La traduction en termes de stratégie de résolution commence par quelque chose comme ceci :

Je pourrais démontrer que (FG) est perpendiculaire à (AB) si je savais démontrer que (2) l’angle entre (FG) et (AB) est égal à l’angle entre (BE) et (AE) et (3) que (BE) est perpendiculaire à (AE) ;

Je vais donc transformer l’exercice difficile « montrer que (FG) est perpendiculaire à (AB) » en deux exercices plus simples :

2 : Montrer que l’angle entre (FG) et (AB) est égal à l’angle entre (BE) et (AE) ;

3 : Montrer par ailleurs que (BE) est perpendiculaire à (AE) ;

Et je répète la même stratégie pour chacun de ces deux exercices.

La fin de la stratégie mène alors à des démonstrations d’évidences (axiomes ou hypothèses) :

Pour rédiger cette démonstration, il vaut mieux donc la lire de bas en haut, c’est-à-dire en commençant par la fin :

• (13) Le triangle ABD est inscrit dans un demi-cercle, donc rectangle en D ;
• (12) Autrement dit, le triangle DFG est rectangle en D ;
• (11) De même, le triangle EFG est rectangle en E ;
• (9) Les quatre points D, E, F et G sont donc cocycliques.
• (8) D’après le théorème de l’angle inscrit (dans le cercle de centre $C$), $\widehat{EAB}=\widehat{EDB}$ ;
• (7) Mais $\widehat{EFG}$ est aussi égal à $\widehat{EDB}$, d’après le théorème de l’angle inscrit dans le cercle passant par D, E, F et G ;
• (5) Par conséquent, $\widehat{EFG}=\widehat{EAB}$
• (3) Donc l’angle entre (FG) et (AB) est égal à $\widehat{BEA}$ (ce point mériterait d’être un peu précisé...)
• (2) Or le triangle BEA est inscrit dans un demi-cercle, donc il est rectangle en E ;
• (1) Donc $(FG)\bot(AB)$ cqfd.

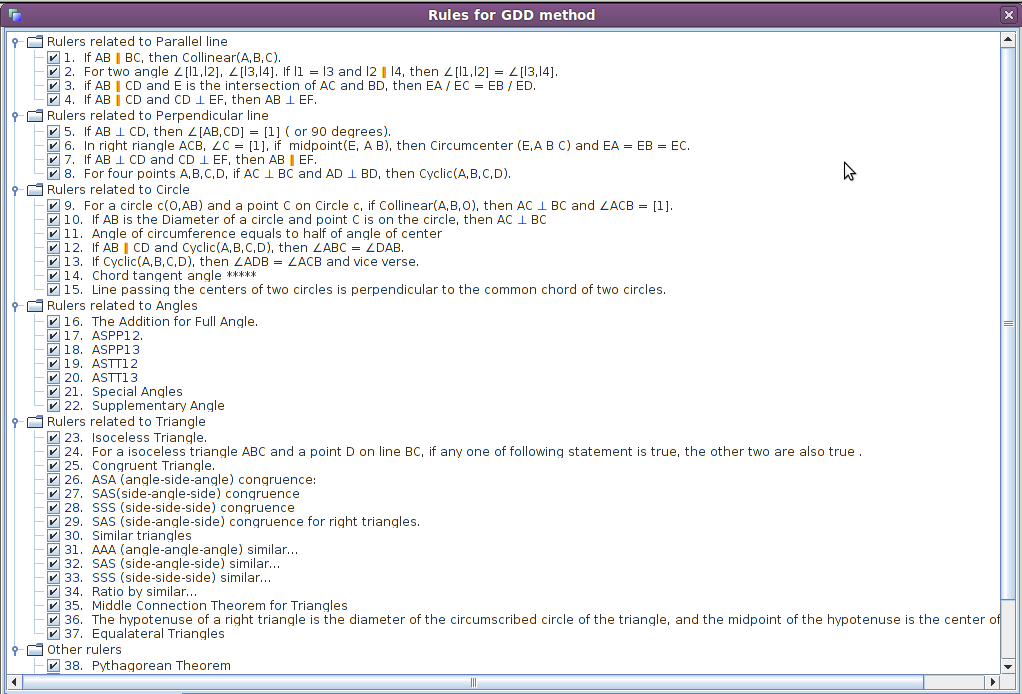
Parfois une justification est donnée sous la forme « rule 10 » mais pour connaître l’axiome utilisé, il faut une liste de ceux-ci, on l’obtient en cliquant sur « Lemmas » en haut de la fenêtre, ce qui donne cet affichage :

Quoique juste, la démonstration ci-dessus demande à être comparée avec celle d’un élève (de Seconde), que voici :

On cherche à prouver que [AN], [BM] et (PO) sont les hauteurs du triangle ABP. ABM et ABN sont inscrits dans un cercle de Thalès. Le théorème de Thalès selon les Allemands et Anglo-saxons énonce : « un angle inscrit dans un demi-cercle est droit ». En conséquence, [BM] est perpendiculaire à [AP) et [AN] est perpendiculaire à [BP). Ainsi, O est l’intersection de [AN] et [BM], et par conséquent l’orthocentre, car l’on sait désormais que [AN] et [MB] sont des hauteurs. La droite (OP) passe par P (sommet du triangle) et O (orthocentre). De ce fait, l’on peut affirmer que (OP) est une hauteur du triangle ABP et donc, dans le même principe, affirmer que (OP) est perpendiculaire à [AB].

C’est quand même mieux, non ? En fait la propriété « droites concourantes » ne semble pas exister sous Gex, comme le montre l’onglet suivant.

Gex peut-il démontrer des propriétés aussi classiques que la concourance des droites remarquables du triangle ? Pour le savoir, on doit construire deux de ces droites, puis leur intersection, et enfin montrer que la troisième droite remarquable passe aussi par ce point. En effet, si Gex ne sait pas démontrer que trois droites sont concourantes, il sait démontrer que trois points sont alignés.

Voici donc la construction, exportée par Gex en une figure animée :

Il s’agit de prouver que A, G et E sont alignés, G ayant bien entendu été défini comme intersection des médianes (BF) et (AE).

Seulement la méthode consistant à demander à Gex de prouver cet alignement donne le message d’erreur que voici :

C’est d’autant plus décevant que la consultation des « points fixes » de la base de données construite pendant la tentative de démonstration donne des renseignements intéressants sur les rapports de longueur :

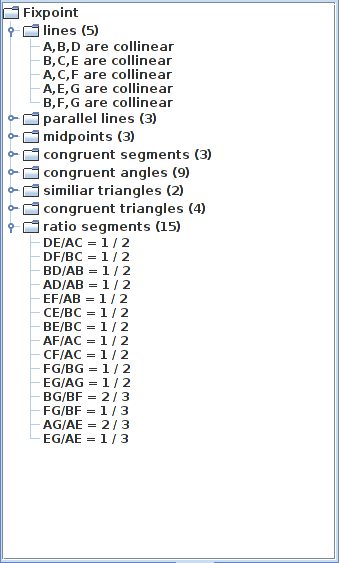
Et en plus, le centre de gravité est un objet connu de Gex (dans l’entrée « construct » du menu). Et bien la méthode par calcul formel permet bien de démontrer l’alignement. Pour la mettre en route, on simplifie un peu la figure, en utilisant la construction directe du centre de gravité :

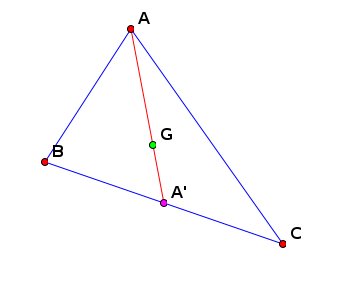
Il s’agit maintenant de démontrer l’alignement de A, G et A’ (ce dernier ayant été défini comme milieu de (BC]). Là encore, la déduction ne marche pas (du moins sans construction auxiliaire comme les droites du milieu) mais la méthode des bases de Göbner donne ceci :

Voici les étapes du raisonnement :

• On commence par choisir un repère orthonormé (au cas où il y aurait des cercles) d’origine A et tel que B est sur l’axe des abscisses. On nomme alors les coordonnées des différents points de la figure, ce qui donne 7 variables.
• On traduit par des équations polynomiales entre ces variables, les données de l’énoncé. Avec les deux coordonnées de G et celles de A’, cela donne 4 équations à 7 inconnues.
• On écrit le système formé par ces équations ;
• On rajoute sous une forme analogue la propriété à prouver (ici un déterminant nul)
• On réduit (par des calculs non affichés) ; on trouve 0 ce qui veut dire que la condition x7x10=x8x9 est conséquence des hypothèses : L’alignement est vérifié.

En résumé, cette méthode est correcte mais basée (c’est le cas de le dire) sur la géométrie repérée, et l’intervention de la logique est beaucoup moins abondante que dans la méthode par déduction.

Un outil analogue est xcas qui marie calcul formel et géométrie dynamique. Sauf que le moteur de calcul tend à rendre les mouvements de la figure quelque peu saccadés, et que finalement la géométrie d’xcas n’est pas si dynamique que ça.