Nous connaissons le plus souvent, de par notre cursus universitaire, essentiellement la géométrie affine, généralement construite à partir des structures vectorielles, et les géométries issues des formes bilinéaires, comme la géométrie euclidienne. Il en résulte que nos raisonnement géométriques sont formatés soit par l’affine, soit par l’euclidien, ce qui est de toute façon suffisant puisque nous n’avons à travailler, dans nos classes, que dans ces environnements là.
Cet article vous propose une petite excursion dans le monde hyperbolique, qui reste un monde encore assez proche du nôtre (l’euclidien) pour y apprendre deux choses :
– comment les notions usuelles que l’on connait peuvent s’étendre naturellement à une géométrie neutre, plus englobante, et en même temps,
– comment peut être perçu par un élève l’enseignement de la géométrie quand il commence à entrer dans le monde hypothético-déductif, qui plus est dans un certain flou axiomatique qui justifie que les demandes de précision dans les démonstrations soient cantonnées à quelques thèmes précis.
En effet, l’approche qui va en être faite se calque, d’une certaine façon, sur la démarche utilisée au collège pour présenter la géométrie : nous allons travailler dans un modèle de cette géométrie, avec les outils usuels de la géométrie (droite équerre compas) et nous allons explorer cette géométrie comme on le fait de la classe de 6° à la classe de 4°. Puis nous donnerons quelques définitions précises et nous démontrerons quelques théorèmes.
Chacun comprendra bien que nous n’aurons alors pas toujours véritablement étudié en soi la géométrie hyperbolique mais parfois cette géométrie dans un modèle, c’est-à-dire en utilisant fortement les images et les représentations dans un modèle des objets mathématiques que l’on va manipuler puis définir. C’est ce qui se passe en classe : nous identifions en permanence nos supports (papier, tableau, écran d’ordinateur, TNI qui sont autant de modèles de la géométrie euclidienne plane, à la géométrie plane elle-même. Et parfois, ou souvent selon les classes, la place du perceptif - c’est-à-dire du modèle - peut être mathématiquement ambigu.
De même que les élèves ont des outils physiques pour construire dans le modèle de la feuille de papier des dessins géométriques qui représentent des figures mathématiques, nous disposons de divers outils du modèle. Comme pour la géométrie dynamique euclidienne, nous disposons naturellement de plus d’outils que dans le contexte du monde sensible. Ainsi aux droites, segments, perpendiculaire, compas, symétrie axiale (qui est toujours un pliage) usuels, nous ajoutons les outils de milieu, médiatrice, bissectrice etc ...
Toutefois, comme ce texte s’adresse à des enseignants de mathématiques - donc des esprits soucieux d’une présentation théorique claire - le premier onglet donne les principales définitions qui permettent de poursuivre en même temps que l’exploration « scolaire », une démarche plus théorique.
Organisation de l’article
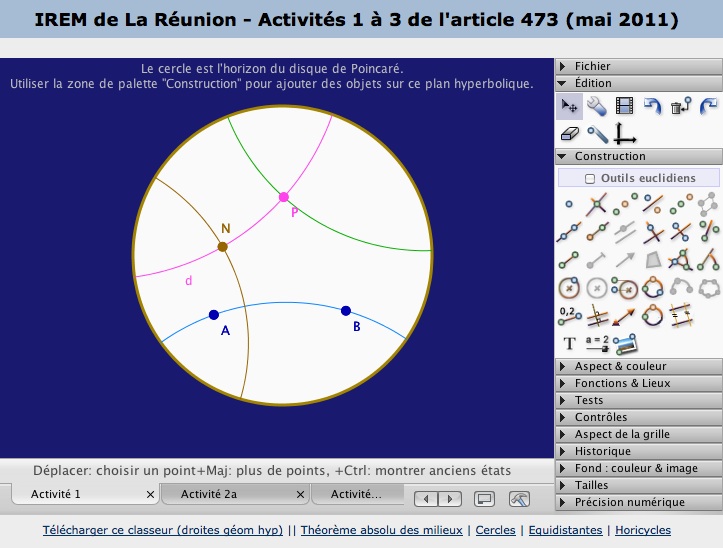
Il se décline donc à plusieurs niveaux de lecture, selon l’intérêt que chacun porte à ce thème. Si on veut se placer réellement dans une situation d’homologie didactique, c’est-à-dire se plonger dans une exploration de la géométrie hyperbolique comme on le ferait en formation initiale ou dans un stage de formation continue, on téléchargera la fiche en fin d’article, et on fera les activités proposées directement avec la version 3.6 de CaRMetal. La fiche d’activités est construite avec des phases d’institutionnalisation de telle manière que l’on puisse la travailler seul tout en ayant un certain recul par rapport à ce que l’on fait.
Si on veut avoir un aperçu de la géométrie hyperbolique plus rapidement, on peut choisir d’utiliser la fiche tout en manipulant les figures déjà faites directement en ligne à cette page (pour les personnes qui ne connaissent pas le logiciel - à ouvrir soi-même dans un nouvel onglet), ou en téléchargeant les classeurs en fin d’article.
L’article est surtout fait pour deux types de lecteurs :
• celui qui souhaite un parcours guidé rapide, sans chercher à manipuler lui-même dans un premier temps, ou est simplement curieux de cette nouveauté du logiciel.
• le spécialiste de la formation qui peut voir là un nouveau champ d’activités, pour qui des travaux d’étudiants en situation, sont disponibles dans le corps du texte.
Dans les trois onglets des premières activités, en effet, on trouvera généralement dans des blocs repliés pour ne pas alourdir la lectures des autres, des productions d’étudiants effectuées depuis plusieurs années, soit sur Cabri-Géomètre soit sur CaRMetal. En effet ces logiciels étant des micro-mondes, il est élémentaire de leur ajouter toutes sortes de fonctionnalités. La nouveauté de la version 3.6 est que ceci soit installé au sein du logiciel avec une souplesse d’utilisation surprenante. Ces fonctionnalités sont complétées de l’ajout de nombreuses commandes hyperboliques en javascript pour faire des scripts hyperboliques. Nous consacrerons ultérieurement un article dédié aux pavages hyperboliques dynamiques, réalisés par des scripts de CaRMetal.
Avertissement
Cet article a été rédigé pour les versions 3.6 ou 3.6.2 de CaRMetal.
Depuis la version 3.6.5, la palette de construction a été complétée (grands remerciements à l’auteur) d’une ligne supplémentaire qui propose 6 nouveaux outils hyperboliques spécifiques aux pinceaux de droites, qui seront étudiés dans un second article.
Les copies d’écran de la palette de construction ne correspond donc pas exactement à celle des versions 3.6.5 et ultérieures.
Présentation
Introduction générale
On s’intéresse à une géométrie dans laquelle le V° postulat d’Euclide (par un point il passe une et une seule parallèle à une droite donnée) n’est pas vrai, au sens où il peut y avoir plusieurs parallèles à une droite donnée, et pour laquelle toutes les autres « demandes » initiales (les postulats et demandes d’Euclide, ou les axiomes de Hilbert) sont vérifiés.
En pratique on est donc sur une géométrie réelle, c’est-à-dire sur R, un corps archimédien - c’était déjà une demande d’Euclide - avec les axiomes de continuité qui conviennent (explicites chez Hilbert, bien entendu implicites chez Euclide). En particulier il y a un bijection entre chaque droite hyperbolique et la droite réelle, et le plan est métrique, on dispose d’une distance si on le souhaite. Ce n’est pas nécessaire pour la découverte de la géométrie, ni même son exploration poussée (en particulier parce que l’on est dans un modèle), mais c’est indispensable pour certaines constructions bien spécifiques comme les pavages par exemple.
Il est bien connu que dans le traité d’Euclide, la première fois que l’on a besoin de l’axiome des parallèles intervient à la proposition 31 et donc que toutes les précédentes sont vraies (note 1) dans une géométrie dite depuis « géométrie neutre » dans laquelle cet axiome n’est pas encore utilisé. La géométrie neutre contient donc la géométrie euclidienne et la géométrie hyperbolique, mais pas la géométrie elliptique qui ne vérifie pas les propriétés d’Euclide dès la propriété 7, qui veut que l’intersection de deux cercles contienne au plus deux points (il peut y en avoir 4 dans certaines situations elliptiques).
Une approche classique consiste à prendre les axiomes de Hilbert sauf celui des parallèles et reconstruire une géométrie plane neutre, dite « Plan de Hilbert » (livre en ligne choisir la page 96) par Robin Hartshorne, montrer toutes les propriétés usuelles de cette géométrie avant d’ajouter un axiome pour la géométrie euclidienne ou un pour la géométrie hyperbolique.
Voici sa version, toute proche, Jacqueline Lelong Ferrand, dans son ouvrage « fondements de la géométrie » (1985), reprend les groupes d’axiomes comme Hilbert, ma is centre ces derniers axiomes sur l’existence d’un pliage :
Les axiomes de géométrie absolue
(version de Jacqueline Lelong Ferrand)
Il s’agit d’un ensemble d’axiomes pour aller très vite vers une géométrie absolue réelle : contrairement à la démarche de Hilbert, qui voulait reconstruire R, ici le corps des réels est supposé déjà construit.
Plan Métrique
Un ensemble P est dit un plan métrique, s’il vérifie les quatre groupes d’axiomes suivant. Ces axiomes définissent une géométrie neutre. Un plan métrique sera euclidien ou non euclidien s’il vérifie de plus l’axiome d’Euclide, ou pas.
I. Les axiomes d’incidence
Les éléments du plan P sont appelés points, et dont certaines parties, appelées droites, vérifient les axiomes suivant :
I.a. Par deux points il passe une unique droite.
I.b. Chaque droite contient au moins deux points.
I.c. Il existe trois points non alignés.
On notera que l’incidence n’est pas définie, elle est implicitement l’appartenance du point à la droite.
II. Les axiomes d’ordre
II.a. Chaque droite du plan contient deux relations d’ordre total, opposées l’une de l’autre.
En fait cet axiome est une façon concise de déterminer une relation « entre », et donc les segments et les demi-droites. Les segments étant définis, on a alors besoin de l’axiome de Pasch sur les triangles :
II.b. Si une droite rencontre un des côtés d’un triangle (en dehors d’un sommet), elle rencontre alors un autre côté du triangle.
III. Les axiomes de distance
On suppose qu’il existe une application d : PxP → R+, appelée distance, telle que :
III.a. Pour tous points du plan A et B, d(A,B) = d(B, A)
III.b. d(A,B)=0 si et seulement si A=B
III.c. Pour qu’un point C de la droite (AB) appartienne au segment [AB] il faut et il suffit que d(A, C) + d(C, B) = d(A, B)
III.d. Pour toute demi-droite [Ou) d’origine O et pour tout réel x>0, il existe un point M de [Ou) tel que d(O, M) = x.
Ce point M est unique d’après les axiomes précédents. Les lecteurs curieux pourront faire le lien avec les axiomes de Hilbert sur la congruence des segments.
Dans son ouvrage, J. L-F. précise que la distance d(A,B) s’appelle la longueur de [AB] et est notée AB. C’est un abus de langage car il s’agit de la mesure de la longueur. En général les grandeurs sont définies indépendamment d’une mesure associée.
IV. Les axiomes de pliage
C’est ici que réside l’originalité de la démarche retenue par Jacqueline Lelong-Ferrand : utiliser désormais des axiomes sur les isométries plutôt que des axiomes de congruence sur les angles et les angles et segments comme Hilbert.
Définition : on appellera automorphisme du plan P, toute bijection de P sur P qui conserve les distances et transforme les droites en droite.
IV.a. Pour toute droite d du plan P, il existe un unique automorphisme autre que l’identité laissant fixe chaque point de d.
Cet automorphisme est appelé symétrie d’axe d, noté $s_d$.
IV.b. Étant données deux demi-droites de même origine [Ox) et [Oy), il existe au moins une symétrie orthogonale $s_d$ telle que $s_d$([Ox)) = [Oy).
On notera que contrairement à d’autres systèmes d’axiomes des plans métriques, même ceux utilisant les symétries orthogonales, ce système ne définit pas a priori l’orthogonalité et ne donne aucun axiome direct sur l’orthogonalité.
Avec ce système d’axiome, le fait que l’intersection de deux cercles soit au plus deux points est un résultat non trivial (alors que c’est la propriété 6 chez Euclide ... mais avec moins de précautions). On sait que c’est une propriété neutre (vraie en géométrie hyperbolique et euclidienne) mais pas absolue, ie pas vraie en géométrie elliptique où l’on peut avoir 4 points d’intersection.
Le modèle du disque de Poincaré
Quand on propose de définir une géométrie avec une axiomatique, on n’essaie plus de définir les objets premiers par eux même - on a compris que cela n’avait pas de sens - mais seulement leurs relations sous forme d’axiome. C’est ce qui a été fait dans l’exemple précédent : l’auteure n’essaie pas de définir ce qu’est une droite, mais définit seulement des relations ou des propriétés sur les points et les droites
On dit que l’on a une interprétation d’un système d’axiome quand on fait correspondre à ces objets premiers d’autres objets mathématiques connus, et cette interprétation est dite un modèle du système d’axiomes (ici de la géométrie hyperbolique) quand tous les axiomes sont vérifiés.
La géométrie hyperbolique a d’abord été construite de manière théorique, par Lobatchevky et Bolyai indépendamment l’un de l’autre vers 1829, en montrant que la non contradiction de cette nouvelle géométrie était équivalente à celle de la géométrie euclidienne. Il n’y avait aucun modèle - cela n’avait même pas de sens, d’où des notation parfois complexes et obscur de Bolyai par exemple. Cela n’a pas empêche ce dernier de montrer que la quadrature du cercle était réalisable dans cette nouvelle géométrie et d’en donner les constructions.
Un premier modèle réel d’une partie du plan hyperbolique a été mis en évidence par Beltrami, en 1868, par la géométrie intrinsèque de la pseudosphère (classeur de 26 figures dynamiques en ligne) puis Klein a tout de suite vu (1869), dans le travail de Beltrami un modèle du plan hyperbolique complet, dit depuis disque de Klein-Beltrami qui, pour la géométrie a l’avantage d’être projectif mais pour l’utilisateur l’inconvénient d’être non conforme.
Le modèle du disque de Poincaré est tout aussi facile à étudier que celui de Klein-Beltrami tout en ayant cet avantage d’être conforme, c’est-à-dire que les angles que l’on construit dans le modèle ont même mesure les angles de la géométrie.
Description du modèle du disque de Poincaré
Cette description n’est aucunement nécessaire pour la suite, et d’aucune aide pour comprendre ce que l’on va explorer, mais elle permet d’accompagner nos propres images mentales de la géométrie hyperbolique, en particulier pour les utilisateurs qui voudront faire d’autres macro constructions, même si ces images seront attachées - dans un premier temps - au modèle.
Le plan hyperbolique est l’intérieur d’un cercle, appelé alors horizon. Les points à l’intérieur sont les points du plan. Les points du cercle sont les points à l’infini du plan hyperbolique. On les appelle des points idéaux. Disposer des points idéaux simplifie grandement certaines constructions.
La droite (AB) est l’arc de cercle passant par A et B et orthogonal à l’horizon, c’est-à-dire dont les tangentes aux points d’intersection sont orthogonales. Il n’y a pas de barycentre en géométrie hyperbolique mais la question de l’ordre des points sur une droite est traité par les axiomes de Hilbert pour que l’ordre de R soit disponible sur chaque droite. Le segment [AB] de la droite (AB) ne pose donc pas de problème, c’est la partie entre A et B. C’est aussi l’intersection des demi-droites [AB) et [BA) comme dans le cas euclidien.
Dans le cas particulier où A et B sont alignés avec l’horizon, la droite hyperbolique (AB) devient le diamètre euclidien et le segment hyperbolique est le segment euclidien.
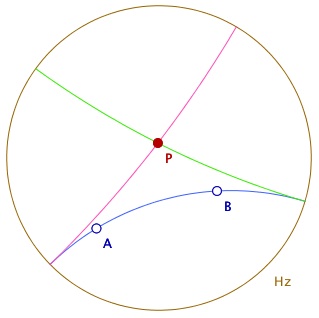
La symétrie orthogonale pour ce modèle est l’inversion euclidienne par rapport à l’arc de cercle. Historiquement c’est à cause des propriétés de l’inversion – et de son écriture complexe homographique - que Poincaré a découvert ce modèle.
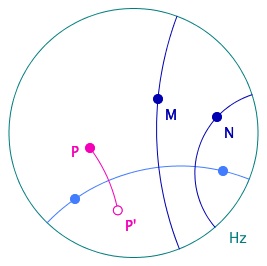
un point P et son symétrique P’
Le modèle est donc conforme, et en particulier l’orthogonalité est définie par les cercles orthogonaux : la perpendiculaire à (AB) en M est (la trace du) cercle passant par M, orthogonal à l’horizon – pour être une droite hyperbolique – et orthogonal au cercle support de la droite hyperbolique – pour lui être perpendiculaire. Elle se construit aussi sans difficulté par les inversions.
Puisqu’un modèle vérifie les axiomes de la géométrie dont il est une illustration, tout ce qui est vrai en géométrie hyperbolique, l’est aussi dans le modèle. Et réciproquement si une propriété est fausse dans le modèle, elle n’est pas une propriété hyperbolique. Par exemple pour vérifier que la droite d’Euler n’est pas une notion hyperbolique il suffit de vérifier que les trois points « O, G, H » ne sont pas alignés dans le disque de Poincaré.

Par contre, sur le plan théorique, une propriété vraie dans un modèle ne fait pas nécessairement une propriété hyperbolique alors que c’est essentiellement ce raisonnement que nous allons faire dans l’exploration de la géométrie hyperbolique. En pratique pour le cas hyperbolique, ce n’est pas un vrai problème, on ne fera qu’explorer des propriétés élémentaires de la géométrie. Mais dans le cas elliptique, si l’on n’est pas vigilant, il peut y avoir parfois des confusions, conceptuelles, entre la géométrie elliptique et la géométrie du modèle elliptique étudié.
Point de vue retenu pour cette présentation et vocabulaire induit
Dans les onglets suivants, on propose quelques activités pour faire découvrir la géométrie hyperbolique en formation initiale ou continue des enseignants, pouvant susciter une réflexion sur l’enseignement de la géométrie en collège. Il y a plusieurs façons de fixer le vocabulaire de la géométrie hyperbolique (en particulier autour du parallélisme). L’option retenue ici présente deux particularités. Elle a déjà l’avantage - pour une première grille de lecture - de coller aux pratiques géométriques des classes de collège - droites remarquables du triangles, symétries centrales et axiales.
Mais surtout, elle s’appuie sur une axiomatique pour les géométries non euclidiennes (GNE) dont on reparlera dans le second article, l’axiomatique de Bachmann (1959), construite sur les groupes de transformations et qui fait donc la part belle aux générateurs que sont les symétries axiales, puis aux symétries centrales. Cette axiomatique qui se veut très générale - les théorèmes sont montrés avant que l’on ne sépare les trois principales géométries - utilise la notion de pinceaux de droites (on peut aussi dire les faisceaux, mais une certaine tradition a conserver l’anglissisme issu du terme pencils dans les articles en anglais). Les pinceaux sont des familles de droites qui ont une propriété - éventuellement un élément - en commun.
En géométrie euclidienne il y a deux types de pinceaux :
• les pinceaux à centre - c’est-à-dire les pinceaux de droites concourantes
• les pinceaux à axe - c’est-à-dire les pinceaux de droites ayant une perpendiculaire commune.
Dans un contexte euclidien, on sait que ces derniers pinceaux correspondent aux droites parallèles et que s’il y a une perpendiculaire commune il y en a une infinité. Il en résulte / cela provient du fait (selon l’approche préliminaire) qu’il existe des translations et des rectangles.

avec les droites (AB), (CD), et la droite du pinceau passant par E
Le cas hyperbolique scinde les pinceaux euclidiens à axe en deux catégories : des pinceaux qu’on appellera toujours à axe, ce seront les droites qui ont une perpendiculaire commune, et un troisième type de pinceaux dont les droites n’ont ni point ni axe commun. Elles ont alors un autre objet en commun mais qui n’est pas à proprement parlé hyperbolique ; elles ont un même point idéal en commun, c’est-à-dire un même point à l’infini. On dira (avec Lobatchevsky) que ces droites sont parallèles. De ce point de vue, la géométrie euclidienne est une géométrie où les pinceaux à axe et les pinceaux de parallèles sont confondus.
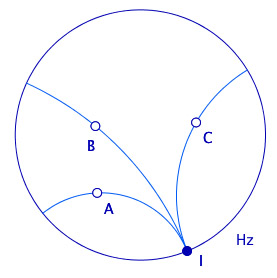
et de point idéal I
Dans l’autre sens, qui nous concerne plus pour la formation, on passe de la géométrie euclidienne à la géométrie hyperbolique en ajoutant un type de pinceaux de droites. Il va en résulter que les propriétés des droites remarquables du triangle vont évoluer. Elles étaient en pinceaux à centre (droites concourantes) elles vont toujours avoir une propriété remarquable, elles vont être en pinceaux, avec les trois types possibles.
Pour information, dans cette présentation, le passage de la géométrie euclidienne à la géométrie elliptique consiste au contraire en la fusion des deux types de pinceaux : les pinceaux à axes sont aussi à centre : les droites concourantes ont aussi une perpendiculaire commune. On imagine bien que cette fusion fait que pratiquement tout est possible en géométrie elliptique, mais ceci est une autre histoire qu’on n’abordera pas ici.
Pour revenir aux droites hyperboliques, deux droites pourront donc être :
• sécantes (un point commun)
• à axe (une perpendiculaire commune)
• parallèles (un point idéal commun)
Dans d’autres présentations les droites à axes sont parfois dites parallèles - et alors par un point il passe une infinité de parallèles), ou encore hyperparallèles. Le cas des droites parallèles est alors appelé « parallèles limites ».
Dans ce contexte, la difficulté d’une approche axiomatique de la géométrie hyperbolique est par exemple de montrer que si deux droites ne sont pas sécantes et n’ont pas de perpendiculaire commune alors elles ont ... un point idéal (non hyperbolique donc) en commun. Et dans des contextes plus généraux, on a des situations intermédiaires, où cette partition en trois types de couples de droites n’est pas vérifiée, et donc des géométries plus complexes (mais marginales) dites semi-hyperboliques.
Dans la présentation que nous allons proposer, on jouera sur les propriétés « naturelles » (intuitives) des pinceaux de droites - de droites remarquables d’un triangle - et en particulier que les trois types sont disjoints : si des droites sont en pinceau et que deux ont une perpendiculaire commune, alors le pinceau est à axe. C’est un des aspects qui permettra de faire le lien avec la présentation de la géométrie au collège.
Interface CaRMetal
Présentation de l’interface hyperbolique
Un nouveau mode est disponible dans la version 3.6 de CaRMetal, à savoir une figure hyperbolique dans le disque disque de Poincaré
Il ouvre une fenêtre avec un aspect nouveau :

et surtout une palette de construction, non pas nouvelle, mais modifiée, tout en gardant l’aspect conventionnel des icônes euclidiennes et sa possibilité d’utiliser les constructions euclidiennes dans le modèle hyperbolique :
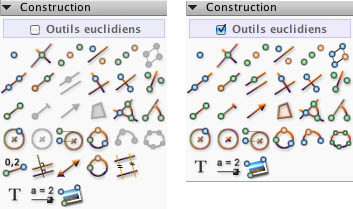
S’il faut présenter les outils de constructions d’un nouvel environnement, en particulier pour une utilisation optimisée et pertinente, dans le cadre d’une découverte de la géométrie hyperbolique, en formation, on se contentera de commenter seulement les trois premières lignes de la palette. De même si on veut jouer le jeu d’une découverte intuitive de la géométrie hyperbolique, sans a priori conceptuel ou culturel, on se limitera à lire le commentaire de ces premières lignes.
Les trois premières lignes : les outils usuels
Elles ne changent pas d’aspect et propose les mêmes outils, mais hyperboliques, ou plus exactement les mêmes outils de géométrie dans le contexte du modèle hyperbolique du disque de Poincaré. On notera que la translation est grisée car ce n’est pas une transformation hyperbolique (l’image d’une droite n’est pas une droite). Bien entendu, l’icône de parallélisme est grisé aussi pour des raisons que l’on imagine. Les autres outils de la deuxième ligne sont valident et fonctionnent comme on s’y attend. La ligne suivante est plus parsemée, il n’y a ni le segment de longueur fixe, ni le vecteur, ni le polygone. Par contre l’angle et l’angle de mesure fixe sont disponibles dans le modèle de Poincaré.
Une mention particulière sur le point qui est nécessairement hyperbolique donc à l’intérieur du disque de Poincaré. De même on n’est pas obligé d’utiliser l’outil intersection pour prendre l’intersection de deux objets, on peut simplement créer une intersection avec l’outil point, par engagement direct, comme dans le cas euclidien.
Remarque de seconde lecture : Prendre un point idéal
Dans une utilisation classique, on n’aura généralement pas à prendre un point sur le cercle horizon, c’est-à-dire un point à l’infini. Mais dans certaines constructions cela peut être nécessaire. Or, contrairement aux apparences, le cercle horizon est caché. Pour l’utiliser, il suffit de le rendre disponible avec la baguette magique. L’utilisation seule de la baguette magique permet, dans CaRMetal, de poursuivre les constructions avec des objets cachés.
En voici une illustration avec suivi de l’historique :
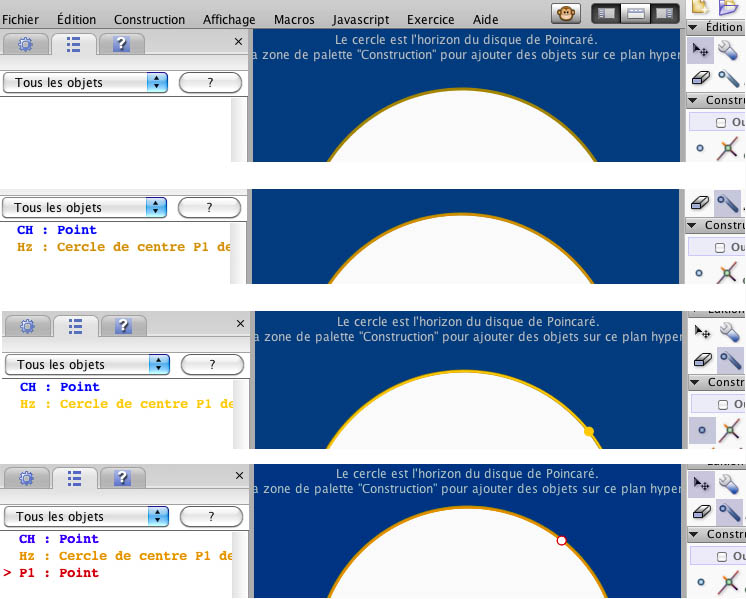
Illustration 1 : l’environnement usuel à l’ouverture d’une figure hyperbolique. Aucune construction n’apparaît.
Illustration 2 : la baguette magique rend disponible le cercle horizon Hz et son centre CH.
Illustration 3 : on pose un point sur l’horizon (avant de cliquer)
Illustration 4 : après le clic sur le point.
En décochant ensuite la baguette magique, l’horizon et son centre sont à nouveau cachés. Ils n’ont jamais été rendu visibles pour pouvoir être utilisés, seulement disponibles.
La ligne des cercles : une première spécificité
L’auteur du logiciel a choisi de conserver cette quatrième ligne de la palette de construction encore identique à la palette usuelle même si elle aussi est clairsemée. On y retrouve :
• le cercle par centre et point. Dans le modèle du disque de Poincaré, il est représenté par un cercle euclidien, mais son centre n’est pas le centre euclidien bien entendu.
• le compas. Le cercle comme outil de report de longueur d’un segment.
• le cercle circonscrit. Comme pour le cercle par centre et point, l’intitulé euclidien a été conservé mais l’outil a une spécificité hyperbolique. En effet trois points ne sont pas toujours cocycliques, mais l’outil trace bien le cycle passant par ces trois points. Voyons cela plus en détail.
La notion de cercle s’étend naturellement en géométrie hyperbolique, on parle alors de cycle. Par cycle, de pinceau donné passant par un point donné, on entend l’image du point par l’ensemble des droites du pinceau. Par exemple, si le pinceau est à centre, ce centre défini le pinceau, on parle de cercle de centré donné passant par un point donné.
Comme il y a trois types de pinceaux, il y a trois types de cycles. La première icône (cercle par centre et point) fonctionne aussi si on se donne comme centre le point idéal d’un pinceau sans support (ie à point idéal). Le cycle porte le nom d’horicycle (horocycle en anglais parfois repris en français). Dans le modèle du disque de Poincaré, c’est un cercle tangent à l’horizon en le point idéal du pinceau, ie en le centre de l’horicycle. (D’autres définitions de l’horicycle peuvent être données).
La cinquième ligne : outils spécifiquement hyperboliques
La ligne suivante contient des outils spécifiquement hyperboliques.

Deux droites non sécantes (et non parallèles) ont une et une seule perpendiculaire commune. On est dans un contexte très différent du cas euclidien (car il n’y a pas de translations usuelles). Il en résulte qu’il n’existe pas de rectangle.
L’icône intitulée « droite avec points idéaux » est plus que cela, en fait il s’agit d’une droite orientée. Si I et J sont les point idéaux de la droite (AB) avec I et J respectivement du côté de A et du côté de B alors cette configuration I, A, B, J sera toujours dans cet ordre. Compte tenu de l’implémentation des arcs de cercle en géométrie hyperbolique, un travail spécifique est nécessaire pour obtenir ce résultat (c’est un problème de continuité - continious naming problem - propre au cas hyperbolique).
Cette conservation de l’ordre est essentielle dans certaines configurations, en particulier autour des bissectrices de droites non sécantes. Elle présente de nombreux avantages, mais aussi quelques inconvénients (les configurations sont nécessairement orientées, ce qui permet de conserver une certaine continuité mais peut aussi compliquer les figures, on en reparlera dans le second article à propos de constructions propres aux trilatères) c’est pour cela que cette icône ne correspond pas à la droite usuelle.

L’icône suivante construit les deux horicycles passant par deux points A et B donnés. Comme dans le cas de la droite orientée, les points idéaux solutions sont orientés, c’est-à-dire que la continuité (de l’orientation avec les deux points) est préservée dans le déplacement des points A et B.
La dernière icône est celle de l’équidistante à une droite donnée d passant par un point donné A. On l’a déjà dit c’est l’ensemble des image de A par les symétries par rapport à toutes les droites orthogonales à d (ie du pinceau d’axe d).
Dans le cas euclidien, l’équidistante est non seulement une droite, mais c’est la parallèle à d passant par A. Dans le cas hyperbolique, ce n’est pas une droite. Sa représentation dans le disque de Poincaré est un arc de cercle.
Le fait que l’équidistante hyperbolique ne soit pas une droite a été l’une des erreurs récurrentes dans la construction de preuve du V° postulat d’Euclide : la représentation usuelle de chacun était que l’équidistante est (implicitement) une droite - puisque ce c’était le cas dans le seul modèle de géométrie que l’on connaissait.
Ortho et parallélisme
Premières activités hyperboliques sur les droites
Le polycopié de l’ensemble des activités - et la présentation des choix effectués - est téléchargeable en fin d’article, mais les copies d’écran sont dans l’article en ligne pour une lecture continue.
Dans ces onglets, nous proposons des illustrations des activités et des exemples de production des étudiants qui sont tous de futurs enseignants.
De par leur cursus, les étudiants sont largement formés à la conceptualisation et la pratique de la géométrie hyperbolique, même dans un modèle, va rapidement produire de très bonnes conceptualisations. Aussi avons nous cherché à collecter rapidement des informations sur des représentations qui vont être nécessairement furtives.
L’objectif est de montrer aux futurs enseignants que chacun de nous se construit des représentations sur ce qu’il a à travailler, voir des théorèmes en actes, et que l’apprentissage consiste à faire évoluer ces représentations. Pour voir cela, les étudiants travaillent
a) sur des domaines non connus pour voir leurs propres représentations, et
b) en géométrie dynamique car cela permet de faire évoluer leurs représentations très rapidement.
Elles vont évoluer rapidement aussi à cause de leur capacités de conceptualisation, acquise pendant leurs parcours universitaires, alors que cette capacité n’a pas la même disponibilité dans un contexte scolaire.
La première activité - Orthogonalité et rectangle
Elle est construite pour manipuler les premiers outils. Il va de soi que les étudiants ont déjà une pratique de la géométrie dynamique en général et ont fait déjà une séance sur ce logiciel, spécifiquement. Dans une présentation préliminaire, il a été dit que le modèle était conforme et cela a été illustré.

dont voici deux configurations

Nous sommes dans un contexte de type scolaire - collège - où l’on ne sait rien de la dimension théorique sous-jacente et où on nous donne des outils : règle et équerre pour observer l’orthogonalité. On notera que dans un cadre physique l’équerre sert à construire des droites orthogonale mais elle est aussi un outil de vérification instrumentale qu’un angle est droit, ce que l’on n’a pas ici : on provoque alors, de fait, une démarche a priori partiellement perceptive, même si beaucoup d’étudiants conceptualisent systématiquement leurs observations. Cela donne par exemple :
Dans l’illustration suivante, l’étudiant commence par une analyse de la situation, puis termine par une remarque qui exprimer la prégnance du modèle (« la droite devient un point »).
Cette première activité (non existence du rectangle) questionne l’habitude euclidienne. Mais contrairement à des élèves de collèges qui, souvent, attendent qu’on institutionnalise leurs observations, les étudiants cherchent à structurer conceptuellement leurs conjectures sur les nouvelles propriétés de l’orthogonalité.
Deuxième activité - Perpendiculaire commune - Parallélisme

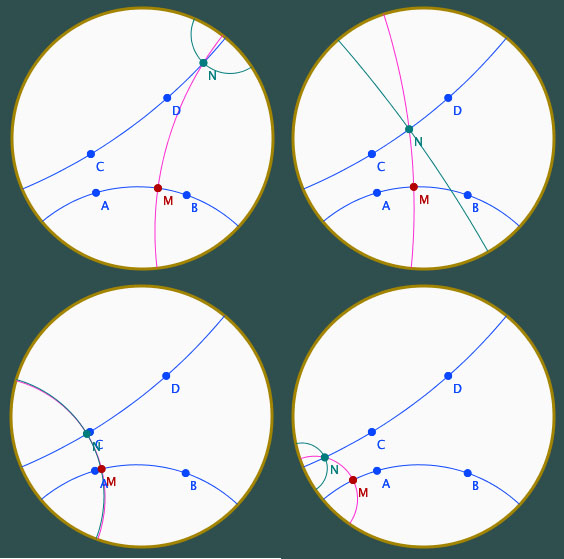
Voici deux compte-rendus différents de l’activité :


Dans le premier, l’étudiant a senti le besoin d’illustrer ses propos. Nous n’avons pas pris le temps de l’interroger sur le vif, il aurait été intéressant de savoir si l’intention était de type extrinsèque - rendre compte, vis à vis de l’enseignant, que l’on avait bien atteint l’objectif ou intrinsèque, si le texte produit, annonçant un résultat si surprenant pour l’étudiant, ne suffisait en lui-même et qu’il devait s’accompagner d’une illustration.
Dans le second extrait, le rapport à l’activité est plus formel, des conséquences logiques sont tirées.
Dans le cadre d’une analyse des productions, le premier cas rend compte sinon d’une fragilité, au moins d’un trouble vis à vis de la situation. On peut faire remarquer que nous fonctionnons tous de la même façon, et qu’il en est de même des élèves. On notera toutefois que souvent les élèves dessinent parce qu’il ne savent pas exprimer mathématiquement leur expérimentation alors que là, l’étudiant a dessiné tout en ayant parfaitement saisi et exprimé les enjeux de l’activité.
2.b. De la conjecture à l’institutionnalisation en acte
On poursuit par une institutionnalisation de la conjecture, au sens où l’on donne un nouvel outil de construction de l’objet mis en évidence dans l’activité que l’on dit « de découverte » :


L’institutionnalisation est « en acte », il n’y a pas, dans cette séance, de retour vers la théorie. Comme en classe de collège, on donne les définitions à partir de l’exploration sur un modèle. A la différence de la situation euclidienne, les étudiants voient bien que l’on est dans un modèle puisqu’ils ont, eux, le recul théorique, ce qui n’est pas le cas des élèves de collège.
2.c Vers le parallélisme
Nous abordons maintenant la phase la plus délicate de cette première partie de la séance sur la géométrie hyperbolique, la rencontre avec le parallélisme. Cette rencontre est délicate. Historiquement elle a été longtemps simplement impossible. On sait que c’est sur cette propriété que Sachcheri a bloqué (1733) alors qu’il avait été très loin dans l’élaboration des propriétés hyperboliques avant de conclure que ce que l’on va observer est « contraire à la nature de la droite », et donc qu’« Euclide est lavé de toute tache ».

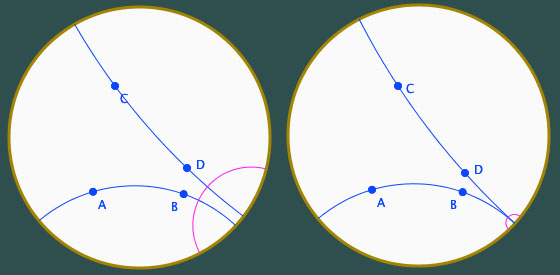
Les comptes rendus des étudiants sont écrits un peu vite, et le vocabulaire utilisé peut parfois ne pas être finement réfléchi. C’est d’autant plus intéressant que cette production reflète alors leurs représentations initiales de la situation, ce qui est assez rare à saisir chez des personnes formées à réfléchir sur des concepts très abstraits et à les manipuler dans des démonstrations. Ainsi, un retour sur leurs écritures permet d’illustrer que chacun à des représentations initiales et que si eux, de par leur formation, savent les faire évoluer très vite, sans ou avec très peu d’apport d’informations extérieures, en classe, le rôle de l’enseignant est bien de repérer les différentes représentations erronées et de construire des parcours d’évolution de ces représentation avec les élèves, et certainement pas contre eux.
Avant d’aborder les productions autour du parallélisme, voici un exemple typique de confusion entre la construction d’un objet et une approche de type « variationnelle » pour rendre compte de l’existence de cet objet :

D’une manière générale, dans certaines situations constructives, les élèves n’arrivent pas à s’extraire du geste - généralement physique, parfois mental - qui a conduit à la mise en évidence d’une situation particulière pour replacer celle-ci dans le champ des configurations. Si on rencontrer cette situation à ce niveau ce compétence, cela illustre probablement un certain désarroi non pas devant le résultat, mais plutôt devant le procédé utilisé pour l’exploration de cette géométrie si nouvelle. On retrouve le même genre d’errements en collège devant des figures de Thalès où la situation dynamique permet de valider que ce que l’on cherche existe sans que cela soit un procédé constructif de par son utilisation du mouvement.
Bilan de cette première phase
L’activité se termine par une définition de deux droites parallèles : ce sont des droites qui ne sont pas sécantes et qui n’ont pas de perpendiculaire commune. La question de l’existence de ces droites n’est pas posée, elle est vue dans le modèle.
En définitive, la version euclidienne des droites ayant une perpendiculaire commune est un cas particulier. L’aspect affine - avec son plongement projectif - est une approche plus générale : les droites parallèles sont des droites qui (projectivement) se coupent à l’infini.
Il faut toutefois être prudent avec cette représentation, car la représentation affine (et ses structures vectorielles sous sous-jacentes) ne s’étend au cas hyperbolique qu’avec précaution, par exemple cette approche ne suffit pas à assurer la transitivité du parallélisme comme on le voit ici :
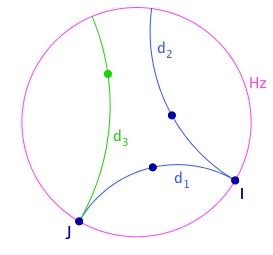
On parlera donc de droites ayant un point commun idéal. On voit bien que l’on est alors dans une géométrie du modèle. D’un point de vue théorique, on parle de bouts communs, et il y a un travail pour préciser ce concept et surtout montrer que la notion de bouts est transitive.
Deux directions pour faire un bilan de cette première phase
a) mathématique, sur le parallélisme
Même en faisant différentes variantes de cette activité, sauf à dire ce que vont être deux droites parallèles - ou par exemple qu’on veut arriver au résultat que par un point il ne passe que eux parallèles à une droite donnée, il est difficile de dégager de ce modèle (comme de tous les autres) le concept de parallélisme au sens de droites ayant un point commun à l’infini. Plusieurs raisons à cela :
- La perception du cas limite comme hors du champ de la mise en oeuvre de la modélisation. Typiquement les étudiants dans ce schéma disent « comment penser que ce n’est pas un bug du logiciel que rien se passe dans ce cas », d’où les réponses sur la perpendiculaire commune apparaissant quand les droites se coupent sur le cercle.
- La cohérence d’un point de vue différent qui, en définitive, est aussi enseigné, celle des hyperparallèles pour parler de droites ayant une perpendiculaire commune.
- Si on fait remarquer que dans ce cas il n’y a pas de transitivité du parallélisme, et donc pas de directions parallèles, ceci n’est pas considéré comme un véritable argument par ceux qui ont fait de la géométrie affine, en ce sens que l’unicité de la parallèle, dans le cas euclidien est équivalent à la transitivité du parallélisme.
- Le cas « exceptionnel » du parallélisme au sens de Lobatchevski, vu comme marginal et non significatif (alors que le cas affine est tout autant « marginal » et « significatif ») qui dans le contexte du point précédent prend le nom de « parallèles limites ».
b) didactique sur l’enseignement qu’apporte l’analyse de l’information recueillie
Dans le cadre d’une formation initiale (typiquement des M1) il est important de bien fixer le cadre en amont, par exemple sur la base d’un travail antérieur d’analyse de travaux d’élèves : nous allons entreprendre un travail de recueil de production avec eux, pour les replacer, dans un contexte de géométrie élémentaire, dans la situation d’enseignement du collège, avec une axiomatique peu claire qui mélange les objets mathématiques et leurs représentations physique à travers le modèle standard.
Pour certains étudiants, cette homologie didactique « forte » peut être mal perçue. Les réactions négatives peuvent être de plusieurs types, portant :
• sur une rupture, ou une ambiguïté du contrat : « Vous nous laissez écrire des choses fausses ».
• sur une rupture du type d’enseignement/formation.
• sur une perte de repère, soit géométrique, soit culturel dans l’approche non conceptuelle de cette géométrie : « On aurait préféré un vrai cours sur la géométrie hyperbolique », c’est-à-dire une réaction de vrai étudiant - qu’ils sont encore - pas vraiment sensibilisé aux problématiques que l’on voulait soulever dans cette activité.
Dans une formation, c’est l’occasion, de faire vivre, avec l’analyse des productions, les gestes professionnels que l’on attendra plus tard des futurs enseignants. Plusieurs pistes sont possible :
• La mise en avant les représentations premières qui, chez eux sont vite balayées (d’où la prise de note de ces premières représentations) alors qu’elles sont persistantes chez les élèves de collège. Statistiquement, il y a toujours quelques étudiants qui, donnant des cours, peuvent témoigner de cette persistance, de l’intérêt de ces analyses de production en terme de représentation.
• Dégager, et reconnaitre la logique souvent développée d’une cohérence interne à un raisonnement qui ne correspond pas à la situation hyperbolique comme décrit au deuxième point du a).
• En lien avec le point précédent, dire quelques mots sur la longue réflexions des mathématiciens sur la géométrie, et les différentes erreurs - dont celle de Sachcheri - faites par les meilleures
• Remarquer que même sur un modèle, il faut du temps pour interpréter ce que l’on voit, et encore plus pour être capable de le conceptualiser de manière satisfaisante. C’est toute la dialectique opérationnalité/conceptualisation qui se retrouve, dans l’enseignement dans la dialectique outil/objet : on sait qu’il faut souvent plusieurs années entre le moment où un outil maitrisé de manière technique puise devenir un objet de savoir utilisable dans des démarches hypothético-déductives.
La suite de la séance sera plus centré sur des résultats mathématiques, et ne pose pas autant de difficulté que cette première introduction.
Droites du triangle
Les hauteurs d’un triangle

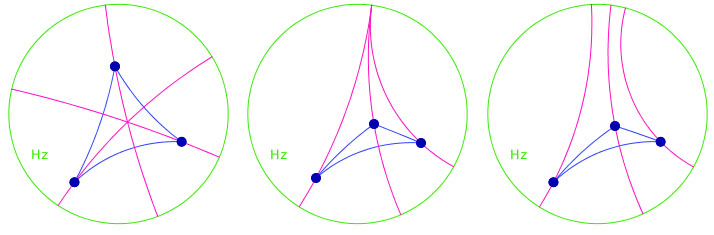
L’activité sur les hauteurs est naturelle dans continuité de l’activité précédente, c’est l’occasion pour chacun de faire fonctionner le vocabulaire qui a été précisé en conclusion de l’activité précédente. Les commentaires vont donc être imprégnés des résultats précédents.
Institutionnalisation des observations
L’activité sur les hauteurs étant rapidement faite, les étudiants perçoivent bien un nouveau mode de fonctionnement : les droites remarquables ne vont pas être seulement concourantes mais vont avoir des choses en commun. Tout comme en cours de géométrie au collège, on peut alors donner des définitions opérationnelles pour faire des démonstrations sans pour autant que ces définitions soient mathématiquement clairement précises : c’est la différence entre le savoir enseigné et le savoir savant.
a) le savoir enseigné
On remarque que ces hauteurs ont soit un point en commun, soit une perpendiculaire commune en commun, soit encore - même si c’est difficile à réaliser, un point à l’infini (elles sont toutes les trois parallèles).
On dira que les droites sont en pinceau si elles ont une de ces trois propriétés en commun.
Il y a donc trois types de pinceaux dans le cas hyperboliques :
• à centre : les droites ont un point en commun,
• à axe : les droites ont une perpendiculaire en commun,
• sans support : les droites ont un point idéal commun, elles sont parallèles.
On admettra, comme théorème général, que les droites remarquables d’un triangle (hauteurs, médiatrices, médianes, bissectrices) sont en pinceau. Par ailleurs un résultat non trivial est que les médianes d’un triangle sont toujours en pinceau à centre.
Cette définition opérationnelle donnée, comme en classe avant une démarche hypothético-déductive, il y a beaucoup d’implicite sur le concept de pinceau de droites.
En particulier, contrairement aux apparences, un implicite, de fait, perceptif, qu’il est facile de faire passer pour conceptuel même en M1 de mathématique, est que les trois types de pinceaux sont disjoints. Cela se voit sur le modèle : si deux droites sont séca,ntes elles ne peuvent avoir une perpendiculaires commune ! Or ce sera vrai dans le cas elliptique. Et comme toute géométrie - même l’hyperbolique - se plonge dans une géométrie projective (où tous les pinceaux sont à centre), on voit bien que cette disjonction n’est pas évidente en soi, et qu’il y a, de fait, une utilisation manifeste des représentations sur le modèle hyperbolique étudié pour mettre en oeuvre cette disjonction des types de pinceau (vraie) et pouvoir l’utiliser dans les preuves des prochains onglets.
En fait l’ambiguïté vient de ce que nous sommes dans un modèle et donc ce qui est vrai dans la géométrie est vrai dans le modèle, mais ce qui est vrai dans le modèle (en particulier à sa frontière) n’est pas nécessairement vrai dans la géométrie - même si, bien interprété, c’est toujours le cas pour la géométrie hyperbolique.
b) le savoir savant associé
La théorie générale sous-jacente utilisée ici est l’axiomatique de Bachmann, une axiomatique construite sur la base des premiers théorèmes sur les pinceaux de Hjelmselv (1907), pour proposer une construction purement algébrique, construite sur les isométries. C’est en particulier une géométrie où il n’y a pas de notion d’ordre a priori, pour que l’axiomatique contienne aussi le cas elliptique. Ce travail s’est partiellement construit en réaction aux Fondements de la Géométrie de Hilbert, ouvrage auquel Bachmann a activement participé, à partir de la septième édition, travaillant sur la notion d’ordre en particulier.
Sans entrer en détail dans cette axiomatique (elle sera décrite dans le second article, elle est déjà présentée en détail dans cet ancien travail de l’auteur - 139 pages largement illustrées 9,4 Mo) donnons quelques précisions sur le savoir savant associé au « savoir enseigné » ci dessus.
En fait, il y a deux notions bien distinctes : tout d’abord, celle de droites en pinceau, et ensuite celle de pinceaux de droites. Dans la définition opérationnelle, intuitive, ces deux notions ne sont pas clairement dissociées car même si elles sont implicitement présentes, elles s’appuient sur un mélange de définitions et d’approches perceptives dans le modèle hyperbolique.
Chacun peut vérifier rapidement que les médiatrices d’un triangle sont en pinceau, les médianes aussi. On vérifia que la droite d’Euler hyperbolique n’existe pas : quand ils existent, O, G, H ne sont pas alignés. Le fait que les points ne soient pas alignés dans un modèle suffit à prouver qu’ils ne sont pas alignés en géométrie hyperbolique.
Nous verrons que plusieurs autres propriétés euclidiennes sont en fait absolues, alors qu’on les démontre généralement soit par les barycentres, soit avec la cocyclicité, deux propriétés euclidiennes.
Un premier théorème
Le théorème absolu des milieux
Nous allons démontrer un premier théorème hyperbolique, et même plus généralement absolu (ie aussi elliptique, mais c’est une autre histoire), le « théorème des milieux » qui correspond à l’un des premiers théorèmes montrés en classe de 4°. Pour cela on suppose acquises quelques propriétés sur les symétries orthogonales et les symétries centrales, des propriétés en fait purement algébriques, dues à l’ordre des éléments, à savoir qu’une symétrie centrale de centre I est la composée de deux symétries orthogonales d’axes sécants en I, cette composée étant alors commutative.
L’activité proposée

La figure associée

Le raisonnement mathématique
C’est-à-dire un triangle ABC, la droites ∆=(IJ), droite des milieux de deux côtés du triangle, les droites $d_1$ et $d_2$ perpendiculaires à ∆ en I et J.
Alors on a classiquement $s_J$ o $s_I$ = ($s_{d2}$ o $s_\Delta$) o ($s_\Delta$ o $s_{d1}$) = $s_{d2}$ o $s_{d1}$.
En particulier C = $s_J$ o $s_I$(B) = $s_{d2}$ o $s_{d1}$(B)
Nommons M = $s_{d1}$(B), alors C = $s_{d2}$(M), ce résultat n’étant qu’un résultat algébrique, que nous allons maintenant interpréter géométriquement.
Dans le triangle BMC, d’après ce qui précède, $d_1$ est la médiatrice de B et M (définition de M) et $d_2$ celle de M et C (par propriétés algébriques). Or ces deux droites ont une propriété bien particulière, elles ont une perpendiculaire commune, la droite (IJ).
Comme le triangle BCM a deux de ses médiatrices en pinceau à axe (ce vocabulaire mélange les deux notions de pinceaux pour ceux qui ont réroulé le bloc ci-dessus), mais dans une version plus proche du "savoir enseigné", on dira que deux médiatrices ayant une perpendiculaire commune, le pinceau des médiatrices est nécessairement "à axe". Cet axe étant la droite des milieux (IJ).
Que venons-nous de démontrer ?
Plus précisément quelle peut être une version absolue (ou déjà hyperbolique) du théorème du milieu ?
Cette question laisse régulièrement les étudiants dans une certaine perplexité. Certains font ce que Duval appelle « un pas de démonstration de plus », comme en classe de collège, en annonçant :

ou encore

Quelques étudiants cherchent à décontextualiser l’expression du même résultat

En insistant sur la recherche d’un théorème des milieux que le résultat précédent exprime, les productions font apparaître la perpendiculaire commun, mais dans une formulation qui n’est pas pertinente, comme :

Les difficultés d’expression
Cet exemple du théorème des milieux est proposé pour placer les étudiants dans une situation de difficulté d’expression comme peuvent la vivre les élèves de collège pour qui les concepts proposés à la manipulation, et les relations entre ces concepts ne sont pas encore totalement clairs. Il s’agit aussi de faire prendre conscience de la difficulté à voir ce qui est nouveau et pertinent dans une situation, même élémentaire comme ici. En pratique, dans un premier jet, les étudiants rédigent des propriétés généralement vraies, encore assez éloignées du théorème des milieux.
Les exemples précédents sont significatives des productions en général, et elles illustrent deux choses :
• la difficulté de dépersonnalisation, et, malgré des tentatives intéressantes,
• la difficulté de réellement décontextualiser la situation.
Le Théorème absolu des milieux
Plusieurs expressions peuvent être proposées, et celle-ci, obtenue dans une seconde écriture, en insistant sur la recherche d’une expression qui soit correcte aussi bien en géométrie euclidienne qu’hyperbolique est une belle exception parmi les productions effectuées en séance par les étudiants :

En effet l’article indéfini une, en tant que tel, ne renvoie ni à l’unicité ni à la non unicité, la formulation est donc bien absolue.
Néanmoins, pour une expression encore plus neutre de la propriété absolue, on peut aussi s’arranger à ne pas avoir à formuler d’article comme dans cette formulation :
Dans un triangle, la droite des milieux de deux côtés et le troisième côté du triangle admettent comme perpendiculaire commune la médiatrice du troisième côté.
Commentaires sur l’activité
Contrairement à la situation des droites parallèles pour laquelle les étudiants perçoivent l’aspect intrinsèque de la difficulté générale, et donc ne se sentent pas du tout en cause dans un échec de perception de la notion, dans cette activité de démonstration, la non perception du théorème des milieux peut être parfois très mal vécue par certains étudiants.
L’évidence d’une expression comme l’encadré ci-dessus, mis en relation avec l’incapacité à « voir le théorème » qui vient d’être montré, dans un contexte de géométrie élémentaire de classe de quatrième, est une expérience d’homologie didactique forte, qui peut être difficile à vivre pour certains, mais cela reste une vraie expérience de didactique ... appliquée à soi-même.
Cercles
Le cercle comme cycle à centre
La fiche de travail se poursuit par les cercles et cycles. Selon le type de séance (3 h ou 4 h) et l’aisance préliminaire avec le logiciel, le première activité sur les cercles est commencée en présentiel ou non. Le travail de preuve, dans la deuxième partie de cette activité, est à rédiger en dehors de la séance. La suite aussi.
On commence par une approche « absolue » du cercle, basée sur les symétries. Cette approche permet d’avoir une définition qui va pouvoir s’étendre à d’autres objets dont le cercle est un cas particulier. Toutefois, la vérification de la conjecture est plus technique.
L’activité proposée sur le cercle hyperbolique

Cette activité est construite en deux parties, une première d’exploration et une seconde de réflexion, et de mise en œuvre des outils dégagés dans les activités précédentes.
L’exploration sur le cercle
Pour explorer la représentation du cercle hyperbolique dans le modèle euclidien du disque de Poincaré, on fait le lieu de l’image A’ de A par les droites passant par O. Faisant cela on construit un droite (OI). Faisant le lieu quand I décrit la cercle horizon, de fait A’ fait deux tours et donc le lieu est sur deux tours, même si perceptivement, cela ne se remarque pas :
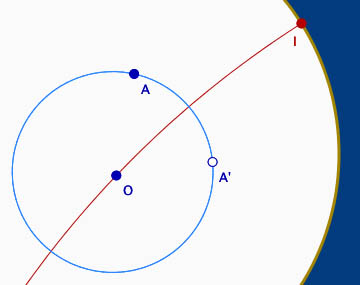
Ainsi, en prenant trois points sur le lieu (question 6.b), on construit le cercle euclidien passant par ces trois points. L’outil construit le centre. On voit alors, par la mesure de longueur des rayons, que A et A’ ne sont pas sur le cercle construit.

Cette manipulation semble donc infirmer que la représentation du cercle hyperbolique dans le modèle utilisé soir un cercle euclidien. En fait, naturellement, les points sur lieu ne sont pas des point sur l’objet qu’il représente : perceptivement le cercle circonscrit recouvre le lieu, mais on n’a pas la précision d’un calcul à cinq décimales des longueurs : on fait un calcul très précis sur des constructions approximatives, à cause des points pris sur un lieu.
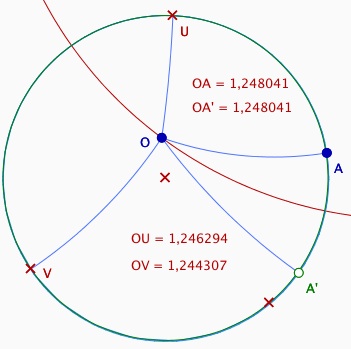
Même si ce n’était pas demandé dans l’activité, voici une confirmation directe du fait que les points pris sur le lieu ne sont pas exactement des points du cercle hyperbolique : dans l’illustration ci-dessous, on mesure la distance au centre hyperbolique, on voit bien que si OA=OA’, cette longueur n’est pas celle de OU ni celle de OV.
Pour tester effectivement la conjecture, il faut utiliser des points effectivement sur le cercle hyperbolique. C’est la question 6.c. Elle consiste à faire ceci :
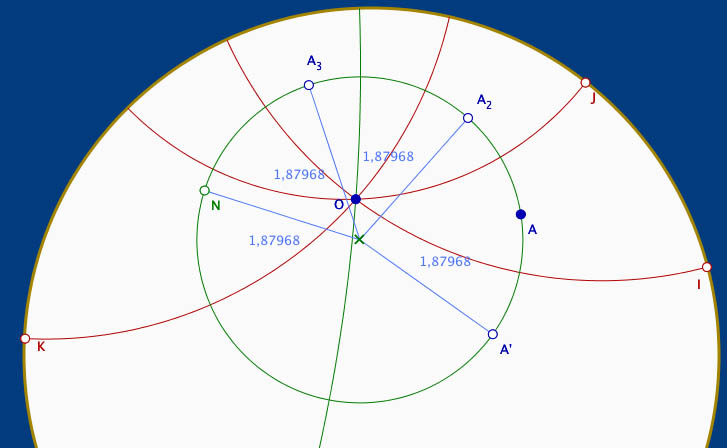
Cette fois les trois points sont, par définition des points du cercle hyperbolique de centre O passant par A, on en construit un quatrième, le point N. On vérifie ensuite, en passant sur la palette euclidienne, ...

... par l’outil distance euclidienne, que ce point N (quand un point M non visible ci-dessus parcourt le cercle horizon) est bien sur le cercle euclidien circonscrit aux trois points de base du cercle hyperbolique : cette activité renforce donc la conjecture que la représentation du cercle hyperbolique est un cercle euclidien dans le modèle utilisé.
Premières propriétés du cercle
Un fois ce résultat institutionnalisé, la fiche de travail propose ensuite une réflexion autour du cercle et de ses propriétés. il s’agit maintenant de démonstrations hyperboliques sur le cercle hyperbolique.
Question 6.d. Que dire des médiatrices de trois points pris sur un cercle hyperbolique ?
La question est proposée pour montrer les subtilités des implicites dans nos raisonnements : les étudiants voient les implicites dans les raisonnements des élèves mais pas dans leurs propres preuves. Sur plusieurs années où cette question a été posée, en pratique un implicite a toujours été mis en œuvre, à savoir que si un point B appartient au cercle de centre O passant par A, alors ce cercle est aussi celui de centre O passant par B.
Cet implicite prend des formes d’expression subtilement différentes comme ici :

On imagine bien que ce résultat est vérifié, mais de fait, même chez des étudiants de M1, on rencontre systématiquement ce que Gérard Vergnaud appelle un « théorème en acte », un résultat évident pour chacun, et de fait utilisé comme implicite par les étudiants.
Cette propriété est une conséquence des résultats sur les médiatrices :
• Si B est un point du cercle C(O, A), alors C(O, B) = C(O, A).
Preuve : soit M un point de C(O, A), le cercle de centre O passant par A. Montrons que ce point M est un point de C(O, B). Les points B et M étant sur le cercle de centre O passant par A, les médiatrices de [OA] et de [OB], axes de symétrie de O et O, et O et B respectivement, passent par O. Alors le triangle OAB a deux médiatrices sécantes en O, la troisième médiatrice, celle de B et M, passe aussi par O et donc la symétrie qui envoie B sur M passe par O et donc M appartient au cercle de centre O passant par B. On a ainsi une première inclusion, l’autre est obtenue en inversant les rôles de A et B.
• Il résulte de ce premier résultat que si deux points P et Q sont sur le cercle de centre O passant par M, alors la médiatrice de P et Q passe par O. Et donc il en résulte alors que les médiatrices de trois points d’un cercle hyperboliques sont concourantes en O.
En pratique les rédactions proposées pour cette question considèrent de fait qu’étant donné trois points A, B, C d’un cercle hyperbolique de centre O, ce cercle est le cercle de centre O passant par A. La preuve proposée est alors une variante du résultat implicite ci-dessus.
• Réciproquement si les médiatrices d’un triangle ABC sont concourantes en un point O, le même raisonnement montre que B et C appartiennent au cercle C(O, A).
Question 6.e. Trois points d’un cercle ne sont pas alignés. Conséquence : propriété de la tangente.
L’argument attendu est celui-ci (extrait d’une copie de M1 2010) :
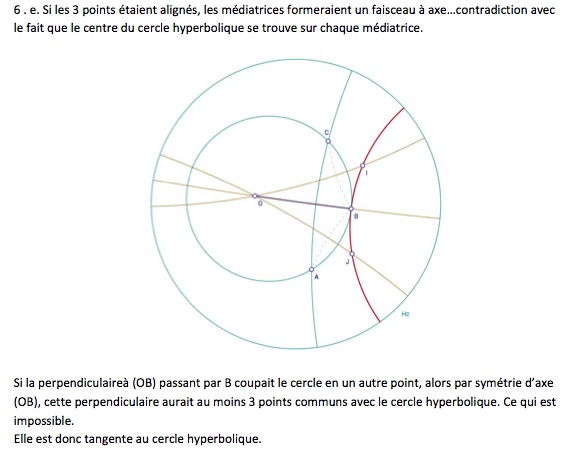
Cette question utilise le fait qu’un pinceau de droites « à centre » n’est pas « à axe ». Mais si dans une géométrie un pinceau « à centre » était aussi « à axe », alors les droites seraient aussi des cercles particuliers. C’est par exemple le cas en géométrie elliptique, mais ce n’est pas d’actualité dans cette fiche.
Par contre, toujours dans cette promotion M1 2010, on trouve aussi des arguments qui ne font que refléter la mise en œuvre des représentations que l’on a des objets que l’on manipule, comme par exemple :

L’activité sur les cercles se termine sur la remarque que la propriété du triangle rectangle en A pour un triangle ABC inscrit dans un cercle de diamètre [BC] n’est pas hyperbolique. C’est l’occasion de dire à nouveau qu’une propriété fausse dans un modèle est une propriété fausse pour la géométrie.
Compte tenu de la définition du cercle comme image d’un point par un pinceau à centre, il est clair qu’il existe, a priori, deux autres types de cycles, pour chacun des deux autres types de pinceaux.
C’est ce qui va être exploré dans le prochain onglet.
Autres cycles
L’équidistante comme cycle à axe
L’activité va se dérouler comme celle du cercle, en étant toutefois plus simple dans ses conjectures et leurs validations. Elle est présentée ainsi :

Construction et exploration de la nouvelle courbe
La construction de la question 7.a aboutit à une première courbe

Comme le disent parfois les étudiants, cela correspond à « une sorte de cercle à axe ».
Par construction les points B et C, symétriques de A dans une symétrie d’axe orthogonal à la droite ∆, sont des points de la courbe. Donc pour une exploration de l’objet euclidien qui représente cette construction hyperbolique, on passe en mode euclidien. On conjecture fortement que la représentation euclidienne est un arc de cercle. En traçant les médiatrices euclidiennes de A et B puis de A et C, et en notant $O_{Euc}$ leur intersection (centre du cercle circonscrit euclidien à ABC), on peut vérifier que la longueur euclidienne OA’ est égale à la longueur euclidienne de OB.
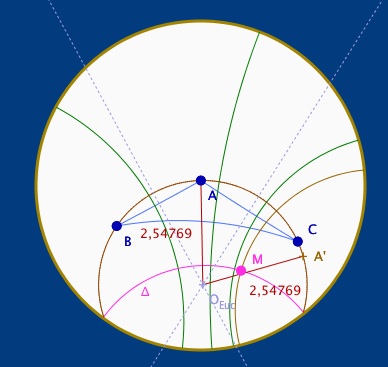
On renforce donc, numériquement, la conjecture : le « cercle à axe » se représente par un arc de cercle.
Une première construction élémentaire - c’est-à-dire non optimisée - se fait comme pour le cercle : on prend 2 autres points N et P sur l’axe, on construit les symétriques de A par rapport aux droites orthogonales à l’axe passant par N et P. On construit ensuite le cercle euclidien passant par ces trois points. On constate qu’il coupe le cercle horizon en les points idéaux de l’axe. On construit l’arc cherché.
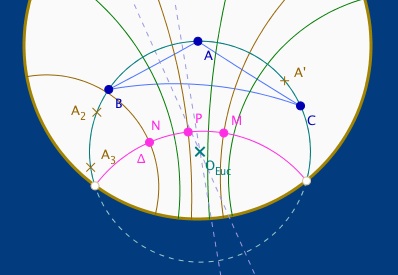
Toujours dans le mode euclidien, on peut ensuite vérifier numériquement, pour renforcer la conjecture, que B et C appartiennent bien à cet arc de cercle :

Propriétés de l’équidistante
Définition : on appelle équidistante d’axe d passant par A le lieu des images de A par le pinceau d’axe d.
Une année, une étudiante a eu cette phrase extraordinairement poétique pour décrire sa représentation du passage du cercle à l’équidistante et du pinceau à centre au pinceau à axe : « c’est un peu comme si on défaisait le nœud qui tient les droites concourante en un point et qu’on dépliait le ruban : le cercle à centre devient un cercle à axe ».
Avant de poursuivre, nous considérons comme institutionnalisé que, l’équidistante, ce « cercle à axe », est représenté par un arc de cercle dans le modèle du disque de Poincaré.
Même si ce n’est pas directement utile pour la question suivante, on peut déjà remarquer, en notant Equi(d, A), l’équidistante d’axe d passant par A, que pour tout point B de Equi(d, A), alors Equi(d, B)=Equi(d, A). L’argument est le même qu’avec le cercle car il porte sur le partitionnement des pinceaux : un pinceau à centre ne peux pas être à axe et réciproquement.
L’activité proposée se poursuit par une réflexion sur le fait que l’équidistante hyperbolique ne peux pas être une droite (7.d).
On considère une équidistante Equi(d, A) et deux points B et C de cette équidistante. Par définition de l’équidistante, les médiatrices de A et B d’une part et de A et C d’autre part ont la droite d comme perpendiculaire commune.
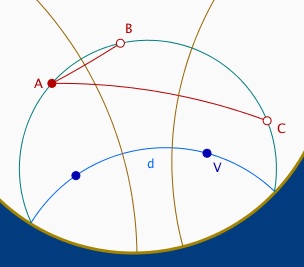
Or la première médiatrice est orthogonale à (AB) et la seconde à (AC) : si C appartenait à la droite (AB), les droites d et (AB) auraient les deux médiatrices comme perpendiculaires communes distinctes, ce qui est impossible.
Ainsi, l’équidistante, en géométrie hyperbolique, l’est pas une droite hyperbolique, c’est une nouvelle courbe hyperbolique.
L’équidistante euclidienne
Bien entendu, on peut construire l’équidistante Equi(d,A) euclidienne. Mais comme il existe des rectangle en géométrie euclidienne, l’équidistante Equi(d, A) n’est rien d’autre que la parallèle à d passant par A. Et en particulier c’est une droite.
Historiquement plusieurs démonstrations erronées du V° postulat d’Euclide (entre le IX° et le XII° s) reposent sur l’utilisation implicite que l’équidistante est une droite.
C’est en cela que le concept d’équidistante prend tout son sens dans le cas non euclidien.
Pourquoi « équidistante » ?
Parce qu’on préfère parler de transformations plutôt que de géométrie métrique, on peut justifier le terme équidistante par le fait que les symétries orthogonales sont - a priori dans notre approche - (données comme) des isométries. On a donc les égalités de longueurs (figure ci-dessous) BB’ = AA’ et CC’ = AA’.
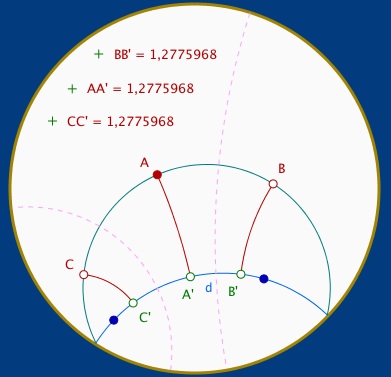
En pratique, les étudiants ont souvent « envie de vérifier », et donc, ils font comme on le ferait en classe de 5° : sans véritablement s’être posé la question de la mesure, mais en se doutant bien qu’elle existe, ils utilisent spontanément le double décimètre hyperbolique à portée de main et vérifient comme ci-dessus.
L’horicycle comme cycle sans support
Après les deux premiers cycles, on explore le dernier cas hyperbolique, un peu plus rapidement car c’est fondamentalement la même démarche, même si, là encore on obtient un objet spécifiquement hyperbolique, et qui plus est un objet important mathématiquement.
La présentation d’une activité d’investigation se présente de la même façon avec toutefois une petite difficulté technique résolue par l’utilisation d’un outil construit partiellement pour cela :

L’illustration suivante correspond à l’activité préalable, les deux points roses sont les poignées de la première droite, puis une autre poignée d’une autre droite est construite. Pour construire des droites à partir d’un point idéal, il est préférable (mais non nécessaire) de montrer le point idéal en premier. On comprend bien que, là encore, cette possibilité est une extension de la droite hyperbolique. Se donner un point idéal c’est comme se donner une direction de droite dans le cas euclidien.
Le point I, point idéal du modèle hyperbolique, s’appelle parfois un « bout » des droites (chez Bolyaï, ou chez Hilbert). C’est une façon aussi de nommer la direction des droites parallèles en restant dans le modèle. Un pinceau sans support peut alors être aussi appelé un pinceau de bout I.
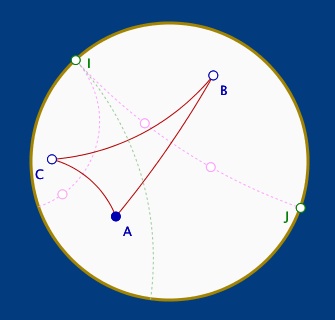
En vert pointillé, on a tracé la troisième médiatrice, celle de B et C. Dans le modèle, elle passe par I car les médiatrices sont en pinceau, et les deux premières, par construction, sont parallèles de bout I.
La construction de l’horicycle comme lieu est immédiate, et le lieu plus précis que dans le cas du cercle car quand le point M parcours le cercle horizon, on ne parcours toutes les droites du pinceau de bout I qu’une seule fois, et non pas deux comme dans le cas du cercle.

Clairement, dans ce modèle, l’horicycle est représenté par un cercle euclidien tangent à l’horizon en un point qui est le bout du pinceau. Nous ne rendrons pas compte des vérifications désormais usuelles, elles se font comme dans les deux cas précédents.
Une propriété de l’horicycle
Par contre arrêtons nous à une propriété de l’horicycle qui, dans d’autres présentations, sont sa définition.
Tout d’abord, comme pour le cercle, ou l’équidistante, trois points d’un horicycle ne peuvent être alignés, sinon les médiatrices de ces trois points seraient à axe, or elles sont en pinceau sans support (de même point idéal).
Il en résulte que pour un horicycle de point idéal I, la perpendiculaire à une droite du pinceau issue de I, en le point d’intersection M de la droite et de l’horicycle est tangente à l’horicycle (un seul point d’intersection), sinon elle couperait l’horicycle en M, en un autre point et en le symétrique de ce point par rapport à (IM).
Autre point de vue : si la perpendiculaire en M à la droite (IM) coupait l’horicycle en N, la médiatrice de M et N (en marron sur l’illustration suivante), par conservation de l’angle droit en M par la symétrie d’axe la médiatrice, (IN) serait orthogonale à (MN). Donc (MN) serait une perpendiculaire commune à (IM) et (IN) qui sont parallèles.

C’est pour cette propriété que le point idéal est généralement appelé le centre de l’horicycle : l’horicycle est alors un cercle de centre un point à l’infini passant par un point donné, ce qui, dans le cas euclidien, est encore une droite, orthogonale à la direction des parallèles issues du point à l’infini).
Dans des présentations plus orientées vers la géométrie différentielle, la propriété précédente est parfois une définition de l’horicycle de centre (idéal) I passant par A : c’est la courbe passant par A, orthogonale en chacun de ses points à la droite du pinceau passant par ce point.
Complément culturel : la validation de la géométrie hyperbolique
Les horicycles ne sont pas des droites, mais comme objets n’ayant qu’un point à l’infini, les horicycles concentriques peuvent être considérés comme parallèles. Alors Bolyaï et Lobatchevski ont montrés (en se plaçant dans le contexte plus général de l’horisphère - sphère privée d’un point) que la géométrie sur les horicycles est euclidiennes (d’où une version hyperbolique de la propriétés de Thalès sur les horicycles) : ainsi les deux géométries – hyperboliques et euclidiennes – sont liées, et si la géométrie euclidienne est supposée « non contradictoire », il en résulte que c’est aussi le cas de la géométrie hyperbolique. C’est en ce sens qu’a été validée la consistance de la géométrie hyperbolique, en 1832, bien avant qu’on puisse en donner les premiers modèles (partiel Beltrami -1868 puis complet Klein 1869).
Cette première présentation de la géométrie hyperbolique est restée résolument du côté des configurations, sans même indiquer comment se calcule la distance hyperbolique, elle est fournie comme serait fourni un double décimètre en classe : on en n’a jamais eu besoin, elle n’est fournie que pour « rassurer » certains étudiants ...
Cette présentation a aussi été centrée sur une réflexion de l’appropriation de la précision dans les démonstrations en géométrie. Que les lecteurs troublés par cette démarche d’homologie didactique soient rassurés : le prochain article, sur les pinceaux et des outils propres dans CaRMetal (à partir de la version 3.6.5), justifieront l’essentiel des points seulement conjecturés ici. En attendant, le lecteur curieux peut consulter ces anciennes pages - du même auteur - sur la question en CabriJava, mais non maintenues depuis.
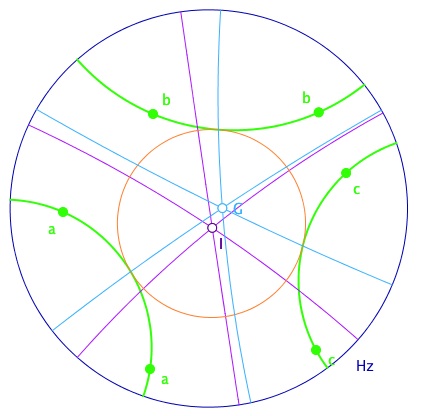
Cette première approche sur les pinceaux peut se résumer sous la forme de ces deux tableaux :

On notera dans le second tableau le mélange implicite des deux types de pinceaux : au centre on parle de droites en pinceaux, dans la colonne suivante, de pinceaux de droites.
Téléchargements associés
Le logiciel CaRMetal (libre, sous licence GNU, multiplateforme)
Les figures associées à cet article manipulables en ligne.











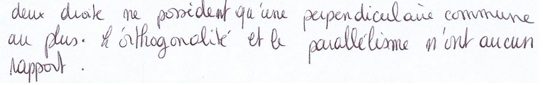




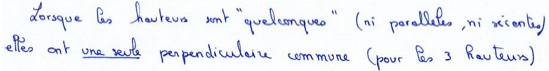


Commentaires