Dans cet article, nous allons parcourir les différentes questions notamment celles demandant de la programmation. Nous donnerons la version POO, la version Python fonctionnel et la version OCaml proposée par Charignon.

Commençons par montrer quelques exemples d’appels avec la POO :

Exemples de manipulations

Création d’un tablier européen et affichage

6        50 51 52      
5     41 42 43 44 45
4  32 33 34 35 36 37 38
3  24 25 26 27 28 29 30
2  16 17 18 19 20 21 22
1      9 10 11 12 13
0         2  3  4
    0  1  2  3  4  5  6

Création d’un motif vierge sur tablier européen

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Remplir l’encoche aux coordonnées 3, 3

>>> M0.switch(3, 3)
>>> print(M0)

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ●  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Demander à l’encoche 3, 3 son numéro

>>> M0.encoche(3, 3).num
27

L’encoche 27 est-elle remplie ?

>>> M0.encoche(27).on()
True

Demander au motif de vider son encoche 27

>>> M0.switch(27)
>>> M0.on(27)
False

Dans ce début de sujet, il est question des différentes formes de tablier ainsi que de la numérotation des encoches. Comme nous le voyons sur les exemples, une encoche est représentée par des coordonnées x, y et un numéro entier fonction des ces coordonnées.

Nous allons donc commencer par créer une classe Tablier, le support de nos Motifs. Nous pourrons créer un tablier européen ou unidimensionnel. Ce qui les différencie : la dimension et la façon de numéroter les encoches.

La classe Tablier va implanter la méthode __str__ qui permettra d’afficher les numéros des encoches.

Les contraintes nous sont données par l’énoncé du sujet. Pour le tablier européen :

Nous numérotons l’encoche de coordonnées (x, y) ∈ ℕ² dans le tablier européen par l’entier z = 8y + x ∈ ℕ. Nous notons l’ensemble des numéros d’encoches du tablier européen par :

E = 8y + x ; (x, y) ∈ ℕ² avec 0 ≤ x, y ≤ 6 et |x − 3| + |y − 3| ≤ 4 ⊆ ℕ

Ce qui nous permet de spécialiser notre tablier :

Question 2

class Europeen(Tablier):
    # ...
    def numero_interieur(self, z):
        return self.inside(*self.num_to_coords(z))

def foo(a, b, c):
    return a**3 + b**3 + c**3

t = 1, 2, 3
foo(*t) == 36

def numero_interieur(z):
    y, x = divmod(z, 8)
    return 0 <= x <= 6 and 0 <= y <= 6 and abs(x - 3) + abs(y - 3) <= 4

let numero_interieur z =
    let x, y = z mod 8, z / 8 in
    0 <= x && x<= 6
    &&0 <= y && y<= 6
    && abs (x−3) + abs (y−3) <= 4
;;

Question 3

class Europeen(Tablier):
    # ...
    def coordonnees(self):
        return [(x, y) for x in range(self.size) for y in range(self.size) if self.inside(x, y)]

    def numeros(self):
        return sorted(self.coords_to_num(x, y) for x, y in self.coordonnees())

NUMEROS_EUROPEENS = [n for n in range(53) if numero_interieur(n)]

let rec intervalle a b =
    if a>b then [] else a::intervalle (a+1) b
;;
let numeros_europeens =
    List.filter numero_interieur (intervalle 0 53)
;;

Question 4

Nous terminons cette partie préliminaire avec une question sur les encoches voisines d’une encoche. En regardant la figure ci-dessous,

on constate que si z est le numéro d’une encoche valide sur un tablier européen alors les quatre voisines, lorsqu’elles existent, sont : z+1 (encoche à droite), z-1 (encoche à gauche), z+8 (encoche au-dessus), z-8 (encoche en-dessous).

Le script complet pour les classes de tablier :

Cette section ne répond pas aux questions du sujet directement mais présente les classes Motif et Encoche pour modéliser le problème et préparer la suite des questions.

Encoche

Une encoche est définie par :

• un tablier
• des coordonnées x, y
• un numéro
• un état (vide ou plein)

On doit pouvoir créer une encoche en spécifiant ses coordonnées ou son numéro, en précisant obligatoirement un tablier et facultativement son état.
On doit pouvoir remplir ou vider cette encoche.

Le passage des coordonnées au numéro et vice versa va se faire par deux méthodes qui vont s’appuyer sur les méthodes du tablier.

Voici une première définition de la classe Encoche :

class Encoche:

    def __init__(self, tablier, *args, etat=VIDE):
        self.tablier = tablier
        if len(args) == 2:
            self.x, self.y = args
            self.num = self.to_num(self.x, self.y)
        else:
            self.num = args[0]
            self.x, self.y = self.to_coords(self.num) 
        self.etat = etat
    
    def to_num(self, x, y):
        return self.tablier.coords_to_num(x, y)
    
    def to_coords(self, num):
        return self.tablier.num_to_coords(num)
    
    def switch(self):
        self.etat = 1 - self.etat

Pour ce qui est de l’affichage, une encoche va se présenter sous la forme d’un jeton plein (●) ou vide (○).

On se donne une constante :

JETONS = '○', '●'

Et une méthode :

class Encoche:
    # ...
    def jeton(self):
        return JETONS[self.etat]

Motif

Un motif est un ensemble d’encoches sur un certain tablier. On doit pouvoir créer un motif :

• vierge (toutes les encoches sont vides) : M0 = Motif(euro)
• copie d’un motif existant : M0bis = Motif(euro, M0)
• en spécifiant une liste d’encoches à remplir, par leurs coordonnées ou leur numéro : M1 = Motif(euro, [12, (2, 3), (6, 2), 52]

Début de notre classe Motif :

def foo(a):
    return a

Un motif possède donc un attribut encoches qui est un dictionnaire dont les clés sont des coordonnées valides pour le tablier du motif et les valeurs associées des encoches.

Lors de la création, si le deuxième paramètre est manquant, on considère qu’il faut créer un motif vierge. Sinon, soit il s’agit d’un motif et on en fait alors une copie, soit il s’agit d’une liste de coordonnées et de numéros qui correspondent aux encoches à remplir.

Avant de continuer et de répondre aux questions du sujet, notez que l’affichage se fait par une méthode __str__ similaire à celle du tablier mais on remplaçant le numéro par le jeton de l’encoche :

class Motif:
    # ...
    def __str__(self):
        s = ''
        w, h = self.tablier.w, self.tablier.h
        width = len(str(self.to_num(w, h)))
        for y in range(h-1, -1, -1):
            s += f'{y} '
            for x in range(w):
                if self.inside(x, y):
                    s += f' {self.encoche(x, y).jeton():2}'
                else:
                    s += '   '
            s += '\n'
        s += f"  {' '.join(f'{x:{width}}' for x in range(w))}"
        return s

Exemple

Le motif présenté en section 1.2 Motifs du sujet pourrait se créer comme ceci :

>>> M0 = Motif(euro, [17, 18, 20, 29])
>>> print(M0)

6         ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ●  ○
2  ○  ●  ●  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Dans la suite, on encode un motif par un entier m qui est la somme de puissances de 2 par les numéros des encoches présentes dans le motif.

On peut alors rajouter une méthode encode à notre objet Encoche qui retourne la valeur 2^num qui se calcule aussi en décalant de num position vers la gauche l’entier 1 :

class Encoche:
    # ...
    def encode(self):
        return 1 << self.num

On peut donc ajouter une méthode num à un motif, qui retourne la somme des encodages des encoches pleines :

class Motif:
    # ...
    def num(self):
        return sum(encoche.encode() for encoche in self.encoches.values() if encoche.on())

L’exemple du sujet, section 1.2

>>> M0 = Motif(euro, [17, 18, 20, 29])
>>> M0.num()
538312704
>>> print(M0)

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ●  ○
2  ○  ●  ●  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Dans la suite, le sujet parle d’un type motif qui sera un entier (notre num) et d’un type ponctuel qui est un motif à une seule encoche.

Question 5

Elle demande d’écrire une fonction qui, pour un entier donné z numéro valide d’une encoche, retourne le motif ponctuel associé. Il s’agit simplement pour nous de construire un motif comme ceci :

>>> ponctuel = Motif(euro, [z])

def numero_vers_ponctuel(z):
    return 1 << z

let numero_vers_ponctuel z : ponctuel =
    1 lsl z;;

Question 6

Il s’agit cette fois de construire un motif de plusieurs encoches pleines :

>>> motif = Motif(euro, [z0, ... zn])

def numeros_vers_motif(l):
    return sum(1 << z for z in l)

let numeros_vers_motifs l : motif =
    List.fold_left
    (lor)
    0
    (List.map numero_vers_ponctuel l)
;;

Question 7

>>> motif_europeen = Motif(euro, euro.numeros())
>>> motif_europeen.num()
7950016668712476
>>> print(motif_europeen)

6        ●  ●  ●       
5     ●  ●  ●  ●  ●
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6

>>> MOTIF_EUROPEEN = numeros_vers_motif(NUMEROS_EUROPEENS)
>>> MOTIF_EUROPEEN
7950016668712476

let motif_europeen = numeros_vers_motifs numeros_europeens;;

Question 8

Le sujet demande de prouver la correction d’une fonction booléenne est_ponctuel qui retourne True ssi le motif passé en argument est ponctuel.

class Motif:
    # ...
    def est_ponctuel(self):
        m = self.num()
        return m > 0 and m & m-1 == 0

def est_ponctuel(m):
    return m > 0 and m & m-1 == 0

let est_ponctuel (m:motif) : bool =
    (m>0) && ((m land (m−1)) = 0) ;;

positions   :        j
m binaire   :   0..0 1 0..0
m-1 binaire : 0..0 0 1..1
m & m-1     :     0..0 0 0..0

positions   :        k      j
m binaire   :   .... 1 0..0 1 0..0
m-1 binaire : .... 1 0..0 0 1..1
m & m-1     :     .... 1 0..0 0 0..0

Question 9

La question porte sur l’écriture d’une fonction inclus qui prend en paramètre un motif m et un ponctuel p et qui retourne True ssi le ponctuel p est inclus dans m. On demande aussi une preuve de correction de la fonction.

>>> M = Motif(euro, [(3,5), (1, 1)])
>>> print(M)

6        ○  ○  ○       
5     ○  ○  ●  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ●  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> M2 = Motif(euro, M)
>>> M2.switch(38)
>>> print(M2)

6        ○  ○  ○
5     ○  ○  ●  ○  ○
4  ○  ○  ○  ○  ○  ○  ●
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ●  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> M2 > M
True
>>> M2.inclus(M)
True

def inclus(m, p):
    return m & p == p

let inclus (m:motif) (p:ponctuel) : bool =
    m land p <> 0
;;

Question 10

Il est temps de s’intéresser aux coups pour réaliser une partie c’est à dire passer d’un motif à un autre. Le but du jeu étant, en général de partir d’un motif initial pour atteindre un motif final (en un minimum de coups).

Cette question demande d’écrire une fonction qui, à partir d’un ponctuel p (qui, rappelons le, dans le sujet initial est un entier de la forme 2ⁱ où i est un numéro intérieur valide d’encoche) calcule le ponctuel obtenu par translation à gauche de l’encoche initiale. La fonction retourne 0 si jamais la translation fait sortir du tablier.

Dans le cas de la modélisation fonctionnelle (en Python comme en OCaml), la fonction voisin_g va se servir de la réponse à la question 4 (le voisin de gauche du numéro z vaut z-1) et du fait que passer de 2^z à 2^z-1 revient à faire un décalage à droite de 1.

La validité du voisin est réalisée par le test d’inclusion au motif plein.

def voisin_g(p):
    g = p >> 1
    return g if inclus(MOTIF_EUROPEEN, g) else 0

let valide (p:ponctuel) =
    inclus motif_europeen p;;

let voisin_g (p:ponctuel) : ponctuel =
    let res = p lsr 1 in
    if valide res then res
    else 0
;;

DIRECTIONS = {'N':(0,1), 'S':(0,-1), 'E':(1,0), 'W':(-1,0)}

class Motif:
    #...
    def voisin(self, direction, *args):
        new_motif = None
        direction = direction.upper()
        if direction in DIRECTIONS:
            x, y = args if len(args) == 2 else self.to_coords(args[0])
            dx, dy = DIRECTIONS[direction]
            nx, ny = x+dx, y+dy
            if self.on(x, y) and self.off(nx, ny):
                new_motif = Motif(self.tablier, self)
                new_motif.switch(x, y)
                new_motif.switch(nx, ny)
        return new_motif

class Motif:
    #...
    def inside(self, *args):
        x, y = args if len(args) == 2 else self.to_coords(args[0]) 
        return self.tablier.inside(x, y)

    def on(self, *args):
        return self.inside(*args) and self.encoche(*args).on()

    def off(self, *args):
        return self.inside(*args) and self.encoche(*args).off()

>>> M = Motif(euro, [(3,5), (1, 1)])
>>> print(M)

6        ○  ○  ○       
5     ○  ○  ●  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ●  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> M2 = M.voisin('E', 1, 1)
>>> print(M2)

6        ○  ○  ○       
5     ○  ○  ●  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ●  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> M3 = M2.voisin('N', 10)
>>> print(M3)

6        ○  ○  ○
5     ○  ○  ●  ○  ○
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ●  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Question 11

On cherche, à partir d’un motif m et d’un ponctuel p de ce motif, la liste des motifs atteignables ie les couples m’, p’ où p’ est la translation dans une des directions possibles du voisin de p dans cette direction et m’ le motif m privé de p mais auquel on a ajouté p’.

Dans sa modélisation fonctionnelle, l’algorithme du coup simple est le suivant :

• le ponctuel de départ doit faire partie du motif (sinon c’est qu’il n’y a pas de fiche et on ne peut donc pas faire de coups)
• on va calculer 2 étapes de voisins dans chacune des 4 directions
• un coup est effectif si aucun des voisins est nul (on ne sort pas du tablier) et si le premier voisin est inclus dans le motif (la fiche qu’on saute) et le second voisin ne l’est pas (emplacement libre)
• dès lors le nouveau motif est obtenu en :
  • supprimant le ponctuel de départ (par un ou exclusif entre le ponctuel et le motif) : on enlève la fiche de départ
  • supprimant le ponctuel correspondant au premier voisin : la fiche qu’on saute disparaît
  • ajoutant le ponctuel du second voisin (par un ou normal) : la fiche vient dans la nouvelle encoche

def coup_simple(m, p):
    coups = []
    if inclus(m, p):
        for voisin in (voisin_g, voisin_d, voisin_h, voisin_b):
            v = voisin(p)
            vv = voisin(v)
            if v and vv and inclus(m, v) and not inclus(m, vv):
                coups.append((((m ^ p) ^ v) | vv, vv))
    return coups

let coup_simple ((m,p) : motif∗ponctuel) =

    let coup voisin =
    (∗ Entrée : voisin, une des quatre fonctions voisin_g, voisin_d, voisin_h, voisin_b.
    Sortie : liste [ (m', p')] si le coup est possible, [] sinon ∗)
    let case_suivante = voisin p in
    let case_dapres = voisin case_suivante in
    if (inclus m case_suivante) && not (inclus m case_dapres) && case_dapres<>0 then [m−p−case_suivante+case_dapres, case_dapres]
    else []
    in
    List.flatten (List.map coup [voisin_g; voisin_d; voisin_h; voisin_b] )
;;

class Motif:
    # ...
    def simple(self, direction, x, y):
        motif = None
        dx, dy = DIRECTIONS[direction]
        voisin = x+dx, y+dy
        arrivee = x+2*dx, y+2*dy
        if self.on(*voisin) and self.off(*arrivee):            
            motif = Motif(self.tablier, self)
            motif.switch(x, y)
            motif.switch(*voisin)
            motif.switch(*arrivee)
        return motif, arrivee

class Motif:
    # ...
    def coup_simple(self, *args):
        coups = []
        if self.on(*args):
            x, y = self.to_coords(*args)
            for direction in DIRECTIONS:
                motif, arrivee = self.simple(direction, x, y)
                if motif is not None:
                    coups.append((motif, arrivee))
        return coups 

>>> M = Motif(euro, [28, 29, 37, 30])
>>> print(M)

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ●  ○
3  ○  ○  ○  ○  ●  ●  ●
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> coups = M.coup_simple(29)
>>> print(coups[0][0])

6        ○  ○  ○
5     ○  ○  ○  ○  ●
4  ○  ○  ○  ○  ○  ○  ○
3  ○  ○  ○  ○  ●  ○  ●
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> print(coups[1][0])

6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ○  ●  ○
3  ○  ○  ○  ●  ○  ○  ●
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Question 12

Cette question est l’extension de la précédente à une succession de déplacements simples. Partant d’un motif initial et d’un ponctuel (l’encoche qu’on souhaite faire bouger) on va mettre dans une file les motifs créés par coups simples à partir des motifs et des encoches arrivées retirés de la file.

Il s’agit donc d’un parcours en largeur des motifs accessibles depuis le motif initial. La version OCaml est récursive, la version Python itérative.

def coup_compose(m, p):
    coups = []
    if inclus(m, p):
        a_traiter = coup_simple(m, p)
        while a_traiter:
            coup = a_traiter.pop(0)
            coups.append(coup)
            for voisin in coup_simple(*coup):
                if voisin not in a_traiter and voisin not in coups:
                    a_traiter.append(voisin)        
    return coups

let coup_compose (c:motif∗ponctuel) =

    let rec aux l =
    if l=[] then []
    else
    let nv_couples = List.flatten (List.map coup_simple l) in
    nv_couples @ aux nv_couples

    in
    aux [c]
;;

class Motif:
    # ...
    def coup_compose(self, *args):
        coups = []
        if self.on(*args):
            a_traiter = self.coup_simple(*args)
            while a_traiter:
                coup, arrivee = a_traiter.pop(0)
                coups.append((coup, arrivee))
                for voisin in coup.coup_simple(*arrivee):
                    if voisin not in a_traiter and voisin not in coups:
                        a_traiter.append(voisin)        
        return coups

>>> M = Motif(euro, [17, 18, 20, 29, 36, 27])
>>> print(M)

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ○  ●  ○  ○
3  ○  ○  ○  ●  ○  ●  ○
2  ○  ●  ●  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

>>> coups = M.coup_compose(17)
>>> coups
[(<__main__.Motif at 0x25ba11c4160>, (3, 2)),
 (<__main__.Motif at 0x25ba11c4730>, (3, 4)),
 (<__main__.Motif at 0x25ba124a100>, (5, 2)),
 (<__main__.Motif at 0x25ba12645b0>, (5, 4)),
 (<__main__.Motif at 0x25ba1193f10>, (5, 4)),
 (<__main__.Motif at 0x25ba1195d00>, (5, 2)),
 (<__main__.Motif at 0x25ba1196430>, (3, 4)),
 (<__main__.Motif at 0x25ba11c4700>, (3, 2))]

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ●  ●  ○  ○
3  ○  ○  ○  ○  ○  ●  ○
2  ○  ○  ○  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

6        ○  ○  ○       
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ●  ○  ○  ○
3  ○  ○  ○  ●  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Question 13

Obtenir tous les coups jouables à partir d’un motif, en jouant n’importe quel fichet jouable. Les trois versions sont semblables :

class Motif:
    # ...
    def mouvements(self):
        return [m1 for (x, y) in self.encoches for (m1, _) in self.coup_compose(x, y)]

def mouvements(m):
    return [m1 for p in [numero_vers_ponctuel(z) for z in NUMEROS_EUROPEENS] for (m1, _) in coup_compose(m, p)]

let mouvements (m:motif) : motif list =

    let rec aux (p:ponctuel) =
    if p = 1 lsl 53 then []
    else (if inclus m p then coup_compose (m,p) else [] )
    @ aux (2∗p)
    in
    List.map fst (aux 4)
;;

Dans cette partie, la programmation OCaml ne sera plus fonctionnelle pure puisqu’une structure dictionnaire avec modification en place sera utilisée.

Le but des quatre dernières questions de cette première partie est de pouvoir calculer le nombre de coups minimum pour passer d’une configuration initiale m_i à une configuration finale m_f.

Nouvel Objet : Solitaire

Pour la version Python Objet, puisqu’on parle de partie, nous introduisons un nouvel objet Solitaire qui modélise une partie de solitaire sur tablier européen.

L’objet embarque donc un tablier, un motif initial, un motif final et une liste des motifs qui est la résolution du problème c’est-à-dire la succession de motifs partant du motif initial pour aller jusqu’au motif final en appliquant une série de coups simples.

La constante VIDE_43 représente l’ensemble de tous les numéros intérieurs sauf le 43 et PLEIN_35 représente le singleton {35}. La vidéo suivante : https://www.youtube.com/watch?v=5X2... montre qu’il existe une solution pour une configuration initiale avec un trou en 43 et une configuration d’arrivée avec un unique fichet en 35.

class Solitaire:

    def __init__(self, initial=VIDE_43, final=PLEIN_35):
        self.tablier = tb.Europeen()
        self.initial = Motif(self.tablier, initial)
        self.final = Motif(self.tablier, final)
        self.current_id = 0
        self.partie = [self.initial]
    
    def __str__(self):
        return self.partie[self.current_id].__str__()

    def goal(self):
        print(self.final)

>>> jeu = Solitaire()
>>> print(jeu)

6        ●  ●  ●
5     ●  ●  ○  ●  ●
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6

>>> jeu.goal()

6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ●  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Question 14

Mémoriser une entrée dans un dictionnaire, si cette dernière n’est pas encore présente et retourner True si le dictionnaire a été modifié. Nous présentons la méthode ajoutée à la classe Solitaire : la version Python fonctionnel n’est plus vraiment fonctionnel et identique.

class Solitaire:
    # ...
    def add_and_mem(self, dico, motif, s):
        num = motif.num()
        if num not in dico:
            dico[num] = s
            return True
        return False

let ajoute_et_pas_mem (d: dico) (s:int) (m:motif) =
    let dedans = Hashtbl.mem d m in
    if not dedans then Hashtbl.add d m s ;
    dedans
;;

Question 15

Il s’agit d’associer à un motif sa distance minimale au motif initial. Le principe est simple : si s est associé au motif m alors s+1 sera associé à tous les motifs atteignables depuis m par un coup composé (les motifs appartenant donc à m.mouvements()).

class Solitaire:
    # ...
    def strate(self, dico, s, motifs):
        ajoutes = []
        for m in motifs:
            for new_m in m.mouvements():
                if self.add_and_mem(dico, new_m, s):
                    ajoutes.append(new_m)
        return ajoutes

class Solitaire:
    # ...
    def strate(self, dico, s, motifs):
        return [new_m for m in motifs for new_m in m.mouvements() if self.add_and_mem(dico, new_m, s)]

let strate (d:dico) s (l:motif list) =
    let nv_motifs = List.flatten (List.map mouvements l) in

    let rec aux = function
    | [] −> []
    | m::suite when Hashtbl.mem d m −> aux suite
    | m::suite −> Hashtbl.add d m s; m :: aux suite
    in
    aux nv_motifs
;;

Question 16

On arrive à la fonction ultime : celle qui va parcourir le graphe des configurations jusqu’à atteindre la configuration finale. Dans la version objet les deux configurations sont des propriétés de notre objet Solitaire, la méthode partie minimale n’a donc pas d’autre paramètre.

class Solitaire:
    # ...
    def minimale(self):
        d_resultat = {}
        d_a_traiter = {self.initial.num():0}
        file_a_traiter = [self.initial]
        num_final = self.final.num()
        while num_final not in d_resultat and file_a_traiter:
            m = file_a_traiter.pop(0)
            num = m.num()
            s = d_a_traiter.pop(num)
            if num not in d_resultat:
                d_resultat[num] = s
            file_a_traiter.extend(self.strate(d_a_traiter, s+1, [m]))
        try:
            return d_resultat[num_final]
        except:
            KeyError('Motif final inatteignable')

let partie_minimale mi mf =
    let d = Hashtbl.create 42 in
    Hashtbl.add d mi 0 ;

    let rec aux sphere dist =
    (∗ sphere : ensemble des motifs à distance dist de mi. ∗)
    if Hashtbl.mem d mf then Hashtbl.find d mf
    else if sphere = [] then failwith "motif final non accessible"
    else
    let sphere_suivante = strate d (dist+1) sphere in
    aux sphere_suivante (dist+1)
    in
    aux [mi] 0
;;

Question 17

Telle quelle, non la fonction partie_minimale de l’énoncé ne répond pas à la question 1 : en effet rien n’est précisé sur la façon dont on ajoute les motifs dans la fonction strate. Hors, il est primordial de gérer les motifs par une file, ce qui est fait dans nos versions (on ajoute en fin de liste par un extend dans strate et on retire en tête par un pop(0)).

On considère la graphe dont les sommets sont les motifs et il y a un arc orienté d’un motif m₁ vers un motif m₂ si m₂ ∈ m₁.mouvements().

Voici un exemple :
M_i est la configuration initiale qui donne M₀, M₁, plus deux autres qui sont identiques par transposition et que nous n’avons pas représentées pour simplifier.

Puis de M₀ on atteint M₂ et de M₁ on atteint M_f la configuration finale. On constate donc qu’un parcours de ce graphe qui ne serait pas en largeur risque de passer par M₂ pour atteindre M_f et dès lors associer la distance 3. La distance minimale étant 2, en passant par M₁.

                                    Mi
                                  ○ ○ ○       
                                ● ● ○ ○ ○
                              ○ ● ● ○ ○ ○ ○
                              ○ ○ ○ ○ ○ ○ ○
                              ○ ○ ○ ○ ○ ○ ○
                                ○ ○ ○ ○ ○
                                  ○ ○ ○
                            /              \
                        M0                     M1
                      ○ ○ ○                  ○ ○ ○       
                    ○ ● ○ ○ ○              ● ○ ○ ○ ○
                  ○ ○ ● ○ ○ ○ ○          ○ ● ○ ○ ○ ○ ○
                  ○ ● ○ ○ ○ ○ ○          ○ ○ ● ○ ○ ○ ○      ...
                  ○ ○ ○ ○ ○ ○ ○          ○ ○ ○ ○ ○ ○ ○
                    ○ ○ ○ ○ ○              ○ ○ ○ ○ ○
                      ○ ○ ○                  ○ ○ ○
                        |                      |
                        M2                     Mf
                      ○ ○ ○                  ○ ○ ○       
                    ○ ○ ○ ○ ○              ○ ○ ○ ○ ○
                  ○ ○ ○ ○ ○ ○ ○          ○ ○ ○ ○ ○ ○ ○
                  ○ ● ● ○ ○ ○ ○    ->    ○ ○ ○ ● ○ ○ ○      ...
                  ○ ○ ○ ○ ○ ○ ○          ○ ○ ○ ○ ○ ○ ○
                    ○ ○ ○ ○ ○              ○ ○ ○ ○ ○
                      ○ ○ ○                  ○ ○ ○

Ce sujet bien construit autour du jeu du solitaire était intéressant. A noter que le jeu est très fortement combinatoire et il ne faut pas espérer pouvoir trouver le nombre de coups pour passer d’une vraie configuration initiale (en général où le tablier est complètement plein à part 1 encoche) vers une configuration finale constituée d’un unique fichet.

D’après Wikipédia :

Bien que le but affiché du jeu soit en général de démarrer avec un trou au centre du plateau pour finir avec un unique pion à la même place, cet objectif est impossible à atteindre avec le plateau européen. Hans Zantema en a fait une démonstration élégante qui tient en quelques lignes, basée sur la numérotation suivante du plateau de jeu avec les lettres A, B et C (une lettre par diagonale, en alternant les lettres) :

     A B C
   A B C A B
 A B C A B C A
 B C A B C A B
 C A B C A B C
   B C A B C
     A B C

Si on commence avec un trou au centre du plateau, alors il y a au début du jeu 12 positions A, 12 positions B et 12 positions C couvertes par des pions. On peut vérifier également qu’après chaque coup, le nombre de positions A couvertes augmente ou diminue de un, ce qui est vrai aussi pour le nombre de positions B et C. Donc après un nombre de coups pair, il y a un nombre pair de positions A couvertes, et de même pour les positions B et C ; et après un nombre de coups impair, il y a un nombre impair de positions A couvertes, et de même pour les positions B et C. Comme le plateau européen comporte 37 trous, après avoir retiré le pion central il faudrait 35 coups pour arriver à un seul pion, donc le nombre de positions A, B et C couvertes devrait être impair, ce qui impossible avec un seul pion. Le meilleur score atteignable dans cette configuration est de finir avec deux pions sur le plateau.

En fait sur un solitaire à 37 trous, il n’est possible de gagner que si le premier trou est dans l’une des cases marquées d’un X sur le diagramme suivant3 :

     X O X
   O O X O O
 X O O X O O X
 O X X O X X O
 X O O X O O X
   O O X O O
     X O X

Historique

L’origine du jeu du Solitaire reste floue. Il pourrait s’agir d’une évolution à un joueur du jeu médiéval Poules et Renard dont le support rappelle le tablier anglais à 33 trous et dont le système de prise en sautant est similaire.

Des références au jeu apparaissent fin 17^e dans la revue Mercure Galante, puis en 1710 dans le premier volume des Mémoires de l’Académie de Berlin par G.W. Leibniz. Edouard Lucas en fait le thème de sa cinquième récréation mathématiques en 1891 (p. 121-173). Il donne plusieurs théorèmes qui prouvent l’impossibilité de terminer avec un unique fichet si on commence avec un unique trou central. A noter la numérotation différente de celle du sujet des Mines :

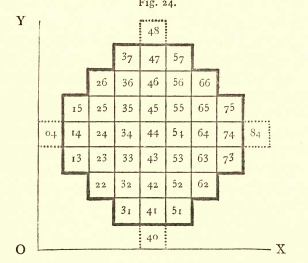
En 2009 le jeu fait le sujet d’un défi proposé en langage C et C++ par le site developpez.com. Un travail intéressant serait donc de compléter la classe Solitaire pour pouvoir résoudre un problème donné.

Script complet

Le script Python utilisé dans cet article est disponible ici :
Vous pouvez tester :

>>> jeu = Solitaire()
>>> jeu.minimale()

Qui va tenter de trouver le nombre de coups minimal pour passer de :

6        ●  ●  ●
5     ●  ●  ○  ●  ●
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6

à

6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ●  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

N’attendez pas d’obtenir la solution :). Lors de la résolution, le script affiche le nombre de motifs explorés.

Exemple de solution

Quelques méthodes ont été ajoutées pour pouvoir lire un fichier texte donnant sur la première lignes le numéro du trou pour la configuration initiale et celui de l’unique encoche pleine de la configuration finale puis la suite des mouvements pour y arriver. L’idée était d’avoir la partie décrite dans cette vidéo :

Vous pouvez tester la solution (dès lors la partie sera chargée dans la propriété partie et en faisant jeu.bk() et jeu.fd() vous pourrez naviguer) :

In [1]: %run solitaire
In [2]: jeu = Solitaire()
In [3]: jeu.load('solution.txt')

6        ●  ●  ●       
5     ●  ●  ○  ●  ●    
4  ●  ●  ●  ●  ●  ●  ● 
3  ●  ●  ●  ●  ●  ●  ● 
2  ●  ●  ●  ●  ●  ●  ● 
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
1/1
6        ●  ●  ●
5     ●  ●  ●  ○  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
2/2
6        ●  ●  ●
5     ●  ○  ○  ●  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
3/3
6        ●  ●  ●
5     ●  ●  ○  ●  ○
4  ●  ●  ○  ●  ●  ●  ●
3  ●  ●  ○  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
4/4
6        ●  ●  ●
5     ○  ○  ●  ●  ○
4  ●  ●  ○  ●  ●  ●  ●
3  ●  ●  ○  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
5/5
6        ●  ●  ●
5     ○  ●  ○  ○  ○
4  ●  ●  ○  ●  ●  ●  ●
3  ●  ●  ○  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
6/6
6        ○  ●  ●
5     ○  ○  ○  ○  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ○  ●  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
7/7
6        ○  ●  ●
5     ○  ○  ●  ○  ○
4  ●  ●  ●  ○  ●  ●  ●
3  ●  ●  ○  ○  ●  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
8/8
6        ○  ●  ●
5     ○  ○  ●  ●  ○
4  ●  ●  ●  ○  ○  ●  ●
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
9/9
6        ○  ○  ●
5     ○  ○  ○  ●  ○
4  ●  ●  ●  ●  ○  ●  ●
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
10/10
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
11/11
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ○  ○  ●  ●
2  ●  ●  ○  ●  ●  ●  ●
1     ●  ○  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
12/12
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ●  ●  ●  ●  ●  ●  ●
3  ●  ●  ●  ○  ●  ●  ●
2  ●  ●  ○  ●  ○  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
13/13
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ●  ●  ○  ●  ●  ●  ●
3  ●  ●  ○  ○  ●  ●  ●
2  ●  ●  ●  ●  ○  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
14/14
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ●  ●  ○  ●  ○  ●  ●
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
15/15
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ○  ●  ●
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
16/16
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ●  ●  ○  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
17/17
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ●  ○  ○  ●  ●
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
18/18
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ●  ○  ●  ○  ○
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
19/19
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ○  ○  ●  ○  ○
2  ●  ●  ○  ●  ●  ●  ●
1     ●  ●  ●  ○  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
20/20
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ●  ●  ○  ●  ○  ●  ●
1     ●  ●  ●  ●  ●
0        ●  ●  ●
   0  1  2  3  4  5  6
21/21
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ●  ●  ●  ●  ○  ●  ●
1     ●  ○  ●  ●  ●
0        ○  ●  ●
   0  1  2  3  4  5  6
22/22
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ●  ●  ●  ●  ●  ●  ●
1     ●  ○  ●  ○  ●
0        ○  ●  ○
   0  1  2  3  4  5  6
23/23
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ○  ○
2  ●  ○  ●  ●  ●  ●  ●
1     ○  ○  ●  ○  ●
0        ○  ●  ○
   0  1  2  3  4  5  6
24/24
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ●  ○
2  ●  ○  ●  ●  ●  ○  ●
1     ○  ○  ●  ○  ○
0        ○  ●  ○
   0  1  2  3  4  5  6
25/25
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ●  ○
2  ●  ○  ●  ○  ○  ●  ●
1     ○  ○  ●  ○  ○
0        ○  ●  ○
   0  1  2  3  4  5  6
26/26
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ●  ○
2  ●  ○  ●  ○  ●  ○  ○
1     ○  ○  ●  ○  ○
0        ○  ●  ○
   0  1  2  3  4  5  6
27/27
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ●  ○
2  ●  ●  ○  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6
28/28
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ●  ●  ●  ○  ○
3  ○  ●  ○  ○  ○  ●  ○
2  ○  ○  ●  ○  ●  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6
29/29
6        ○  ○  ○
5     ○  ○  ○  ○  ○
4  ○  ○  ○  ●  ○  ○  ○
3  ○  ○  ○  ○  ○  ○  ○
2  ○  ○  ○  ○  ○  ○  ○
1     ○  ○  ○  ○  ○
0        ○  ○  ○
   0  1  2  3  4  5  6

Une exploration plus profonde avec notamment l’utilisation d’une recherche en faisceau est proposée ici : Exploration du Solitaire