Dans cet article, on considère trois points $A$, $B$ et $C$ aléatoires, dont les espérances ont pour coordonnées respectives $\bar{A}\left(-\frac{3}{2} ;-\frac{1}{2}\right)$, $\bar{B}\left(\frac{5}{2} ;-\frac{1}{2}\right)$, et $\bar{C}\left(-\frac{1}{2} ;\frac{9}{2}\right)$.
Variables aléatoires
Aire
Le script Euler Math Toolbox suivant permet d’explorer la distribution des aires du triangle $ABC$ dans le cas gaussien :
(à condition d’avoir chargé le module de géométrie avec load geometry; au préalable).
Quelques explications sur les notations de ce script : Le symbole "underscore" représente la concaténation de matrices, la deuxième matrice étant placée sous la première. Le symbole "tube" fait la même chose mais en plaçant la deuxième matrice après la première (à droite). Enfin le symbole "prime" transpose les matrices.
Pour le cas uniforme, le script est le suivant :
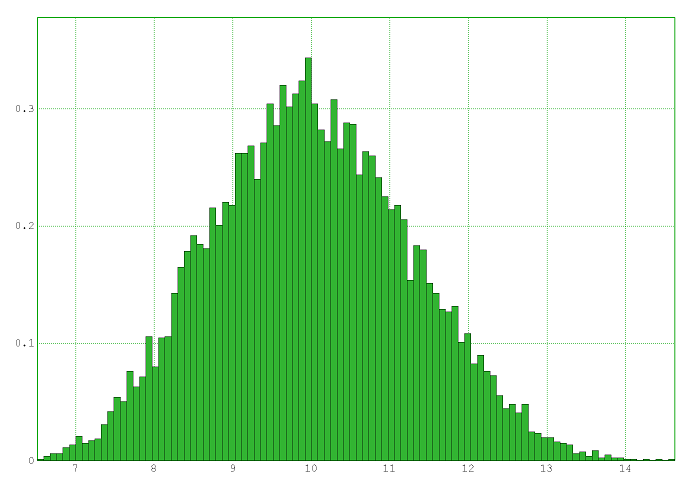
L’histogramme des aires ressemble alors à ceci :
Angles
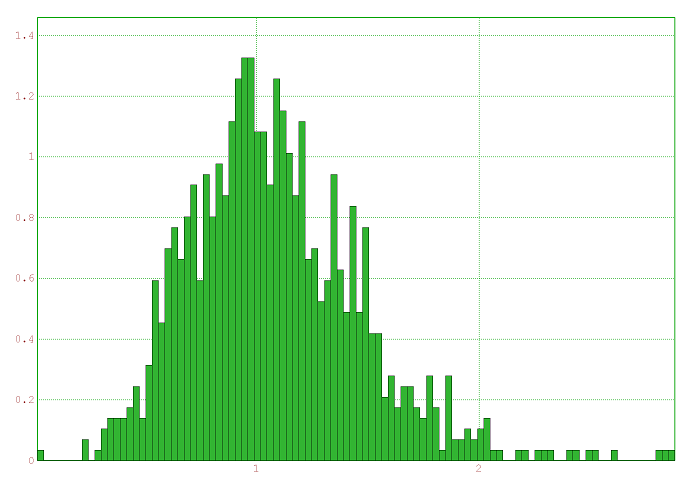
Même principe que ci-dessus, en remplaçant areaTriangle par computeAngle. L’histogramme des angles $\hat{A}$ ressemble à ceci,
dans le cas gaussien :
Et dans le cas uniforme :
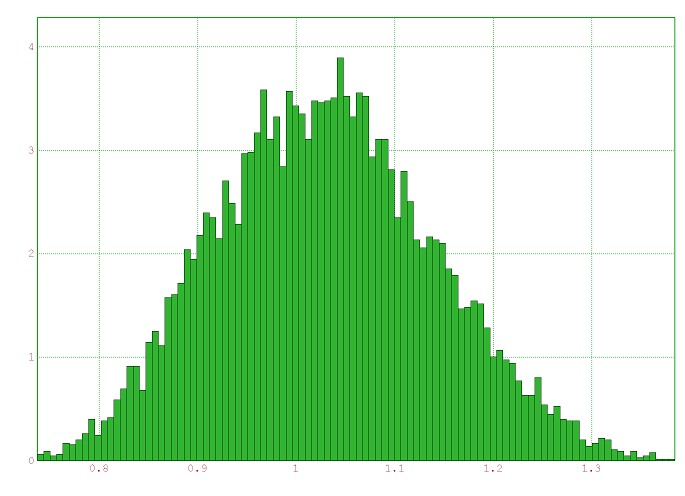
Il est bien sûr absolument impossible que cette distribution soit gaussienne (elle est bornée).
Rayon du cercle circonscrit
Même manip mais cette fois-ci avec getCircleRadius(circleThrough(A'[i],B'[i],C'[i])). Dans le cas uniforme, on obtient la courbe en cloche suivante :





Commentaires